网球以上旋球变向回击上旋球两种力学模式的生物力学分析
(河南科技大学体育学院 河南 洛阳 471000)
引言
网球运动中正手上旋击球是网球正手重要技术之一,对上旋球技术的研究自始至终是网球技术研究的主要课题。在关于上旋球研究方面,彭承基从动力学角度界定了网球的各种旋转球并分析了应对时动作要点;孙言铭等从运动学的角度对上旋球技术特征进行了分析;赵世壮等人研究了握拍法对上旋球击球效果的影响。本文不同于文献的运动学分析方法,本文在文献的弱上旋和强上旋定义基础上,提出“先正迎后正送”和“边侧迎边侧送”两种力学回击模式,力图为网球正手的强上旋技术的实践提供理论参考或理论依据。
1、网球强上旋球和弱上旋球及回击力来源与功能
1.1、网球强上旋球和弱上旋球
网球在空中运动中,随球心的平动与绕过质心轴的转动进行运动叠加,上旋球的自转角速度的方向指向平动方向左侧与平动方向呈右手螺旋,即图1中“离人而去”的方向,图1中V∥表示平动速度的水平分量。
对于半径为R,质量为m的网球,球面转动线速度是ωR。若ωR<
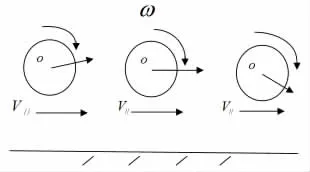
图1 上旋球示意图
1.2、回击力来源和各自功能分析
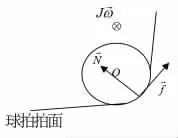
图2 回击力来源及功能分析用图
如图2所示,回击力是依靠弹力和摩擦力提供的。球和拍网碰撞引起球和拍子的网面形变从而产生弹力,其平均合力的方向与接触处的网面垂直并过球心,不产生相对质心的力矩,其功能是只改变球随质心的平动,不会直接性的影响球的转动,但弹力可以通过对摩擦力的影响间接性的影响球的转动。摩擦力沿着接触中心的切向,在影响球的平动与转动方面,由于摩擦力不过质心,其功能是既能够改变球的转动状态,也能够改变球的平动状态。
2、“边侧迎边侧送”和“先正迎后正送”上旋球变向回击力学模式
2.1、回击上旋球的一般力学动力方程
上旋球在空中运动是平动和向前转动两种运动的叠加。将上旋来球回击出上旋球,要求回击力必须具有两个作用效果,既能改变平动让球“有来有回”,又能改变转动让球“上旋来上旋回”。

图3 回击过程分析用图(俯视图)
2.2、“边侧迎边侧送”上旋球力学回击模式
根据(1)式,在来球和出球方向的分量关系为FcosβΔt=mV1(3a)式和Fcos(α-β)Δt=mV2(3b)式,根据前面回击力的来源和功能的分析,可知来自于回击过程中的弹力和摩擦力的合成,满足,其中的摩擦力按滑动摩擦考虑与弹力之间存在关系f=μN。力矩由摩擦力产生,满足 M=Rf,其沿着的投影满足 McosβΔt=0-Jω1(4a)式和 Mcos(α-β)Δt=Jω2-0(4b)式,这两式是(2)式分别在 J1方向和 J2方向的投影。
2.3、“先正迎后正送”上旋球力学回击模式
回到回击过程的平动的动力方程(1)式,可以运用矢量运算,按照 Δt1和 Δt2前后两个时间过程将其展开成,其中第一阶段的冲量1Δt1是Δt 的沿m1方向的分量与m1方向相反并且延长线过球心,第二阶段的冲量2Δt2是Δt 在 m2方向的分量与 m2方向相同并且延长线过球心,三者满足Δt=1Δt1+2Δt2。因为1Δt1与来球的转动平面垂直,2Δt2与出球的转动平面垂直,而且是先后在两个时间段Δt1和Δt2的回击作用力,因此把对应平动动力方程展开式的回击的力学模式称“先正迎后正送”。
3、两种模式各参量的约束关系及控制变量性分析
3.1、“边侧迎边侧送”中参量约束关系及分析
首先分析平动分运动。将“边侧迎边侧送”回击模式中的平分运动的动力学关系式 (3a)和 (3b)联立可得约束关系之一式,上式对于平均弹力相对地面有倾斜角度 θ 的情况也成立,只是根据及垂直于,F 的表达形式为F=Ncosθ-fsinθ。
另外联立“边侧迎边侧送”回击模式中上旋转动的(4a)和(4b)得到约束关系式,进而联立(7a)和(7b)得到第三个约束关系式。
控制变量性分析:第一,由(7a)式说明:在出球方向相对入球方向的角度变换α一定和作用冲量一定的情况下,若要提高出球速度V2,应加大β,即减小回击力方向与出球方向的夹角;第二,由(7b)式说明:在出球方向相对入球方向的角度变换α一定和作用力矩一定的情况下,若要提高出球角速度ω2,类似平动同样应加大β;以上这两点理论推导的结论是和网球动作技术要求相一致的。第三,(7c)式的约束关系说明入球和出球的上旋在相对强度时的相互转换,不能同强同弱。
3.2、“先正迎后正送”中参量约束关系及分析

图4 “先正迎后正送”回击模式分析用图
对应第一阶段的迎接过程,图示为图4:(a),其中θ1是弹力倾斜角。由(5a)式和(6a)式两个基本动力学关系结合弹力和摩擦力方向及功能,可以得到(N1cosθ1-f1sinθ1)Δt1= 和f1RΔt1=Jω1,然后联立这两式,再近似按照滑动摩擦讨论并引入关系 f1=μN1及整理后得到各参量约束关系,其中转动惯量J近似按照球壳计算,μ和n1是球与拍面之间滑动摩擦系数及入球的上旋强度。
对应第二阶段的迎接过程,图示为图4:(b)。由(5b)和(6b)两个基本动力学关系,可以得到 (N2cosθ2-f2sinθ2)Δt2=mV2和f2RΔt2=Jω2,进而得到约束关系。
控制变量性分析:由(8a)和(8b)两式说明,两个阶段约束关系一样且相互独立。前后两个阶段,弹力倾斜角都是限定条件满足tgθ</μ,满足此条件内在球面与拍面摩擦系数μ一定情况下,入球和出球上旋强度越大,弹力倾斜角越大,对应在动作技术上,意味击球时拍头越下垂。
4、总结
本文从等效性角度由力学基本定理定律分析提出了上旋球回击上旋球过程的两种力学模式 “边侧迎边侧送”和 “先正迎后正送”,进一步分析得到前者之中的两分运动相互约束,后者的是相互独立,各自具有控制变量性分析特点。因为本文采用的碰撞模型比较简单,而且没有对竖直方向分析,使得研究的结果具有近似性和特殊性,需要在以后的研究中进一步深化。

