桥梁结构涡激共振的敏感性
赵 林,刘丛菊,葛耀君
(同济大学 土木工程防灾国家重点试验室,上海 200092)
0 引 言
2020年4月26日至5月18日,武汉鹦鹉洲长江大桥、广东虎门大桥、浙江舟山西堠门跨海大桥接连突发大幅振动,引发社会舆论强烈关注。那么,究竟是什么原因造成的? 截至五月中旬,经专家组讨论已达成初步共识,即大幅振动的直接原因是来流导致的涡激共振。但舆论中仍然存在着许多其他观点——“系38#吊索钢丝绳断裂导致涡振[1]”。“38#吊索钢丝绳断裂”、“主缆腐蚀严重”等关键词迅速成为舆论热点。而事实上,虎门大桥已于2019年完成了38#吊索的更换,38#吊索并非是网传的大幅振动的罪魁祸首。
官方宣布了虎门大桥悬索桥5月5日大幅振动的主要原因:由于沿桥跨边护栏连续设置水马改变了钢箱梁的气动外形,在特定风环境条件下产生了桥梁涡振现象;后期持续涡振则与结构阻尼比明显下降有关。由此,人们了解到突发涡振并非是因为吊索损伤。但是仍有不少人心存疑惑。要说台风能把桥吹垮[2],很容易让人相信,小小的水马也会有这么大的影响? “涡振怕是借口吧,是因为当初结构设计有问题吧!”一时间,网络上各种质疑声不断涌现。
为何水马会导致桥梁产生涡振? 为何涡振会有如此大的威力? 本文主要尝试阐释这些疑惑。
1 涡激共振现象
节奏整齐的马蹄可以使一座便桥发生共振而断裂[3](图1),这是由于马蹄对桥梁产生很有节奏的作用力,当节奏频率接近桥梁固有频率时,发生共振,振动幅度不断增大,最终导致桥梁坍塌。桥梁在风的作用下也会产生类似的效果:风在通过桥梁时会形成旋涡,旋涡不断脱落时对桥梁施加有节奏的作用力,进而产生共振。

图1 桥的共振[3]Fig.1 Bridge resonance[3]
旋涡产生的原因与摩擦阻力有关。物体在平面上运动会存在摩擦阻力,风吹过物体也会受到物体提供的摩擦阻力。当风吹过物体表面时,在摩擦阻力的影响下,风速不断减小,这使得物体表面压力增大,摩擦阻力也随着增大,继而导致在摩擦阻力的影响下风速进一步降低。图2所示是一簇自左向右的风,由于物体表面存在摩擦阻力,靠近物体表面的风速不断减小。同时由于空气中的分子之间存在相互作用力,也就是黏性力,上层的风受到下层风的影响,速度减小,同时风向发生改变。当初始风速与黏性力大小满足一定关系时,从物体尾部脱离的风就变成了旋涡的形态。
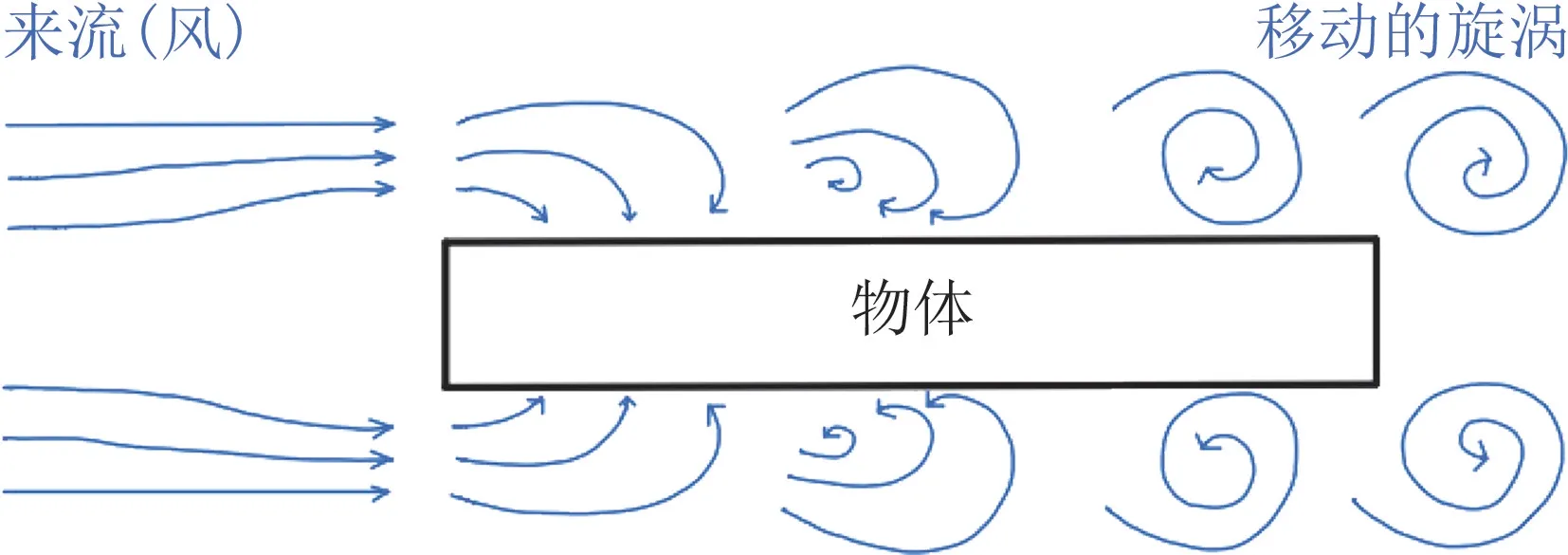
图2 旋涡形成过程示意图Fig.2 Schematic diagram of vortex generation
风在物体两侧尾部形成旋涡,当风速较小或黏性力较大时,两侧形成的旋涡较小,呈对称分布,如图3所示。当风速增大或黏性力减小时,形成的旋涡将逐渐增大。接下来将发生什么现象? 1911 年,科学家冯·卡门和希门茨通过试验发现,风绕经结构体后会形成交替排列、旋转方向相对的成对旋涡。为了纪念这一发现,将其称为卡门涡街,如图3、图4所示。图5为宽高比为1∶5的矩形在流场中产生的不同运动相位处的旋涡绕流图[4]。引入无量纲参数雷诺数(Re),雷诺数反映了来流空气微团的惯性力与黏性力之比,对旋涡脱落频率有着显著影响。
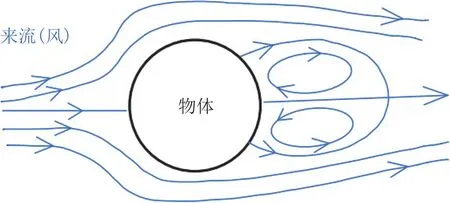
图3 对称旋涡脱落[5]Fig.3 Symmetric vortex shedding[5]

图4 圆柱卡门涡街[5]Fig.4 Cylindrical von Karman vortex street[5]
总体上看,风绕经物体后产生了旋涡。当出现卡门涡街时,旋涡交替脱落会形成周期性的涡脱力作用在物体上。当涡脱力频率接近于桥梁结构的某一固有频率,桥梁结构发生大幅振动,这一现象就是涡激共振,简称涡振。就像变形状态的蹦床会给它上面的物体施加一定的力一样,振动状态下的桥梁结构对旋涡会施加一定的反作用力。从而,在气弹效应(桥梁运动与气流之间的相互作用)的反馈作用下,涡脱力频率只需稍微接近桥梁结构的某一固有频率,就会发生特定风速范围的双向共振效应,这种现象称为锁定现象。即,在一段范围内的风速都会使桥梁产生大幅振动,引发涡激共振。由此,桥梁结构此时所受的涡激力为在原有周期性涡脱力的基础上附加了与桥梁运动有关的自激力项[6]。
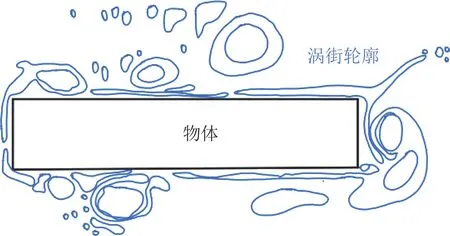
图5 矩形旋涡绕流图[4]Fig.5 Vortex flow pass rectangular[4]
我们也可以进行一个小试验,演示卡门涡街的产生。试验前准备好以下物品:(1)一个直径0.04 m左右的圆柱体,如固体胶棒、擀面杖等;(2)一张长度大于0.20 m 的纸条;(3)一个可以变档的电吹风机。
将小纸条一端粘附在圆柱体上,如图6所示,用电吹风机从上向下吹。其中有一定直径的圆柱体可以引发旋涡的产生。由于纸条受重力作用静止时方向向下,所以从上向下吹可以更方便地控制风向与纸条方向一致。调整电吹风机的档位与风向,当调到合适位置时将观察到,由于圆柱体后侧即纸条位置处存在交替脱落的旋涡,纸条抖动明显增大,这时产生的就是卡门涡街[7]。纸条在旋涡周期性脱落施加的力的作用下产生涡振。如若未观察到,可尝试以下解决方法:(1)替换更柔软的纸条;(2)增加纸条长度;(3)增大圆柱体直径。
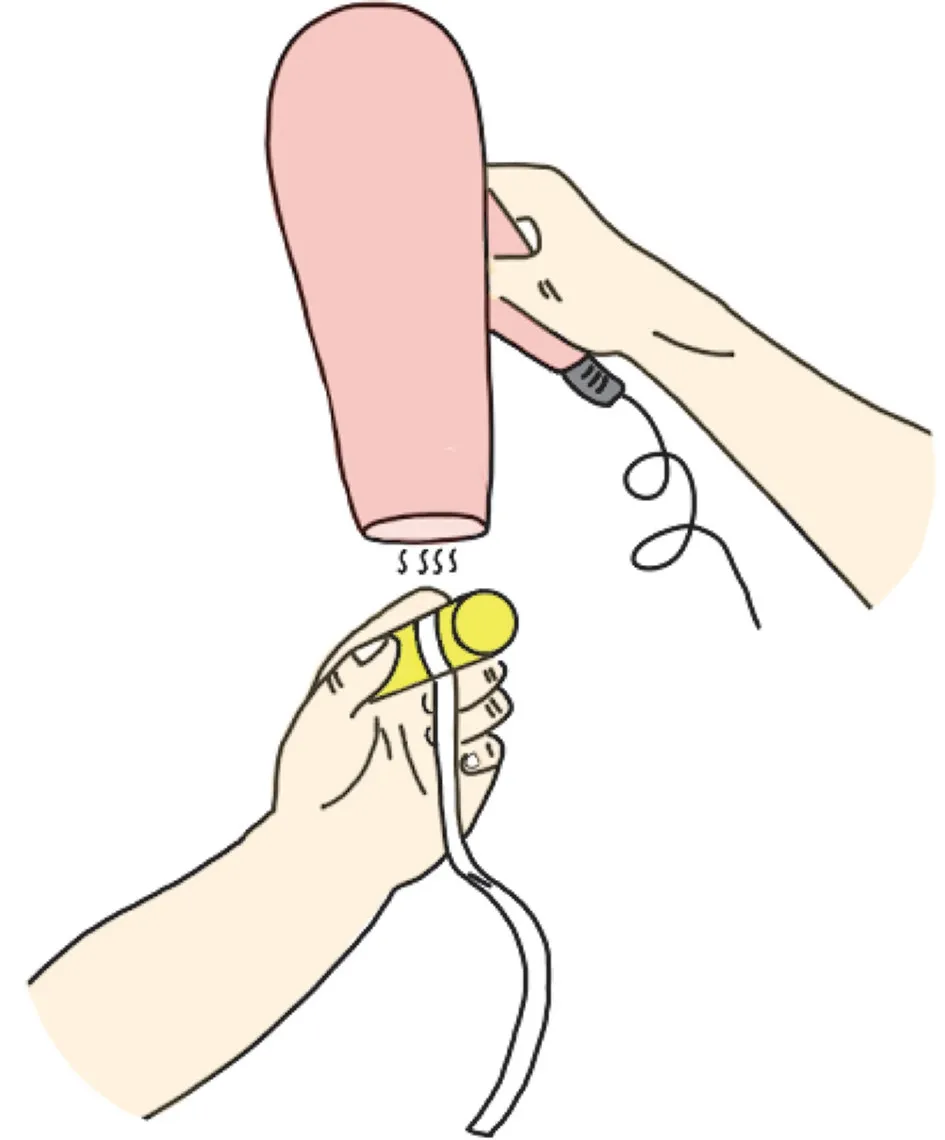
图6 风吹粘附在圆柱体上的纸带试验示意图Fig.6 Schematic diagram of wind-blown paper tape adhered to cylinder
如果说任何一座桥在风的作用下本质上均会发生涡振,听起来是否会觉得有些可怕? 其实不只是桥梁,很多生活中的物品在风环绕流过时都会产生涡振。比如,微风下规律振动的晾衣杆、随风飘扬的国旗等,这些都是受到了涡振的影响,只是因为大多数情况下产生的影响不大所以很容易被人们忽略。
因此,对于桥梁涡振无需过分担心。一方面是因为仅在风速满足一定的条件下才可能发生,且发生需要满足涡脱力频率接近于桥梁结构的某一固有频率,否则振动幅度是可忽略的。另一方面是因为,即使存在锁定现象扩大了风速范围,但由于结构本身存在一定的抵抗能力,即结构的阻尼效应,可以不断消耗外界周期性激励,保证了结构振动的幅度是有限的。当然,最重要的是,正规的工程建设施工前都经过了科学的设计和验算,并且越来越多的抑振措施已经被应用在涡振控制中,还有桥梁健康监测系统和桥梁运营维护单位定期的年检作为保障。而这次虎门大桥产生涡振的原因只是由于临时增铺了相当长度的水马,造成了桥梁外形结构非设计状态的改变。
不过大家可能仍然感到好奇,经过验算的桥,仅仅增加水马就能有这么大影响吗? 这就要从涡振对外形的敏感性说起了。
2 涡振对外形尺寸的敏感性
为保证悬索桥在减轻重量的同时不易发生变形,通常采用钢箱梁截面。虎门大桥就是典型的钢箱梁悬索桥。虎门大桥桥梁横截面包括钢箱梁梁体与桥面上方两排栏杆、中央隔离带与梁底四排检修车轨道等结构附属构件(参见图7)。

图7 虎门大桥横断面简图[8]Fig.7 Simplified cross section of Humen Bridge[8]
针对此次虎门大桥大幅振动事件,采用数值模拟方法计算主梁增加水马后的旋涡脱落情况,并与在栏杆上增加抑流板的结果进行对比。由图8可以明显看出,在有水马时,桥梁上下表面存在明显的周期性旋涡脱落,由交替性的气动激励效应而产生涡振;而增加抑流板并撤除水马后,抑流板的存在会显著破坏原周期性大尺度旋涡的生成,上表面有规律的旋涡显著消减,可以从根源上减弱和避免涡振的发生[9-10]。
除了水马,能引起附加旋涡并导致涡振的潜在结构附属构件还有哪些? 答案是图8中所有挡在风前进方向上的结构附属构件都会潜在引起涡振,这类结构可以统称为“钝体”。桥梁的主梁是钝体,检修车轨道是钝体,两侧的栏杆也是钝体,甚至虎门大桥上52 mm直径的吊索也是钝体。而涡振的一个重要特征是对结构外形非常敏感,结构外形直接决定了气流遇到断面后的分离和形成旋涡的特点,对涡振的发生及振幅大小至关重要。大到桥梁断面的形式、检修车轨道位置,小到栏杆形状、拉索粗糙度的改变,结构外形微小的改变都会对涡振带来影响。但由于桥梁断面和附属构件的多样性,附属构件对桥梁断面涡振性能的影响尚未形成统一认识。目前多采用试验的方式选择最为合适的附属构件外形及位置,从而改善整个桥梁断面气动外形,降低结构的涡振风险[11]。
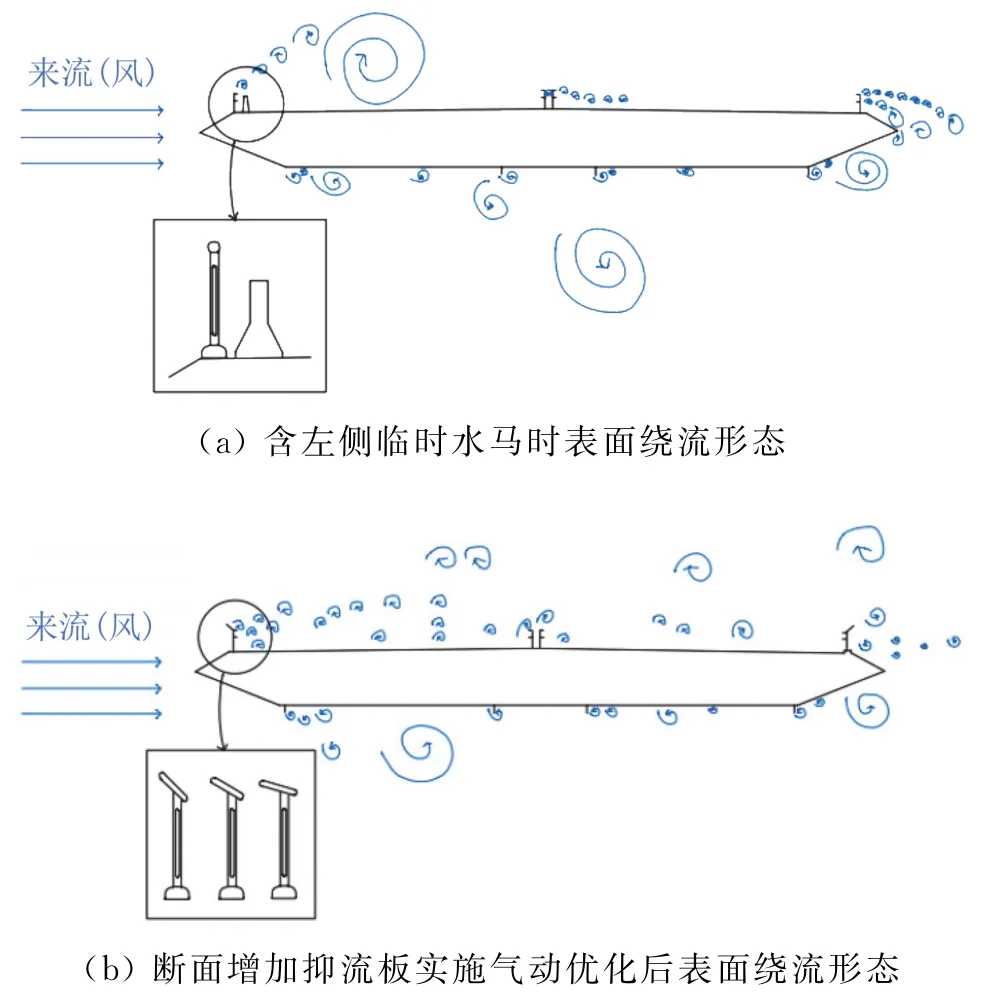
图8 虎门大桥主梁表面绕流示意图[10]Fig.8 Schematic diagram of surface flow around girder of Humen Bridge[10]
在研究涡振时,为了使结构尺寸改变量更加直观,一般将构件尺寸与大跨桥梁主跨梁高进行对比(本文取梁高为4.0 m),取其比值进行描述。以前文的水马为例,水马高度0.8 m,桥梁梁高4.0 m,即增设的水马高度为桥梁主跨梁高的1/5。下面简单讨论不同结构尺寸改变量下的涡振敏感性。
2.1 1/5左右的结构尺寸改变量
1/5左右的结构尺寸改变量,即,结构尺寸的改变量约为桥梁主跨梁高的1/5。一般的桥梁设计中,为了定期对桥梁进行监测与维修,通常在梁底安装检修轨道。以南京长江第四大桥为例[12],检修轨道安装在斜腹板和底板交界的区域。由于此区域为梁底气流的分离区域,因此不同轨道位置对涡振会产生显著影响。当检修轨道距梁底转角点距离由800 mm增大到4800 mm 时(图9b),涡振振幅减小到原来的1/20,而此时结构的改变量仅约为桥梁主跨梁高的1/5。如果采用加装检修轨道导流板的方式(图9c),涡振振幅则可减小到原来的1/4。检修轨道位置示意图和涡振响应图见图9和图10。我们注意到,南京长江第四大桥原设计方案在2~3 m/s、4~5 m/s风速条件下存在两个涡振锁定区间,涡振最大单幅响应达到100 mm 和180 mm。
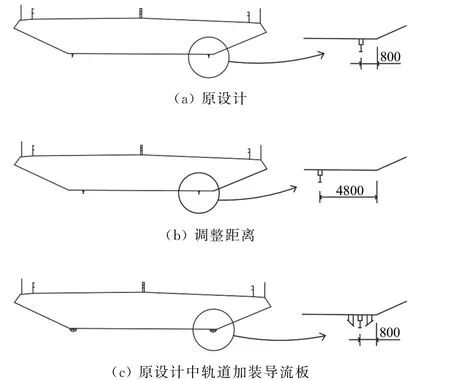
图9 不同检修车轨道方案(单位:mm)[12]Fig.9 Maintenance rail schemes(unit:mm)[12]
桥梁设计时通常会在桥面栏杆上方安装抑流板,用来影响旋涡脱落的位置,减小涡激力的大小,以抑制涡振。一般栏杆高度约为1.1 m,在栏杆上安装10°仰角、高度为0.8倍栏杆高度的抑流板后(图11),涡振振幅减少16%。当抑流板的高度增加到栏杆高度的1.2倍时,振幅则可减小50%[13]。
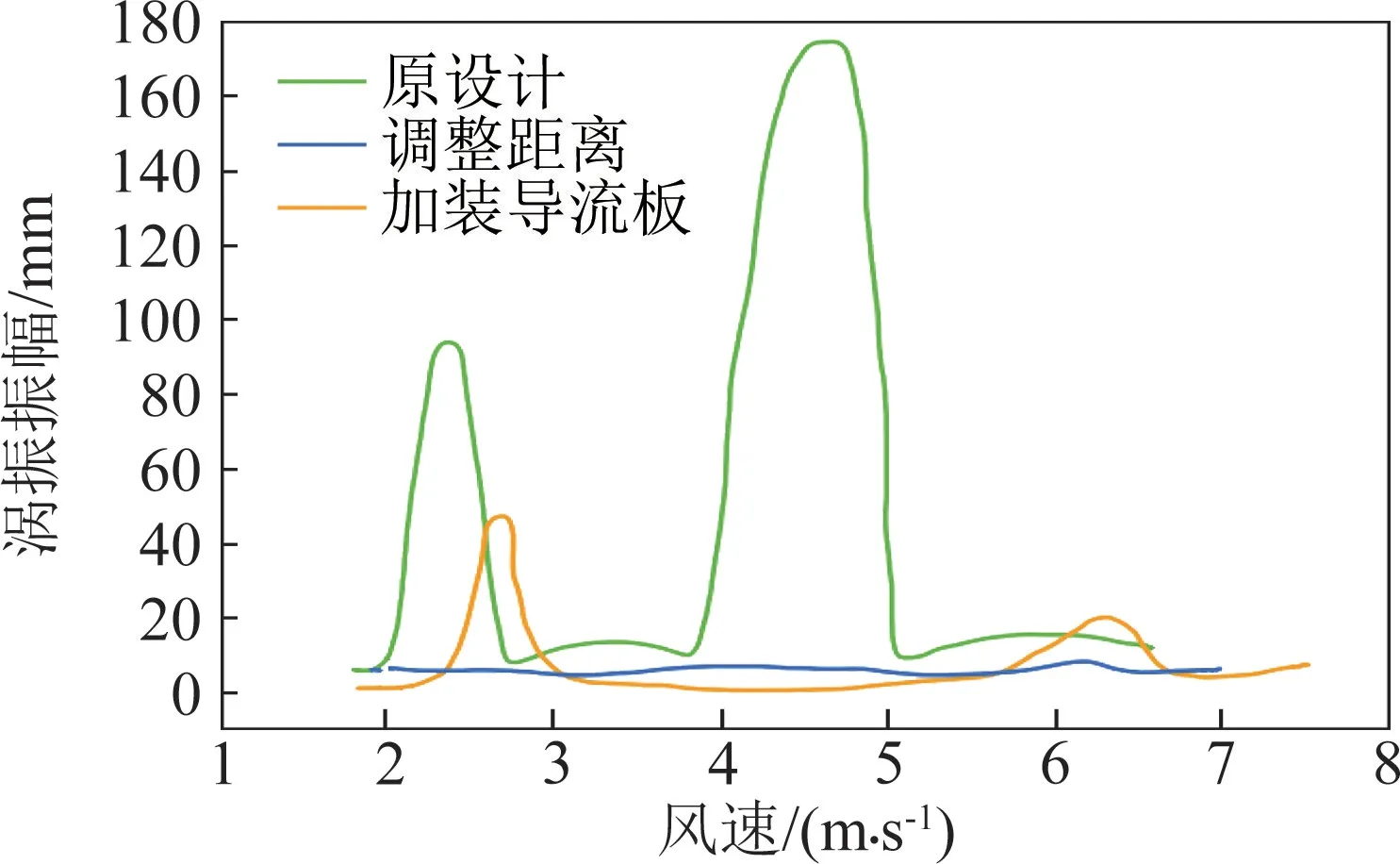
图10 不同检修车轨道方案对涡振振幅影响[12]Fig.10 Influence on vortex-induced vibration amplitude of various maintenance rail schemes[12]
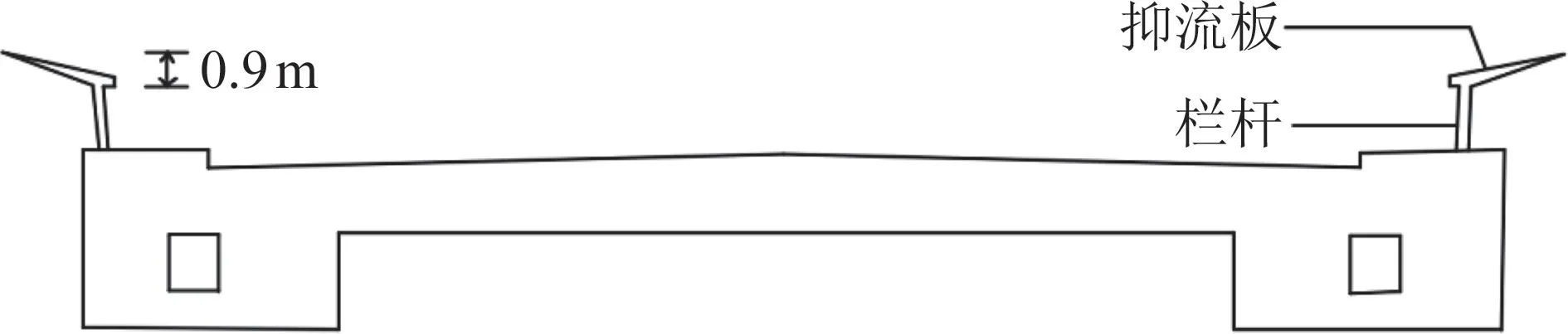
图11 增加抑流板桥梁断面图[13]Fig.11 Cross section of bridge with additional spoilers[13]
2.2 1/50左右的结构尺寸改变量
栏杆截面尺寸的改变量一般约为桥梁主跨梁高的1/50至1/100量级。在这个量级下,圆截面栏杆和方截面栏杆,哪种抑制涡振的效果更好? 答案是圆截面栏杆(图12a)。在采用边长119 mm 方截面栏杆时,出现明显的涡振,而采用直径为119 mm 的圆截面栏杆则无明显涡振现象(参见图13)[14]。由此可见,即使是这种小尺度的改变量,也能对整桥的涡振产生巨大影响,所以涡振对于结构尺寸是相当敏感的。
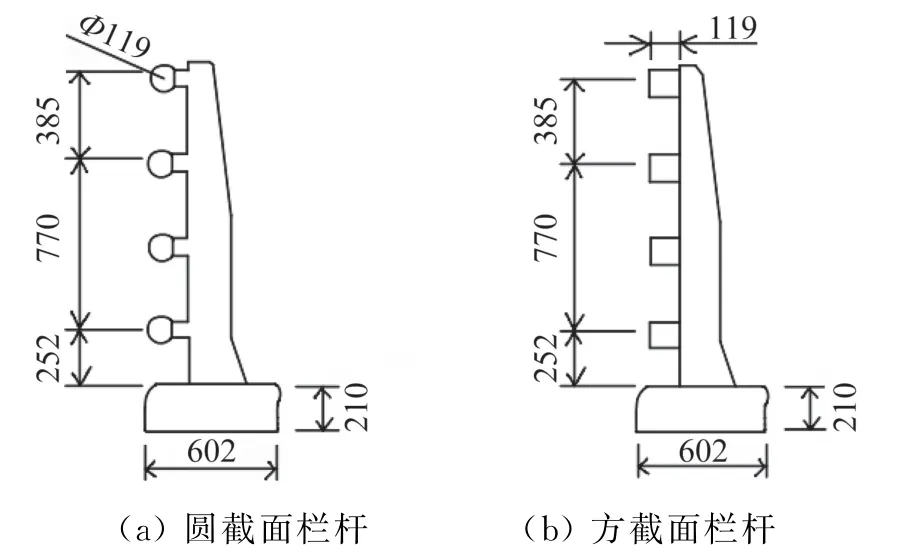
图12 栏杆外形及尺寸(单位:mm)[14]Fig.12 Configuration and size of barriers(unit:mm)[14]
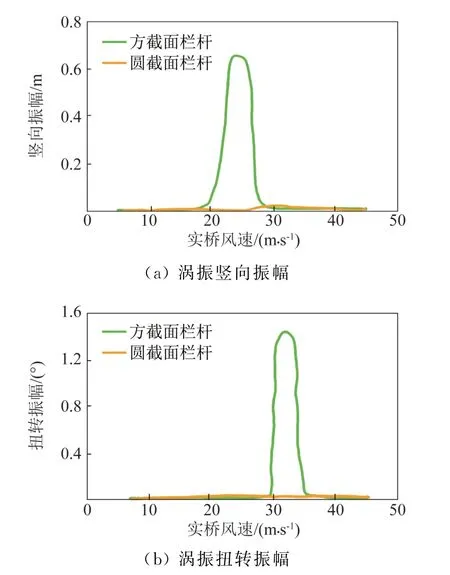
图13 不同栏杆形式下的振幅[14]Fig.13 Amplitude under different barrier forms[14]
2.3 更细微的结构尺寸改变量
其实,存在超出想象的事实,相对于大跨桥梁的巨大长度、宽度及高度尺寸,拉索的表面粗糙度、表面涂层材料、设置的螺旋线及凹坑这些表面状态的细微改变,都会对涡振产生影响。举例来说,直径为70 mm的斜拉桥拉索,改变表面粗糙度对涡振的影响究竟能有多大呢? 通过对拉索模型进行试验研究发现,对于表面采用均匀等效砂砾模拟粗糙壁面的拉索,当布置高度hs=0.7 mm 的均匀等效砂砾时(图14),作用在拉索上的涡激力大幅减小,拉索振幅最大可减少84.4%[15]。而在拉索表面设置1.5 mm 高度的螺旋线(图15),则能完全抑制拉索大幅振动[16]。
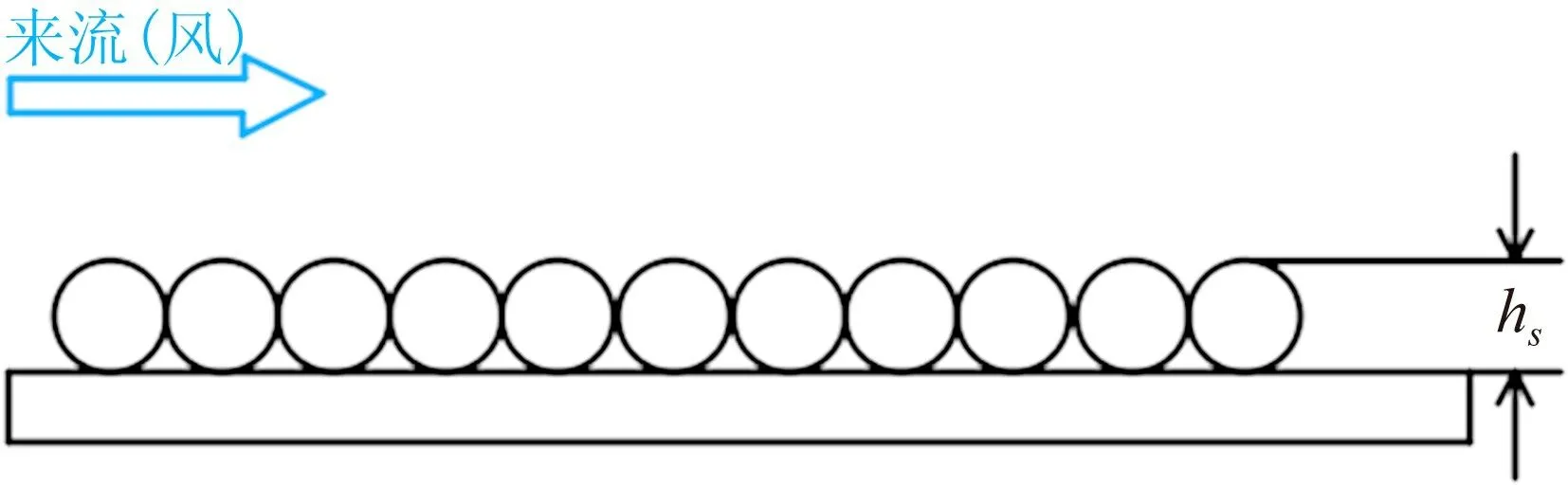
图14 等效砂砾粗糙度模型[15]Fig.14 Equivalent gravel roughness model[15]

图15 拉索粗糙度模型[16]Fig.15 Model of stayed cable roughness[16]
在与涡振类似的风雨激振过程中,已有试验数据表明,使用聚脲涂层(一种高效的防腐耐磨材料)改变斜拉桥拉索表面的憎水性可以增加水线的摩擦力,使得水线难以在惯性力和风压的作用下发生振动,通过使水线形态发生改变进而实现抑制风雨激振振幅的效果[16]。在进一步的试验中发现,聚脲涂层的采用可以改善拉索的顺风向载荷,在一定雷诺数区域内,其阻力系数CD较无表面处理拉索要低(参见图16);但同时与横风向风载荷有关的升力系数CL却在一定范围内增加(参见图17),导致了拉索的不稳定性。虽然有关涂层对涡振产生的影响有待研究,但是以上试验足以说明,类似于表面状态这种细微的结构尺寸改变也能对结构气动绕流产生很大影响[17]。
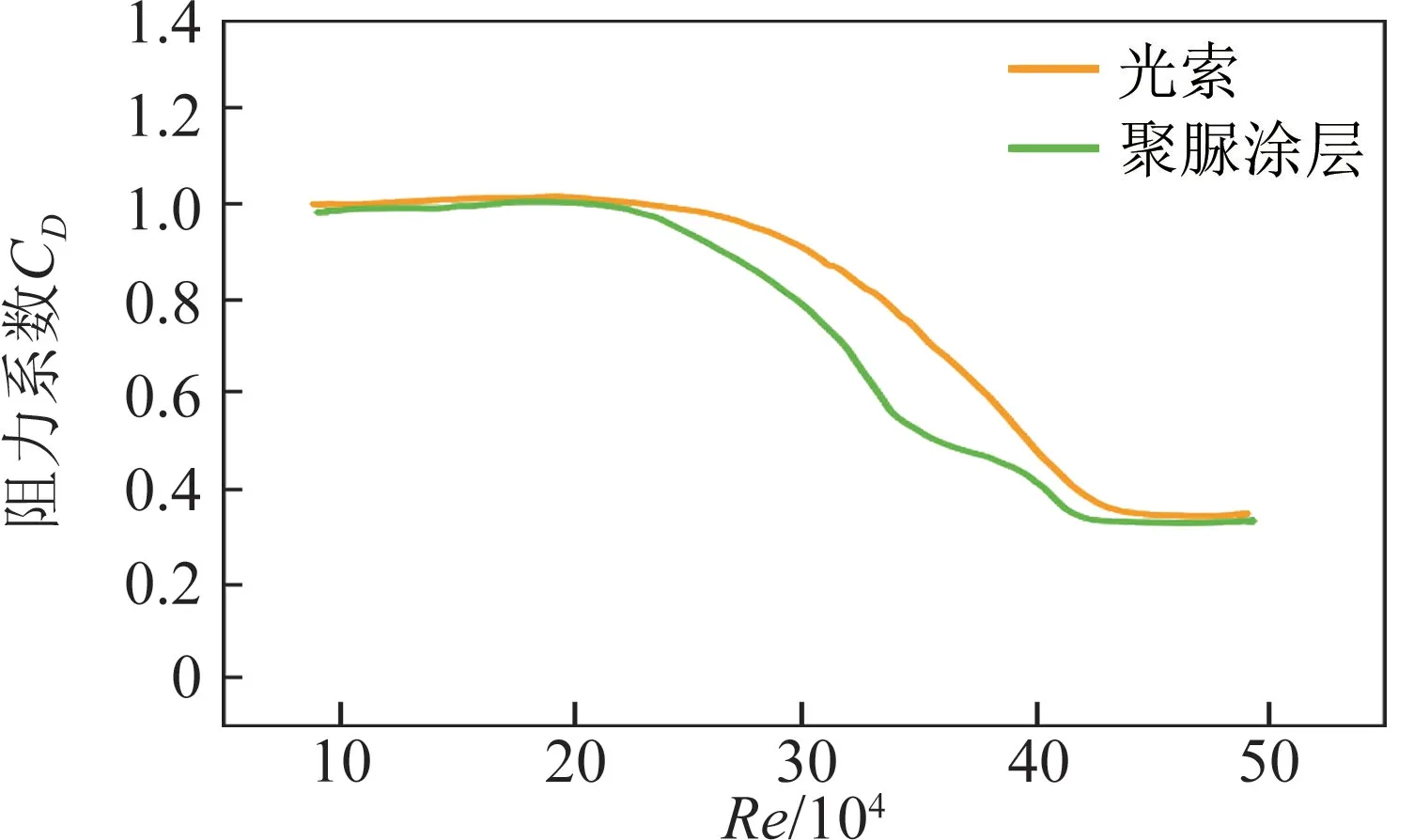
图16 阻力系数随雷诺数变化规律[17]Fig.16 Variation law of drag coefficient vs.Reynolds number[17]
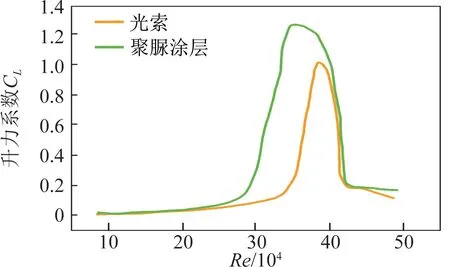
图17 升力系数随雷诺数变化规律[17]Fig.17 Variation law of lift coefficient vs.Reynolds number[17]
上面讨论的仅仅是单根拉索的情况。那么这么细的拉索会对桥梁整体涡振振幅产生很大的影响吗?在对苏通大桥的静风响应分析中发现,桥面上所有斜拉索横向风载荷引起的位移在总体中所占比例超过40%[18]。因此,虽然目前拉索的影响在桥梁涡振响应振幅中的具体比例还有待进一步研究,但仍可以初步判断其影响是显著的。
2.4 桥面行车对涡振的影响
在桥面上行驶的汽车是否也会改变桥梁外形进而影响涡振? 答案是肯定的。无车状态的桥梁涡振振幅是有车状态的3倍。简单来看,一方面车辆的存在扰乱了旋涡,对涡振的抑制产生有利影响;另一方面,车辆使得桥梁的重量增加,使得振动更加困难。不仅如此,实际上在交通量比较大的情况下,车辆的存在在一定程度上改变了桥梁原有外形的规则分布,也相当于改变了主梁表面的粗糙度。而试验研究证明,涡振振幅随桥面粗糙度的增加是不断减少的。在用砂纸模拟粗糙度的试验中,将80目砂纸贴于桥面时的涡振振幅是光滑桥面振幅的1/4[19-20]。所以总体来看,桥面行车有利于抑制涡振振幅。
顺便说一下,大跨度桥梁在长期的运营中,由于各种载荷作用导致桥面出现一定量的粗糙度,从而对桥梁的涡振性能也产生一定的影响。以此类推,0.8 m 高的水马能产生这么大的涡振影响效果,就不难理解了。
3 涡振对阻尼比的敏感性
坐秋千时,需要不断施加推力以保持稳定的运动,主要是因为结构阻尼在不断消耗动能。阻尼是指结构振动过程中,系统本身固有的摩擦能耗机制引起的能量逐渐衰减,进而使振动幅度逐渐下降的特性。同时,相同大小的阻尼力对不同大小结构的影响也会不同。为了更加具体地表现阻尼的相对大小,引入了无量纲数阻尼比ξ。涡激力可以理解为是在不断推动桥梁运动的“手”,给桥做功。当涡激力所做的功大于桥梁阻尼消耗的能量时,这部分多出来的功转化为桥梁的动能,振动幅度会越来越大,反之则振幅越来越小。因此,涡振对阻尼比也非常敏感,通常结构阻尼比增大,振幅更易衰减。在东海大桥港桥连接段——颗珠山大桥的节段模型试验中,9.1‰阻尼比下的最大扭转振幅仅为5.1‰阻尼比时的1/10,同时振动的风速区间也相应地减小(参见图18)[21]。
那么桥梁的阻尼比是如何产生的? 对于桥梁结构而言,结构本身所具有的阻尼及周围介质提供的阻尼是两类主要的阻尼组成部分,前者主要取决于结构类型、材料、构筑方式及各部件之间的连接方式,而周围介质提供的阻尼主要是桥梁墩台及台后填土提供的约束阻尼、摩擦耗能等[22]。由于桥梁结构的长期使用,桥梁内部会产生疲劳裂缝,当桥梁在载荷作用下产生振动时,裂缝界面的张开/闭合产生的摩擦耗能是结构阻尼比的主要来源。在钢筋混凝土梁上分级加载载荷,每增加一次载荷看作梁的损伤增加一级,即裂缝数量增多、宽度增加。通过观察不同等级载荷下阻尼比与时间的变化曲线可以发现,整体上阻尼比随载荷等级的增加呈现先增加后减小的趋势(参见图19)。这是因为从完好状态到第3级损伤状态,梁内裂缝数量增加将增强结构的耗能性能,进而阻尼比也增大。之后增加载荷,虽然裂缝数量仍在增加,但由于裂缝宽度的增大,裂缝闭合性降低导致单个裂缝耗能减少,二者对阻尼比的影响抵消,阻尼比保持不变[23]。同时从图19可以看出,不同载荷下的结构阻尼比均随时间呈现递减趋势。那么,前文提到的虎门大桥后期持续涡振与结构阻尼比明显下降有关,就很容易理解了。那么我们大胆地猜测一下,如果长期观测桥梁的阻尼比,数据会呈现怎样的变化趋势? 通过黄石长江大桥、钱塘江三桥、汕头海湾大桥的阻尼比多年监测数据发现,阻尼比随时间呈现先微幅上升然后持续下降的趋势(图20)[24]。
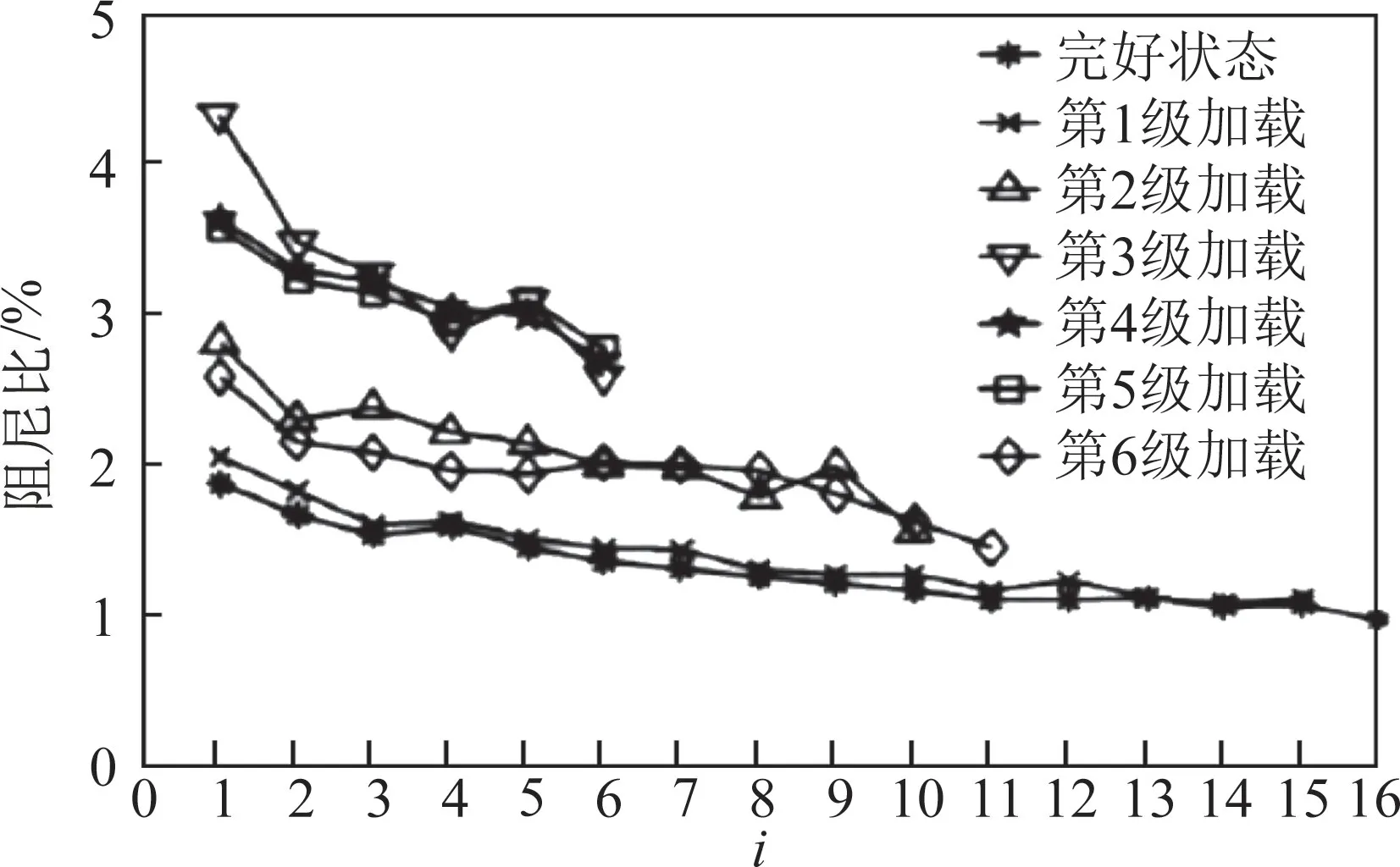
图19 阻尼比与加载载荷[23]Fig.19 Damping ratio and load[23]
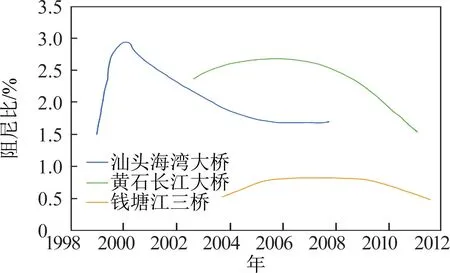
图20 桥梁阻尼比随时间演变示意图Fig.20 Schematic diagram of bridge damping ratio evolution with time
同时,空气温度、空气湿度、太阳辐射强度等环境因素均会影响结构阻尼比[25]。在同济大学风工程研究团队对浙江舟山西堠门跨海大桥的长年观测中,得到了如图21所示的的阻尼比变化曲线。数据显示,在每年四五月份,阻尼比会普遍较低。看来近来几座大桥接连发生涡振也是“有迹可循”的。
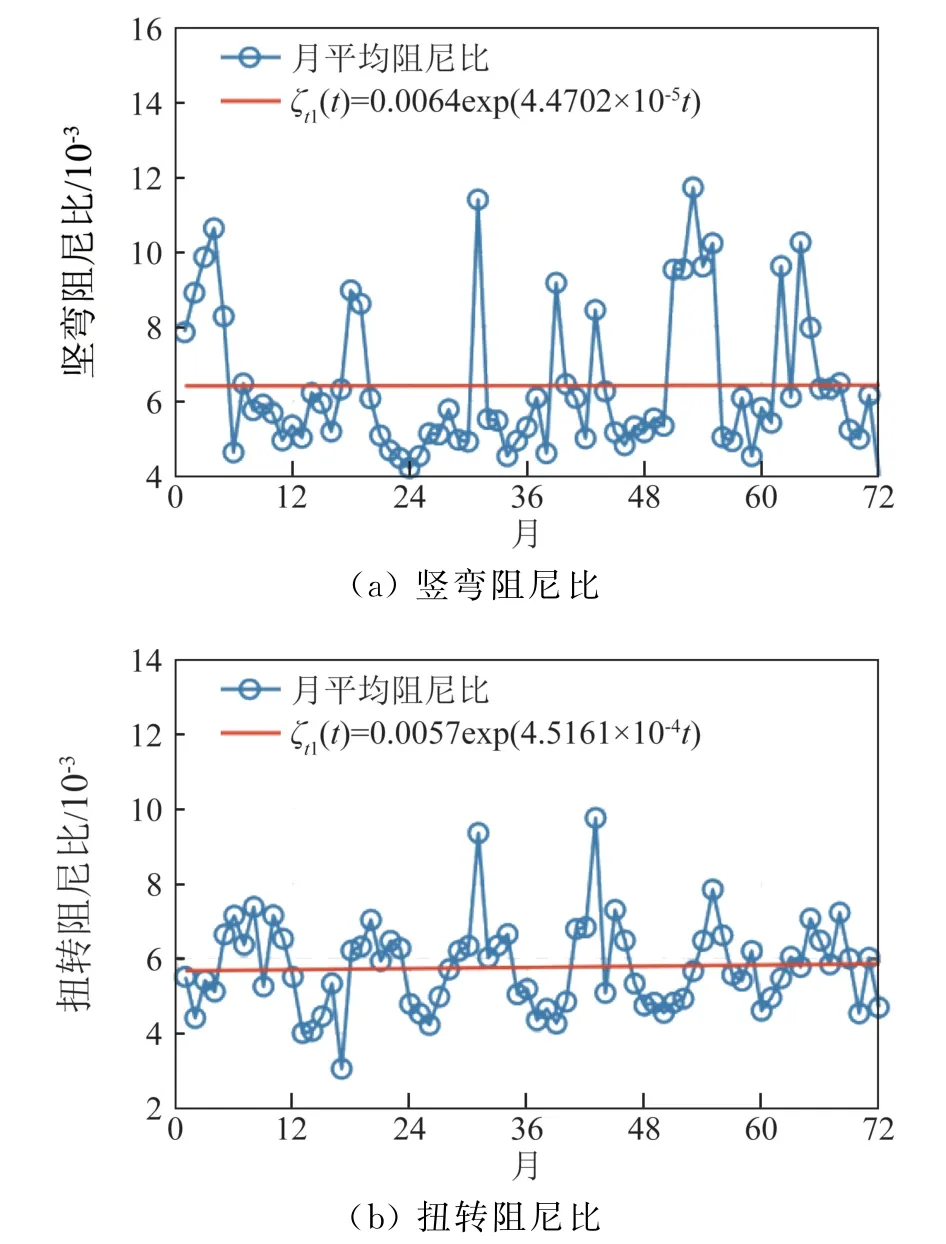
图21 西堠门跨海大桥阻尼比随时间变化趋势Fig.21 Variation trend of damping ratio of Xihoumen Bridge with time
4 涡振对来流的敏感性
4.1 来流攻角
在前面做纸条试验时会发现,纸条有时会“垂头丧气”、有时会“精神抖擞”,这与吹风机的风向有关。对于桥梁来说,风向也非常重要。将风向与桥梁结构横断面的夹角称为攻角(参见图22),较大攻角的风则会让桥梁异常“兴奋”。通常情况下,风的攻角小于3°,但当攻角增大到一定值后,不但引发了桥梁涡振振幅增大,还出现涡振区增多的现象。将相同的桥梁模型(图23)在7°攻角和0°攻角下进行对比,竖向振幅的试验结果可以相差几倍(参见图24)[26]。这充分体现了涡振对于来流攻角的敏感性。
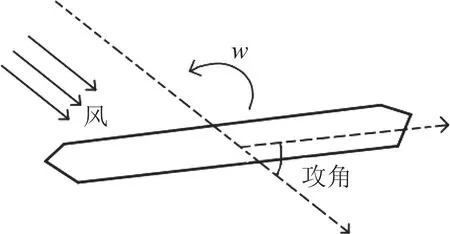
图22 攻角示意图Fig.22 Schematic diagram of incoming wind angle of attack
4.2 来流脉动效应
一般而言,近地面平均风速随着高度增加而增加。之所以要说平均,是因为在高山丘陵、地表起伏、城市建筑等的影响下,近地面风每时每刻的速度大小和方向都会发生改变,此时的风在这里我们称之为湍流。平均风速就像风速的“班级平均分”,代表了风的整体情况。任意时刻、任意位置的风的“个人成绩”则由平均风速与脉动风速组成。要想能更加全面的描述“班级情况”,则需要引入“标准差”,在这里我们称之为湍流度,I=u’/U,其中u’是风速的标准差,U是平均风速。
那较大的湍流度会产生什么样的影响呢? 均匀风吹过物体时,在物体表面产生旋涡脱落。而有了脉动部分的影响,旋涡脱落的频率变得不稳定,从而就抑制了涡振的产生。图25是用1540 mm×400 mm×67 mm的小尺寸模型分别进行均匀风和8%湍流度下的试验。在脉动部分的影响下,较大风速区间的涡振消失了,仅剩下低风速下的涡振,但涡振的幅度已经明显减弱(图26)[27],可以明显看出脉动部分对涡振的抑制作用。

图25 小尺寸模型试验[27]Fig.25 Test of small-scale model[27]
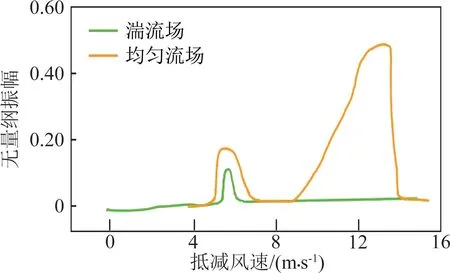
图26 湍流影响下的无量纲振幅(y/0.0067)[27]Fig.26 Dimensionless amplitude under the influence of turbulence[27]
4.3 风速与激励频率
为了探究来流风速对涡振响应的影响,将截面外廓为1.2 m×1.24 m的典型杆件简化为宽高比1.2∶1.24、阻尼比0.5%的矩形进行数值模拟(图27),得到表1。数据显示,当风速为25 m/s时,涡脱力频率θ 与桥梁结构固有频率ω=2.62 Hz最接近,此时最大位移为52.6 mm,远远大于其他位移值[28]。从表1中可以明显看出两个规律:一是当涡脱力频率θ 与结构固有频率ω 越接近,对应的最大位移越大;二是涡脱力频率随风速增大而增大。

图27 典型杆件截面计算简图[28]Fig.27 Calculation diagram of typical member section[28]
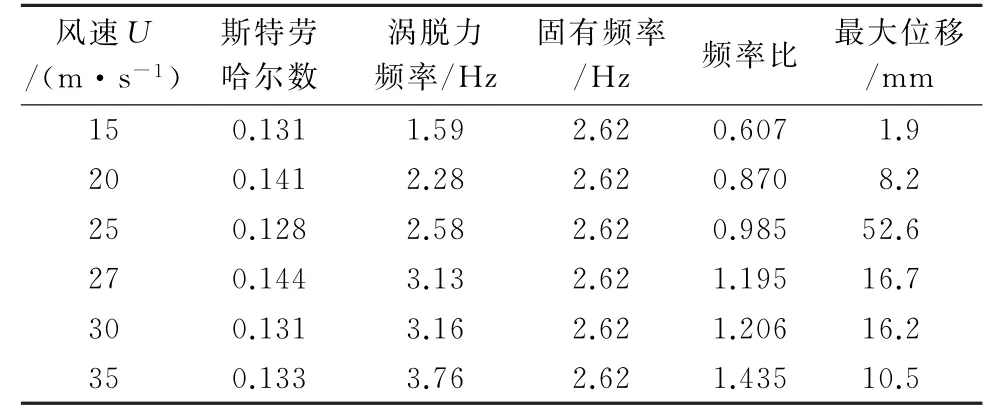
表1 风速影响[28]Table 1 Influence of wind speed[28]
将施加在物体上的大小、方向、位置随着时间不变或者变化很缓慢的力称为静载荷,随着时间显著变化的则称为动载荷。周期性的涡脱力就是一种典型的动载荷。大小相同的静载荷和动载荷作用在相同物体上,在惯性力的影响下,物体位移的大小是不同的。为了体现对位移的影响,引入动力放大系数μ=ymax/yst,式中动载荷作用下物体的最大动位移记做ymax,静载荷作用下物体的静位移记做yst。借用结构力学中共振效应度量关系,简化计算后得到式(1):
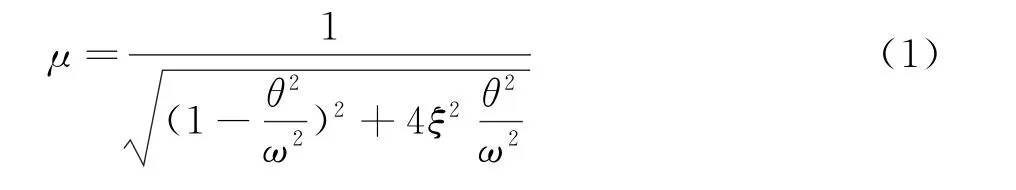
可以很明显看出动力放大系数μ 不仅与阻尼比ξ 有关,还与频率比θ/ω 有关。当阻尼比不变时,涡脱力频率θ 与结构固有频率越接近,即频率比越接近1,动力放大系数μ 越大(参见图28)。此时涡振振幅将不断增大,例如表1中,当θ=2.58 Hz时,最大共振位移达到表中最大值52.6 mm。这将导致涡激共振发生,涡脱力演变为载荷强度更大的涡激力。
无量纲参数斯特劳哈尔数(Strouhal number,简称St)是钝体绕流产生的涡脱力频率θ 与风速U 之比,记为St=θD/U,式中D 为结构特征尺寸。通过对丹麦大贝尔特桥引桥主梁断面的试验,得到了St随雷诺数的增加呈现先稳定后急剧增长而后重新稳定的变化规律,在低雷诺数下的St 略小于高雷诺数下的St(参见图29)[30],通常情况下桥梁断面的St约为0.2。因此在表1中可以明显看到,St 在0.128~0.144范围内波动,变化不大。由此可知,在St 一定时,不同的来流风速引起的涡脱力频率不同,进而影响动力系数使涡振振幅产生变化。
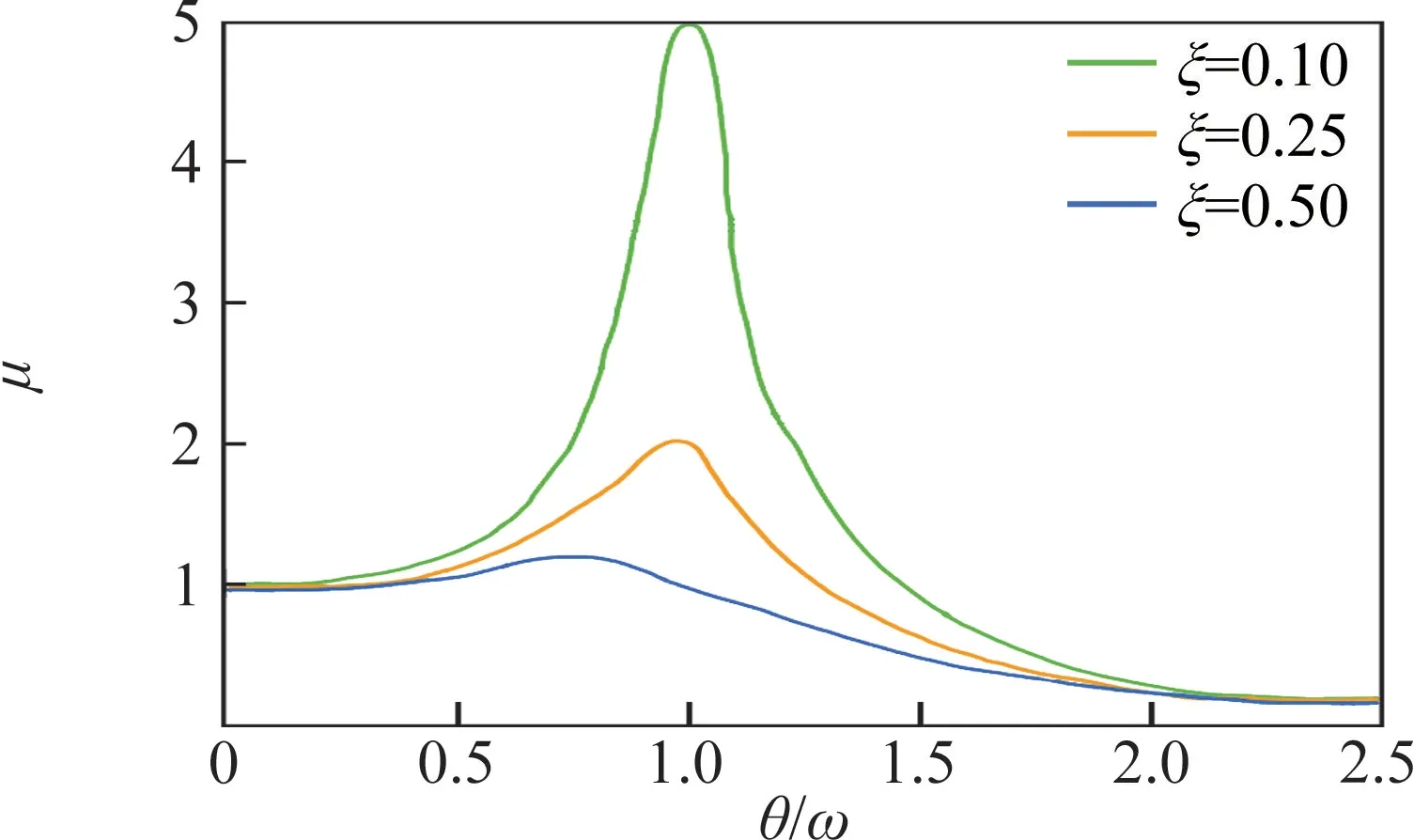
图28 动力放大系数与阻尼比、频率比的关系[29]Fig.28 Relationship between dynamic magnification coefficient and damping ratio,frequency ratio[29]
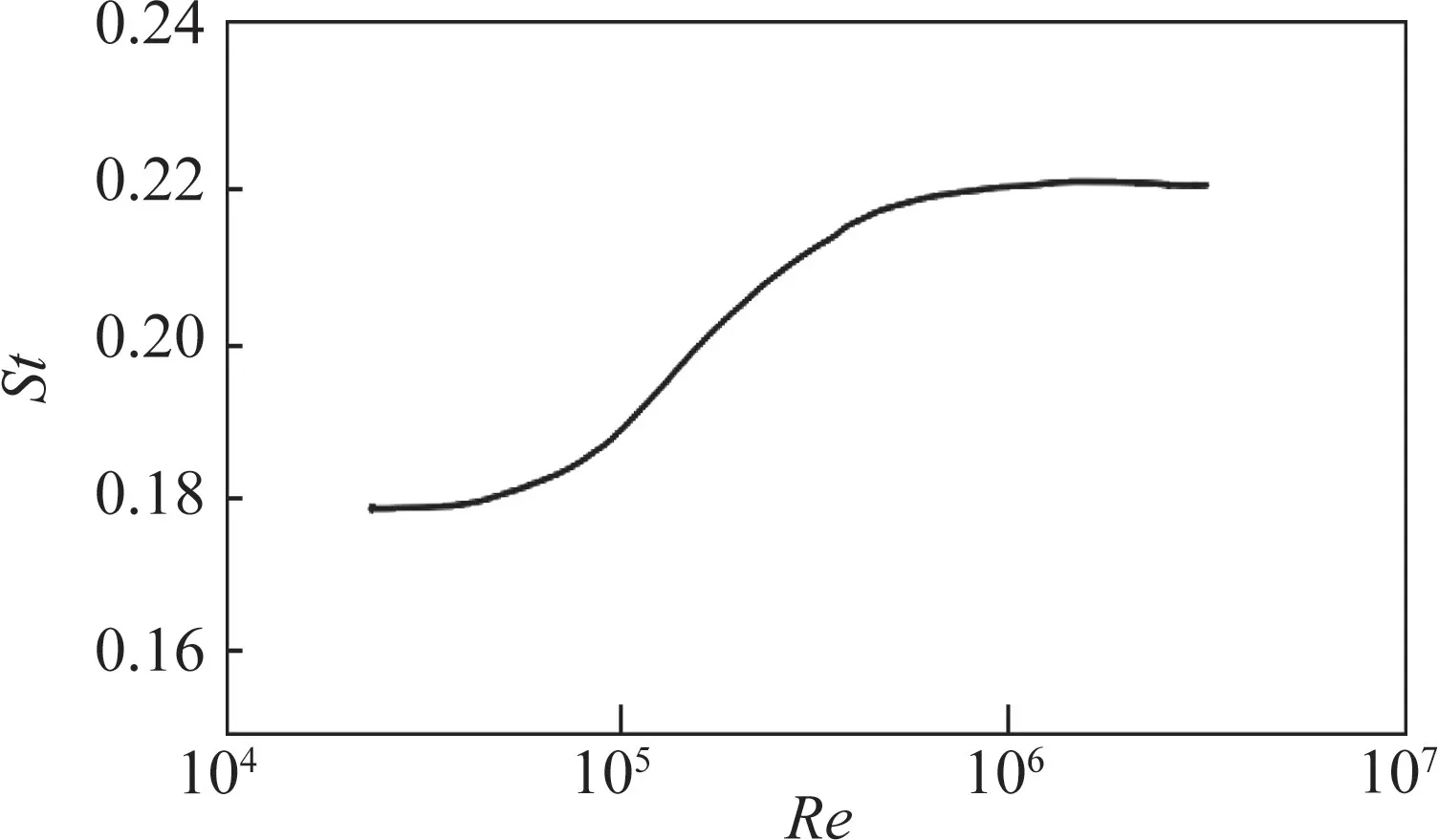
图29 Re 与St关系[30]Fig.29 The relationship between Re and St[30]
5 涡振的利用
尽管涡振可以影响桥梁结构的适用性,但利用其敏感性特征稍加改进则可以造福人类。涡街流量计就是利用了旋涡交替频率与流量有关的特性发明的,用来测量管道内的流量,目前已被广泛应用于工业生产中[31]。既然涡振如此常见,又积蓄大量能量,能否变废为宝利用涡振进行发电呢? 同济大学风工程研究团队发明了一种桥梁涡振控制与发电一体化的装置。在箱梁内侧安装压电片,涡振发生时所产生的涡激力导致结构的运动和变形再作用在压电片上,通过压电效应转化为电能,由此在有效抑制涡振现象的同时利用涡振敏感性进行发电。通过分别调整两侧压电片的安装高度使二者平齐或交错(参见图30b),从而实现在不同风况下均可达到较佳的发电功率和同时抑制涡振的效果[32]。哈尔滨工程大学也发明了一种仿生结构的风力发电机(图31),利用低风速下产生的周期性旋涡引发结构产生周期性振动和变形,再通过PVDF材料将形变能转化为电能[33]。
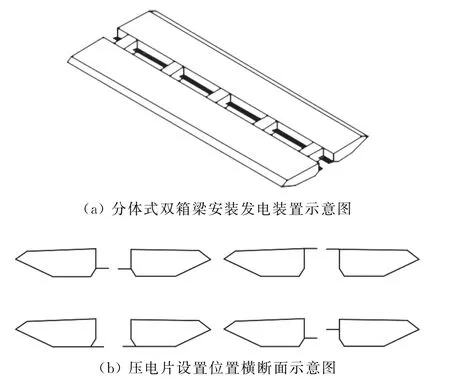
图30 桥梁涡振控制与发电一体化装置示意图[32]Fig.30 Schematic diagram of bridge vortex-induced vibration control and power generation device[32]
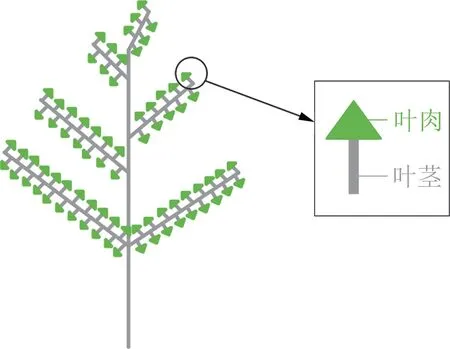
图31 “树枝”仿生发电机示意图Fig.31 Schematic diagram of“branch”electric energy generator
6 结 论
综上所述,最近发生的多座桥梁的涡振现象并非是由桥梁结构损伤所引起,涡振发生的最根本原因是涡振自身的高敏感性。本文从涡振产生机理出发,讨论了结构外形尺寸、来流参数、阻尼比等参数变化对涡振产生的影响。经对比分析可知涡振具有结构外形尺寸的高敏感性,敏感度一般可达结构特征尺寸的1/10甚至1/100,拉索表面粗糙度乃至涂层材料也会对涡振响应产生一定影响。结构阻尼比、来流攻角、湍流度与来流风速等参数也都对涡振有着显著影响。
但在对涡振进行安全控制的同时,也可以利用涡振的高敏感性,实现能量的合理开发利用。在试验室层面,涡振发电已成为现实。未来涡振发电利用的深入研究工作值得期待。
致谢:“风吹粘附在圆柱体上的纸带”试验借鉴了东莞理工学院马宏伟教授的《工程力学》教学视频(图6)。同济大学风工程研究团队吴风英博士研究生提供了主梁绕流数值模拟结果(图8),初晓雷硕士研究生提供了浙江舟山西堠门跨海大桥阻尼比随时间变化结果(图21)。在此一并表示感谢。

