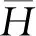炸药背基对爆炸冲击载荷的影响分析

刘聪，张世联

(上海交通大学 船舶海洋与建筑工程学院，上海 200240)

对于自由场爆炸载荷作用下板结构的动力响应问题已有相对较多、较全面的研究。对于内部爆炸，由于密闭空间的限制作用，冲击波会在结构内部发生多次反射和汇聚，导致目标板出现二次或多次加载的情况，同时密闭空间内会存在较长时间的持续高压(准静态压力)，其冲击过程较复杂。众多学者在内爆载荷[1，2]、密闭结构的变形[3-5]和破坏模式[6]，以及准静态压力[7]等方面亦取得了一定的研究成果。但是理想的自由场和密闭环境在工程实际中非常少见，更多的冲击环境介于这两者之间。比如，当炸点或者目标板附近存在障碍物时，或者当容器的一面或多面敞开的时候。工程实际中的一个典型情况是背基爆炸，即炸药被放置在地面、水泥或刚性基座上进行引爆。与内部爆炸相似，发生背基爆炸时，炸药背基会将冲击波向目标板反射，使目标板受到更大的冲击载荷。但不同的是准静态压力却不会产生。因此，背基爆炸问题值得探讨。已有的研究通过试验和仿真的方法分析炸药背基对金属板所受爆炸冲量和塑性变形的影响，发现在炸药下方布置刚性背基后，炸药上方的金属板受到的脉冲值和塑性变形均显著增大[8]。但是并未对这种现象进行规律性的研究。为此，考虑以一正方形固支方板为对象，通过改变炸药质量和相对爆距，分析背基爆炸时爆炸冲量增强幅度随这些参数的变化规律，提出背基爆炸冲量增强因子的经验计算公式。

1 计算模型

1.1 几何模型

建立自由场爆炸和背基爆炸几何模型见图1。自由场爆炸模型由一块固支正方形板和一个半球形炸药组成。其中，方板的半宽值L=100 mm、厚度t=3 mm，半球形TNT炸药位于方板中心点正上方H处，见图1a)。背基爆炸模型在自由场爆炸模型的基础上，在半球形炸药背后布置一个固定刚性壁，见图1b)。

图1 爆炸模型

定义相对爆距为

(1)

1.2 材料模型及参数

板的应力与应变关系近似为双线性弹塑性材料，以真实应力对应等效塑性应变的方式处理。密度7.85×103kg/m3，弹性模量2.1×105MPa，泊松比0.3，静态屈服应力235 MPa，硬化模量250 MPa，失效应变0.28。采用能考虑动态应变率效应的Cowper-Symonds模型，同时考虑材料应变强化效应，其本构方程如下[9]。

(2)

(3)

采用gamma律状态方程EOSFAM描述空气：

p=(γ-1)·ρ·e

(4)

式中：e为单位质量比内能，取0.21×106J/kg；ρ为空气密度，取1.25 kg/m3；γ为比热比，取1.4。

TNT炸药用高能密度空气模拟，其密度为1 600 kg/m3，能量密度为4.2×106J/kg。

1.3 耦合模型

采用MSC.Patran进行有限元建模，限制目标方板四边节点6个自由度全部为零。目标板以拉格朗日单元模拟，炸药和空气以欧拉单元模拟，二者以一般耦合法进行耦合。采用瞬态非线性动力学分析程序MSC.DYTRAN对模型进行计算，欧拉单元采用具有二阶精度的ROE求解器进行求解，拉格朗日单元采用显示积分方法对时间域进行求解，计算时间为3 ms。

根据一般耦合法的要求，在建模时需要添设虚元与拉格朗日单元组成封闭六面体耦合面。自由场爆炸和背基爆炸耦合模型见图2。

图2 有限元模型耦合面示意

在自由场爆炸的耦合模型中，目标板为拉格朗日单元，其他五面为虚元，设置爆炸冲击波可自由通过虚元，见图2a)。在背基爆炸耦合模型中，目标板为拉格朗日单元，炸药背基为虚元，并设置冲击波不可通过该虚元，其他四面仍为可通过的虚元，见图2b)。

1.4 网格密度

采用大小不同网格对爆距为100 mm、炸药质量为60 g时自由场空爆载荷下目标方板的动力响应进行试算。所选用的网格大小及计算结果见表1。

表1 网格参数及计算结果

根据表1计算结果的收敛性并综合考虑仿真计算的时效性，选择网格尺寸为4 mm×4 mm。相应目标板有限元模型及坐标系见图3，其中长、宽和高度方向分别为x、y和z轴方向。

图3 方板有限元模型

1.5 计算工况

采用控制变量法，对不同炸药质量和相对爆距时，目标方板所受到的爆炸冲量进行计算。计算工况见表2。

表2 计算工况

2 计算结果与分析

2.1 炸药质量的影响

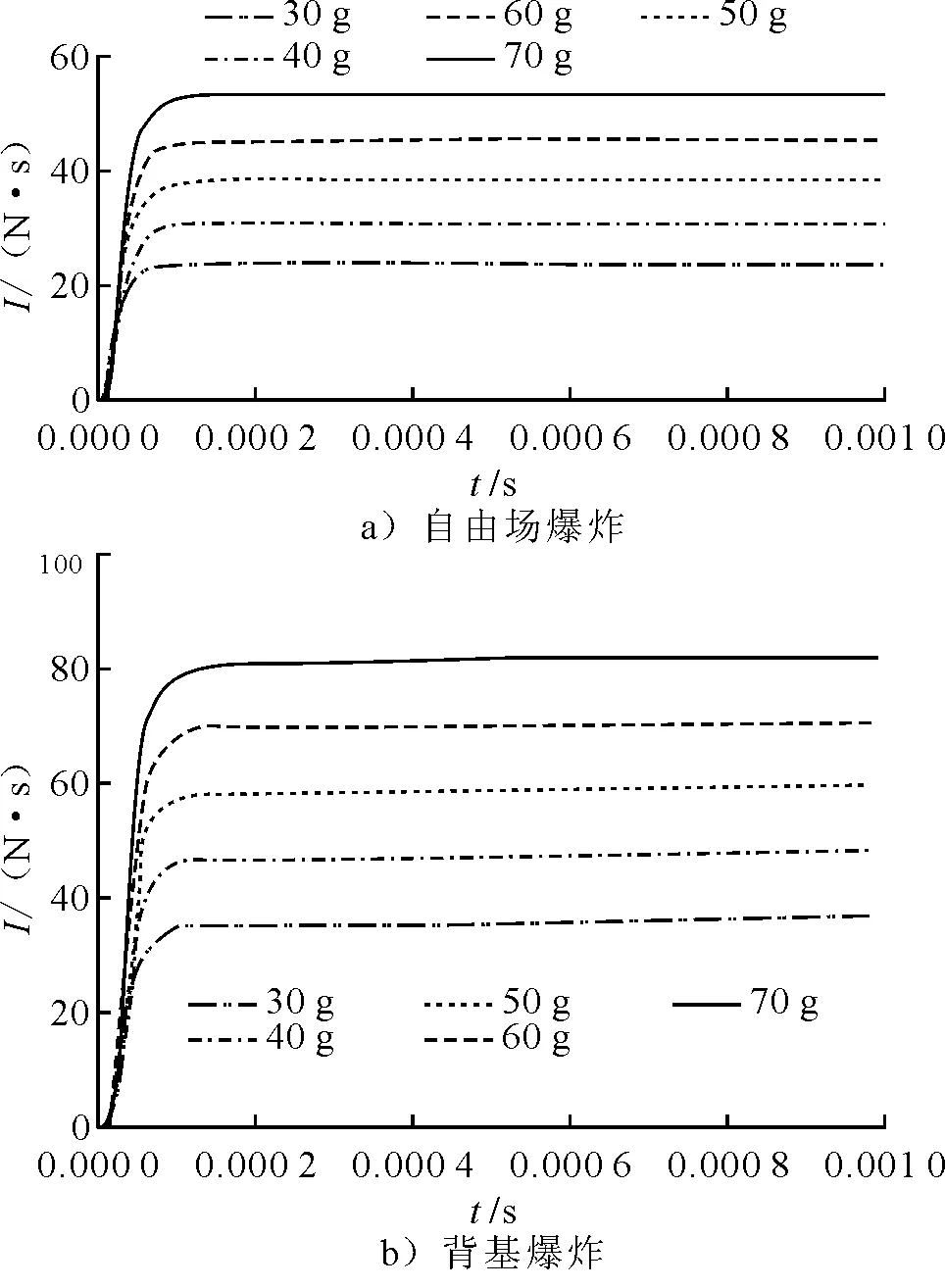
图4 不同炸药质量下爆炸冲量时历曲线

由图4可知，炸药质量相同时，背基爆炸的爆炸冲量显著大于自由场爆炸的爆炸冲量。这是因为炸药背基阻止了爆炸冲击波向后方传播，并将这部分冲击波向目标板反射，从而增加了作用在目标方板上的冲击波总量，因此，冲击载荷增大。

为了量化的研究炸药背基对爆炸冲击载荷的增强效果，定义冲量增强因子为

(5)

式中:Ib为背基爆炸时目标方板受到的爆炸冲量；I0为自由场爆炸时目标方板所受到的爆炸冲量。

3种相对爆距在不同炸药质量下(case 1～case 11)对应的冲量增强因子见图5。

2.2 相对爆距的影响

图6 冲量增强因子随相对爆距变化趋势

根据图6中冲量增强因子随相对爆距的变化趋势，总结出如下双折线形式的经验公式。

(6)

根据式(6)计算case 12～case 23的冲量增强因子，结果见表3。

表3 冲量增强因子ω仿真与公式计算结果对比

由表3可知，各工况下经验公式计算结果与仿真结果间的误差均在2%以内，说明该公式具有很好的准确性。

3 结论