船模阻力CFD结果的不确定度分析

张立，周传明，陈伟民，陈建挺

(上海船舶运输科学研究所 航运技术与安全国家重点实验室，上海 200135)

CFD技术是船舶水动力领域的关键技术之一，是船舶性能评估、线型优化等方面的重要且高效的工具[1]。CFD方法虽然高效，但是其计算效率和精度受到使用人员的经验、计算模型设置等因素的影响，甚至在某些情况下出现较大误差[2-3]。因此，针对CFD计算精度的分析就显得十分必要。

关于CFD不确定度分析,早期的研究大多是基于网格收敛性的CFD不确定度分析，如针对特定湍流模型和特定壁面条件下，对结构化网格或非结构化网格的数值模拟过程进行不确定度分析[4-6]；使用不同的湍流方法对船模CFD计算结果进行验证和确认[7]，来比较不同湍流模型之间的不确定度分析的差异；有部分研究通过方差分析的方式对CFD数值模拟进行不确定度分析[8-9]，此方法所依赖的前提是数值模拟结果随着因素变化呈现正态分布趋势，但是这种前提并未得到验证。因此，CFD不确定度的分析方法仍然处于探讨阶段，一套统一的分析方法并未建立。近期的研究趋向通过提升分析因素的维度来比较CFD不确定度分析之间的差异，如不同船型、不同尺度、不同湍流模型及不同壁面条件等维度。

针对CFD计算结果在不同壁面条件(Y+)下的不确定度差异问题，考虑基于1艘模型长度为7.455 2 m的标准船模，基于k-ε湍流模型，设置不同壁面条件(Y+=60、120、240)，并分别设置3套不同密度的网格尺寸，对其进行船模阻力CFD模拟，在前序进行多维度仿真的基础上，参考ITTC关于CFD模拟的不确定度规程，对数值模拟结果进行不确定度分析，即验证和确认(V&V)。

1 原理

1.1 CFD计算方法

CFD湍流模型分为DNS、LES、RANS等。RANS方法通过简化N-S方程，控制方程和连续性方程如下式所示。该方法降低了计算难度，也提升了计算速度，深受工业界青睐。

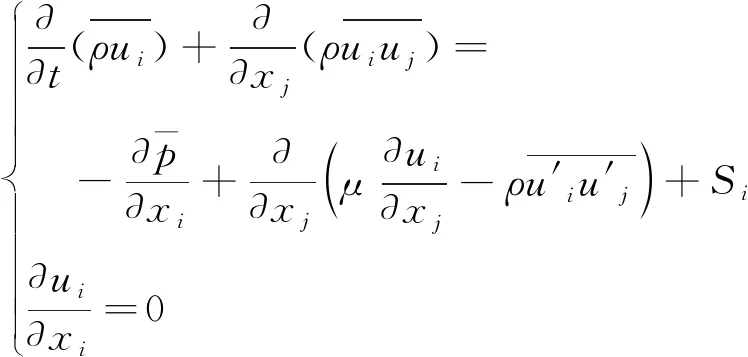
(i,j=1、2、3)

(1)

在计算船模阻力时，将速度进口、压力出口、自由液面、船体壁面等作为边界条件。

1.2 分析要素的选择

基于RANS方法的湍流模型有很多变体，不同的湍流模型具有不同的适用性，在求解数值结果时，湍流模型的选择对结果产生重要影响。网格密度对计算结果收敛性有明显影响。离散格式主要对计算效率造成影响，但对结果精度的影响十分有限。在近壁面处的流动，由于是从黏性底层到湍流的转化，需要壁面函数处理。RANS方法通过壁面函数控制近壁面处流动问题，通过壁面函数结合湍流模型求解计算域，通过引入无量纲数值Y+进行控制。对于时间步长，当设置的时间步长满足相应的库朗数要求之后，近似认为时间步长对结果的影响可以消除。根据文献[8]，除了湍流模型外，船模阻力仿真结果主要受网格密度、近壁面处理的影响，因此，本文针对不同近壁面条件，设置不同网格密度分析其不确定度。

2 CFD不确定度分析方法

对于数值模拟结果S和真值T之间的误差δS，可以分为模型误差δM和数值误差δN，见图1。

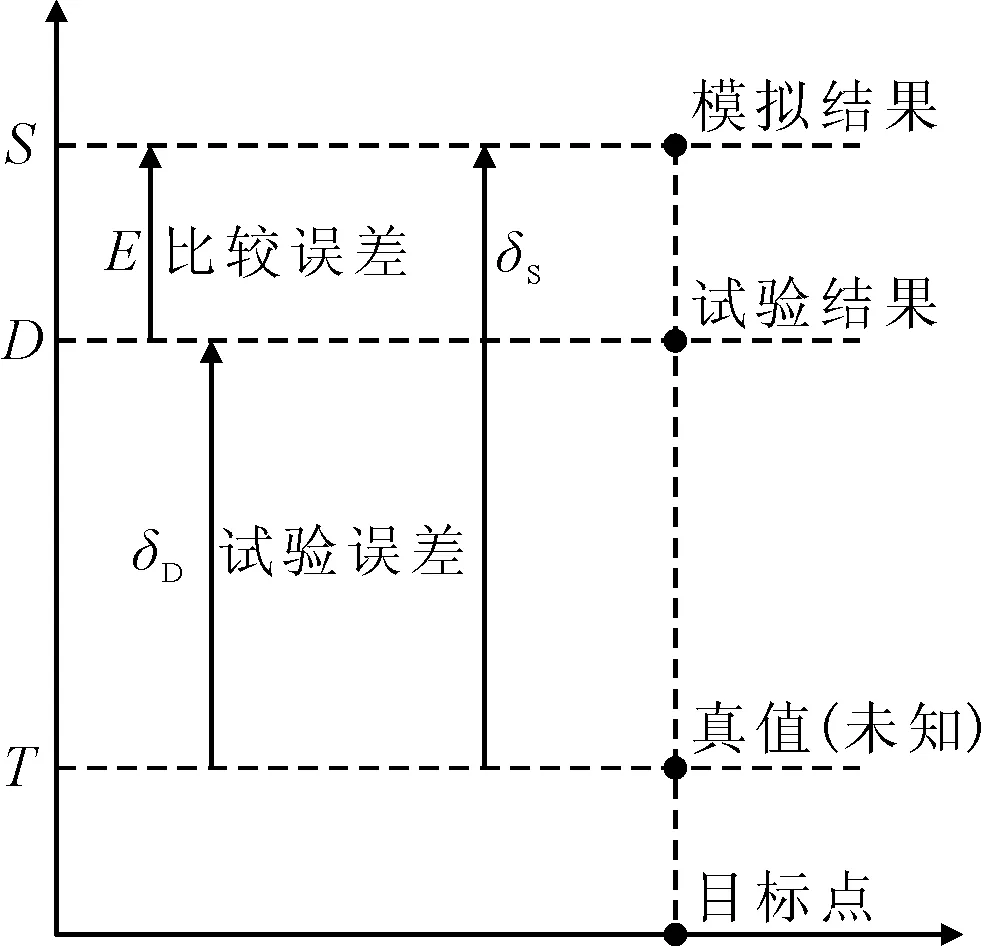
图1 CFD模拟的误差示意

其中，模型误差是对物理问题进行描述时候带来的误差，数值误差是因为数值求解过程中因数学方程求解带来的误差[10]。因此，CFD数值模拟时需要分别进行分析，分析过程分为2个步骤(V&V)：①验证，评估数值结果的不确定度；②确认，评估数值结果的正确性。通常意义上的V&V是一个分析过程，这与船模试验不确定度分析有所不同。

2.1 验证

当对船模阻力进行CFD模拟，其数值结果因不同的湍流模型、网格密度、近壁面条件、时间步长及其他因素等多种因素影响。因此，当湍流模型和Y+一定的时候，CFD模拟的不确定度表示为

(2)

式中：UI、UG、UP分别为迭代误差、网格收敛性、以及其他因素的不确定度。

迭代误差是由于每个计算步骤中的当前解与精确解之间的误差造成的，截断误差主要是因为数值求解过程中高阶项的舍入造成的。

对于迭代误差，当计算结果是取一段较长时间的均值，且计算结果为单调收敛的趋势，则该项误差为小量，迭代误差可按照收敛结果上下界之半(yU-yL)/2来计算。其中yU、yL分别为计算收敛结果的上下限。

按照三角分布计算，迭代误差不确定度为

(3)

目前的CFD不确定度分析方法中，截断误差根据网格收敛性进行分析，通过定义统一的网格增长比，划分多套网格，分析其收敛性，然后通过外推法对结果进行估计[11]。

因此，通过上文的分析，便可以对数值模拟的结果进行验证。

2.2 确认

对数值模拟的结果进行确认的过程，也是将数值结果与试验结果和真值进行比较的过程。确认是利用基准试验数据评估数值模拟的模型不确定度UM的过程。试验结果D和数值模拟S之间的误差即为比较误差E，即

E=D-S

(4)

其中，试验结果D带有测量不确定度，S取值SGF，即为细化网格的数值模拟结果。

数值模拟结果S包含模型误差δM和数值误差δN，即

E=D-S=δD-(δM+δN)

(5)

数值模拟结果的确认过程的不确定度UV为

(6)

式中：UD为试验结果的不确定度；UN为验证过程中的数值不确定度。

通过式(4)～(6)，便可以比较UV和E的结果是否得到确认。当UV>|E|，则UV在该层次得到确认；如果UV≪|E|，则表明数值结果偏离试验值较远，需要改进计算模型。

3 标准船模阻力结果分析

针对标准船模的CFD阻力结果进行不确定度分析，通过湍流模型、网格密度和Y+3个方面对数值结果进行验证，同时结合所进行的试验结果对CFD不确定度进行确认。

在湍流模型选择上，选择标准k-ε湍流模型；网格划分方面，使用三维非结构网格，网格总数的加细比约为rG=2；Y+值的增速rY+=2,见表1。

3.1 计算模型

船模主尺度，船模速度及相关参数见表2。

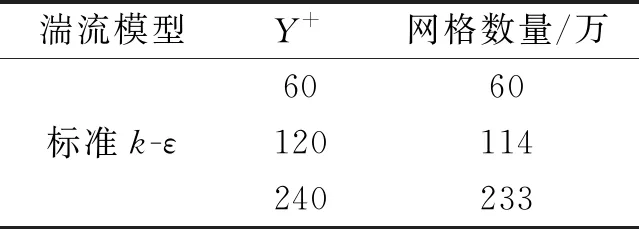
表1 CFD不确定度分析计算设置

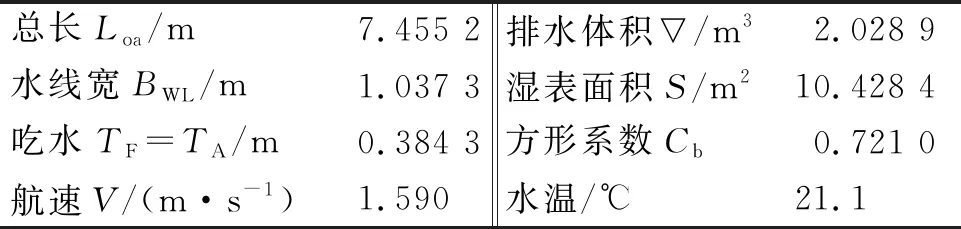
表2 船模主尺度

3.2 验证

通过设计计算矩阵，对船模阻力进行CFD模拟，半船计算结果见表3。

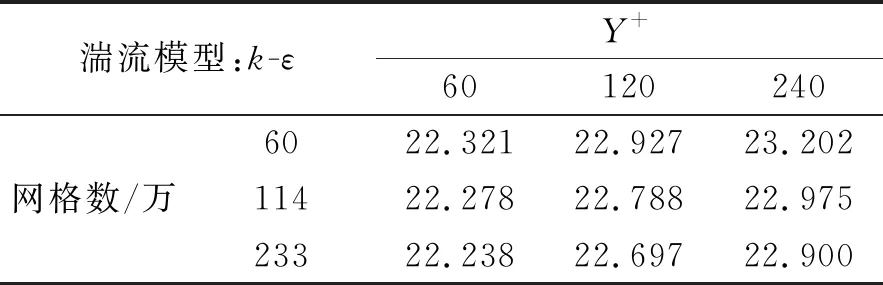
表3 标准k-ε湍流模型的计算结果

3.2.1 验证方法

此前的计算结果中，与常规的CFD不确定度分析不同：选择2个维度上的分析，需要分别进行验证。收敛因子RG为

(7)

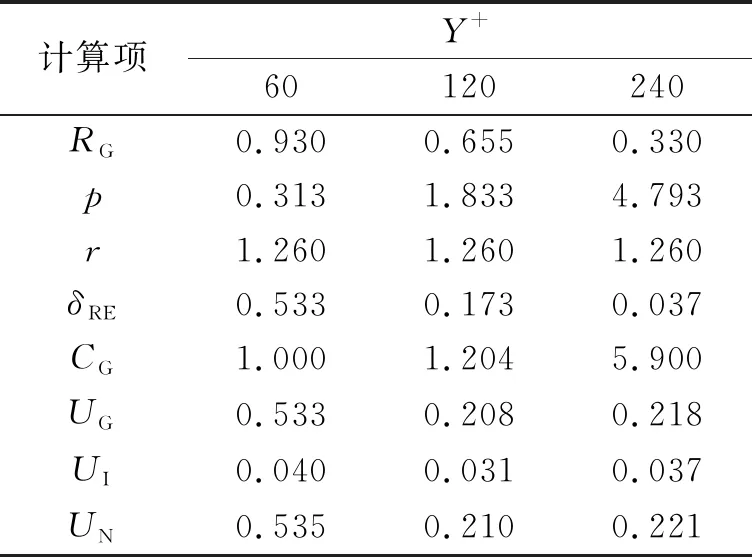
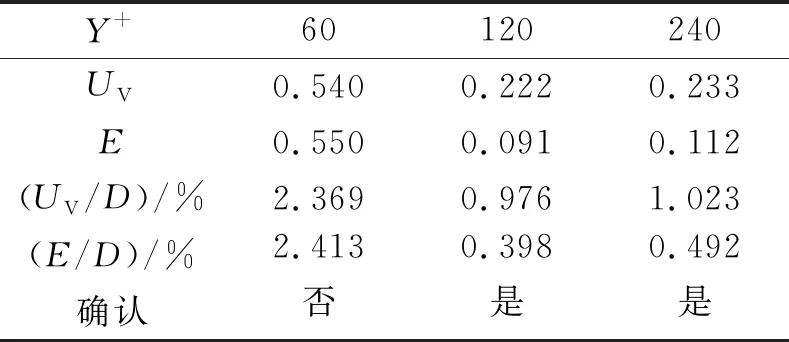
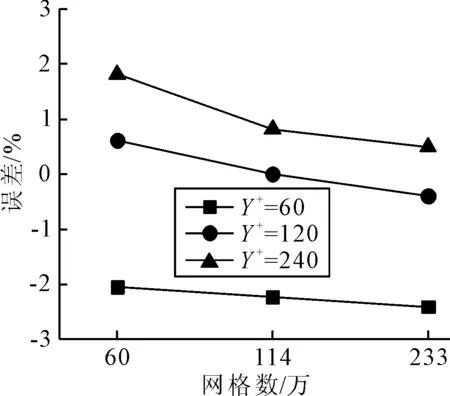
式中：SGF、SGM、SGC分别表示细网格、中网格和粗网格的结果。当0

(8)

误差修正因子CG为

(9)

根据ITTC(2017)建议，当误差修正因子CG<1时，

UG=[2|1-CG|+1]·δRE

(10)

当CG远小于或者远大于1时，网格的不确定度为

UG=[|CG|+|1-CG|]·δRE

(11)

3.2.2 数值不确定度

根据式(2)计算得到验证过程中的不确定度UV，见表4。

表4 不同Y+值计算结果的数值不确定度

3.3 确认

对相同条件的船模进行拖曳水池试验，总阻力测量结果RT=22.789×(1±0.32%)，其中0.32%为试验结果的不确定度。在得到数值不确定度之后，确认过程的不确定度UV见表5。

表5 确认过程的不确定度

表5表明，当Y+=60时，由于UV

3.4 改进数值模拟的方法

如图2所示，整体而言，本文数值模拟结果的误差在3%以内，与其他相关文献相比，本文的数值模拟结果具有较高精度。但是，Y+=60的结果并未得到确认，而Y+=120和240的结果得到了验证和确认。从不确定度分析的角度上，Y+=60的分析过程应当使用更多套的网格进一步分析，同时也说明当Y+值选择不合适的时候，即使对网格进行加密并不一定能获得收敛结果或高精度结果。因此，在进行数值模拟时，Y+值要与湍流模型相匹配。

图2 k-ε计算结果误差

4 结论

1)Y+值对不确定度分析结果产生了明显影响，即使采用相同的网格收敛验证方案，不同Y+值时的不确定度分析结果不相同。

2)从本文的数值模拟结果发现，Y+值对数值模拟的结果影响比网格密度的影响更大；针对k-ε湍流模型，并非Y+值选择越小，计算结果精度便越高。需经过多次校验，合理设置计算模型才能够提高计算结果的精度。

3)通过比较结果，使用多套网格增加网格收敛性的验证，能够提升计算结果的可信程度。