操舵仪性能评比中舵阻力能耗评价指标设计

张智颖，刘勇，陈永冰，李文魁

(海军工程大学 电气工程学院，武汉 430033)

船舶自动操舵仪是船舶操纵控制系统中的重要组成部分，可控制舰船按照预定的航向或航迹航行，其性能的好坏直接影响船舶航行的操纵性、安全性和经济性[1]。不同操舵仪由于控制律、操舵控制方法不同，其控制精度与能耗有所差异[2]。以往学者对操舵仪控制性能的测评，大多关注控制算法及其精度，忽略了不同控制方法带来的能耗损失[3]。有学者曾提出针对航向自动舵的航向控制性能指标，将航向均方差同操舵大小相联系，航向均方差与操舵舵角平方的综合计算结果越小，自动舵航向控制性能越好[4-5]。尽管该指标同时考虑了航向控制精度和舵阻力能耗的影响，但因只针对航向自动舵的航向控制模式，对于航迹自动舵的航迹、迹向等控制模式，该性能指标不再适用。为此，考虑针对操舵引起的舵阻力能耗进行试验，采用理论公式推导及周期性摆舵仿真试验验证的方式设计舵阻力能耗评价指标。运用该舵阻力能耗评价指标的计算结果比较不同操舵仪的性能优劣。

1 能耗求取

现有常规舰船的4自由度MMG模型[6]，已通过系列约束船模试验确定了各类流体动力导数和干扰系数，其公式如下。

(1)

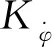
1.1 舰船纵向运动受力分析

根据敞水实验结果并进行回归分析得到XHH关于纵速u的一元三次回归表达式。

XHH=-(au-bu2+cu3)

(2)

式中：a、b、c为常数系数。

XHP求取表达式为

(3)

式中：t为推力减额分数；ρ为流体密度；n为螺旋桨转速；Dp为螺旋桨的直径；WP0为船舶直航时桨处的伴流分数；kt为推力系数，可表示为J的函数，其系数K0、K1、K2由螺旋桨敞水特性曲线回归得到[7]。

XHR求取表达式为

(4)

式中:AR为舵叶面积;δ为舵角;V为纵向速度与横向速度的合速度;CN为该舰舵法向力系数，其求取公式中fα为升力系数在冲角为零时的斜率，对确定的船型其为常数[8]；αR为流入舵的有效冲角，求取公式如下。

(5)

其中：vR为流入舵的有效横向速度，计算公式如下；uR为流入舵的有效纵向速度，近似取uR≈V。

vR=vRp-γR(v+lRr)

(6)

式中：vRp为正舵时，因螺旋桨单向旋转的不对称作用而引起的横向平均流速；γR是考虑船体整流作用的修正系数。合并式(5)与式(6)有

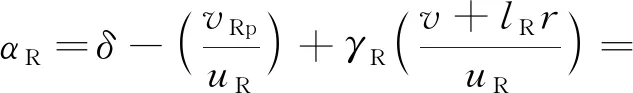
(7)

其中：

(8)

忽略因螺旋桨单向旋转的不对称作用而引起的横向平均流速vRp，式(4)中舵阻力XHR的求取公式可表达为

(9)

1.2 阻力能耗计算公式

已知功耗的计算可表示为力与速度的乘积在时间上的积分。一般舰船横向速度v比纵向速度u小得多，因此计算合成速度V时u起显著作用[9]，取近似V≈u，在只考虑单舵情况下，结合式(9)，克服舵阻力能耗可表示为

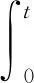
(10)

为对比舵阻力能耗的影响，继续求取舰船克服水对裸船体的阻力XHH造成的能耗。由式(2)得到克服水阻力XHH造成的能耗近似计算式。

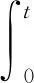
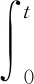
(11)

2 典型操舵方式下舵阻力能耗占比

2.1 舵阻力能耗计算

设计周期性摆舵仿真试验：初始航速18 kn，舰船作近似匀速直航运动，利用MATLAB软件对舰船MMG模型进行仿真。

1)设置一组对照组，在不打舵情况下直线航行800 s，得到航行距离及推进总能耗等相关数据。

2)设置操舵速率为2.5和5.0 (°)/s，操舵最大幅度在2°～12°之间的6组舵角正弦变化的周期性摆舵仿真试验，航行距离与步骤一得到的航行距离相同，分别按照式(10)与式(11)计算能耗EXHR与EXHH。

3)记录以上13组试验完成同样航行目标所经历的时间，该过程克服的水阻力能耗EXHH及舵阻力能耗EXHR。

最大操舵幅度2°、12°下的周期性摆舵仿真试验得到舰船纵向速度、横向速度随时间变化见图1、2。

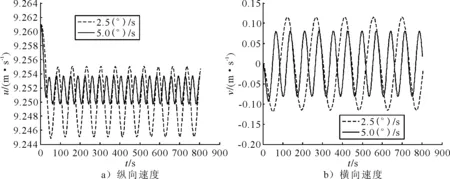
图1 2°最大操舵幅度下周期性摆舵仿真

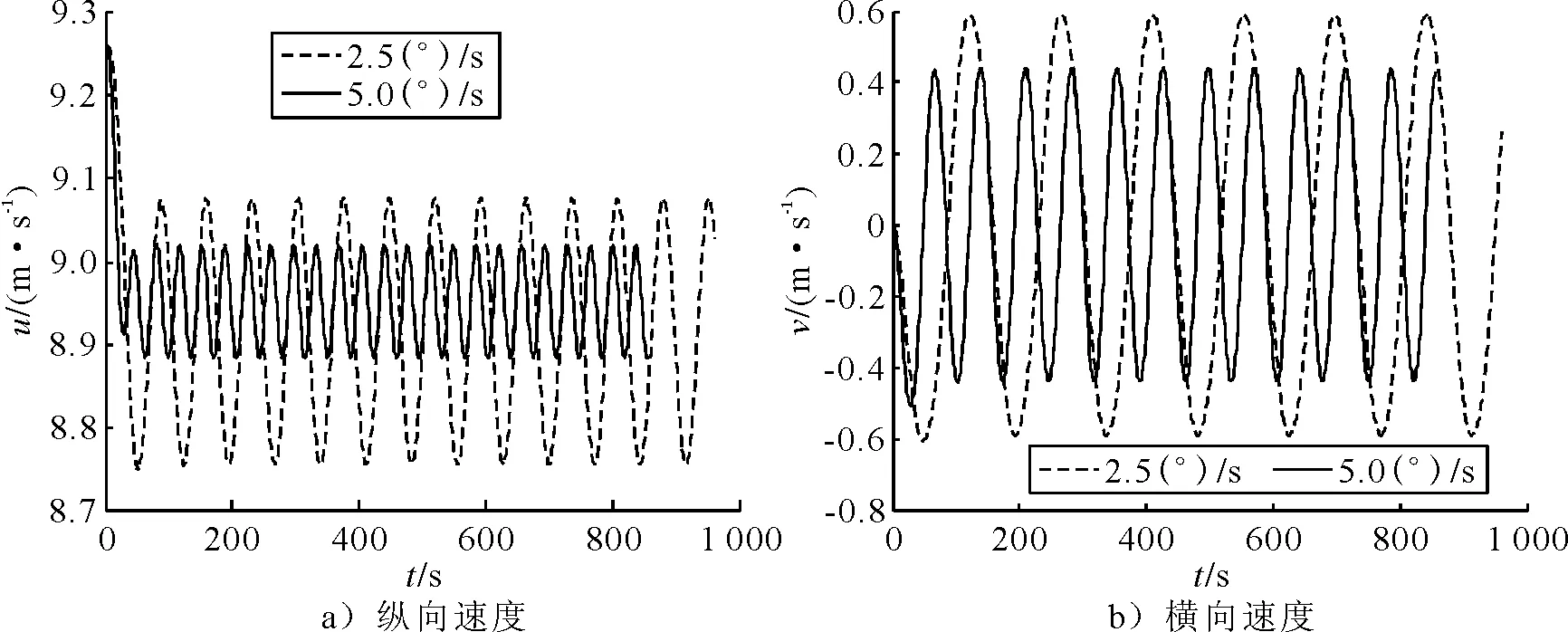
图2 12°最大操舵幅度下周期性摆舵仿真

从图1、2可看出，操舵幅度越大，纵向速度及横向速度振荡的幅度越大；操舵频率越大，纵向速度及横向速度振荡的幅度越小。分析周期性摆舵仿真试验结果，得到不打舵情况下，在800 s时间内舰船航行7 399.54 m，克服水阻力能耗2 384.61 MJ。2种操舵速率下的操舵仿真试验能耗计算结果见表1、2。

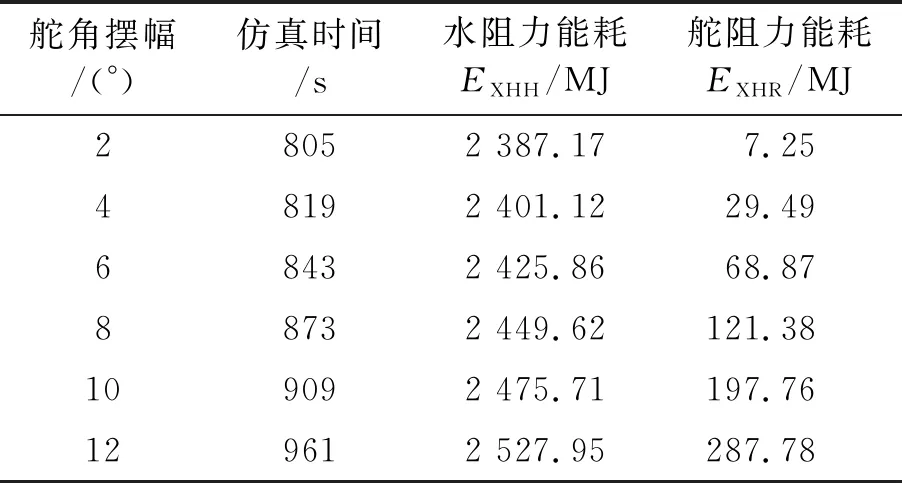
表1 2.5 (°)/s操舵速率下的操舵仿真试验能耗计算结果

对比表1、2，在同一操舵速率下，随着最大操舵幅度的增加，完成同样航行任务所耗费的时间增加，克服水阻力能耗有小幅度的增加或减少，舵阻力能耗大幅增加，由最初的约7 MJ升至约200 MJ。同一最大操舵幅度下，操舵速率越大，完成同样航行任务所耗费的时间减少，克服舵阻力能耗增加，克服水阻力能耗基本一致。

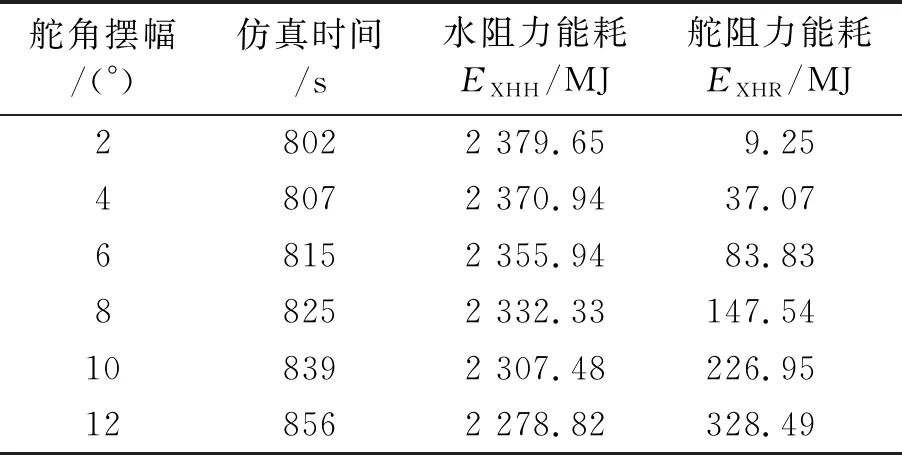
表2 5.0 (°)/s操舵速率下的操舵仿真试验能耗计算结果

2.2 舵阻力能耗占比分析

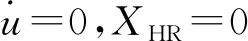
按照式(12)计算舵阻力能耗占总能耗的比例，结果见表3。

(12)

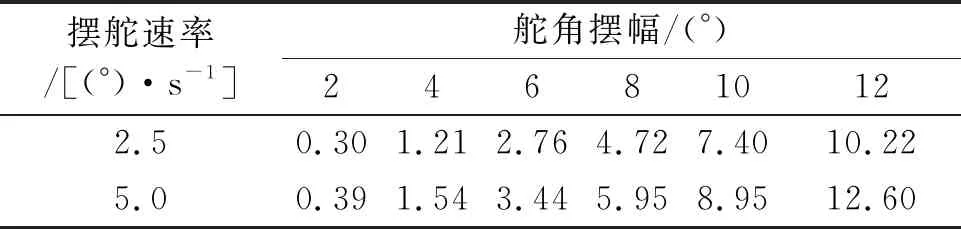
表3 舵阻力能耗占总能耗比例

由表3可见，随着操舵幅度的增大，舵阻力能耗所占的比例由最初的约0.3%升至约12%，即使整个航行过程只控制1/3的时间操舵，舵阻力能耗占比最高也可达4.2%，舵阻力能耗的影响不可忽略。同一操舵幅度、不同操舵速率下的舵阻力能耗占总能耗的比例相近。

3 舵阻力能耗评价指标设计及验证

3.1 舵阻力能耗评价指标设计

在舵阻力能耗占比分析的基础上，对舵阻力能耗求取式(10)做适当简化，据此设计舵阻力能耗的评价指标。

进一步简化，现讨论式(13)中能否忽略无因次化的v′，以式(14)代替。

(14)

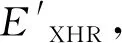
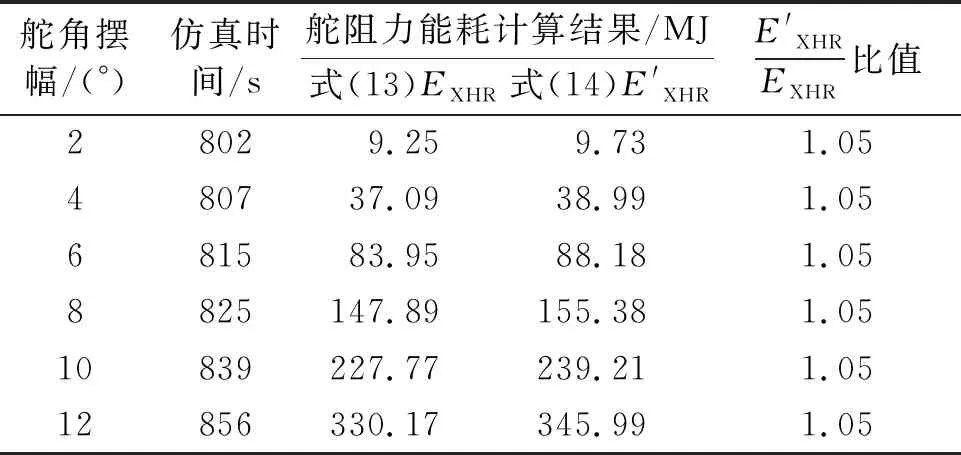
表4 舵阻力能耗近似求取比较结果

由表4可见，忽略无因次化的v′后的计算结果与忽略前的结果差别不大。确定舵阻力能耗的求取可采用式(14)。此外，对同一艘舰船，尽管在周期性摆舵方式下，图1～2都可说明纵向速度u的变化很小，式(14)中影响舵阻力能耗大小变化的主要是舵角变化。因此，设计舵阻力能耗评价指标ζ见式(15)。

(15)

式中:T为完成航行目标所用时间。

利用2.1中设计的操舵速率为5.0 (°)/s，操舵幅度不同的6组周期性摆舵仿真试验，按照式(15)计算得到能耗评价指标结果见表5。

表5 舵阻力能耗评价指标计算结果

3.2 舵阻力能耗评价指标验证

分别对能耗评价指标及2.1的舵阻力能耗占比结果进行归一化处理。将不同最大操舵幅度下的能耗评价指标ζ，按照式(16)都除以最大操舵幅度下的能耗评价指标ζmax，得到能耗评价指标占比N1。同样，对表3中5.0 (°)/s操舵速率下，不同最大操舵幅度下的舵阻力能耗占比η，按照式(17)都除以最大操舵幅度下的舵阻力能耗占比ηmax，得到比值N2。然后按照式(18)计算两者的差异百分比，最终求取结果见表6。

(16)

(17)

(18)

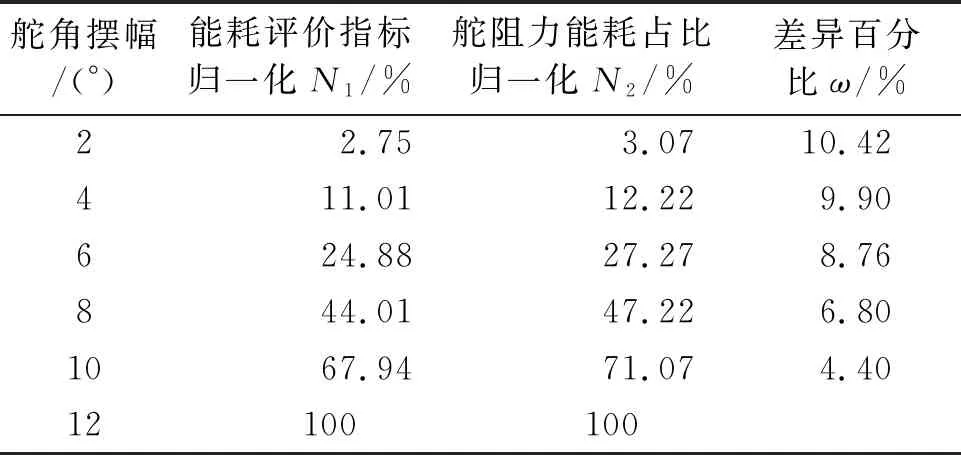
表6 能耗评价指标归一化验证

由表6可看出，同一操舵幅度下，归一化后的能耗评价指标与舵阻力能耗占比基本一致。相较于Nomoto和Motoyama提出的航向性能指标只有一个舵角平方项，本文提出的舵阻力能耗评价指标与舵阻力能耗间有更为明确的对应关系，能够反映出操舵仪在能耗控制方面的性能优劣。不同操舵仪在完成同一航行任务时，计算出的舵阻力能耗评价指标越小，则舵阻力能耗占总能耗比值越小，操控仪的性能越好。

4 结论

通过舵阻力能耗的理论求取公式的推导及周期性摆舵仿真试验，提出用于操舵仪性能评比的舵阻力能耗评价指标。周期性摆舵仿真试验结果表明，不同操舵方式将会带来舵阻力能耗的明显变化，所提出的舵阻力能耗评价指标与舵阻力能耗间有明确的对应关系，不同操舵仪在完成同一航行任务时，计算出的能耗评价指标越小，则舵阻力能耗占总能耗比值越小，操舵仪的性能越好。该指标与Nomoto和Motoyama提出的性能指标相比，计算更明确，应用范围更广。