用地质统计法优选煤田勘探程度的探讨

张 洪，张继平

（中煤科工集团沈阳设计研究院有限公司，辽宁沈阳 110015）

在煤田地质勘探中，有待查明的地质变量可分为区域化变量和标位变量。前者是对矿床某种特性的表征，它的取值既有随机性又有空间位置的实函数，如煤层的厚度、顶底板高程、含矸率、灰分、硫分、发热量等；后者是对地质体或区域化变量的位置、范围、界限、产状、形态等描述性变量。

为查明区域化变量而布设的钻探工程构成了煤田勘探的基本网度，同时要在基本网度的基础上再行布设辅助勘探工程，以完成对其搜索、定位与描述。现行的《煤、泥炭地质勘查规范》，以煤层赋存的稳定程度和构造的复杂程度定性的确定勘探类型[1]，并依此决定勘探网度与储量级别，不能定量地表示三者之间的关系，从而也就无法优选煤田勘探的基本网度。地质统计学用于储量计算和煤质预计，不但能给出最佳无偏估计量，而且能同时给出估计方差-估值的精度，这是此法的突出优点；这一估计方差是由勘探网度所决定的，即估计方差是勘探网度的函数。因此地质统计法为优选煤田勘探基本网度奠定了理论基础，它适用于赋存较为稳定、构造较为简单、产状缓倾斜或近水平条件的煤层。

1 地质统计法

1.1 区域变化量与半变差函数

地质统计法是以区域变化理论为基础，以变异函数为基本工具来研究那些展布于空间并呈现一定结构性和随机性的自然显现的科学[2]，把呈区域分布的既有随机性又有相关性的地质变量称作区域化变量。地质统计法在假设空间随机场平稳或内蕴的条件下，定义了地质变量空间分布规律的半变差函数。半变差函数是用于描述区域化变量规律、具有实用性的函数[3]，含义是相距h 的两点间区域化增量的方差的1/2。

1.2 克里格估值

克里格估值是一种求线性最优无偏内插估计量的方法，具体说，就是考虑了信息样品的形状、大小及其与待估块相互的空间分布位置等几何特征以及品味的空间结构之后，为了达到线性无偏和最小估计方差的估计，而对每一样品分别赋予一定的权系数，最后进行加权平均来估计块段品味的方法[4]。在已经建立的理论半变差函数曲线的基础上，以局部估计的方法求出各个待估点（或块）的最佳线性无偏估计量。

克里格方差是由于离开样品自身去推断它邻近点上取值而产生，因而它是一种外延方差（样品不等权条件下），因此，若干个样品S 估计块段V 的方差公式如下：

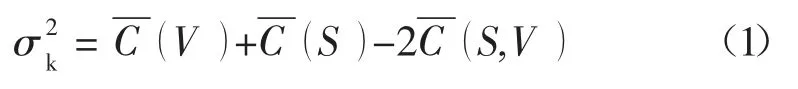
2 实例分析

依据上述地质统计学的基本原理，可用变换网度、网形的方法在计算机上模拟煤田勘探不同阶段网度由疏而密的勘探过程，求得克里格方差由大而小的相应变化，建立估计标准差、勘探工作量与网度、网形的关系曲线，依此优选基本网度、储量（煤质）保证率等[5]。

以胜利一号露天煤矿的煤田地质勘探资料评价专题报告[6]中5 煤厚度、5 煤含矸厚、6 煤厚度3 个变量为实例，对煤田地质勘探网度、储量保证率和储量备用系数进行模拟。

2.1 煤田地质勘探网度

2.2.1 勘探网度模拟

用地质统计法优选煤田勘探基本网度，一般为2 种方法：①平均估计标准差与勘探钻孔数D（一定网型下的孔数）关系曲线；②控制程度系数钻孔数D 关系曲线为平均厚度。且将2 种方法结合起来考虑。勘探模拟以正方形勘探网（简称方网）为基本网形，辅以十字花网（简称花网），不同网型网度的标准差及控制程度系数见表1。

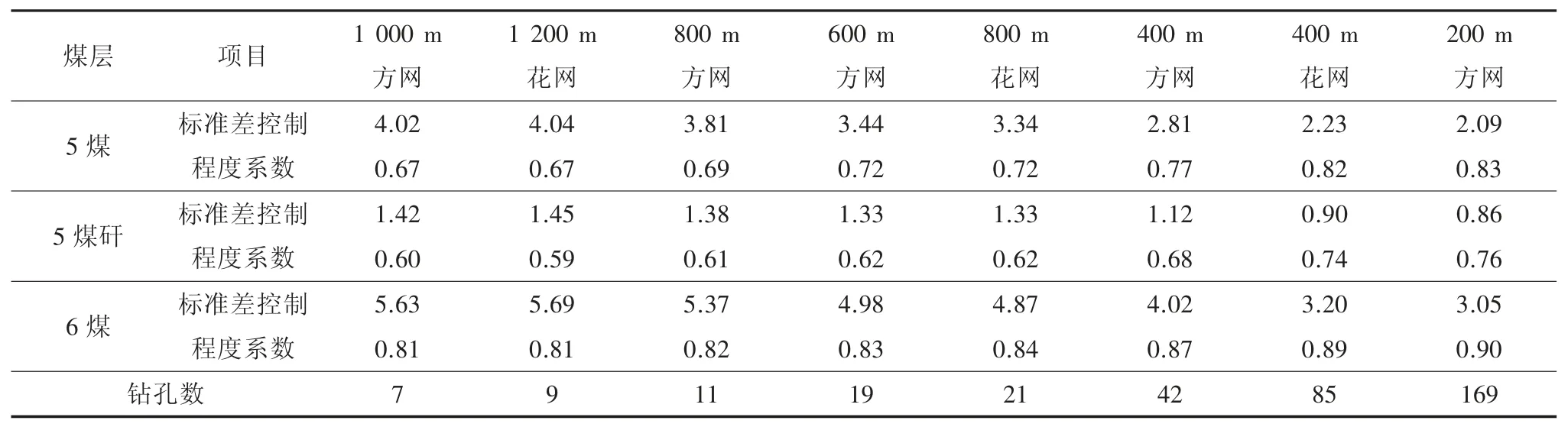
表1 不同网型网度的标准差及控制程度系数

以平均估计标准差σ 作为该网型下的估计精度指标，以6 煤为例绘出各模拟变量σ-D 关系曲线，6煤模拟变量标准差与钻孔数D 的关系曲线图如图1。露天矿全区L（L 为网度）关系曲线如图2。

图1 6 煤模拟变量标准差与钻孔数D 的关系曲线图

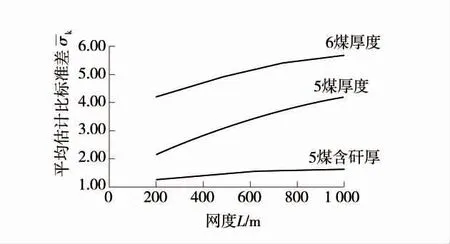
图2 露天矿全区-L 关系曲线

2.1.2 勘探网度优化

在2 种曲线上找出曲线率明显变小段，决定此段的钻孔数所对应的网度即是优选网度。它意味着在此网度（或勘探工程量）下，再增加工程量（加密网度）其勘探程度亦不再有显著提高，这种选择是符合经济合理费效比原则的。

从理论上说，优选勘探网度是个多目标决策问题，决定优选网度的主要因素可归结为勘探投资和勘探效益，因此可以用煤田勘探的费用和效益比例（费效比）对基本网度进行优选。特定义增孔效益F，表示由某一网度在增加1 个钻孔的储量增益，公式如下：

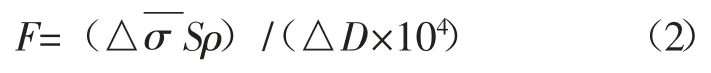
式中：F 为增孔效益，104t；△为勘探模拟中每相邻2 种网度下平均估计标准差的差值，如i网度时有i，i＋1 网度时有△，则△＝△σ-△σi；S 为模拟煤团的面积，m2，ρ 为煤层密度，t/m3；△D为i 网度时的钻孔数Di与i＋1 的网度时钻孔Di+1的差值，即△D＝Di+1-Di。

增孔效益本身具有费效比的含义。因为随着网度的加密由大变小，一般估值的统计分布是正态分布或近于正态的，所以随网度由疏而密的过程，正态分布曲线也由宽变窄。一般认为曲线由陡变缓的部位所对应的横坐标即为最佳勘探网度（即勘探所需的钻孔数），将计算的结果与实际勘探网度下的标准差对比，就可以了解勘探过程对矿床的实际控制程度[7]。显然，用这一指标去确定最佳网度应能获得较好的效果，但目前还不能确定出一个临界的最低增孔效益，用以衡量勘探程度，确定最佳网度。优选勘探见表2。

由表2 可知，优选网度5 煤厚为400 m 方形网，其余2 个地质变量均以400 m 花网为优，理论钻孔间距为283 m×283 m，实际上可近似地视为孔距300 m。优选网度的控制程度系数均在0.7 以上，6 煤的厚均在0.9 以上。

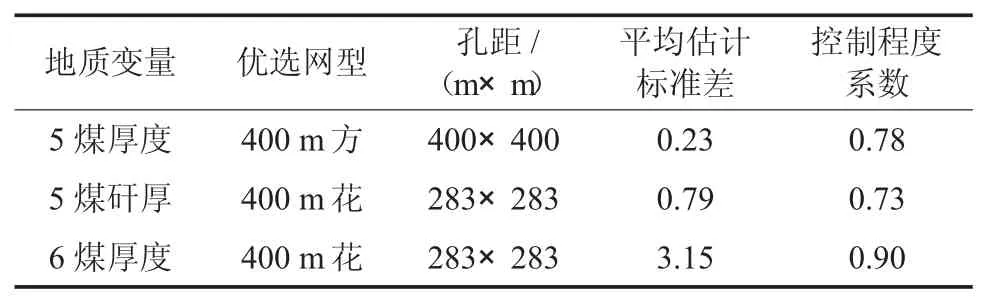
表2 优选勘探网型

从5 煤与6 煤的厚上看，5 煤的厚变化大，控制程度系数为0.78；5 煤含矸厚变化更强，在优选网型400 m 花时的控制程度系数为0.73。将勘探报告中各级储量网度与5、6 煤层优选网度进行比较可知：优选网度对应A 级储量。而地质报告中A 级储量区包括了一号露天煤矿全区的加密勘探网度[8]，孔距为400～200 m；5 煤、6 煤的优选孔距为400～300 m。

比较结果可知：地质勘探报告中的A 级储量区（包括加密勘探区）的勘探工程布置已满足优选网度的要求，在首采区的200 m×200 m 网度则已超过优选网度的标准。

2.2 储量保证率

储量保证率为大于等于某储量的可能性大小，即大于等于某给定储量的概率值。具体计算过程：

1）计算正态分布插表值u。

2）用u 值查正态分布函数表，从而得出概率P。

3）计算拟采用煤厚mi的保证率P（mi）。

4）此P（mi）即是相应储量的保证率。

2.3 储量备用系数

储量备用系数为：

式中：α 为储量备用系数，α≥1；m 为煤层厚度；X 为通过正态分布函数求出积分上限；为克里格估计标准差。

采用上述方法计算，胜利一号露天矿南部首采区储量保证率与备用系数见表3。储量备用系数1.10 条件下的储量及保证率见表4。

从表4 可知，一号露天煤矿拉沟区和南部区保证率在65 %～76 %，资源可靠，完全满足露天可研和初步设计的要求；而一号露天矿全区和东部首采区保证率在60 %以上，资源较可靠，能够满足可研设计要求。

表3 胜利一号露天矿南部首采区储量保证率与备用系数

表4 储量备用系数1.10 条件下的储量及保证率

3 结语

1）基于地质统计学原理，通过计算机的煤田勘探模拟，得了出煤田勘探控制程度（勘探精度）、煤田划定区域储量（煤质）的勘探优化网度、储量保证率和储量备用系数等指标。

2）通过勘探模拟建立起不同的网度、网形下勘探工程量与获得的煤炭储量（或煤质）精度之间的定量关系，找到了煤层稳定性、勘探网度、储量级别之间的定量关系。后者是煤炭资源勘探规范的重要课题，这种优选网度的研究最终可能导致勘探规范的修改和勘探程序的变更。

3）优选网度是在求得煤层变异性规律的数学模型-理论半变差函数-基础上用计算机模拟勘探过程而得出来的，优选网度还不是最佳网度，可以用煤田勘探的临界费效比（如前已提及到的最低增孔效益）选择最佳网度。它的实践意义在于：在煤田勘探的精查阶段，可用优选基本网度作为精查勘探设计依据，据此布置勘探工程，节省不必要的工作量，预测精查勘探的控制程度。在精查结束后，在用精查最终数据进行复算，检验控制程度，为精查勘探报告提供勘探网度合理性与勘探控制程度的定量论证。

4）勘探模拟方法-是一种单因素的优选法，因此在实际应用时，应该在正确地估计影响煤田勘探程度的主要因素的前提下，对其几个主要因数（如煤厚、煤质指标）分别优选，综合分析选择基本网度。若煤田有多个可采煤层，应对主要可采煤层逐个优选，综合分析选择基本网度。