基于贝叶斯网络的两栖车辆海上航行安全评估研究

宋 超，罗建华

(中国人民解放军陆军装甲兵学院，北京 100072)

0 引言

随着技术的飞速发展，人们对两栖车辆探索研究从未停止过，并勇敢付诸于实践。在第二次世界大战期间，Trippel[1]制造了一种两栖作战车辆，该车辆主要由装有Volkswagon行走机构的带轮子的浴缸组成，这是世界上首辆两栖汽车。随着不断大胆设计与实践，汽车制造商吉布斯(Gibbs)设计并完成了一辆名为Aquada[2]的两栖汽车成功横渡英吉利海峡，在水上可达到48 km/h的速度。随着两栖车辆的发展，两栖车辆在海上航行安全成为关注的问题。对两栖车辆海上航行数据结合其他船舶行驶数据以及安全管理中的事故进行分析研究，发现这种变化本质上是从事故定性分析和安全性向风险定量分析转变的结果[3]。船舶交通中的定量风险分析[4](QRA)是研究中最重要的问题之一。

风险具有随机不确定性。在模型不确定的情况下，当存在几种可能的模型来描述现象时，可以通过分配模型权重(每个模型正确的概率)并综合所有模型的影响，使用贝叶斯方法来包括所有候选模型。当有观测数据可用时，可以更新模型并将其转移到更合适的模型。此方法已应用于统计中的概率分布类型的不确定性和线性回归模型不确定性问题，并且最近用于解决机械模型不确定性。在这里，事故被视为是显而易见的，是描述该域的一些或全部随机变量的实例化。因此，随着人工智能的发展，可以使用统计学习方法来实现QRA。学习概率模型的方法(主要是网络推理)可以存储和调用特定实例。本文在分析两栖车辆海上航行系统风险影响因素的基础上，利用贝叶斯统计和网络学习方法建立了两栖车辆海上航行系统的风险评估模型。以期为两栖车辆海上安全航行提供参考。

1 两栖车辆海上航行风险评估模型

1.1 QRA模型

当涉及事件发生的不确定性时，风险定义为可能导致损失的系统故障的可能性。因此，此时风险涉及到两个因素，即事件发生的可能性和事件发生引起的潜在后果。Ayyub[5]提出了以下等式方程，使用可能性和后果因子评估风险。

Risk(Occurence,Consequence,Time)=Likelihood

(1)

在式(1)中，Risk可用于表示两栖车辆海上航行风险，Likelihood表示相关事件的概率或频率，而Impact则代表事件发生的结果。分析Likelihood(或频率)需要在所定义的特定事件发生概率(或在假设相关事件发生的频率)层面上建立特定状态(Ω,Θ,C)。

假设风险Rj(x,y,t)导致特定事故或事件的发生，其中可能的影响范围C是一个区域Ω，它覆盖一个平面区域Θ。在事故或事件发生时，由于发生事件而对平面范围内某个目标造成潜在危险的风险Rj(x,y,t)应符合式(2)：

(2)

式中，x，y表示风险中2-D位置特征，而t表示风险中时间特征，时间特征为3-D因子。

例如，两栖车辆海上航行系统中的某种危险Rj(x,y,t)导致了两栖车辆海上航行发生事故i，通常可以将其分类为交通事故组(碰撞，搁浅，接触等)。Pij表示由危险j引起i发生的可能性，而Cij(x,y,t)表示危险j与事故i之间的因果关系。

Pi的计算一直是风险管理研究的主要课题。可以使用历史数据，数学模型和专家判断来获得适当的可能性。

1.2 两栖车辆海上航行主观因素风险评估指标分析

两栖车辆在海上航驶过程中，车辆航行速度随着驾驶员的操作不断改变，两栖车辆在海上航行时类似于快艇，驾驶员需要熟练的快艇驾驶操作以及通晓水上情况[6]。在良好的驾驶操作下，两栖车辆海上行驶速度应为稳定的，急加速和急减速会给航行带来一定的风险。有时航道虽宽，但可能会遇到礁石，急加速、急减速可能会引起交通事故。由此，加速度为影响两栖车辆海上航行安全因素。对两栖车辆航行加速度进行分析，根据数据可得加速度随时间变化规律如图1所示。

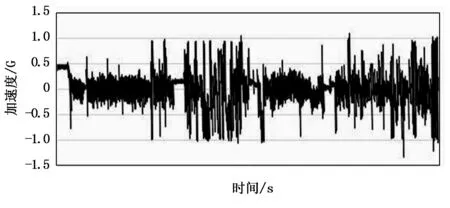
图1 加速度随时间变化规律

如图1所示，两栖车辆在航行开始时加速度是一个相对稳定状态；在良好的驾驶操作下，包括航行、制动、停车等阶段，加速度应为平稳上升或下降；急加速和急减速都为不良驾驶操作，在航行过程中，会引发海上交通事故。利用SPSS对加速度随时间的变化进行研究分析，结果如图2所示，直方图分析如表1所示。

表1 加速度特征值分析

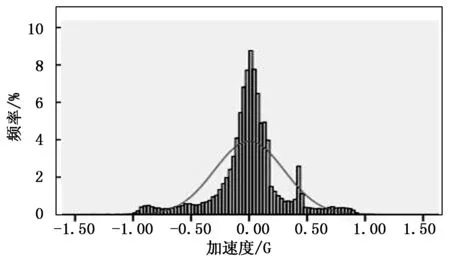
图2 加速度直方图

百分位/%加速度/G百分位/%加速度/G5-0.583 178 71600.044 921 8810-0.330 078 13700.089 355 4720-0.142 089 84750.120 117 1930-0.069 824 22800.149 414 0640-0.025 878 91900.368 652 3450-0.011 230 47950.485 351 56

根据概率划定加速度对应安全等级，表3所示。

表3 不同加速度安全等级表

2 贝叶斯方法

贝叶斯理论在人工智能(AI)的大多数研究领域都取得了巨大的成就，其中包括因果关系的推论，不确定性的描述、模式的识别和聚类分析。这些成果已被引入到最近的风险分析研究中[7]。

2.1 叶斯可能性点估计

假设样本集A1,A2,…，An构成一个完整且独立的总体Θ。Ai(i∈[1,n]是E中发生的事件，而B中的事件指的是一个已发生事件，其中P(B)≠0。由此得出结论，贝叶斯规则的公式可以由式(3)表示：

(3)

当事件发生概率符合以下方程式时，对于事件Aj，则离散随机参数θ可定义为θ=θj=Aj(j=1,2,...n)，式(4)：

π(θj)=P(θ=θj)=P(Aj),j=1,2,…n

(4)

因此，{π(θj),j=1,2,...n}构成随机变量的先验概率分布。该概率可通过历史统计数据或对事件概率的主观判断来计算推导出来。通常可以通过以下3种方法确定先验概率。

假设X是与B相关的离散随机变量，则符合以下方程(5)：

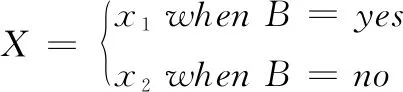
(5)

从式(1)中可以推导出发生B条件下的后验概率(或条件概率)，如式(6)所示：

(6)

此时，概率分布{π(θi|x1,i=1,2,...n}可以看作是在样本X下的{π(θi),i=1,2,...n}的概率分布。

2.2 叶斯网络结构学习

贝叶斯网络(BN)用于以某种方式下对包含不确定性的域进行建模[8]。贝叶斯网络原称为因果概率网络。BN是有向无环图(DAG)，其中每个节点代表一个随机变量。每个节点都包含它所表示随机变量的状态以及条件概率表(CPT)，即条件概率函数(CPF)。给定其父节点的状态，节点的CPT包含该节点处于特定状态的概率。各字符、字母所代表含义如下。

假设随机变量集X和代表网络结构不确定性的离散变量θ，其中可能网络的催眠度为Sh，先验概率为P(Sh)。在随机样本D的条件下，其后验概率为P(Sh|D)，如式(7)所示：

(7)

其中：P(D)为归一化常数。

常用的贝叶斯学习方法是朴素贝叶斯学习器，通常称为朴素贝叶斯分类器。贝叶斯学习中最常用的网络模型为朴素贝叶斯模型。在此模型中，类变量X是根，属性变量A是叶。在属性值为a1,a2,…，am的情况下，每个类别的可能性由等式(8)给出：

(8)

在给定描述实例的值的情况下，贝叶斯对新实例进行分类的方法为对目标值做最可能的分配，即VMAP。VMAP计算公式如式(9)：

(9)

将其代入式(10)，我们得到了朴素贝叶斯分类器所使用的方法。

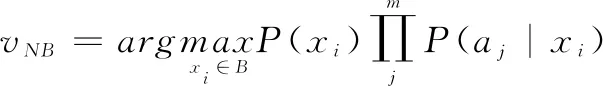
其中：VNB表示目标值输出。

该等式可以等效地表示为使ln最大化，即使该数量的负数最小。

(11)

2.3 贝叶斯参数学习

给出了贝叶斯网络的结构，并且试图学习该参数[9]。迄今止，已经根据观察到的事件在机会总数中所占的几分之一来估计了概率。为避免困难，本文采用贝叶斯方法，使用定义如式(12)的m估计来估计概率。

(12)

在此，将n定义为发生xi的训练例的总数，nc是发生aj的训练例的总数。p是我们希望确定的概率的先前估计值，而m是样本大小常数。

3 两栖车辆海上航行风险的贝叶斯网络分析

两栖车辆海上航行交通是一种由车主、两栖车辆、信息和环境组成的两栖车辆操作系统[4]，也可以通过将其分为主观因素和客观因素来进行分析。系统的物理特征可以表示为贝叶斯信念网络[10]，其中将这些特征视为样本。

3.1 两栖车辆海上航行可能性的贝叶斯估计

本文将历史数据引入目标先验概率的计算中。实验中统计事故数量用以描述事故发生的频率，它可以作为风险评估的客观标准，也是系统安全性仿真研究中的关键参数。两栖车辆海上航行交通事故是随机事件，符合两栖车辆海上航行流量的二项式分布。事故统计定律可以用概率分布的数字特征(均值，偏差，变化)来描述。根据事故统计，当有足够的统计间隔或事故样本时，两栖车辆海上航行系统中事故样本的分布函数满足式(13)：

(13)

参数θ具有以下等式(14)的先验分布:

(14)

此外，两栖车辆航行系统中事故的后验分布满足以下方程(15)：

(15)

该公式描述了k个两栖车辆活动中k次事故的概率。后验分布满足方程(16)的等式：

(16)

同时，相关参数符合方程组(17)：

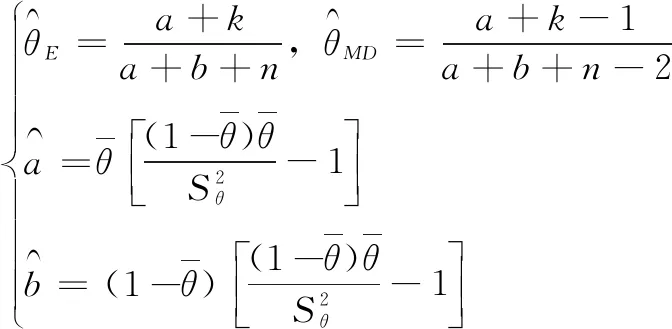
(17)

3.2 两栖车辆航行中的统计样本

在QRA中，危害识别(HazID)是一项艰巨的工作。但是，概率影响图可能对此很有用。通常，两栖车辆导航系统由4个因素组成，即软件，硬件，软件和环境，其中包括两栖车辆交通风险，两栖车辆运动，水路，航道和引航模式。系统中的所有功能都可以视为离散且独立的证据。例如，“国家”一词用于表达航行水域包括国内，海外和公海的特征。

贝叶斯网络模型是通过拓扑构造的。每个节点可以用以下表达式说明：

A0 =<非常，严重，少，轻，安全>

A1 =<国内，海外，公海>

A2 =<正在航行，靠泊，锚泊，转向系泊，不系泊且沿船，离港船>

A3=<海洋，“航道”港口，海岸，锚地，捕鱼区>

(18)

A4=<引水，非引水>

A5=<雾，重海，正常>

A6=<碰撞，接触，激流，火，浪，其他>

3.3 两栖车辆航行中的风险评估

计算两栖车辆导航系统中物理特征的概率，以找出特定时间段内两栖车辆安全行驶的总体和内部情况及趋势，以及把握风险的特定特征，这一点在两栖车辆行驶过程中至关重要。对实施提高两栖车辆行驶安全性的详细措施，分析系统的因果关系，评估当前的安全状况以及寻找事件的缺陷和事件等具有重要意义。因此，贝叶斯概率法可有效地计算两栖车辆行驶中的风险。

3.3.1 两栖车辆航行事故概率估计

由于两栖车辆发生航行事故数据量较少，且两栖车辆在海上航行时类似于游艇航行，文中将游艇事故数据添加其中，丰富两栖车辆数据信息。事故发生概率可基于近年来的两栖车辆和游艇航行事故发生频率来进行两栖车辆和游艇航行事故发生的概率。例如，表4展示了近年来发生的两栖车辆和游艇航行事故。

表4 近年来发生的两栖车辆和游艇航行事故

根据第四部分中的贝叶斯统计，交通中的概率符合式(19)：

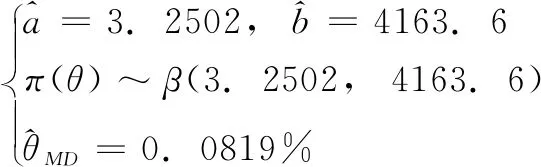
(19)

3.3.2 两栖车辆航行事故样本结构

可以通过使用历史数据，数学模型和专家判断来获得适当的概率。本文通过2006年至2019年的统计事故建立了事故样本结构。所有样本都将被描述为物理特征，例如天气，运动，水路，航道和引航模式。

贝叶斯学习后，贝叶斯信念网络可以显示如图3所示。

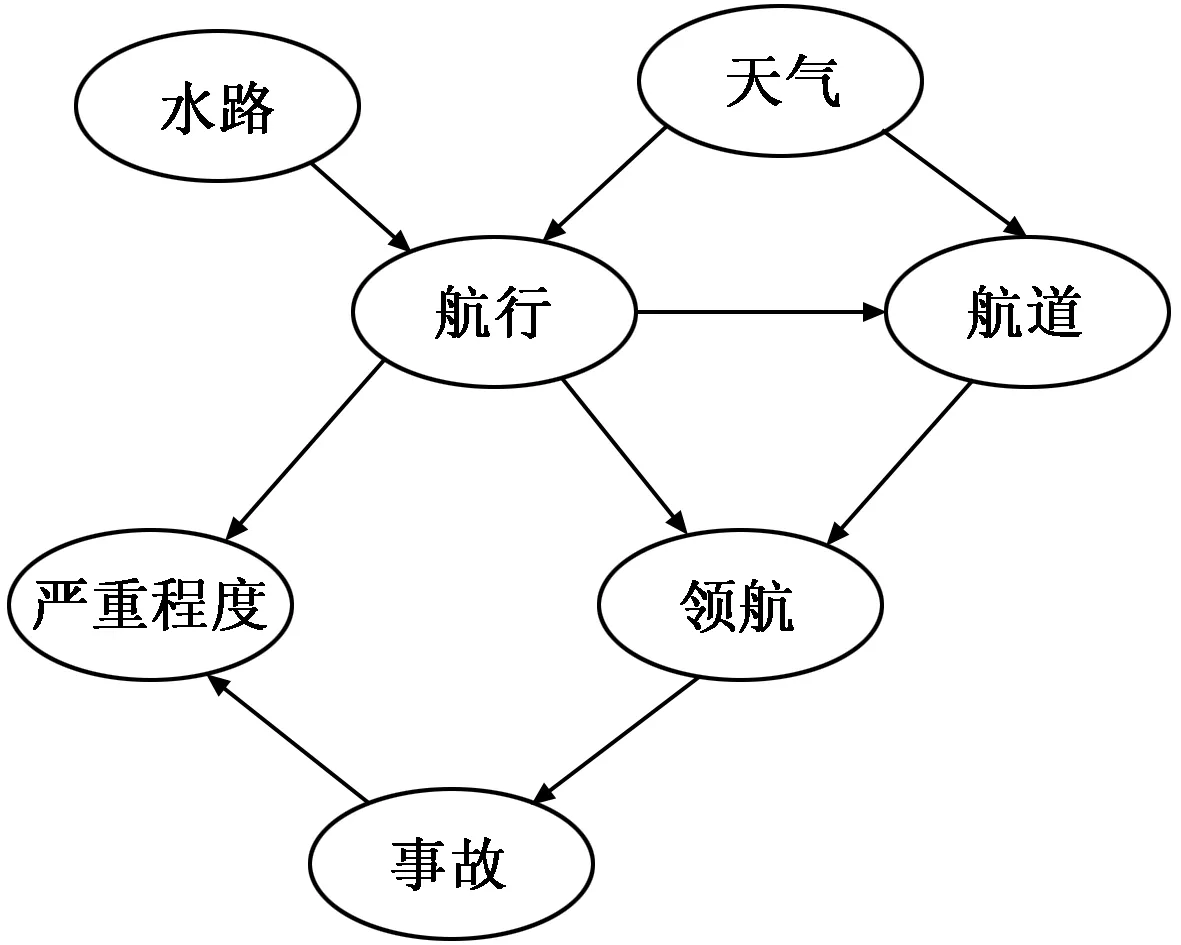
图3 贝叶斯信念网络

3.3.3 两栖车辆航行事故参数学习

基于第三节中的计算，可以在出现严重不利的条件下推导出各特征Pj(θ|A1,A2,A3,A4)的条件概率。如果严重性等级可以量化[11]，则可以根据以下等式(20)计算各种特征的条件概率下的风险：

(20)

其中:wi表示Pj下严重程度的分布。

根据相关文献[7，12-13]，结合图4，上述结果分析如下：

图4 贝叶斯网络学习

对于在A1，A2航道中的两栖车辆航行，较高的风险主要存在于国内航道的航行中，其次是在海外航道的航行中，最后是在海外航道的停泊中。

对于运行中的航道A2，A3，以下区域构成更大的风险：民航航道，海外航道的港口以及海外航道的沿海地区。而海外水道的航道紧随其后，同样构成较大风险。

至于领航水区A1，A3，A4中的两栖车辆航行，主要风险在于航道—领航—航行，其次是沿海地区—非引航—航行以及港口—非引航—航行，第三是航道—非引航—航行，港口—引航—靠泊，以及港口—非引航—靠泊。

对两栖车辆航行构成相对风险的多种功能A1，A2，A3，A4的综合分析，高风险区域的规模按降序排列如下：1)航道—引航—国内水道—航行；2)沿海地区—非引航区—国家水道—航行。

4 结束语

两栖车辆航行安全的讨论一直是两栖车辆研发、运行的重要问题。为了确保两栖车辆安全航行，已经做了很多工作。本文在对主观因素如加速度和客观因素如航道、天气等因素对两栖车辆海上航行安全进行建模分析，在贝叶斯概率统计和网络推理的基础上，进行系统风险分布的定量计算分析，得到两栖车辆海上航行安全估计结果，并在QRA案例中得到了验证，为其海上航行提供有利的建议。