基于BP神经网络的天平校准数据处理方法研究

车兵辉，尹欣繁，彭先敏，章贵川

(中国空气动力研究与发展中心，四川 绵阳 621000)

0 引言

天平是用于风洞试验中的具有多分量的力传感器，在使用之前必须对其进行校准和标定，获取其计算公式。天平的静校是在实验室内模拟天平使用时的受力状态，通过在各分量上单独加载或组合加载不同的载荷，获取天平的对应输出电压值，然后通过插值拟合、解方程等方法获取输入和输出量之间的对应函数。目前普遍采用线性插值拟合的方法获取天平公式[1]，然而多分量天平各分量之间存在干扰，在拟合公式是要考虑干扰项，通常二次干扰和组合干扰会出现非线性特性，采用线性拟合方法会产生较大误差。

神经网络具有很强的非线性映射和泛化功能，能够较好地描述非线性系统和不确定系统。目前神经网络在多领域获得了极其广泛的应用，尤其是BP网络，即反向传播网络，使用最为广泛。BP网络是利用非线性可微分函数进行权值训练的多层网络，在函数逼近、多维插值、模式识别等领域得到广泛应用[2]。在系统辨识、传感器非线性修正、传感器校准等方面也有广泛应用。多分量天平是一个典型的多变量传感器，输入输出关系是一个典型的多输入多输出系统，因此本文针对多分量天平的特点，采用BP神经网络算法对多分量天平公式拟合方法进行研究，通过算例验证此方法的应用效果。

1 BP神经网络

1.1 BP网络结构

BP网络(Back-Propagation Network)又称反向传播神经网络，是一种多层的前馈神经网络，他是一种具有3层或3层以上的神经网络，由输入层、中间层、输出层组成，中间层可以是1个也可以是多个，典型的3层网络结构如图1所示，信号从输入层进入顺序经过中间层节点处理，最后传到输出节点，同一层内节点互不相连，且每一层节点都与相邻层所有节点相连，因此每一层节点只对下一层节点产生影响[3-6]。其主要的特点是：信号是前向传播的，而误差是反向传播的。

图1 典型的3层网络结构

BP网络采用的传递函数是非线性变换函数——Sigmoid函数(又称S函数)，即：

(1)

式中，xi为神经网络中第i个输入，wij为前一层节点i至该层节点j之间的权值，输出层传递函数为线性传递函数。

由于BP网络采用误差梯度最快下降法，在计算误差梯度时需要对传递函数求偏导，S函数本身及其导数都是连续的，因而在处理上十分方便。

1.2 BP网络算法原理

BP网络学习算法的基本原理是梯度最速下降法，他的主要思想是调整网络连接权值,使网络总误差最小，也就是采用梯度搜索原理，寻找合适的连接权值，使网络的实际输出值与期望输出至误差均方差最小。网络的学习过程是一种误差不断向后传播不断修正权系数的过程。这种学习过程以一种训练过程，是网络各神经元连接方式、连接权值和阈值的调整寻优过程，更是参数辨识过程。学习的方法是使误差达到设定值，从而获得输入输出数据之间的关系。

BP网络所有的连接权值和阈值都可以通过学习调节。多层网络学习过程包含正向和反向传播两个阶段，第一阶段是信号的前向传播，输入信息从输入层经过中间层逐层处理，并传到输出层，每层神经元的输出只影响下一层神经元的状态。如果输出层不能得到期望输出，则进入第二阶段反向传播，误差信号从输出层到中间层，最后到输入层，依次调节中间层到输出层的权重和阈值，输入层到中间层的权重和阈值。重复以上两个阶段，直到系统整体误差最小。

根据以上分析，多层BP网络学习的具体过程和步骤如下：

1)初始化参数，给权值和阀值赋予(0,1)区间的随机数。

2)选取一组输入和目标样本。

3)用输入样本、权值、阀值逐层计算输出值，并与期望目标比较，当误差满足时结束，否则进行下一步。

4)根据误差修正权值和阀值，公式如下：

(2)

其中：v为中间层至输出层连接权值，w为输入层至中间层的连接权值，γ和θ分别是输出层阀值和中间层阀值，d为输出层各节点误差，b为中间层节点输出，e为中间层各节点误差，x为输入层节点输入，λ和β为学习参数，取之范围为(0,1)区间。

5)返回步骤2)重复，直到所有样本学习完为止。

网络训练完成后可以获得v，w，γ，θ参数的值，则网络可表示为：

(3)

式中,N为中间层节点数，Fi(i=1，…，6)为输出信号，g为输出层节点传递函数，f为中间层节点传递函数，Sm(m=1，…，6)为输入信号。根据上式即可计算出给定输入值对应的输出值。

2 天平校准数据处理方法

2.1 多项式拟合方法

天平的静校是在实验室内模拟天平使用时的受力状态，对天平施加静态载荷，通过静校求出天平使用公式、精度和准度[7]。

天平加载得到一组施加载荷和相应的电压值输出，设Fi(i=1，…，6表示6个分量)为加载的载荷，Si(i=1，…，6表示6个分量)为输出电压值，则天平公式可表示为：

(4)

式中,ai，bi，…，fi(i=1…27)分别为Fi(i=1…6)分量的27个校准参数。以上关系建立在参数ai，bi，…，fi(i=1…27)为线性条件下，加载载荷Fi和电压输出值Si(i=1…6)为已知量，参数ai，bi，…，fi通过曲线拟合获得[8-9]。

将上式简写为：

[F]=[K][S]

(5)

则系数矩阵[K]可表示为：

[K]=[[S]T[S]]-1[S]T[F]

(6)

根据上式可计算出天平公式中的系数矩阵，从而获得天平计算公式。

以上分析是建立在系数矩阵为线性的，如果系数矩阵具有非线性特性，通过上述方法拟合出的计算公式会有较大的误差。

2.2 BP神经网络拟合方法

天平校准是根据加载已知载荷作为天平系统的输入，获得的各分量应变计输出电压为输出。天平系统模型是载荷到电压值之间的映射关系，然而在使用时天平所加载的载荷是未知数，可获取的是各分量应变计电压值，需要根据电压值求取载荷值，因此需要获取电压值到载荷值之间的映射关系，是天平系统模型的反函数，天平公式的拟合就是求取天平系统模型的反函数，图2给出了天平公式拟合原理。

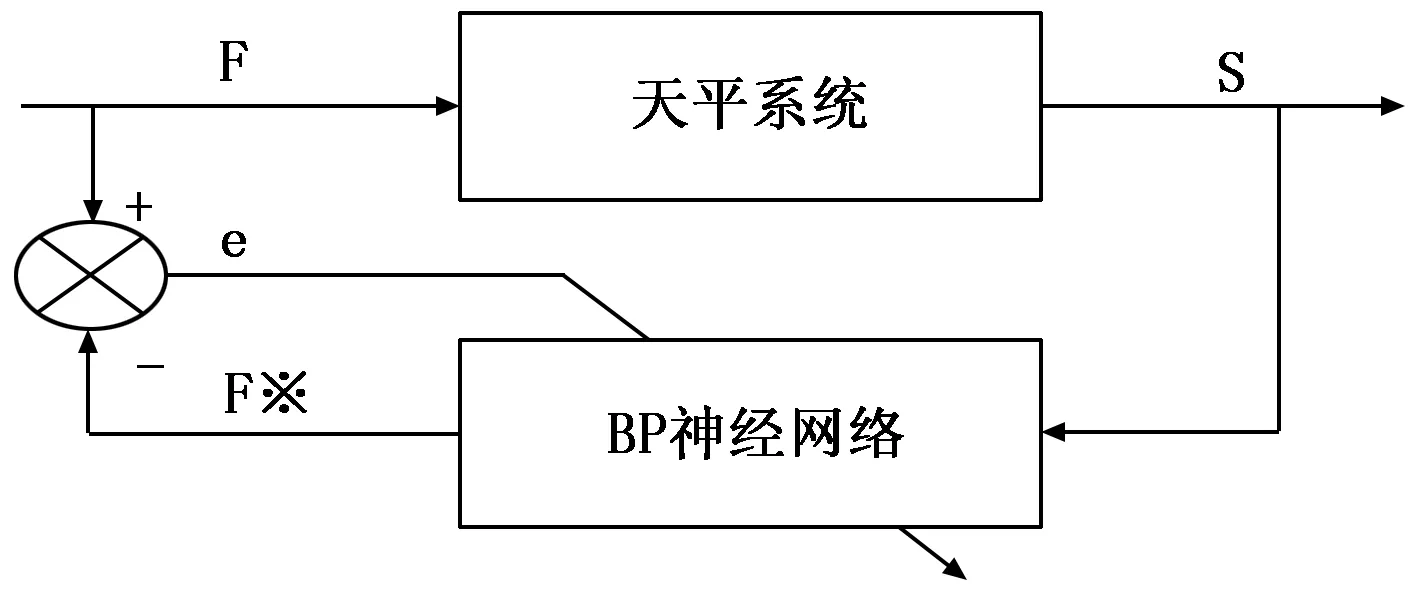
图2 天平公式拟合原理

根据BP神经网络具有极强的输入-输出非线性映射能力的特点，以天平校准获得的各分量应变计输出电压值数据集Si(i=1…6)为输入样本，对应的加载载荷Fi(i=1…6)为输出样本，对神经网络进行训练，逐层计算输出，并与目标值比较，获取误差e，根据误差修正各层权重矩阵，使得拟合误差满足要求，完成训练过程，得到各层的连接权重矩阵。在使用时，根据获得的天平各分量的电压值，采用式(3)即可计算出对应的载荷值。

BP神经网络中间层节点数可自由设定，研究表明一个三层网络可实现以任意精度近似任何连续函数。因此采用BP神经网络作为天平公式模型是可行的。神经网络训练时加载输入端的数据太大，会使参数收敛速度慢。此外，由于在神经网络中采用S型函数，输出范围为[0，1]，因此在神经网络训练前对数据进行变换，使其在区间[0，1]，变换公式如下：

(7)

式中,xi为输入或输出数据，xmin为数据样本中的最小值，xmax为数据样本中的最大值。

建立神经网络天平公式模型的步骤如下:

1)获取天平校准原始数据。表1给出了天平校准时的部分加载载荷数据(各分量的最大、最小值和零载荷)，每个分量的加载载荷在量程范围内等间隔选取，六各分量共计81个样本，表2给出了对应的天平输出电压值。

表1 部分典型加载载荷 kg、kg·m

2)由式(7)将原始数据进行归一化，得到训练神经网络的输入输出样本。

3)确定神经网络输入输出端数量、各层节点输、λ和β的值。网络输入端数量与输入层节点数量相同，输出端数量与输出层节点数相同，均等于天平的份量个数(一般为6)。中间层节点数根据拟合精度确定，精度要求高时，取较大值，反之亦然。中间层数量、λ和β的值的确定需要结合精度要求、训练效果等确定。根据所确定的输入输出数量建立的网络结构如图1所示。

4)将训练样本输入构建好的网络进行训练，直到达到要求的精度为止，保存获得的连接权重和阈值。

5)将获得的连接权重和阈值带入式(3)即可获得天平载荷计算公式。

3 神经网络方法实现及应用

采用c语言实现BP神经网络的训练，将训练样本读入程序，实现自动学习，并保存训练后的结果。

3.1 神经网络算法实现

根据第1节中描述的BP神经网络训练步骤编写程序，图3给出了软件实现的流程图。

首先建立网络数据结构并初始化变量，网络数据结构如下：

typedef struct BPNet{

int LayerNum;//中间层数量

double **v;//中间层权矩阵

double **w;//输出层权矩阵

double StudyRate;//学习率

double *bi;//中间层阀值

double *bo;//输出层阀值

double Accuracy;//精度控制参数

int MaxLoop;//最大循环次数

}BPNet;

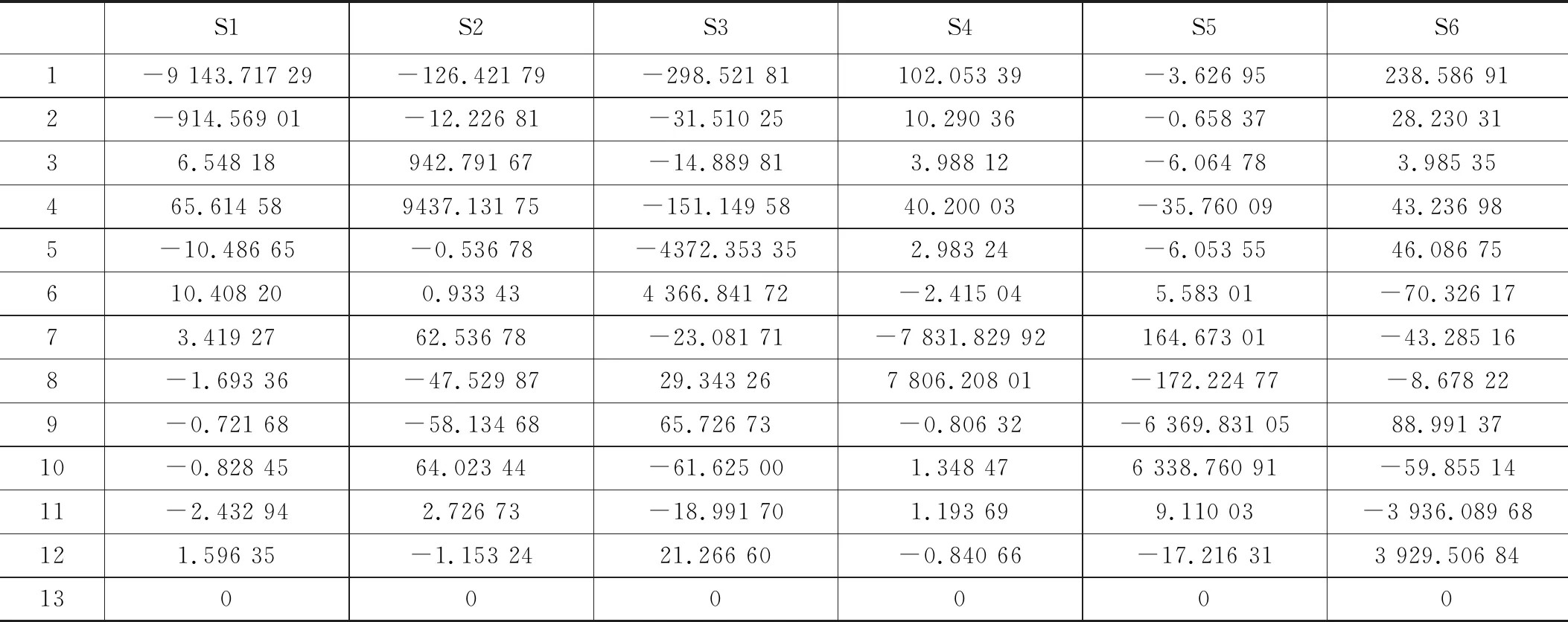
表2 对应的天平输出电压值(单位：10 μV)

图3 软件实现的流程图

变量主要有中间层权重矩阵V和阈值bi、输出层权重矩阵W和阈值bo，其中V为m×n的二维数组，W为n×r的二维数组，bi为n个元素的一维数组，bo为r个元素一维数组，m为输入层个数，n为中间层个数，r为输出层个数。将这些变量初始化为(0，1)范围内的随机数。

训练过程实现如下：

读取样本并根据式(7)归一化样本数据，初始化学习率StudyRate、精度Accuracy等参数；

E=0；//初始化误差

While E>Accuracy do

{

For i=1 to SamplesNumber

{

For k=1 to n//计算中间层输出

{

}

For t=1 to r//计算输出层输出

{

}

计算输出误差e；

按照式(2)修正权重矩阵和阀值；

}

E=E+e；

}

保存得到的权值矩阵和阀值向量；

训练结束。

3.2 神经网络方法应用

采用某天平的校准数据，共81个样本。选用以下参数对网络进行训练:输入层节点数6，分别为天平6个分量(3个力和3个力矩)的电压值，中间层节点数为10，输出层节点数6，分别为天平6个分量的载荷，学习率λ和β取0.001，目标精度0.001。将样本归一化后输入网络，神经网络学习16 700次达到精度要求，图4给出了训练收敛特性。

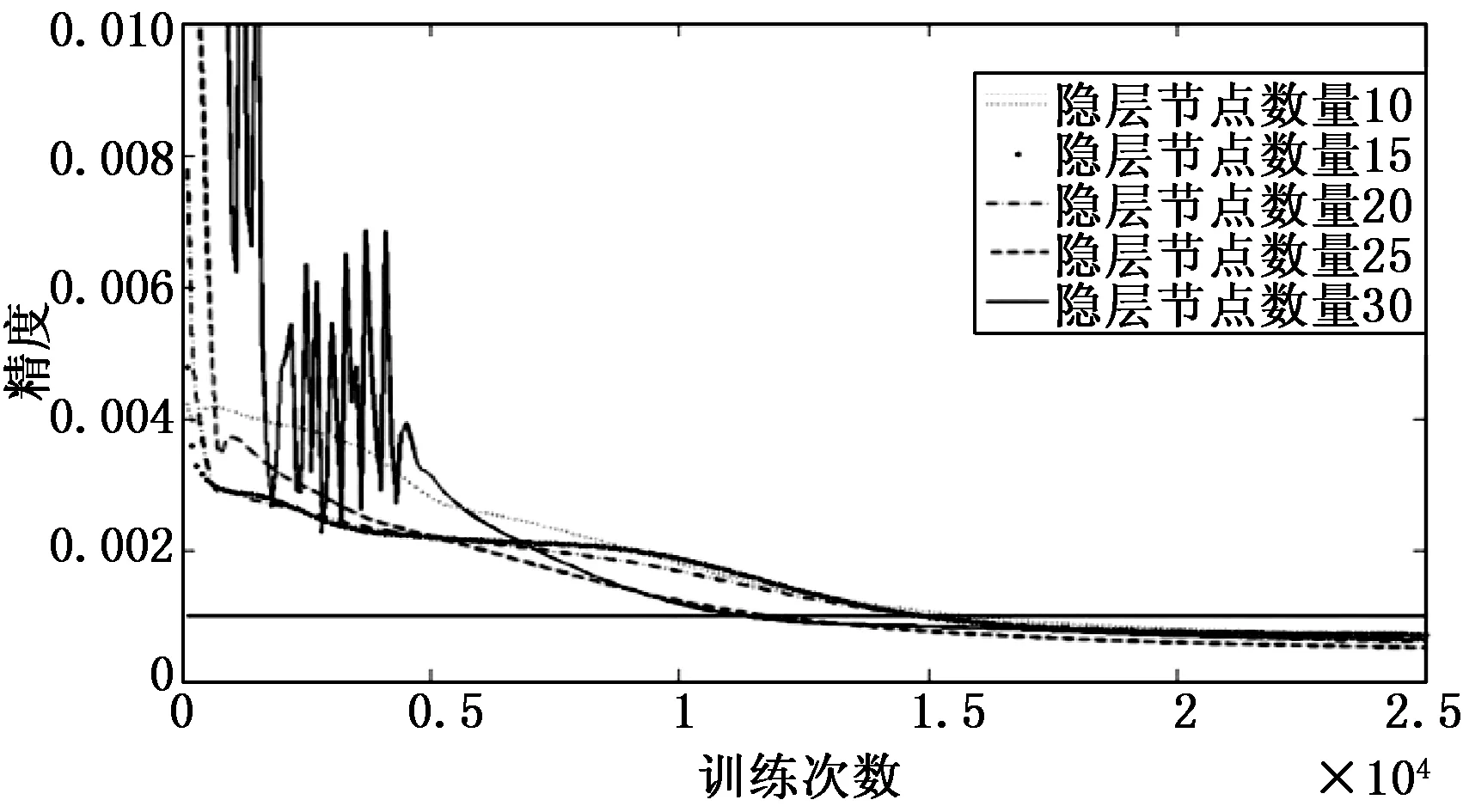
图4 训练收敛特性

从图中可以看出训练过程能够很好地收敛，训练次数越多精度越高，增加训练次数可近一步提高训练精度。中间层的节点数关系到网络的训练性能，图中也给出了中间层节点数为15、20、30时的收敛特性，节点数增加时收敛速度会加快，当节点数为30时过程中出现波动，收敛速度的没有明显变化，因此节点数的选择不是越大越好，对于输入向量数较少的网络中间层数量不宜选择过大，需根据训练结果综合考虑。

为了检验神经网络的训练效果，选取训练样本中的一部分作为检验样本，将输入值进行归一化后，根据式(3)计算电压值对应的载荷值，通过网络计算出的载荷值为归一化后的数据，要获取实际载荷值，需要采用训练时的归一化参数进行反归一化，反归一化公式如下：

(8)

图5 两种方法计算的误差

4 结束语

本文通过对天平校准数据的处理和公式拟合方法进行了研究，提出了BP神经网络的拟合方法，建立了基于神经网络的天平输入输出模型，通过校准数据对模型进行训练。这种方法充分利用了神经网路的非线性特性、学习能力，通过样本训练逼近系统的输入输出特性，有效地克服了系统的非线性误差。结果表明，采用神经网络模型的天平公式拟合和采用多项式拟合方法相比，天平公式的计算精度平均提高了67%，取得了很好的效果。该方法为天平或其他多变量传感器的校准提供了新的思路。