基于回归模型的全卷积网络人群计数算法

吴晓燕

(四川文理学院 智能制造学院，四川 达州 635000)

0 引 言

人群密度估计在现实生活中的需求量很大，是公共安全、交通监控等一系列实际应用中的重要参考信息[1,2]。现有的人群计数方法大致可以分为3类[3]，即基于检测的方法、基于回归的方法以及混合方法。早期的人群计数工作[4]中主要使用基于检测的方法，这类方法主要是基于事先定义好的头部检测器对图像进行处理。但是，当人群密集度高或者严重遮挡时，该方法的估计准确率明显下降。基于回归的方法[5]旨在学习人群计数和特定特征之间的直接映射，可以完成较为复杂环境下的人群计数问题。目前常用的回归模型有高斯过程回归、线性回归以及神经网络等。

随着深度学习的快速发展，神经网络逐渐应用于人群计数方面。Li等[6]应用条件生成对抗网络进行回归估计人群规模，取得较好的结果。Xiong等[7]提出了一种深度学习模型convLSTM，用于捕获空间和时间依赖性，提高人群计数的准确性。Saqib等[8]在深度卷积网络框架的基础上，引入运动引导滤波器来监测视频中的人群数量。Liu等[9]提出了一个深度递归空间感知网络，通过设计空间感知优化模块和采用动态地定位人群密度图中注意力区域的方式，自适应解决图像中人群尺度和旋转问题。文献[10]提出了一种CSRNET网络用来提高人群密度的估计精度。文献[11]通过结合欧几里得损失和计数损失来约束SANET网络，并使用一组转置卷积创建高分辨率密度图。文献[12] 在深度卷积网络的框架中编码人流统计的语义性质，然后结合行人、头部及其上下文结构进行群体计数。

当前大多数方法均采用单一的密度图回归估计人群数量，但是在估计过程中容易产生人数被高估的现象。针对这一问题，本文提出一种回归模型，通过计数回归与密度图回归相结合的方式解决上述问题，并采用更深更轻的完全卷积网络(full convolutional network，FCN)作为人群密度图估计器，使得模型参数数量很少。

1 全卷积网络

全卷积网络是在卷积神经网络CNN的基础上，将VGG-16模型中的全连接层全部改为卷积层，使其可以接受任意尺寸的输入图像。FCN是对图像中的各个像素进行分类，在输出端得到每个像素所属的类。然后利用反卷积操作对最终获得的特征映射进行上采样，通过放大操作使处理后的图像尺寸与输入图像尺寸相同。在这个过程中，不仅可以保留原始输入图像中的空间信息，还能够对特征图内的每个像素做出预测，进而实现逐像素分类。图1给出了CNN和FCN的结构对比图。

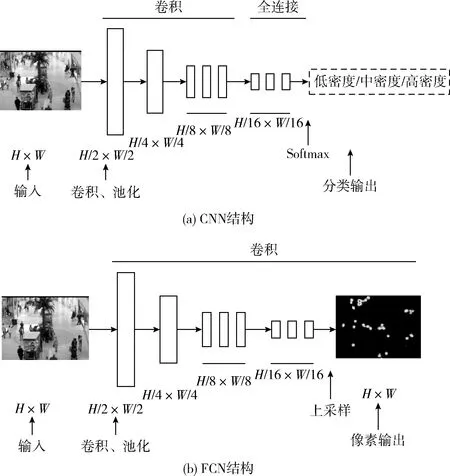
图1 CNN和FCN的结构对比

FCN可以分为FCN-8s、FCN-16s和FCN-32s 这3种模型，反卷积实质上是将不同卷积层和池化层的上采样结果求和，然后利用反向传播算法对网络进行端对端的训练。相对于经典的CNN模型，全卷积网络的优点有：

(1)卷积层参数少于全连接层，有效降低过拟合现象的出现；

(2)全卷积网络特征图中的像素只需提取其对应的图像感受野内的信息，不需要提取全图信息，减少了无关背景的干扰；

(3)全卷积网络能够适应不同尺寸的输入图像，应用更广。

2 基于全卷积网络的人群规模估计算法

2.1 基于回归模型的全卷积网络

本文采用的FCN的架构如图2所示，该模型分为编码、译码和输出3部分。编码部分有3个阶段，每个阶段由两个卷积层和一个最大池层组成。卷积层的内核大小、步长和填充分别设置为3、1和1。最大池层的内核大小和步长都设置为2。在解码部分，也有3个阶段，每个阶段由一个卷积层和一个反卷积层组成。利用卷积层来减少特征映射的数目，因此设置特征映射的核大小和步长为1。为了对特征映射进行升序，卷积层的内核大小、步长和填充分别设置为4、2和1。解码阶段的特征映射将与编码阶段的特征映射连接起来，以重用低级特征。

图2 本文采用的FCN的架构

2.2 代价函数

使用基于回归的方法进行计数有两种方式：一种方法是通过训练一个模型，直接从给定的图像中输出头部数量估计；另一种方法是输出人群密度图，通过对密度图进行积分，获得人群的头部计数。由于密度图能够给出人群的空间分布，而且模型容易训练，因此更多的研究采用第二种方法。但是，如果训练参数、学习率、批量大小等参数设置不恰当时，密度图上的人数通常会被高估。为了解决这一问题，本文采用密度图回归和计数回归相结合的方式进行人群估计，训练结构如图3所示。

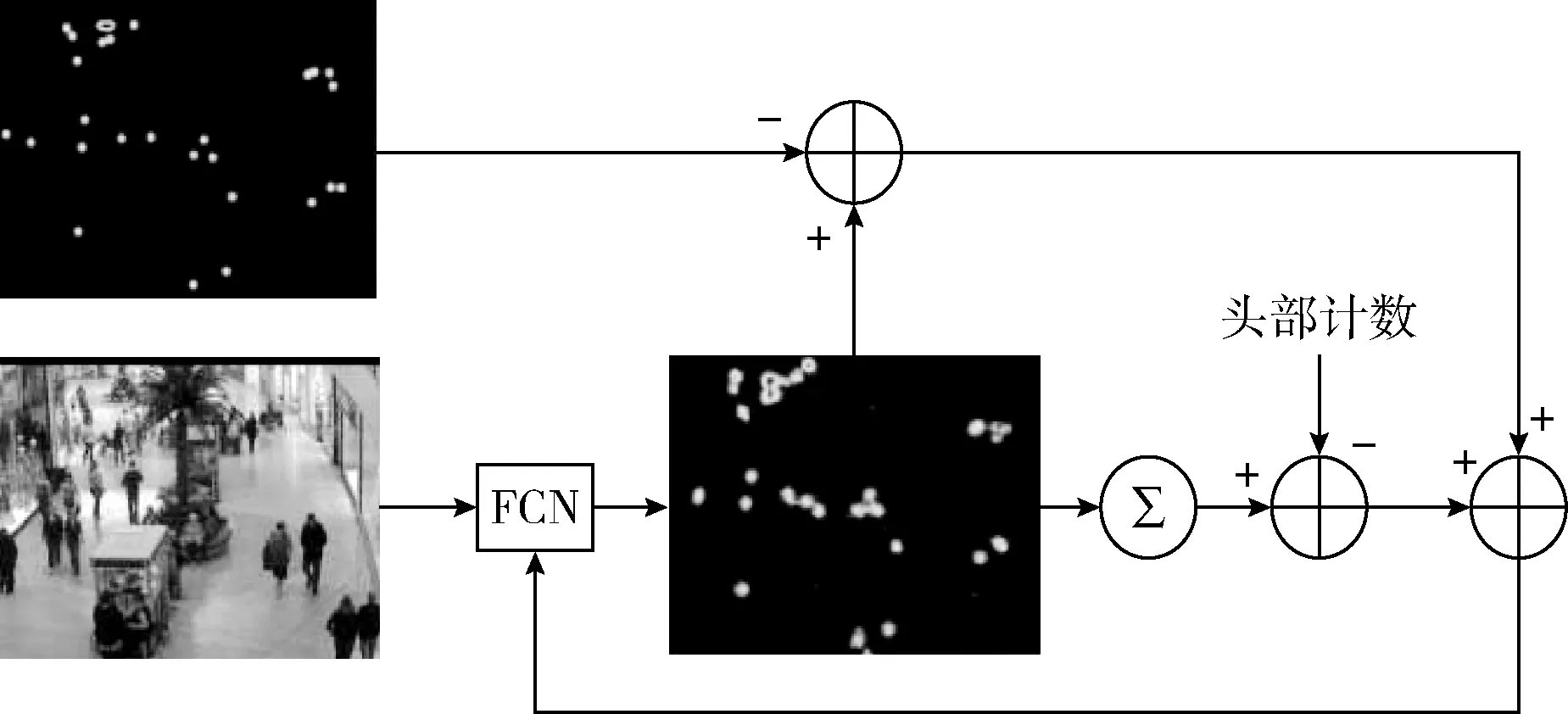
图3 基于密度图和计数回归的人群估计

头部模型为二维高斯分布，因此，人群密度函数可写为

(1)

其中，x是密度图上的位置，Ni是第i张人群图像上的头部数量，μi,j是第i个人群图像上第j个头部的位置，σ是高斯分布的标准差。密度图回归的目的是训练一个模型，将输入人群图像Hi(x)转换为密度图，所以密度图回归的代价函数可以表示为

(2)

其中，NF为训练图像片段的个数，S为人群图像片段上的位置空间，Fi表示第i个人群图像片段。M(x,Fi|W)是参数为W的人群密度图估计模型，通过最小化式(2)，该模型将能够根据输入的人群图像片段估计密度图。

由于来自训练模型的密度图可能会导致对头部数量的高估，本文采用计数回归方法对模型的输出值进行正则化，然后对Hi(x)进行积分，可以估计出输入图像的总人数。通过缩小头部数量估计值和真实值之间的差异来规范密度图估计。计数回归的代价函数表示为

(3)

结合密度图回归和计数回归的总的代价函数为

E(W)=αED(W)+βEC(W)

(4)

其中，α和β是用来规范化训练的超参数。

在训练前，该模型不能估计人群密度图。如果直接应用计数回归，训练损失很难收敛，因此需要对模型进行逐步训练。首先，利用密度图回归对模型进行训练。在模型能够很好地估计密度图后，再加入计数回归模型。由于密度图回归的误差是每个像素上所有误差的积分，导致它比计数回归的误差大很多。因此，超参数α在设置时应该小于β，故(α,β)在第二次和第三次的设置分别为(0.1,10)、(0.1,100)。

3 实验结果与分析

3.1 评价标准

为了测试提出算法的性能表现，分别利用均方根误差RMSE、平均绝对误差MAE以及出错率ER对测试结果进行评估，3个评价标准的定义如下

(5)

(6)

(7)

3.2 数据集

采用Mall[8]数据集、UCSD[10]数据集以及WorldExpo′10[11]数据集来测试所提出算法的性能，同时与现在一些最新算法进行对比。实验过程中，Mall数据集、UCSD数据集和WorldExpo′10数据集使用标准训练和测试分割方式进行测试。为了防止网络过拟合，在训练集上进行了数据增加操作：训练图像通过镜像来增加图像数量。为了增加头部大小的可变性，在构建图像金字塔时，本文采用比例系数γ∈[0.6,1.2]乘以原始图像分辨率，步长为0.2。Mall数据集由购物中心内可公开访问的监控摄像头捕获，图像的照明条件和玻璃表面反射对算法具有很大的挑战性。该数据集是一组2000帧的视频序列，前800帧进行训练，剩余的1200帧用于测试。UCSD数据集是户外监控摄像机拍摄的图像数据，主要分成两个子集，子集1有34个训练视频和36个测试视频，每个视频有200帧，子集1有10个训练视频和16个测试视频，每个视频有120帧。WorldExpo′10数据集由来自108个不同监控摄像机捕获的1132个视频序列的3980个带注释的帧组成。该数据集分为来自5个不同场景的训练集(3380帧)和测试集(600帧)。表1显示了两个数据集的各种统计结果。

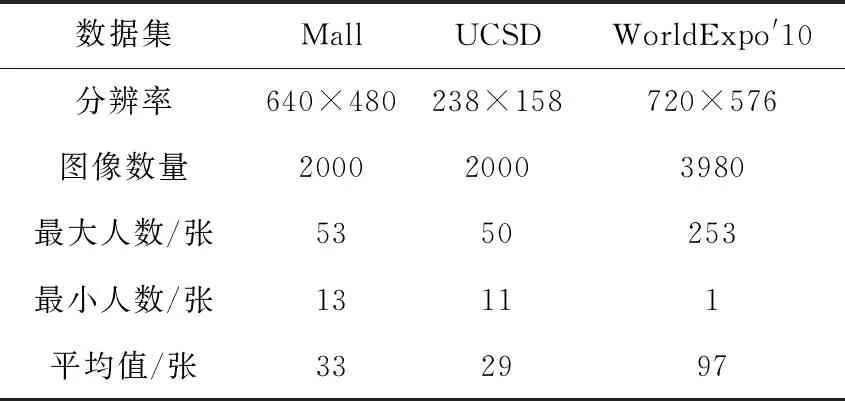
表1 两个数据集的统计结果

3.3 实验结果与分析

图4给出了本文算法在3个数据集中测试的视觉效果。本文算法在人群密度中等场景的WorldExpo′10数据集、人群密度小但分布变化很大的场景Mall、UCSD数据集以及上表现良好，从而充分说明提出算法的准确性和适用性。

图4 3个数据集的预测和真实密度图对比

图5、图6给出了不同算法在Mall和UCSD两个数据集在MAE、RMSE的实验结果。通过对比每个数据集上不同算法的测试结果，发现在Mall数据集和UCSD数据集上，提出的模型优于其它方法。

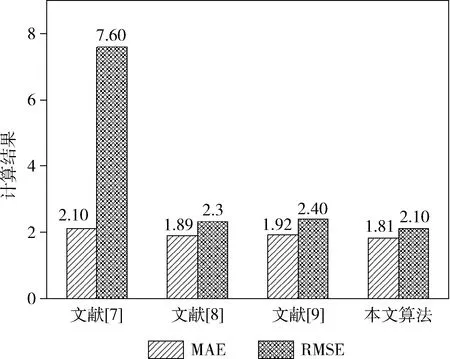
图5 不同算法在Mall数据集的测试结果

图6 不同算法在UCSD数据集的测试结果

图7给出了不同算法在WorldExpo′10数据不同场景的MAE测试结果。本文模型除了场景4的测试结果不如文献[12]，其余场景及平均值均优于其它算法。

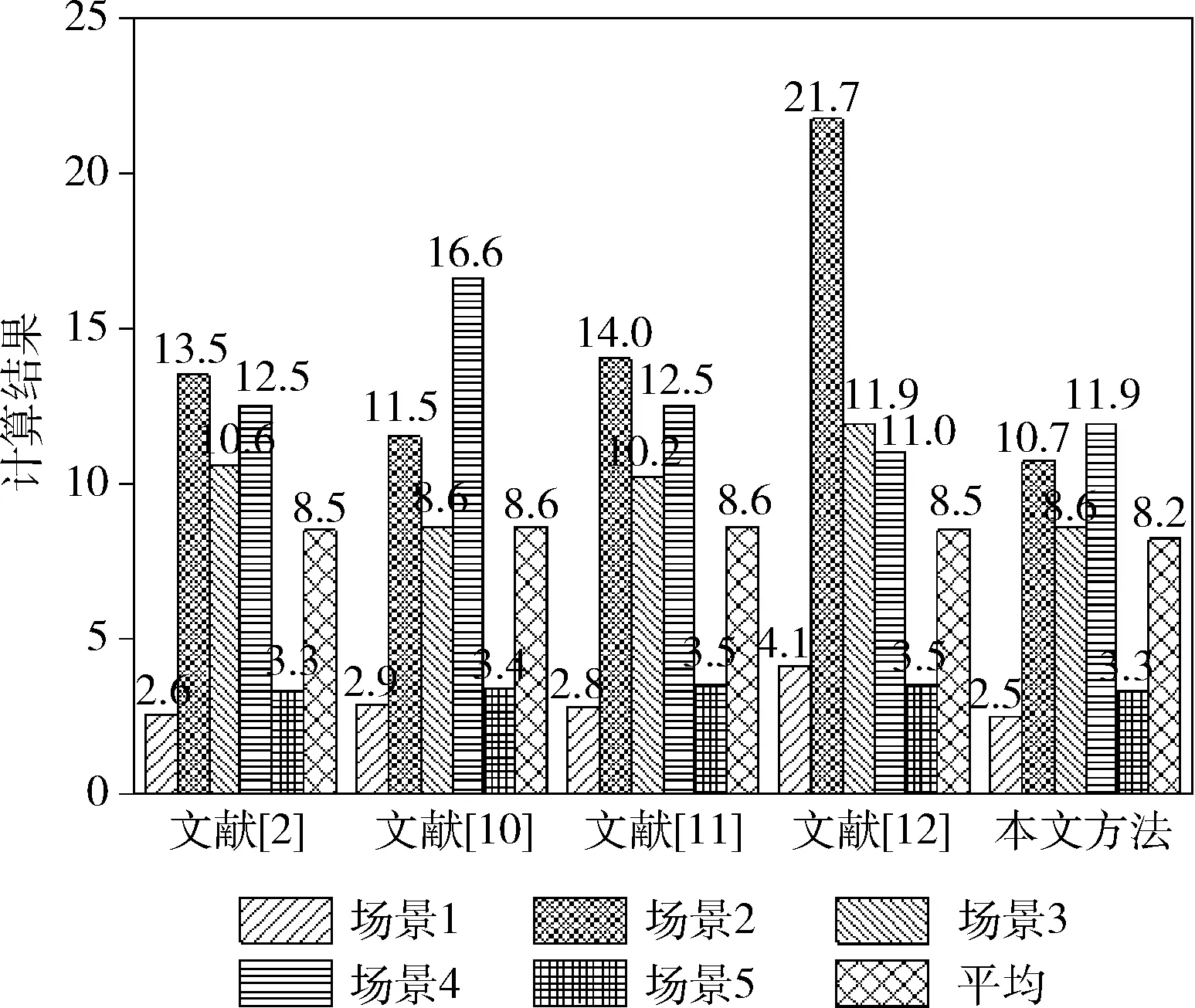
图7 不同算法在WorldExpo′10数据集的测试结果

图8给出了不同算法的累积误差。从图中可以看出，随着图像数量的增加，每种方法的累积误差将被累积，累积误差线的斜率越低，性能越好。除此之外，通过对比每个数据集上不同算法的测试结果，本文方法的累积误差最低，性能优于其它算法。

图8 不同算法的累积误差对比

4 结束语

为了纠正密度图回归方法估计人群数量过高的问题，本文设计了一个更深的、更轻的且参数数量很少的人群计数FCN模型，采用将密度图回归与计数回归相结合的方式估计人群密度。提出的方法在不同的人群密度和尺度不一的数据集上均取得了较好的效果，有效避免了仅通过密度图回归进行训练时总人数被高估现象的产生。实验结果表明，与其它现有的人群计数方法相比，本文模型计算精度更高，性能更优，训练策略也具有更强的竞争力。