基于邻域纹理的线段匹配方法及应用
胡丹青,吴绍锋,林靖宇
(广西大学 电气工程学院,广西 南宁 530004)
0 引 言
室外建筑测绘的信息数据量大,提高信息提取与融合过程自动化程度是目前测绘的发展方向。通过大量的图像信息库提供源数据,希望尽可能压缩数据降低运算量。建筑物的几何结构有点、线、面3种,点特征检测分布过于分散,而面特征提取多是近似为平行四边形。对建筑物运用线段特征进行描述研究,则可以折中地获得相较于点特征更小的位置信息描述数据量,从而缩短计算迭代的时间,并且线段上的元素相对关系具有更强的三维空间关联[1]。根据现阶段的线段特征研究主要有两个描述子发展方向:其一是通过线段上特定点元素匹配的方式,Shen Yan等[2]提出通过点特征将图像进行单应变换后匹配相应线段的方法,Kai Li等[3]提出通过找到线段交点的SIFT邻域匹配方法获得线段对。这类方法为了保证匹配的准确度,通常会保留较多用于计算的点特征的数据量,但还是逃不开点特征匹配过程中遮挡产生的故有问题,未能充分利用建筑的几何结构关系。另一类是基于线段基元本身的特性描述进行匹配的方法,Bart Verhagen等[4]提出将梯度描述子拓展到整个线段的匹配方法。Francesco Castaldo等[5]提出RGB图像的语义信息用于立体视觉的线段匹配。Hyunwoo Kim等[6]提出基于交叉线段归一化之后的相似性进行线段匹配。对线段邻域的梯度、颜色等特征的分析是利用了线段所处环境的特点增加匹配的信息,根据建筑物室外装饰形态的特点,提出纹理分析结合几何结构特点是很有必要的。
基于上述分析,本文提出一种基于邻域纹理相似度比较的直线匹配方法。通过线段邻域的纹理特征统计的差异,将建筑物同一平面上的相邻框架线段分成一组,对每一组线段生成包含纹理信息和结构位置信息的描述子,最后的评价函数通过巴氏距离比较纹理直方图相似度。
1 线段提取
采用Linelet算法[7]对建筑物图像进行直线提取,该方法对建筑物框架线段的提取连续度高、检出丢失率低。由于Linelet算法在检测自然界物体时也不会丢掉其中的线段特征,在图像中的草丛、树叶、树枝等接近线段特性的物体也会提取出线段基元,所以本文中的算法对线段提取结果设置的粗筛阈值,将占总检出数量半数以上的短线段剔除,这些短线段多数是从自然界的纹理特征中提取出来的,而建筑物主体结构的框架多是较长的连续线段,所取得的邻域范围与线段长度呈正相关,长线段可获得更多的描述邻域,故剔除短线段后可降低本文算法的计算时间和匹配误差。
在采集图像移动的过程中,目标建筑会出现尺度缩放的情况,为了克服图像缩放的问题,减小线段选取邻域时尺度变化引入的描述误差,对进行线段匹配的两幅图像搭建图像金字塔。本文采用3层图像金字塔处理,对每一层尺度空间上通过Linelet算法提取到的线段加上尺度空间和提取顺序两个标签进行标记,使得同一线段在不同尺度下相互关联。在进行线段匹配时对两个金字塔不同尺度之间进行组合比较,取各个尺度下的最佳匹配线段对。
2 线段描述子
2.1 邻域模型
纹理是一种有规律性的呈现于物体表面的特征[8],根据建筑物设计与装饰的特点,建筑物表面的装饰呈现出的纹理规律比自然界中的纹理规律性更强、周期更小,纹理相对于建筑结构的分布关系不会随着采集视角的变化而改变。本文基于这个特点对建筑物表面的线段进行匹配。
基于线段邻域的直方图统计方法,是将图像中提取到的线段特征分别取特定邻域,通过计算直方图的方法对这个邻域中像素分布的位置和像素值进行计算统计信息,并且把这个信息作为对应线段的特征描述子。一条线段的邻域纹理直方图可表示为
(1)
(2)
其中,T表示某一个区域的纹理统计直方图,对这一个区域的像素灰度值x从0到255分别统计得到一个统计向量h(x),Texture表示线段邻域统计直方图的完整描述信息,Tj与Ti分别表示两侧统计邻域区块的纹理,下标i,j∈part。
目标线段的描述邻域在两侧对称分布,其中一侧邻域为长度等于目标线段总长、宽度为W个像素的矩形区域,则一个邻域分区内的像素总数W×Member个,Member是每个区域长度的像素个数。每侧邻域沿目标线段的矢量方向均分为part个区块则每个区块就是一个纹理统计描述的最小单元,依次对part个区块的各个单元进行式(1)的邻域纹理直方图统计,则可以得到一个目标线段的邻域纹理描述子。线段邻域分区方法如图1所示。

图1 线段邻域分区方法
在没有考虑邻域像素与线段距离的情况下,同一个区块中各个像素对纹理统计直方图的影响因数是相等的。当增加邻域的宽度W以获得更多纹理信息时,随着区域宽度W的增加,各线段邻域内纹理的像素统计直方图区分度会逐渐缩小,匹配误差增大,当邻域取为整个图像时,一幅图像中各线段的描述差别为零。本算法在描述子中增加一个维度,即加入被统计的像素与线段的距离w,在沿线段的法线方向上,纹理像素的统计影响因子呈现高斯分布,这符合视觉认知的规律,即离中心越近的信息对判断的影响越大,像素影响因子的高斯分布系数方法如图2所示。以线段为中心w=0,两侧邻域纹理的直方统计占比为
(3)
其中,totalpixles表示线段邻域分区内纹理像素个数的总数,它等于邻域宽度乘分区线段基元的像素数即W×Member,pixles(x)表示当前区域像素灰度值为x∈[0,255]的像素个数,w为像素离中心线段的距离。采用式(3)的分区形式可以将不同长度的线段归一化为相同的分区数,进一步降低描述子对于线段长度的依赖,有助于在匹配过程中解决尺度变换带来的匹配问题。
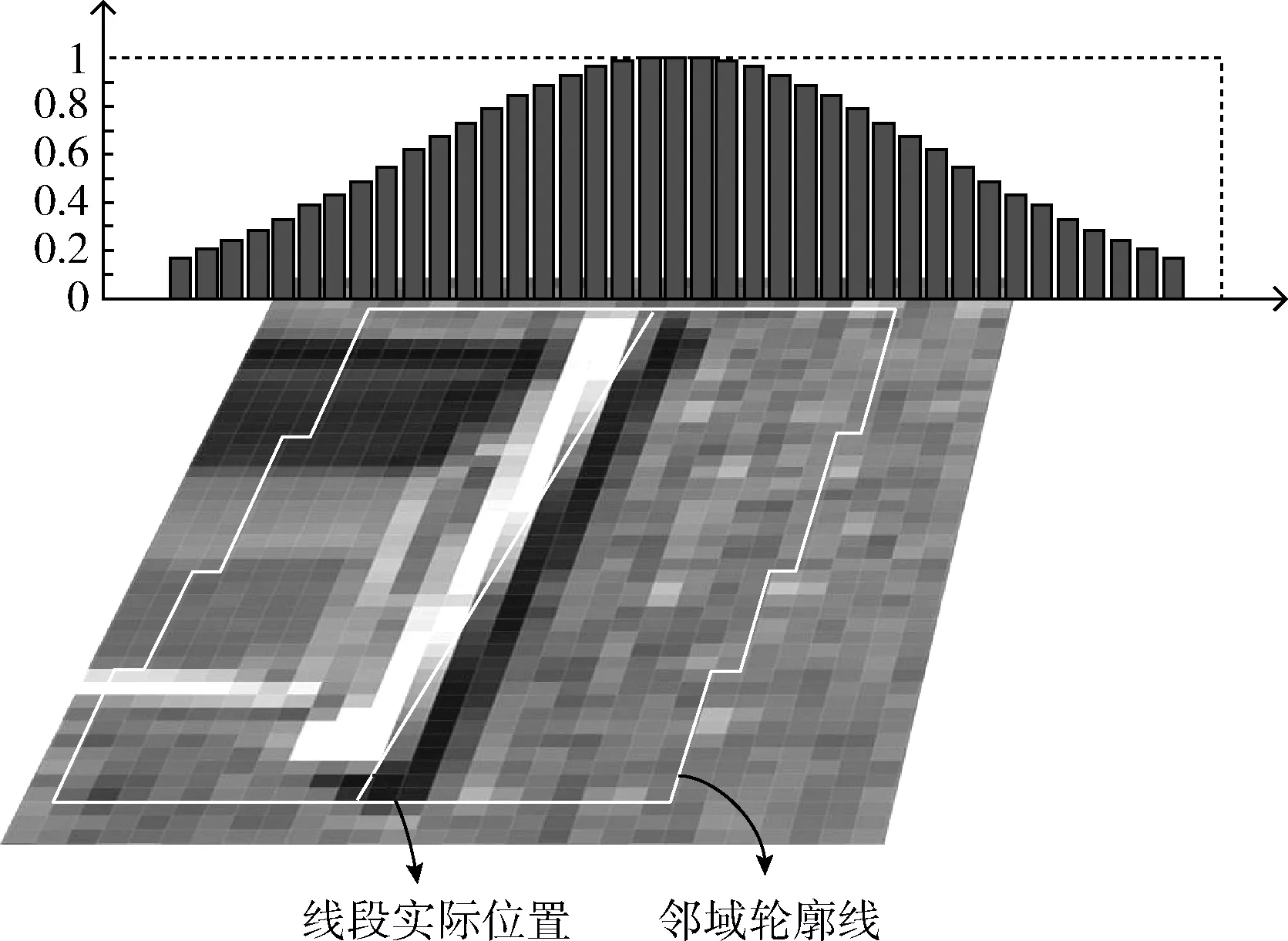
图2 线段邻域像素到中心距离与影响因子的关系
2.2 分组匹配模型
在图像拍过程中,若出现相机镜头旋转时,一条孤立的线段是无法确定正方向的,也就是说当相机旋转180°时,若按照图像的原始坐标确定线段的正方向,则会存在同一条线段由于两侧的纹理互换也会无法匹配。所以描述子中需要增加有效的描述线段角度的模型,保证线段匹配描述子具有旋转不变性。针对如何保证旋转不变性这个问题,本文提出了以下方法来解决。通过观察和分析建筑物表面框架结构发现,建筑物的框架是由线段相互组合相接形成的结构,三维空间中相交线段组的交点和线段组之间邻域的建筑物表面纹理特征是稳定的,不会随着图像旋转而变化。
利用鲁棒的周边线段组合的方法确定线段正方向,在图中检测到的线段集合中找出与目标线段夹角大于阈值τθ的k条线段{l1,l2,…,lk},将线段集中的每条线段分别与目标线段计算最近点之间的距离,找出最近点距离最小的线段,假设目标线段的两个端点分别为P1、P2,在k条线段集{l1,l2,…,lk}中存在端点分别为Q1和Q2的一条线段,线段P1P2和线段Q1Q2上分别有点P、Q可以如下表示
(4)
求解其目标函数min(P-Q)1/2可以得到线段上点的最近距离用于筛选目标线段的结构线段组,还可以得到两个端点到线段最近点的比例系数λa和λb,但这对比例系数在透视变换中不是完全不变的,所以设置了偏差范围τλ,用于辅助判断的线段匹配条件。
在得到满足最近点距离条件的线段后,比较线段和目标线段的夹角内侧的纹理统计直方图相似程度,若达到阈值且相似度最高的,则两条线段为同一平面的框架边界的可能性较大,通过组合的方法,将同一个平面上的相交或相邻的线段组合为具有夹角和正方向的线段特征描述单元。
2.3 纹理匹配的描述
通过将筛选内侧夹角纹理后的线段组作为最终构成描述线段匹配的组合单元,综合以上分析和计算过程中获得的信息,需要完整的包含纹理信息、夹角和正方向3个方面的描述,并且保留冗余筛选条件。依据线段组的关系属性,线段的描述子应该具备夹角内侧纹理、夹角两侧纹理、线段夹角度数、最近点所在线段比、线段组所在金字塔层数共6个元素
ARG={Tinside,Toutside,θ,θmid,λa,λb,N}
(5)
其中,Tinside表示当前线段组两条线段所夹平面的纹理直方统计特征。Toutside表示当前线段组所夹平面外侧的纹理直方统计特征,作为夹角外侧纹理情况的标志。θ表示线段组中两条线段在所夹平面一侧形成的夹角角度,θ∈(τθ,π)。θmid是两条线段夹角的中线与图像横坐标轴正方向夹角的角度,λa是组内两线段最近点在lP上的位置与端点的比例关系,λb是组内两线段最近点在lQ上的位置与端点的比例关系。N表示线段组所处在金字塔的层数。
描述子中的6个元素是根据描述子ARG中的排列顺序重要性依次递减,最核心的元素Tinside是本文算法中判断线段匹配的最基本依据。Toutside为线段外侧夹角纹理,若线段组为建筑物表面凸结构的平面的两条框边,如房顶拐角等,则外侧纹理在拍摄视角出现较大的变化时可能会存在变化。线段组成员之间的夹角θ要大于阈值τθ我们才认为它们是一组稳定的夹角,且有可能是建筑物的结构框架。前3个元素均具有缩放和旋转不变性,其余是作为冗余筛选条件。所以在进行图像之间线段组匹配比较时,也是依照描述子元素的排列顺序依次进行比较的。
完成线段组合之后,定义线段的正方向表示为从靠近交点的一侧端点指向线段上远离交点的一侧端点,则定义线段正方向后就可以定义线段夹角的内侧,即邻域纹理分区的标号沿线段定义的正方向依次增加,得到如线段邻域外侧纹理标记分区图3的邻域分布。线段组内侧邻域为两条线段正方向所夹,即若定义一条线段的正方向左侧为正、右侧为负,或上侧为正、下侧为负,则为了方便说明将两条线段旋转至如图中方向所示,一条平行于图像横坐标轴,内侧纹理分别处在两条线段的②和③处,只有在②和③的纹理比较相似度大于阈值的时候两条线段才可能被划分为一组,所以Tinside表示②和③的直方图相加。Toutside包含①和④两侧的纹理统计直方图以及①和②、③和④的纹理是否相同,相同标记为1,否则标记为0,会出现4种情况00、10、01、11,利用这4种情况作为记号先进性粗筛可以提高匹配的效率。

图3 线段邻域外侧纹理标记分区
引入针对建筑物结构描述的线段分组方法,从线段进一步提升至相交线段组成的平面上的纹理,通过线段维度与建筑物表面纹理特性的组合, 加强了建筑物结构上的线段位置与线段邻域纹理之间的关联,对线段进行分组获得了更多的筛选条件,增强了线段描述子对建筑物结构特性的描述能力, 从而提高线特征之间的区分度。
3 匹配模型
将线段组的描述元素的差异程度作为线段匹配的依据,对两组线段利用贝叶斯公式进行描述得到的匹配模型如下,在图像J中提取的线段组集合中寻找能够获得与图像I中提取的线段组集合中各线段组相似度各项得分最高的匹配线段LGj和LGi
LGjmax=argmaxLGjp(LGj|LGi)
(6)

(7)
其中,Z(LGj)为线段组LGj的正则化常数,φ(LGj,LGi)为线段描述子中与角度相关的项,表示两组线段的夹角度数和夹角中线度数分别差值的模型,c1表示φ(LGj,LGi)项的影响因数。ψ(LGj,LGi)为线段组中两线段元素最近点到各自端点的比例系数相关项,表示比例系数的差值模型,c2表示ψ(LGj,LGi)项的影响因数。其中,c1,c2∈(0,1),筛选项对匹配模型的影响比重小于纹理模型的占比。
两幅图像的线段组进行匹配时,首先比较①和②、③和④两侧的纹理标记Toutside,通过外侧邻域纹理标记粗筛之后得到相同标记的线段组候选集合。在候选集内进行夹角内侧纹理相似度的比较,两幅图像各自的线段组纹理的描述是基于灰度直方统计图,本文中选择巴氏距离作为纹理描述子相似度的比较模型,依照巴氏距离模型计算两组线段对应顺序的分区邻域纹理统计直方图概率密度分布情况的重叠率。对于两组线段的夹角内侧平面纹理Tinside_i和Tinside_j分别在同一区块part下统计得出的直方图离散概率分布情况hi和hj的像素灰度值分布区段X=[0,255],巴氏距离DB的定义可表示为
(8)
DB(hGi,hGj)=-ln(BC(hi,hj))
(9)
其中,BC(p,q)为Bhattacharyya系数
(10)
此时,hi(x)与hj(x)分别为两个直线的邻域内各区块统计直方图在灰度为x时的概率密度。
在匹配过程中,可以根据需要调整part的分区方法,目前有两种不同的分区方法,对匹配的效果各有侧重:方法一,将线段的邻域依照线段提取到的像素长度均分为part1个区块,所有的线段匹配时就可以一一对应地比较纹理相似度。方法二,固定分区的Member长度再依次逐个切分出part2个分区,进行线段匹配比较时,将短线段按照扫描的方式逐次与长线段对比分区纹理相似度,取匹配区块按升序排序后个数超过两者区块个数小者的百分比阈值的线段作为匹配线段,则它们的巴氏距离为逐次比较的巴氏距离最小值。第一种方法在匹配速度上比较有优势,计算量o(part1)小于o(part22)。第二种方法在出现遮挡情况时能更准确找到匹配的线段,如果相机移动过程中有较多遮挡物,应选方法二的分区模式。
在计算夹角内侧线段邻域纹理相似性比较后,所得到的候选匹配线段还需要满足建筑物的结构属性相似,即候选线段组的夹角大小差值小于阈值θi-θj<τθ,线段组夹角中线角度相近θmid_i-θmid_j<τθ_mid,线段组最近点到两条线段端点的距离比例差足够小λa_i/λb_i-λa_j/λb_j<τλ。对判断条件转化为贝叶斯公式评价表达,所以式(7)中的后两项表示的是结构属性的判断条件
φ(LGj,LGi)=φθinside(LGj,LGi)+φθmid(LGj,LGi)
(11)
(12)
(13)
(14)
满足以上条件的线段组匹配分数越高,因为结构属性有可容许限度,结构属性在线段组匹配中是必要而非充分条件,纹理统计直方图才是充分必要条件,利用参数c1和c2的取值调整属性对筛选匹配度的占比,使得纹理匹配作为主导评价。
4 线特征匹配应用
匹配线段可以应用在目标识别、三维重建中,对应线段对象能够匹配是计算的前提。建筑物结构上有丰富的线段特征,线特征可以表示建筑物的框架结构,也可以对面特征进行描述,这样的描述方法比点云模型更接近建筑物设计描述。相比于点云三维重建,利用线特征来描述建筑物的三维结构可以很好压缩数据量。利用线段匹配有利于克服遮挡问题,基于线段邻域纹理的匹配方法除去了线段长度这一比较维度,采用纹理的统计信息,容错性有很大的提升。
只需要3张建筑物的视图的对应线段就可以构建起3个视角的几何关系,利用三视图对应的匹配线段组可以解算出3个相机姿态矩阵的相对参数,将3幅图的匹配线段用各自的相机姿态矩阵映射形成三维空间中的平面,则理想状态下这3个平面的相交线就是线段在三维空间中的位置。存在误差的情况下,3个空间平面不相交于同一条直线,通过优化求解最小误差三维重建直线。
5 实验结果
本文提出的算法与文献[9]中的ICP算法进行对比。ICP算法是将最近点迭代求解整体误差最小值的一种点集匹配方法,为满足二维点集运算,在二维空间中将线段从欧式空间的线l=(a,b,c)降维到Hough空间由斜率和截距表示的点l=(θ,ρ),再对两幅图像的Hough空间上的点集利用ICP算法求解最近点,从而恢复对应的匹配线段。
用于实验测试的图像数据集以采集到的建筑物和线段匹配中常遇到的场景为例,实验图例如图4所示。图像为白天同一时段采集的两张图作为一组,模拟实时采集和处理图像的情况,相近时间采集的图像建筑物表面纹理受到的光照情况是相似的,对纹理灰度值的影响在算法可容许的范围内。通过机械小车搭载的相机,通过图像传感器和数据传感器反馈信息,由计算机端平台控制小车的移动和图像采集,模拟现实场景中的图像采集变化情况,所采集图像场景中部分是有绿化植物出现的并且被采集到图片素材库中。通过小车和相机相对建筑物的移动变化情况,将采集到的图像分为3种室外采集图像常见的情况:①旋转;②缩放;③透视变换。

图4 匹配实验测试样
对本次实验中基于邻域纹理的线特征匹配,在MATLAB平台上进行实验,采用的邻域宽度值为W=20,邻域像素影响因子的高斯系数σ=10,邻域分区数为part=5,线段分组最近点距离阈值τd=20,夹角误差阈值θ=15°。ICP算法也是在MATLAB平台上复现并进行运算。对相同的测试图片进行匹配实验,线段匹配结果见表1。
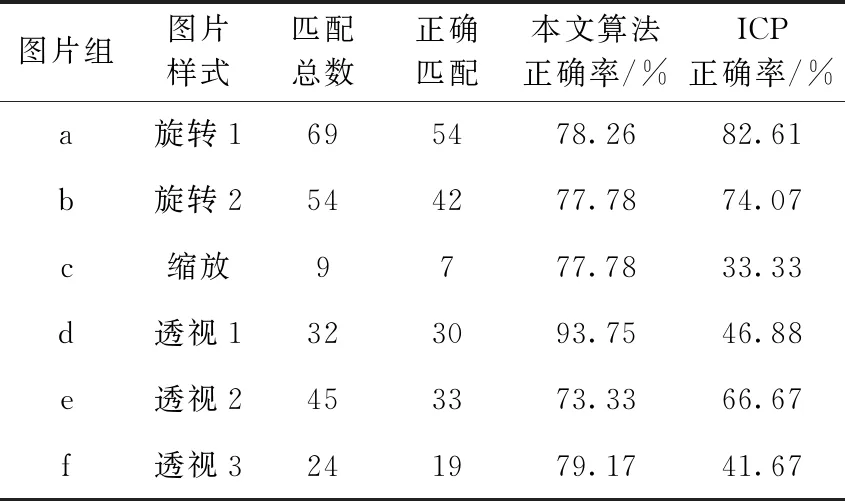
表1 线段匹配结果
本文中基于邻域纹理的线段匹配算法在旋转情况下的表现与ICP算法相当,而在缩放变换下,由于加入了图像金字塔的关系,本文算法的表现优于ICP算法。在透视变换中,各线段的旋转角度变化是与相机相对位移有关,所以图中的线段旋转变化程度是不相同的,这就使得ICP算法这个依靠投射到Hough空间后整体匹配的方法误差上升,而本文中依赖邻域纹理的方法就可以克服这一问题。
利用本文线段匹配方法,对目标建筑物分别在3个视角拍摄的图片进行线段匹配,如实验建筑物3个视角如图5所示。将3个视图中的直线进行匹配,最后得到相互匹配的线段组,共34组。利用这些匹配的线段数据计算三焦点张量和相机姿态矩阵,其中两组对应线段可构造一个求解方程组,则共有17组齐次方程可求解相机姿态矩阵,由于存在测量误差,利用最小二乘法求解关于17组齐次方程的相机姿态矩阵,得到的建筑物三维重建如图6所示。

图5 实验建筑物3个视角的拍摄图片

图6 建筑物线特征三维重建结果
在本文算法进行三维重建的结果中,可以看到右上角仍有5条树枝线段未被滤除并且进入三维重建的计算,这是由于树木这类自然界物体也拥有较长的线段架构,在线段提取时获得的线段元素超过了粗筛的阈值。而草丛和叶片较多的灌木已经被过滤,它们的短线段对象没有进入匹配计算和三维重建的过程中,提升计算的效率。
利用点特征三维重建算法作为对照组,对上述建筑物图像采用Colmap[10]重建方法,分别在相同的三视图情况输入和更多个视图的输入情况进行点云三维重建,多视图输入情况选取了同一建筑物的200张不同视角采集的图片。Colmap算法重建得到的稀疏点云分别如图7(a)和图7(b)中所示。

图7 Colmap算法点云三维重建
Colmap算法重建的结果对场景中的所有对象都进行特征得提取,在对象图片素材数量足够多时,可以对全场景中所有对象进行三维重建,200张输入图像可以获得73 513个特征点组成的点云,使得肉眼可以辩别出建筑物对象,但对于目标建筑物而言,树木、草丛的数据量增加会影响匹配和重建优化过程的效率。在图像素材只有3张时,Colmap算法的点云重建获得143个点特征的结果无法达到视觉上可辩别对象的程度。
由以上实验结果可以看出,利用线特征进行建筑物三维重建可以由线段之间的拓扑关系求解出完整的相机姿态信息,并恢复出建筑物大致的框架结构。相比于点云三维重建,在人造场景中线特征具有数据量小、对建筑物结构特征描述更清晰、可以达到所需要采集的数据量更少而达到相同的三维重建表达效果的优势。
6 结束语
本文针对建筑物识别与测绘标定过程中线段匹配问题,提出了基于线段邻域纹理统计的匹配方法,结合线段在建筑物框架上的位置特征,能够解决线段长度、方向变化对于匹配的影响,克服拍摄视点变化情况中的结构描述进行匹配迭代求解的固有误差对求解过程迭代收敛的影响。在缩放和视点变换状况下有效提升匹配的准确率,在一定程度上解决了线段在对称建筑结构上的区分问题。利用本文算法得到的匹配线段应用与三维重建,可以在图片数量相同的条件下重建出更完整的建筑物框架信息。

