云南某水电站地下厂房区地应力场模拟分析

刘 英，于立宏，孙凯辉，于 标

(1.吉林建筑大学，吉林 长春 130118；2.中国电建集团北京勘测设计研究院有限公司，北京 100024)

某水电站位于云南省怒江州六库镇，为高山峡谷深切割地貌形态，地下厂房尺寸(长×宽×高)：239.4m×30.1m×75.4m，位于怒江左岸，隔界河上游，上覆岩体厚200m，怒江侧、隔界河侧岩体水平厚度均大于1500m，岩性主要为片麻岩，岩石单轴饱和抗压强度80～90MPa，该区发育有断层f4、f8和f9，节理裂隙主要发育以下三组：①NE60～85°NW∠70～85°②NW310～330°NE∠70～85°③NW275～295°SW∠80～90°，其中以①组最为发育。该区地应力主要是由自重应力与构造应力共同作用的结果[1]，针对地下厂房区的勘察钻孔和勘探平洞内见有饼状岩芯和剥离现象，说明该区域地应力值发育较大[2]，地应力作用对地下厂房围岩稳定性将可能产生影响，该工程区地应力场发育情况，对于该水电站地下厂房设计意义重大[3]。

1 地下厂房区地应力场模拟分析方法

采用三维地应力场回归分析方法[4- 7]对该区地应场计算模拟，该方法基于研究区域的地形、地貌及钻孔、勘探平洞、测绘、试验等资料，分别建立单独施加重力荷载、x及y方向的两个法向均布荷载、切向均布荷载等4种工况下的三维有限元地质模型，建立计算方程组，式(1)分别计算出影响地应力场的各构造应力与自重应力单独作用下的有限元模型的“观测值”，与地应力“实测数据”按式(1)进行回归计算，采用多元线性叠加原理、最小二乘法拟合、偏差估计校验，确定回归系数。

σx=l1σxw+l2σxs1+l3σxs2+l4σxs3+ekσy=l1σyw+l2σys1+l3σys2+l4σys3+ekσz=l1σzw+l2σzs1+l3σzs2+l4σzs3+ekτxy=l1τxyw+l2τxys1+l3τxys2+l4τxys3+ekτyz=l1τyzw+l2τyzs1+l3τyzs2+l4τyzs3+ekτzx=l1τzxw+l2τzxs1+l3τzxs2+l4τzxs3+ek

(1)

式中，σx、σy、σz、τxy、τyz、τzx—钻孔处实测地应力值的6个应力分量；ek—随机变量；l1、l2、l3、l4—待确定的回归系数。

自重应力场σw、x方向水平构造应力场σs1、y方向水平构造应力场σs2、沿轴面逆时针方向水平切向应力场σs3独立作用下通过有限元计算所得到的6个应力分量。

2 模型构建

2.1 区域选取

模型计算区域根据地形地貌特征、厂房的位置、洞室的大小、埋深等因素[8]，选取隔界河、怒江河谷为模型边界，其余两个侧面边界及底边界考虑洞室开挖时应力影响范围(3倍洞径)及厂房空间大小，选取大于3倍洞径范围边界[9]，建立地下厂房所在区域的三维地质模型，点(0，1605，839)为相对坐标原点，S52°E方向为x轴正方向，N38°E方向为y轴正方向，z轴以垂直向上为正方向，x轴方向取785m长，y轴方向取460m宽，垂直方向取山峰顶至地下厂房以下共406m的高度值为模型计算区域。

2.2 参数选取

计算参数见表1—2。

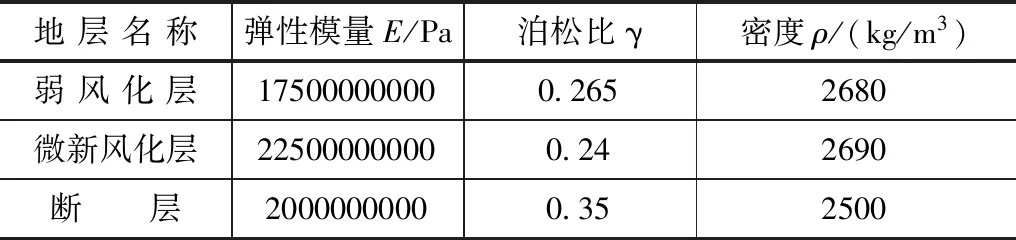
表1 岩体物理力学指标

2.3 三维有限元模型建立

把利用SolidWorks2010软件建立的三维几何模型[10]导入ABAQUS中，进行曲面几何修补[11]、地层区域划分、网格划分、自由网格技术划分计算单元，力学参数赋值及三维有限元计算、分析[12]。共划分19883个单元，29439个节点。三维有限元计算模型如图1所示。

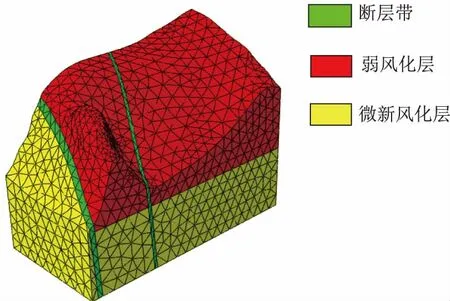
图1 地下厂房区有限元计算模型

2.4 模型加载

自重应力作用、x及y方向水平构造应力作用及切向分布构造应力作用下4种工况的三维有限元计算模型，四种工况的模型边界均采用约束x、y、z三个方向的平动自由度[13- 14]。

自重应力荷载模型，如图2所示，仅施加重力荷载，模型顶部自由，其他各边界采用位移约束。

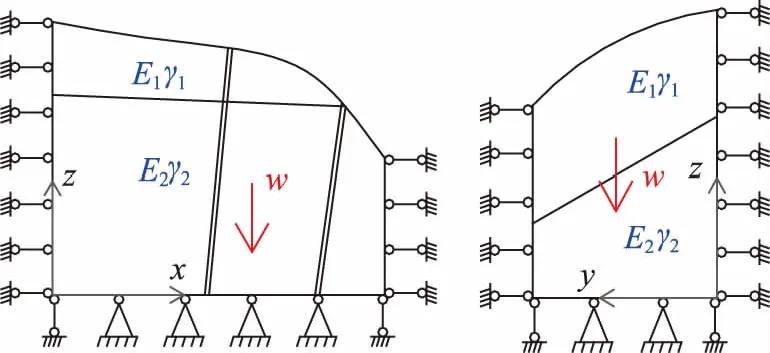
图2 自重应力荷载模型

沿y方向的法向分布构造应力荷载模型： 模型顶部自由，底部x方向自由，其他方向位移约束(除施加荷载边界外)，对模型一侧施加水平应力σs1，其量值取均布荷载1MPa，如图3所示。

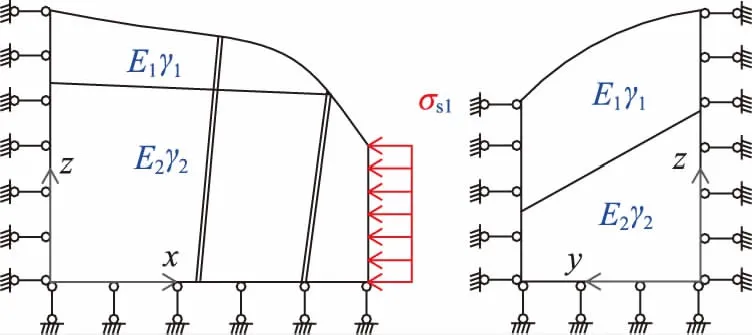
图3 Y方向的法向分布构造应力荷载模型

沿x方向的法向分布构造应力荷载模型：模型顶部自由，底部y方向自由，其他方向位移约束(除施加荷载边界外)，对模型一侧施加水平应力σs2，其量值取均布荷载1MPa，如图4所示。

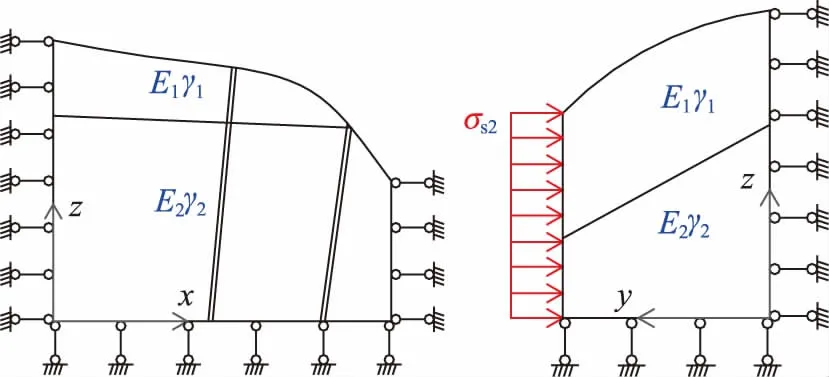
图4 沿X方向的法向分布构造应力荷载模型

切向分布构造应力加载模型：模型顶部自由，模型底部所有节点进行约束，对侧面边界法向约束，其他自由。对切向应力σs3施加单位均布荷载1MPa，方向沿x轴方向逆时针加载，如图5所示。

图5 切向分布构造应力加载模型

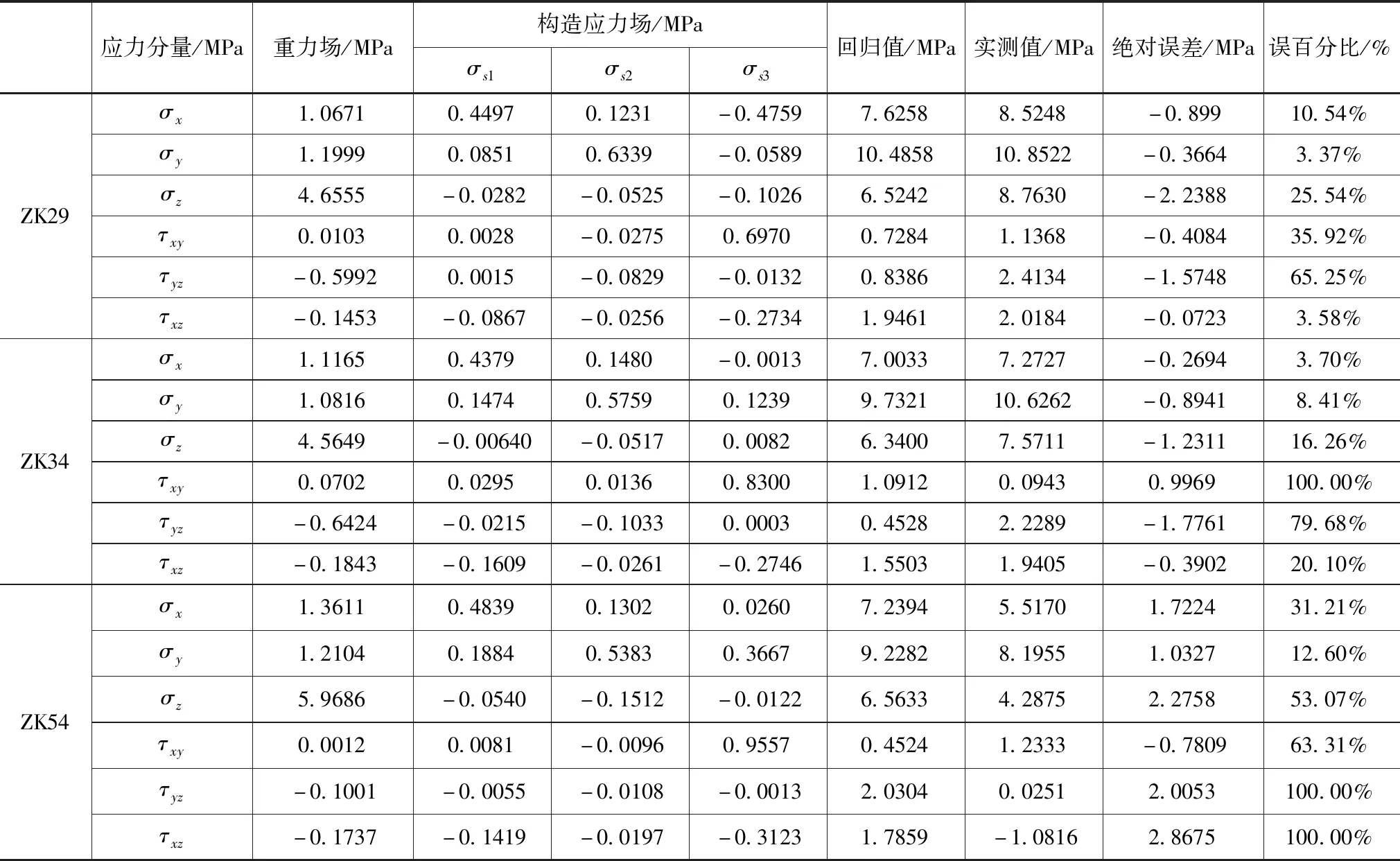
表3 ZK29、ZK34、ZK54地应力实测值与回归值对比表

3 地应力场反演分析

3.1 地应力场回归方程

根据探入地下厂房岩体内的钻孔ZK29、ZK34、ZK54三维地应力实测数据，见表3，将大地坐标系向SE方向旋转52°，即将大地坐标系变为模型坐标系[15]，得到模型坐标系下的三维地应力应力分量的测量值，见表4。

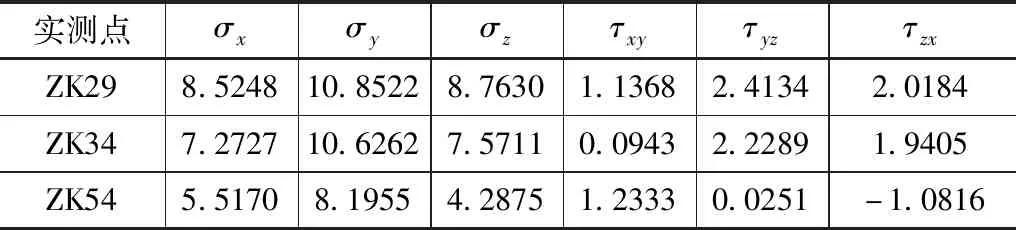
表4 模型坐标系下的三维地应力测量值 单位：MPa

通过模型坐标系下的三维地应力应力分量的测量值与4个三维有限元地应力模型模拟结果，利用MATLAB软件对表4内数据采用多元线性回归进行拟合计算[16]，求得式(1)系数数值，分别为：

l1=1.0184，l2=4.7585，l3=10.2294，l4=-1.8368，ek=-2.2660

复相关系数校验，R=0.9258，对比各测点(ZK29、ZK34、ZK54)处地应力实测值与回归值结果，见表3，模型中6处剪应力回归值与实测值的误百分比高于60%，由于剪应力在量值上普遍较小，因此主应力的回归结果不会受过多的影响。而其余各观测点的应力回归值与实测值拟合较好，与各测点的实测值较为接近。综上所述，该地下厂房区地应力场回归拟合较好，符合实际情况[17]。

即地应力场回归方程为：

σ=10184σw+47585σs1+102294σs2- 10184σs3-2266

(2)

式中，σ—地应力场回归值。

3.2 地应力场模拟分析

利用式(2)地应力场回归方程，输出的各节点的应力值与坐标值，建立应力分量拟合函数方程：

σx=3000x+2000y+18000z-16594000σy=4000x-6000y+2800z-4538600σz=3000x-3000y+23000z-32503000τxy=0.0219σ1+0.0968σ2+0.0277σ3τyz=0.208σ1+0.111σ2-0.1845σ3τzx=0.1161σ1-0.0037σ2+0.0768σ3

(3)

模型顶部约束自由，约束模型其他5个边界，如图2所示，以体力形式将模型施加自重应力，利用FORTRAN语言编写初始地应力场式(3)函数程序，利用ABAQUS用户子程序SIGINI来实现初始地应力场模拟。

经数值模拟计算，获得地下厂房区地应力场主应力云图(如图6所示)及主应力矢量图(如图7所示)。

图6 最大主应力、中间主应力、最小主应力云图

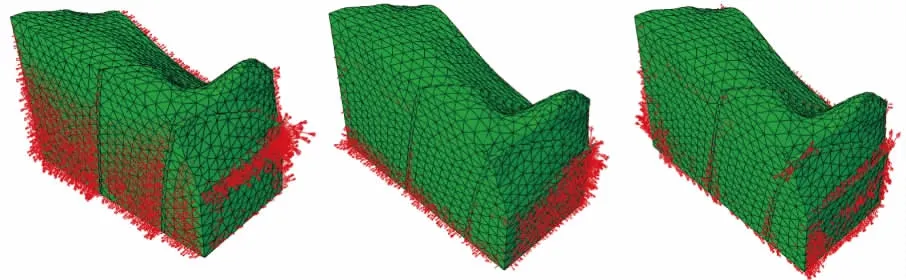
图7 最大主应力、中间主应力、最小主应力矢量图

图6—7可以看出地下厂房区任一点地应力发育情况，地下厂房区地应力场以水平构造应力为主，最大主应力量值范围为12～15 MPa，应力方向为NE～NEE，向SWW倾伏，倾角约为30°，中间主应力量值范围为7～9 MPa，向 NWW倾伏，最小主应力量值范围约为5～7MPa，向SEE倾伏。综上分析，地下厂房区为中等地应力区，又因为，地下厂房区岩石单轴饱和抗压强度80～90MPa，所以，地下厂房在开挖过程中有发生轻微岩爆的可能，发生其它级别岩爆的可能性不大。

4 结语

本文利用实测地应力数据，运用ABAQUS与MATLAB软件进行数值仿真模拟、多元线性回归分析，反演出地下厂房区地应力场发育特征、分布规律，据此，分析判断出地下厂房在开挖过程中有发生轻微岩爆的可能，为地下厂房围岩支护设计提供了前瞻性指导。

由于实测地应力数据较少，本文分析得出的地应力场精度略显不足，期待下一阶段再对该地下厂房区进行三维地应力实测，对此地应力场进行验证的同时，增加实测数据，提高反演精度。工程建设前应对工程建设过程中可能遇到的问题进行深入分析研判，并提出工程处理方案，这样才是最优工程设计的前提。