数学课堂中的“言之、辨之、明之”
江苏省苏州工业园区星洋学校 杨雪华
综合一线教学的实践和实验,笔者得出的结论是:学生在课堂上的疑惑是教师教学最宝贵的资源。教学中,有时学生的想法和我们的教学意图“截然相反”,甚至是“不可思议”的。然而,学生和教师的视角也经常是不一样的,他们的想法表面上看还是言之有理的。下面,笔者通过几个课堂教学实例和各位同行一起探讨交流。
一、课堂教学应透析数学概念本质
数学概念的建构是由具体到抽象的归纳提炼过程,我们对概念的认知是从感性向理性逐步过渡形成的,所以,剖析概念中的关键要点、重构概念、透析其生成过程尤为重要。教师在教学过程中要重视概念辨析,充分利用对比教学、类比分析等方法,抓住概念本质,同时,对课堂上的疑惑,要鼓励学生敢于直面不解或误解,让其成为我们的教学资源库,指导我们的教学,提高课堂教学效率。
1.言之、辩之、明之:“过两点我画出了两条直线?”
笔者曾执教过一节市级公开课,一位学生在课堂上提出:“‘经过两点有一条直线,并且只有一条直线’这句话是错的。”他用操作来证明自己的观点——“经过两点,我画出了两条直线”。笔者:“你的观点很好,看你画的图形,好像过两点还可以再画一条。”“对,还可以画一条。”笔者顺水推舟:“按这样的画法,一共可以画几条呢?”班上学生开始讨论,随即画出的条数越来越多,有学生总结:“点越大,画出的直线条数就越多。”有同学反驳:“老师,点是没有大小的。”抓住时机,笔者立即给予表扬:“总结得很好,那为什么过两点可以画很多条直线呢?”辩论正式开始……
善于仔细观察和思考,关键时刻能够说出自己的想法,动员学生一起辩论,数学原理蕴含的道理自然而然就会明晰,问题也能得到解决。
2.言之、辩之、明之:“方程x+y=y+2 是一元一次方程,还是二元一次方程?”
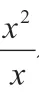
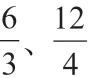
二、课堂教学应避免解题经验的负迁移
迁移是已经获得的知识技能和学习方法对新知识和新技能获取的影响,它分为正迁移和负迁移,如果一种知识技能的掌握能够促进另外一种知识技能的掌握,那就是正迁移,反之就是负迁移。在一线教学实践中,我们时常会遇到负迁移的发生,一般我们把这种现象归为学生“审题不清、读题不准”,但是透过现象看本质,这其实是负迁移的影响,这需要我们在教学中创设精准的前学情境,运用好正向迁移的规律,促使学生有效学习。一线教师在总结解题规律时要谨慎,积累数学经验要注意条件和前提,避免出现“负迁移”现象。
言之、辩之、明之:“平面直角坐标系中,直线从左向右呈上升趋势,表示对应速度不断加快。”
试题呈现:星期天上午,小明从家里出发,以速度m1走到书店买书,在书店待了一段时间,然后以速度m2继续向前,走到书店前方的一个广场休息(m1>m2),下列能正确反映出发时间t(小时)与他行走的路程S(千米)之间的函数关系图像是( )。
有学生说了他的解题思路:“小明行走的两段路,速度是先快后慢,所以选C。”有学生表示反对:“题目中‘在书店待了一段时间’,表明此时路程不变,时间在改变。所以A、C 肯定是错的,选B。”对此,有学生表示支持:“对,应该选B,线段从左向右走势越陡,表明速度越快。”最后一位学生说出自己的想法:“老师,我怀疑B和D 的图像,我觉得应该选D,因为函数图像表示的是时间t 与路程S 的函数关系,它并不是我们常见的路程与时间的函数关系。”
数学课堂上,笔者觉得只有“放手”,让学生大胆“言之”,学生的思维才能被激活,进而出现教师所期盼的“辨之”,我们才有机会和学生一起讨论和“理之”,最后师生达成共识,才能将概念生成、数学原理、解题思路等科学有效地“明之”。数学课堂上,学生的“言之有据”“顺理明理”是数学教师最好的教学素材,让学生勇敢地不耻下问、积极参与辩论、有效交流探究,最终师生达成共识:明白学习、清晰理解。这就是数学课堂真正意义上的“言之、辩之、明之”。

