考虑聚合物非牛顿性和渗流附加阻力的 海上油田早期注聚效果评价方法

刘 凡，吴学林，周文胜，王 凯

（1.中海油研究总院有限责任公司，北京 100038；2.海洋石油高效开发国家重点实验室，

北京 100038；3.中国石油勘探开发研究院，北京 100083）

目前判断聚合物注入有效性的主要方法是根据现场数据绘制霍尔曲线，通过聚合物驱（聚驱）阶段与水驱阶段斜率的变化来判断注聚是否有效[1-2]，并根据斜率计算阻力系数和残余阻力系数[3]。但是海 上油田早期聚驱不同于陆上油田中后期聚驱，其主要特点是注聚时间早，水驱阶段短，甚至投产即注聚，不存在水驱阶段[4]，因此传统霍尔曲线不适用于海上油田早期聚驱评价。另外，海上油田早期聚驱开发，地下流体的主要组成为油和聚合物溶液。由于海上油田用的疏水缔合型聚合物属于非牛顿流体[5]，而常规霍尔曲线是在牛顿流体的基础上建立起来的[6]，因此，海上早期聚驱对霍尔曲线法评价的可靠性及可适用性都提出了新的要求。刘睿[7]在考虑地下流体非牛顿性的基础上建立了改进的霍尔曲线，可以得到地下聚合物溶液的流态指数、波及范围内的平均有效工作黏度、阻力系数等指标，用来评价海上油田早期聚驱开发效果。张志英等开展的聚驱实验结果表明[8]，聚合物驱油时存在附加阻力效应，对聚驱开发动态预测产生较大影响。因此，需要对霍尔曲线进一步完善。

本文在分别考虑聚合物溶液的非牛顿性和附加阻力效应的基础上，建立了适合评价海上油田早期聚驱效果的改进霍尔曲线。根据改进霍尔曲线的斜率和截距，可以求解出注聚任意时刻地下聚合物溶液的流态指数、波及范围内的平均有效工作黏度、流度、阻力系数、启动压力梯度等指标，对早期注聚有效性进行更准确地评价。

1 数学模型

1.1 假设条件

为满足海上油田开发评价的需要，结合海上早期聚驱开发的特点，在借鉴常规霍尔曲线构造的基础上推导出改进霍尔曲线公式，提出了以下几条改进霍尔曲线构造的基本假设条件:①地层均质、等厚、各向同性；②流体呈平面径向流动，忽略毛管力、重力，以及岩石和流体的压缩性和温度的影响；③注入流体为非牛顿假塑性流体，性质与其在地层中流体性质相同，其本构方程[9]遵循Ostwald-de Waele 幂律模式；④流体在岩石多孔介质中的等效剪切速率计算公式如式（1）[10]；⑤流体为油水两相，聚合物只存在于水相中；⑥考虑注入聚合物的非牛顿性；⑦考虑注入聚合物的附加阻力效应；⑧注入方式为早期注聚，即投产即注聚。

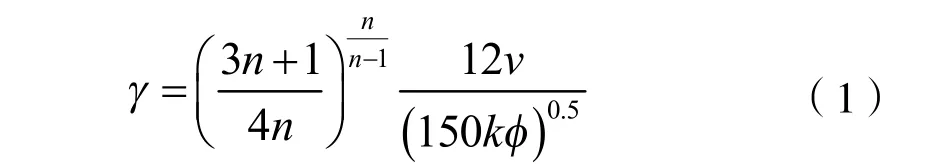
式中:γ 为等效剪切速率，s-1；v 为毛管中的平均流速，m/s；k 为地层渗透率，μm2；φ 为地层孔隙度，%；n为流态指数（0 1n＜ ＜ ）。

1.2 考虑启动压力梯度的改进霍尔曲线公式

在分别考虑聚合物溶液的非牛顿性[11]、启动压力梯度的基础上，构建出了适合海上油田早期注聚效果评价的改进霍尔曲线公式。

考虑附加阻力影响，假设条件为投产即注聚，注入井井底压力为:

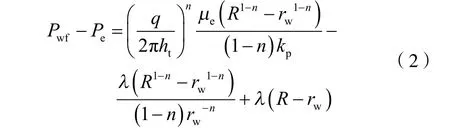
式中:wfP 为注入井井底压力，MPa；eP 为地层压力，MPa；q 为总流量，m3/d；eμ 为地下聚合物溶液的平均工作有效黏度，mPa·s；λ 为启动压力梯度，MPa/m；R为聚合物驱替的前缘位置，m；th 为油藏总有效厚度，m；wr 为井筒半径，m；pk 为聚合物溶液在地层中流动时的渗透率，μm2。

考虑注聚后，聚合物溶液的吸附滞留可能引起地层渗透率下降，则用渗透率下降系数对式（2）中的pk 进行校正:

式中:kR 为渗透率下降系数，无因次。

将式（3）代入式（2），化简后得任意小层的注入井井底压力:

实际开发中常常有短暂的水驱阶段，可以用式（7）计算:

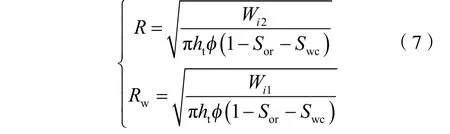
式中: Wi1为早期注聚前期水驱的累计注入量，m3；Wi2为水驱后聚合物溶液的累计注入量，m3； Sor为残余油饱和度，无因次； Swc为束缚水饱和度，无因次。

式中:T 为累计注入时间，d。

式（13）即为同时考虑了注入聚合物溶液的非牛顿性、启动压力梯度及多层油藏的非均质性的改进霍尔曲线b 的表达式。

2 评价指标

利用改进的霍尔曲线a 和霍尔曲线b，建立早期聚驱效果的评价指标。

2.1 流态指数

由式（12）可以看出:改进霍尔曲线a 中聚驱段的斜率，在数值上等于地下聚合物溶液波及范围内的平均流态指数（n）。

2.2 平均工作有效黏度

由式（13）和式（12）可以看出，eμ 是改进的霍尔曲线b 斜率C 中的未知项，因此，根据该斜率可以求出eμ 为:

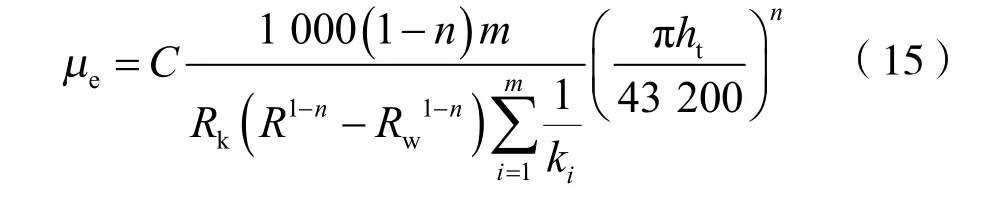
上式求出的eμ 即为聚合物溶液在地下的平均工作有效黏度，是随着注聚时间的长短而变化的量。

2.3 工作流度

根据流度的定义可得地下聚合物溶液的工作流度为:

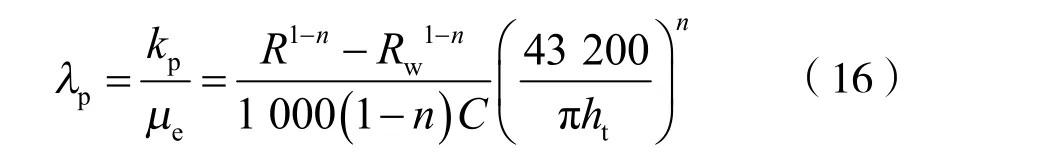
式中:pλ 为地下聚合物溶液的工作流度，μm2/（mPa·s）。

因此，已知改进霍尔曲线的斜率及截距后，即可求出地下聚合物溶液的工作流度。

2.4 流动系数

根据流动系数的定义可得地下聚合物溶液工作时的流动系数为:

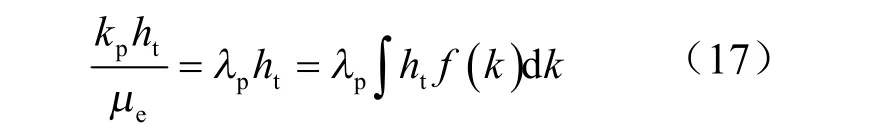
因此，通过式（16）得到地下聚合物溶液的工作流度后，便可由式（17）求出地下聚合物溶液工作时的流动系数。

2.5 早期注聚的阻力系数

阻力系数，又称阻力因子，指聚合物驱过程中水的流度与聚合物溶液的流度之比。阻力系数是衡量聚驱时流度比改善的一个标准，若其值明显增加，则表明聚合物溶液改善油水流度比的能力增强。

由阻力系数定义得:

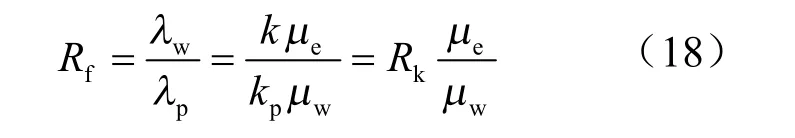
式中:Rf为阻力系数，无因次；μw为水在地下的平均工作有效黏度，mPa·s。

2.6 注入聚合物的启动压力梯度

由式（13）和式（14）可以看出，启动压力梯度λ 是改进霍尔曲线b 截距B中的未知项，因此，根据该斜率可以求出λ 为:

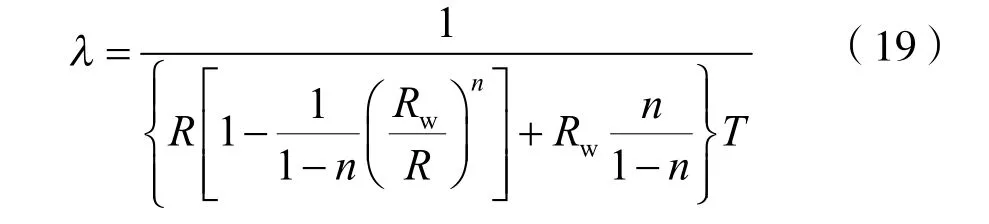
3 实例应用

由图1 可知，由于水驱时间太短，传统的霍尔曲线方法无法利用水驱段和聚驱段的斜率比得出阻力系数。应用改进霍尔曲线聚驱段的斜率和截距，可得到各参数的计算结果。由表1 看出，考虑附加阻力后计算结果比不考虑附加阻力计算结果大。这是因为考虑附加阻力时，聚合物流动需要一定的启动压力，因此霍尔曲线的斜率不变，截距增大。聚合物地下工作黏度与截距成正比，因此在考虑附加阻力后，地下聚合物流态指数不变，工作黏度比不考虑附加阻力时所得的结果大，流动系数较小。

3.1 实际注入井早期聚驱效果

渤海典型油藏A 井油层平均渗透率5 000×10-3μm2。注水31 d 后开始注聚，聚合物产品选用疏水缔合聚合物（AP-P4），注聚浓度为1 750 mg/L，井口注入黏度24.6 mPa·s，平均日注入量355 m3。根据A 井开发1 531 d 的动态数据绘制传统的霍尔曲线和改进的霍尔曲线（图1、图2）。

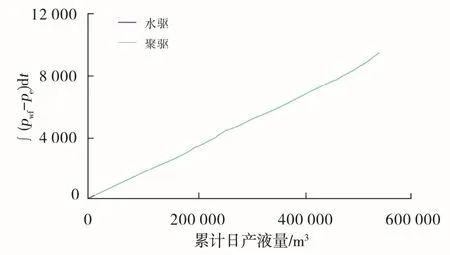
图1 渤海典型油藏A 井传统霍尔曲线

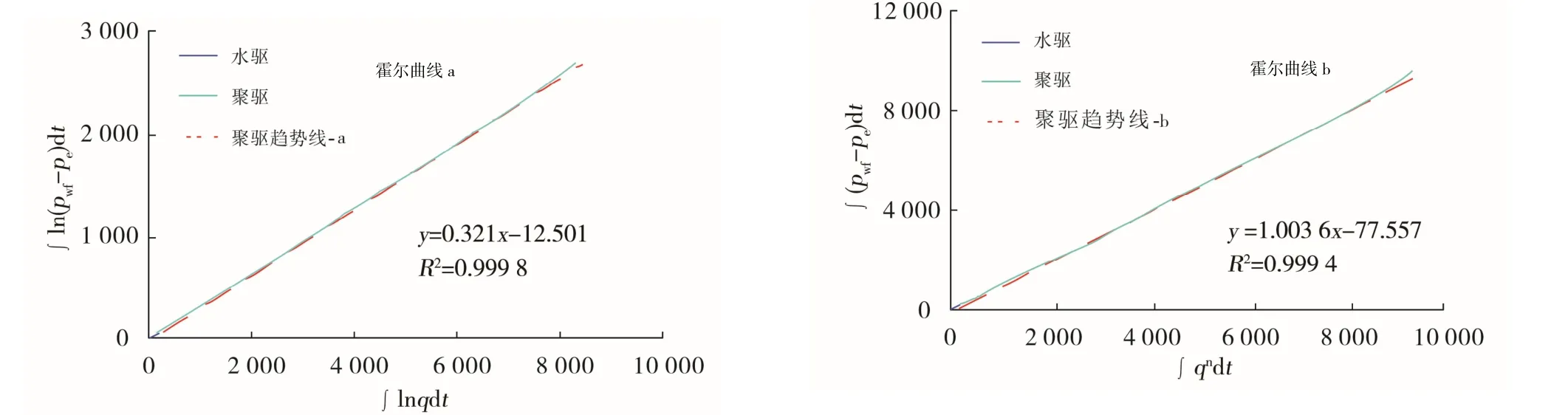
图2 渤海典型油藏A 井改进霍尔曲线

表1 渤海典型油藏A 井改进霍尔曲线的各项计算参数

3.2 实验验证

液体进入岩心后需要克服一定的阻力才能开始流动。当注入压力大于启动压力时流体将持续从出口端流出；当注入压力小于启动压力时，流体停止流动；当注入压力恰好等于启动压力时，流体将处于流动前的临界状态[12]。利用毛管平衡法对聚合物的启动压力梯度进行测量。

启动压力的测定方法如下:①将一定黏度聚合物注入岩心直至压力保持平稳且出口端出现聚合物溶液；②在岩心两端安装竖直长管，以便形成U 形管。其中，出口端接大气，进口端固定一只装有相同黏度聚合物溶液的容器并保持一定高度；③保持足够长时间以后，两边液面稳定于某个高度差，记录这个高度差，并根据式（20）换算成压差，这个压差就是启动压力，可进一步换算成启动压力梯度。

式中:P为压差，Pa；ρ 为液体密度，kg/m3；h为岩心两端液柱高度差，m。

选择三个渗透率水平（1 500×10-3，2 000×10-3，2 500×10-3µm2）的岩心进行毛管平衡法注入实验。由于现场实际注入的聚合物溶液会在井筒中流动并产生剪切降黏效应，当聚合物溶液到达井底时的黏度约为10～12 mPa·s。因此，实验中配制聚合物溶液黏度为10 mPa·s，得到不同渗透率岩心的启动压力梯度（图4）。

由图4 可知，渗透率越低，启动压力梯度越高。当聚合物注入黏度为10 mPa·s 时，启动压力梯度（λ）与渗透率（k）之间关系:λ=0.007 8e-0.4581k。将该式应用于渤海典型油藏A 井，得到A 井的启动压力梯度为0.003 MPa/m，与应用改进霍尔曲线得到的附加阻力数值相近。

3.3 地下聚合物溶液参数随时间的变化

对渤海典型油藏A 井，应用改进霍尔曲线计算地下聚合物溶液的流态指数、工作有效黏度、流动系数和阻力系数随注聚时间的变化（图5）。

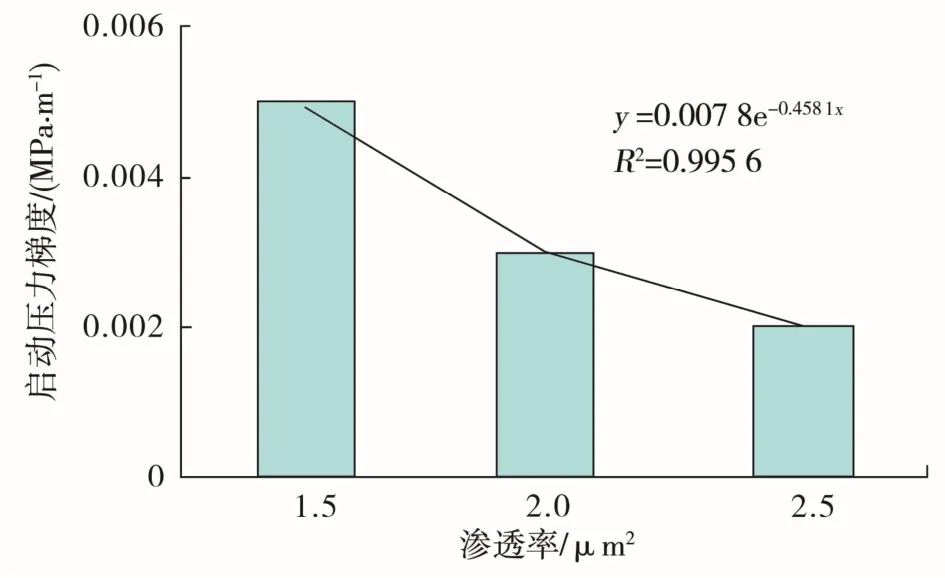
图4 毛管平衡法测定不同渗透率岩心的启动压力梯度

由图5 可以看出，随着注聚时间的延长，流态指数略有增加，但变化不大；流动系数增大，阻力系数减小，波及范围内的地下聚合物平均工作有效黏度减小。这是由于注入的是同一种聚合物溶液，聚合物波及范围内的非牛顿性略有减弱，但变化不大。注聚后聚合物溶液的工作有效黏度由于受到机械剪切、吸附等作用的影响，注聚4 a 后约损失50%，阻力系数减小，流动系数增加，改善油水流度比的效果逐渐变差。

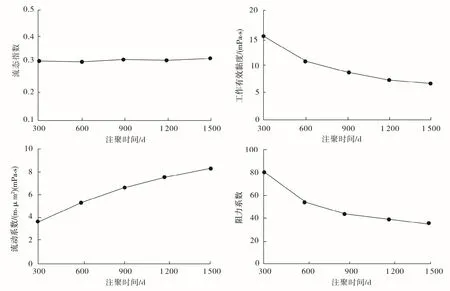
图5 地下聚合物溶液参数随注聚时间的变化

4 结论

（1）对于海上油田注聚时间早、水驱时间短的情况，常规霍尔曲线无法计算阻力系数。而改进的霍尔曲线在考虑附加阻力的基础上，直接利用生产动态的变化，得到波及范围内地下聚合物溶液的平均工作有效黏度这个重要指标，通过聚合物黏度与水黏度的比值得到阻力系数。解决了早期注聚阻力系数无法求解或求解无效的问题。

（2）改进霍尔曲线通过压差和流量的数学变化， 可以计算得出地下聚合物流动的附加阻力。将计算方法得到的附加阻力与实验结果进行验证，数值相近，说明该方法计算的附加阻力具有一定的可靠性。

（3）随着注聚时间的延长，地下聚合物溶液的非牛顿性略有减弱，但波及范围内地下聚合物平均工作有效黏度受到机械剪切、吸附等作用的影响，损失较大，致使地下聚合物溶液流动系数增大，阻力系数减小，改善油水流度比的效果逐渐变差。