基于机器学习的织物疵点检测
王 帅,岳鹏飞,董晗睿,侯 爽,余灵婕,*
(1.西安工程大学 纺织科学与工程学院,陕西 西安710048;2.西安工程大学 功能性纺织材料及制品教育部重点实验室,陕西 西安710048)
织物疵点检测是纺织行业一道很重要的质量控制工序,织物出厂前均要经过疵点检验、识别及鉴定,作为贸易结算的主要依据。传统方法的织物疵点检测是人工视觉检测来完成,该方法存在检测速度低,验布结果受验布人员主观影响较大,有误检率、漏检率高和人工成本大等缺点,所以纺织品的人工检验方法将逐步被基于机器视觉、图像处理和人工智能的自动检测技术所取代。Ding[1]采用的织物疵点检测算法提取织物的HOG 特征是基于方向梯度直方图(Histogram of Oriented Gradient,HOG)和支持向量机(Support Vecto Machine,SVM)的,进一步利用支持向量机对织物瑕疵进行分类检测。刘绥美等[2]基于形态学和稀疏表示模型对织物瑕疵区域进行定位检测。Liu等[3]对单色布匹疵点进行分类,他们结合了粒子群算法和反向传播算法(Back Propagation,BP)。本文选用一定数量的织物疵点图片作为疵点数据集,疵点种类包括破洞、稀纬、断经、结头、棉球、沾色、带纱等,利用决策树、随机森林、支持向量机3种算法对疵点数据进行模型建立,采用交叉验证的方法得出效果最佳模型。
1 相关工作
1.1 决策树
决策树(Decision Tree)是一种非参数的有监督学习方法,它能够从一系列有特征和标签的数据中总结出决策规则,并用树状图的结构来呈现这些规则,以解决分类和回归问题。决策树算法容易理解,适用各种数据,在解决各种问题时都有良好表现,尤其是以树模型为核心的各种集成算法,在各个行业都有广泛的应用。

图1 决策树模型
在决策树生成的随机过程中,每个结点分裂根据结点上训练数据的最优特征来划分。最优特征选择是在训练数据中选出分类效果最好的特征来划分特征空间,这样有助于提升决策树的效率,避免使用无分类能力的特征。最优特征选择有多种衡量指标,最常用的有信息增益、信息增益比和基尼指数等[4]。
为了说明信息增益、信息增益比的关系,先给出信息熵的定义。信息熵(information entropy)是度量样本集合纯度最常用的一种指标。假定当前样本集合D中第k类样本所占的比例为Pk(k=1,2…,|y|),则D的信息熵定义为:

Ent(D)的值越大,则D 的知度越高。
假定离散属性a 有V 个可能的取值{a',…a.,}若使用a 来对样本集D 进行划分,则会产生V 个分支结点,其中第0个分支结点包含了D 中所有在属性a上取值为a"的样本,记为D"。可根据式(1)计算出DV的信息熵,再考虑到不同的分支结点所包含的样本数不同,给分支结点赋予权重即样本数越多的分支结点的影响越大,于是可计算出用属性a 对样本集D 进行划分所获得的“信息增益”(information gain):
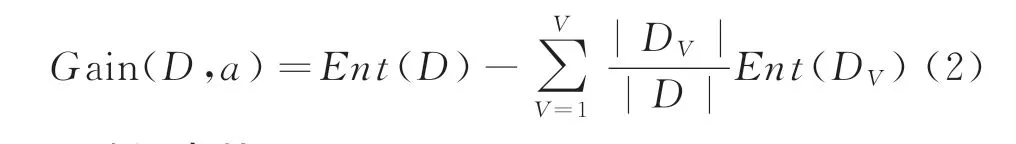
1.2 随机森林
随机森林(Random Forest,简称RF)是Bagging的一个扩展变体。随机森林在以决策树为基学习器构建Bagging集成的基础上,进一步在决策树的训练过程中引入了随机属性选择。具体来说,传统决策树在选择划分属性时是在当前结点的属性集合(假定有d个属性)中选择一个最优属性;而在随机森林中,对基决策树的每个结点,先从该结点的属性集合中随机选择一个包含k 个属性的子集,然后再从这个子集中选择一个最优属性用来划分[5]。
1.3 支持向量机
支持向量机的分类方法,是在一组分布中找出一个超平面作为决策边界,使模型在数据上的分类误差尽量小一点,尤其是在未知数据集上的分类误差(泛化误差)尽量小。线性SVM 可以看成是神经网络的单个神经元(虽然损失函数与神经网络不同),非线性的SVM 则与两层的神经网络相当,非线性的SVM 中如果添加多个核函数,则可以模仿多层的神经网络。
1.3.1 定义决策边界
取N 个训练样本,每个训练样本可以被表示为(xi,yi)(i=1,2,…N),其中(xi)是这样的一个特征向量,每个样本总共n个特征;二分类标签yi的取值是{-1,1}。如果n等于2,则有i=(x1i,x2i,yi)T分别由特征向量和标签组成。此时可以在二维平面上,以x2为横坐标,x1为纵坐标,y 为颜色,来可视化所有的样本(图2)。
紫色点的标签为1,红色点的标签为-1。在这个数据集上寻找一个决策边界,在二维平面上,决策边界(超平面)就是一条直线。紫色点所代表的标签y 是1,所以规定P >0,红色点表示的标签y 是-1。

图2 样本可视化(1)
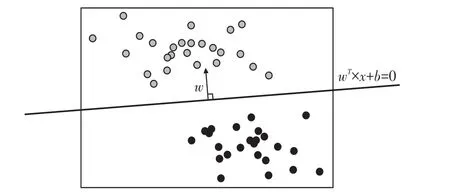
图3 样本可视化(2)
平行于决策边界的2条线的表达式:w×x+b=1,w×x+b=-1。 表达式两边的1和-1分别表示了2条平行于决策边界的虚线到决策边界的相对距离。此时,让这2条线分别过2类数据中距离决策边界最近的点,这些点就被称为“支持向量”[6]。如图3、图4所示。
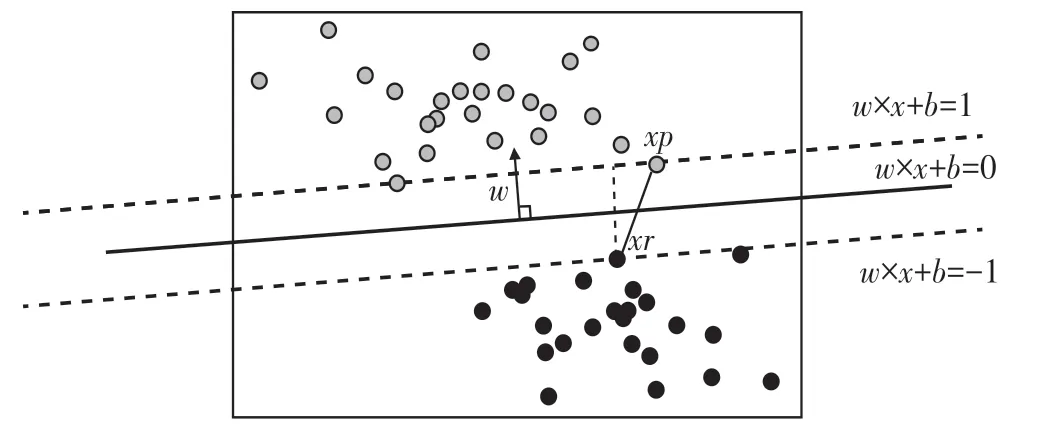
图4 样本可视化(3)
1.4 织物疵点检测的对象
随机抽取了破洞、稀纬、断经、结头、棉球、沾色、带纱等7类疵点类型[7],每种类型随机抽取了图片,共计有3 000幅疵点图片。为了与标准样对比,又选取了1 000幅无疵点图作为标准。为了运算方便,每张图片大小为200像素×200像素,如图5所示。每个数据集上试验10次,取平均值作为试验结果,以尽量避免试验的偶然性。试验中采用的计算机硬件配置为:GPU RTX 2080Ti,内存32 GB。
2 机器学习算法的模型设计
机器学习的分类方法如图6所示。
2.1 决策树模型
2.1.1 重要参数设计
(1)criterion选择
criterion 是用来决定不纯度的计算方法的,sklearn提供了2种选择:
输入“entropy”,使用信息熵(Entropy);
输入“gini”,使用基尼系数(Gini Impurity)。

图5 疵点分类图
比起基尼系数,信息熵对不纯度更加敏感,对不纯度的惩罚最强,但是在实际使用中,信息熵和基尼系数的效果基本相同。信息熵的计算比基尼系数缓慢一些,因此对于高维数据或者噪音很多的数据,信息熵很容易过拟合,选择基尼系数的效果往往比较好。试验测试得出criterion=‘entropy’。
(2)random_state&splitter选择
random_state用来设置分枝中的随机模式的参数,默认none,在高维度时随机性会表现更明显,低维度的数据,随机性几乎不会显现。这是防止过拟合的一种方式,试验测试得出random_state=800。
(3)剪枝参数max_depth
sklearn有不同的剪枝策略:max_depth限制树的最大深度,超过设定深度的树枝全部剪掉。决策树多生长一层,对样本量的需求会增加一倍,所以限制树深度能够有效地限制过拟合,在集成算法中也非常实用。实际使用时,从=3开始尝试,看看拟合的效果再决定是否增加设定深度,试验得出max_depth=6。
数据拟合情况如图7所示。

图7 数据拟合情况
2.2 随机森林模型
2.2.1 重要参数设计
(1)criterion选择
对于高维数据或者噪音很多的数据,信息熵很容易过拟合,选择基尼系数的效果往往比较好[8]。试验测试得出criterion=‘gini’。
(2)n_estimators选择
这是森林中数木的数量,即评估器的数量。n_estimators越大,模型的效果往往越好。任何模型都有决策边界,n_estimators达到一定的程度之后,随机森林的精确性往往不再上升或开始波动,并且n_estimators越大,需要的计算量和内存也越大,训练的时间也会越长。试验参数n_estimators=131,在训练难度和模型效果之间取得平衡,如图8所示。
(3)max_features选择
有增有减,默认auto,是特征总数的开平方,位于中间复杂度,既可以向复杂度升高的方向,也可以向复杂度降低的方向调参max_features↓,模型更简单,图像左移max_features↑,模型更复杂,图像右移max_features是唯一的,既能够让模型更简单,也能够让模型更复杂的参数,所以在调整这个参数的时候,选择auto。
(4)min_samples_split选择

图8 n_estimators效果图
有增有减,默认最小为2,即最高复杂度,向复杂度降低的方向调参min_samples_split↑,模型更简单,且向图像的左边移动。试验选取min_samples_split=10。
(5)random_state选择
试验测试得出random_state=800。
2.3 支持向量机模型
(1)数据可视化。对疵点数据前2列数据可视化,判断其为偏线性关系,如图9所示。

图9 数据可视化图
(2)数据标准化。使用数据预处理中的标准化的类,对数据进行标准化。标准化完毕后,再次让SVC 在核函数中遍历,观察疵点数据是否存在量纲问题,观察表10中数据最小值(min)和1%的数据存在偏差,存在量纲不统一问题,对疵点数据进行无量纲化[9]。

图10 标准化疵点数据图
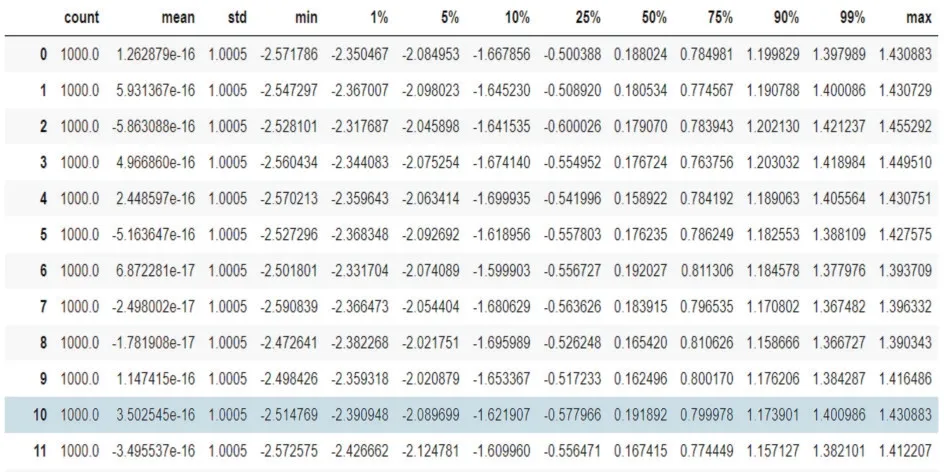
图11 无量纲化数据图
经过无量纲化后,模型准确率下降,因此不对疵点数据集进行无量纲化处理[10],如图11所示。
(3)核函数选择。核函数参数见表1。
根据模型效果,核函数选择"rbf",如图12 所示。使用循环函数对"rbf"参数gamma选择最优值,得出模型准确率0.72,gamma取值1.39e-07。

表1 核函数参数图
(4)random_state选择
试验测试选择random_state=800。
3 试验方法与结果
3.1 方法
采用交叉验证方法交叉验证[11](cross_val_score)是用来观察模型的稳定性的一种方法,将数据划分为n份,依次使用其中一份作为测试集,其他n-1份作为训练集,多次计算模型的精确性来评估模型的平均准确程度。训练集和测试集的划分会干扰模型的结果,因此用交叉验证n 次 的结果求出平均值,是对模型效果一个更好的度量。
使用交叉验证用于评估模型的预测性能,尤其是训练好的模型在新数据上的表现[12],能够在一定程度上减小过拟合。数据量大的时候,k 可以设置的小一些,数据量小的时候,k 可以设置的大一些。在试验中交叉验证次数选取15次。如图13所示。
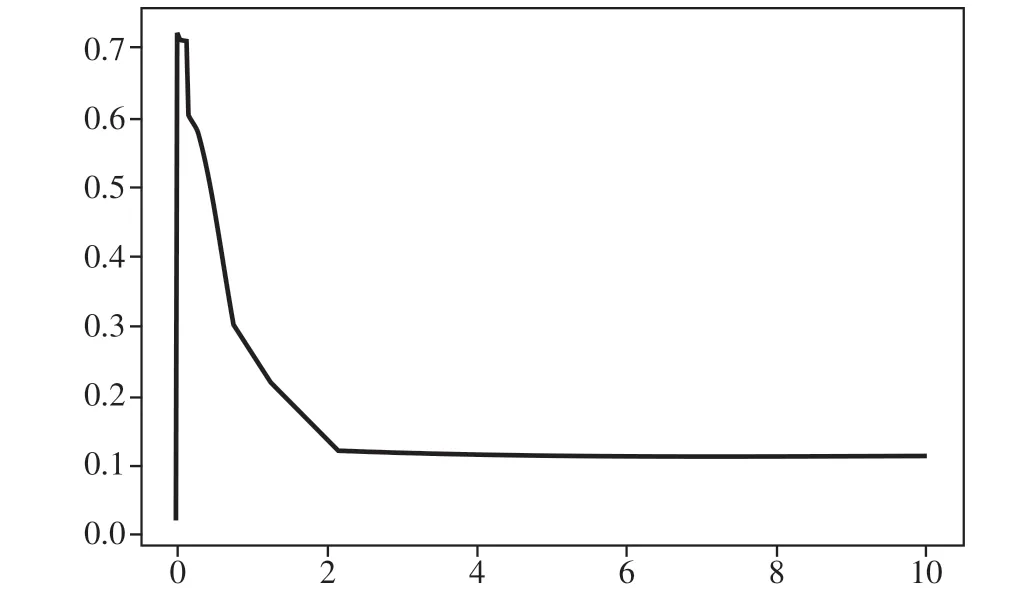
图12 rbf函数gamma值选优图
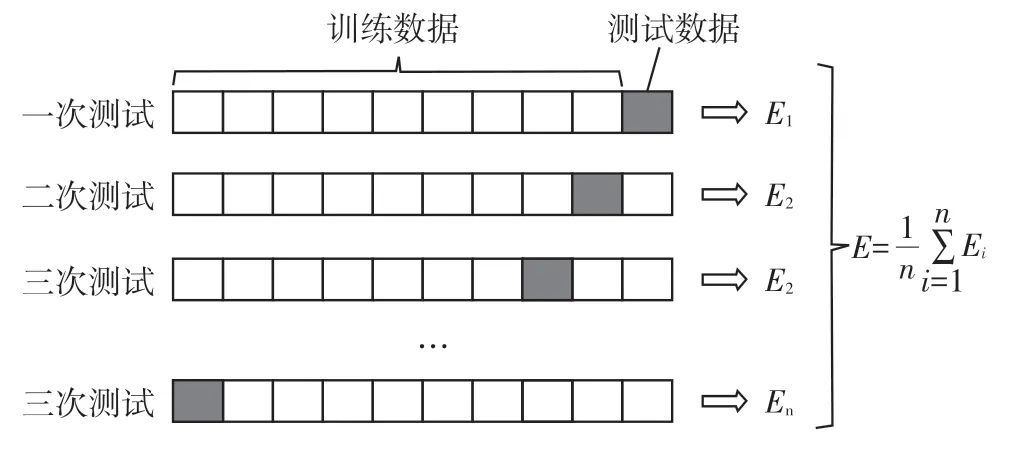
图13 交叉验证
3.2 结果
分别进行了不同次数的交叉验证,得出的模型准确率见表2。

表2 交叉验证次数-模型准确率 单位:%
由模型准确率知随机森林模型准确率最高最稳定。
4 结语
使用决策树、随机森林、支持向量机进行了疵点识别[13]的研究,通过理论分析和试验证实随机森林模型的准确率最高。机器学习算法的预测结果也存在着偶然性,为了获得更准确的结果,通过交叉验证,得到多个结果,取其平均值,这个均值更能代表模型的准确性[14]。试验结果表明,随着交叉验证次数的提高,3种模型的准确率都有所增加,但是增加到一定次数准确率反而降低了。决策树和支持向量机都不能达到最优,只有随机森林算法模型达到了最优。这是机器学习算法对不同数据集的不同体现。
未来工作一是引入图像预处理[15],减少计算量;二是丰富疵点数据集的疵点种类。

