基于互逆强化模型和数理统计方法分析专家评分偏差问题与建议

田林琳 孙维东 张弛 郭明 韦纳都

0 引言

作为引领科技发展的主要抓手之一,高技术研究发展计划(863计划)为提升中国整体科技实力和创新能力发挥了重要作用．“十二五”期间,863计划重点支持了先进制造、现代农业、海洋、地球观测与导航、生物和医药等技术领域中的前沿、关键、共性技术突破与核心技术产品及系统研发．众所周知的北斗羲和系统[1]、国际大科学工程——平方公里阵列射电望远镜(SKA)[2]等均受到其资助．该计划兼顾高科技发展和产业化应用,因而其不同技术领域均在一定程度上表现出研究范畴跨度大、技术纵深链路长、项目课题类别多的特色.

从科技计划管理角度出发,如何评估数以亿计的经费投入带来的产出价值是一个关键问题．对此,技术验收专家组的整体评价往往在实践中起着主导作用．而具备类似上述特色的科技计划涉及范畴广度、深度俱足,对验收专家的综合能力提出了严格要求．特别是在部分课题属基础研究、前沿探索类的情况下,其不确定性使课题成果和潜在价值难以客观衡量,既增加了专家评分难度,又令不同类型课题间的评分难以横向比较．因此,利用评分数据分析专家偏差,帮助科研管理人员评估专家评审能力,可以为了解领域创新成果和课题实施成效的评审信度与效度,以及更好地把握技术领域发展现状提供重要参考.

评审活动受到专业因素(如评分人是否充分了解参评对象属性)、心理因素(如评分人是否对参评对象心怀同情)、外部因素(如评分人是否与参评对象有利害关系)等多方面影响,因而评分偏差分析既是科研管理人员的关注焦点,也是心理学、应用数学和信息科学等学科的研究对象．20世纪末已有学者关注到地域科研实力评价中的偏差问题[3]．随后,一些科研管理人员对国家重点实验室评估偏差进行了分析,如谢焕瑛等从来源和成因上归纳了6种影响专家评分的效应[4]和4类偏差[5],张健等给出了应对潜在不公平评估的策略[6],杨晓秋梳理了实验室评估中的若干偏差问题[7],重点指出应增加专家培训力度使其更好地内化评估规则．这些研究主要是定性总结偏差成因和表现,但少有给出具体的定量分析方法．由于评委评分易受评分人经验知识、思考方式、人格特征等影响[8],心理测量学领域对评分偏差定量分析有很大兴趣,所用理论呈现出从经典测量理论[9]、概化理论[10]到现代测量学中的项目反应理论[8]的过渡．如著名的多面Rasch模型可用于评估项目难度、评委宽严程度、考生能力等参数及其交互关系,在结构化面试[11]、教育教学能力测试[10]、英语听说考试[12]等方面均有应用．但上述理论过于复杂,模型需较好的先验初始值进行迭代求解,且还可能出现不收敛现象[13]．忽略专业背景差异,专家评分与网购评分、书评影评评级等在形式上并无区别．随着互联网4.0时代到来,应用数学与信息科学学者聚焦于网络社区用户评分偏差和异常分检测,从数学和算法层面建立了评分评估模型与指标,同样可用于专家评分偏差分析．如Lauw等基于强化模型给出了衡量评分人偏差和参评对象争议性的两个指标[14],Dai等利用评分人和参评对象间的正面、负面效应建立二部图以检测行为异常的评分人[15],文献[16-17]则致力于面向众包系统构建评价体系和搜索高争议性参评对象．但需注意此方面研究更多是侧重于甄别异常用户以识别恶意或虚假评价．当然,也有少数专门面向评委评分偏差的研究,如吕书龙等利用假设检验等数学思想建立评分控制和偏差吻合模型[18],而文献[19]则基于投影寻踪构建评委综合评价模型.

考虑到心理学中相关理论限制较大,本文仅以数学和信息科学中的互逆强化模型和数理统计方法为技术手段，以863计划某技术领域课题验收为典型案例,对“十二五”期间863计划的评审专家评分偏差进行初步的定量探索．此项研究是对现阶段科研管理中专家偏差分析研究的完善与延伸,可助力精细化规范评审行为和后续专家遴选．据笔者所知,这是首次面向863计划等国家科技计划的专家分析工作.

1 偏差分析数据用例

863计划旨在面向经济社会发展需求加强技术研发和应用,同时也面向国际前沿和国家未来重大需求开展一定的前沿理论与技术探索,具有多学科交叉和兼顾研发与探索的特点．因此,其下设项目、课题的验收评审往往既要求专家组研发与集成经验丰富,又要求在领域前沿发展态势上具有敏锐的嗅觉．本文将“十二五”863计划某技术领域的课题验收评分作为偏差分析数据,一来便于科研管理人员将本文方法迁移用至其他技术领域;二来在科技体制改革后863计划被延伸融入到国家重点研发计划,两个计划间专家遴选范围重叠度较高,所得经验和结论可直接用在重点研发计划相应领域的重点专项中,帮助遴选合适的评审专家开展综合绩效评价工作．所用数据包含该领域全部专家评分,但由于项目数量较少且评价采用等级制,课题数量较多且评价采用百分制,后文对项目评级情况不做讨论．数据具体由252位专家对157个课题的1 135次评分组成,课题平均收到7.2个评分,专家人均评分4.5次,统计信息如图1所示.

课题接收评分频数图中可见各课题得分数量基本能保证分数均值、方差等统计信息的有效性．但对于专家给出评分的频数有两点说明:

1)863计划各技术领域均设有领域专家组,负责全周期跟踪项目及课题进展,从而能够较为完善地评价项目、课题完成水平,所以验收专家组一般由1～2位熟悉相应执行情况的领域专家组成员和同行专家共同组成．从专家给出评分频数图可知,随着评分次数增加,人数快速下降,自左到右从同行专家居多转为领域专家组专家居多.

2)对于评分次数较少的专家难以确保其评分信息有效性,下文研究仅聚焦于至少有5次评分的74位专家．虽然无法分析剩余专家评分,但这些专家给出的分数仍然有助于课题评价,在对课题情况开展分析时仍将使用全部专家评分数据.

2 评分偏差评估模型与指标

2.1 评分偏差成因与类型

近十几年来,不同科研管理人员根据各自经验总结了科研活动中的评分偏差成因与类型．表1列出了其中比较有代表性的看法,从中不难发现:

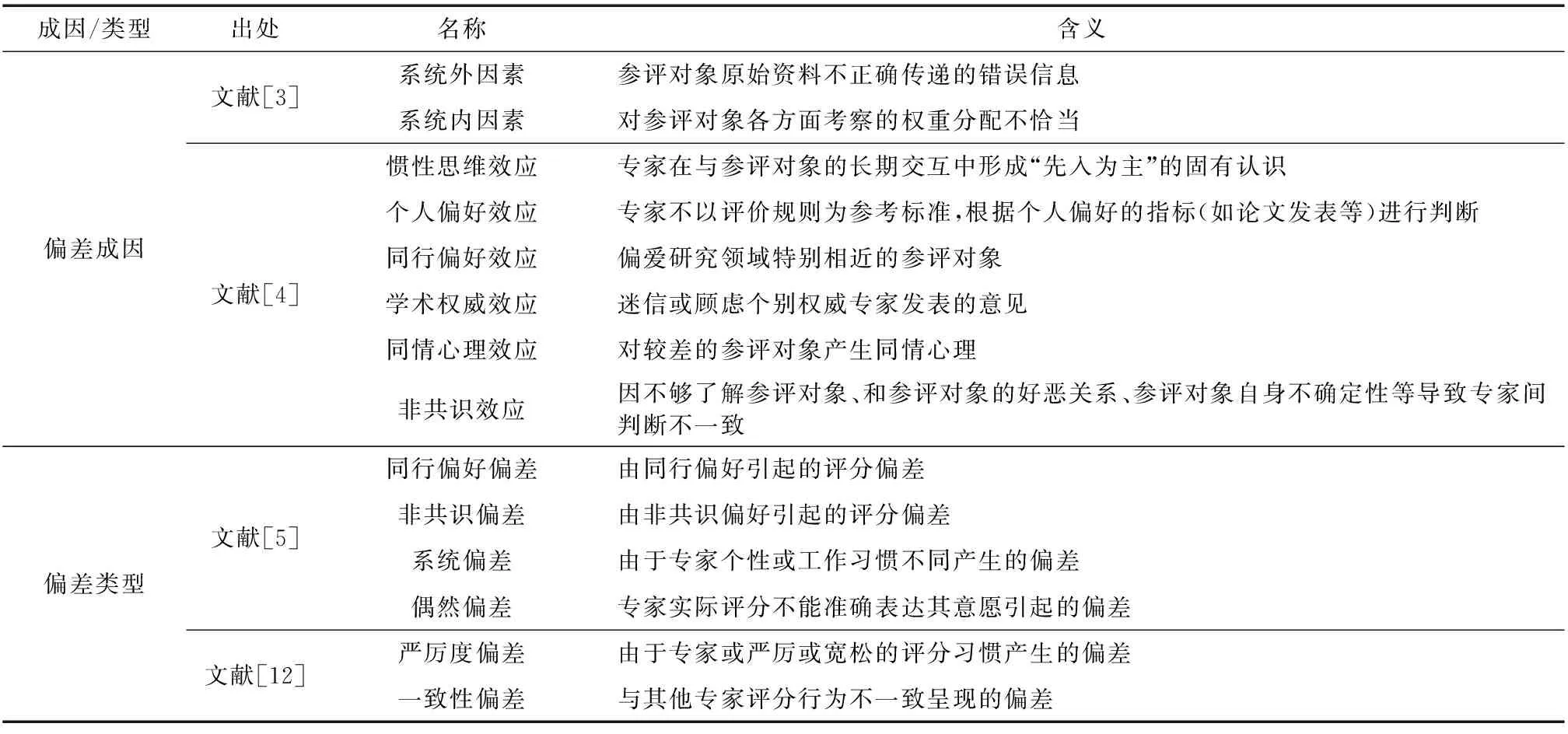
表1 科研评分偏差典型成因与类型Table 1 Typical causes and types of scientific research score bias

1)系统内、外因素来自专家和课题之外,超出了本文范畴;偶然偏差较小且属于量化评分中必然出现的正常偏差[5];同行偏好偏差、非共识偏差源自同行偏好效应和非共识效应,可以一并讨论．故下文不再展开这些内容.

2)惯性思维、学术权威和个人偏好效应难以仅凭评分数据进行分析．不过遴选同行专家的回避原则显著降低了专家与课题间的关联性,一定程度上避免了其影响．此外,前两者在验收评审中未必会增加偏差:由于长期跟踪课题,惯性思维使领域专家组成员评分更可靠;专家的权威性反映了其卓越的专业素养和眼光,权威效应也可能缩小偏差.

3)同行偏好属于普遍性偏好,对绝大部分专家的作用是均衡的[5],对于课题间评分的相对影响不大.

4)各课题验收专家均为相关方向资深同行且符合回避原则,不能了解参评课题及同课题间存在好恶关系的可能较低，但部分课题的前沿性和探索性增加了量化评价难度,可见验收评审中的非共识效应由课题不确定性主导．为明确这一点,以下将因不确定性引起的非共识偏差归于课题而非专家,并称之为争议性偏差[14,17].

5)因个人习惯导致评分尺度不同,从而产生或偏高或偏低的系统性差异,所以系统偏差和严厉度偏差非常相似．另外,同情心理是形成个人评分习惯的潜在心理因素,该效应令专家倾向于高估课题分数．因此,本文将同情心理效应引起的偏差归于上述偏差,并将其统称为专家固有偏差.

6)评审活动中无法知悉体现课题完成情况的真实分数,但合理的假设是多数课题评分或其均值是较为客观和接近真实值的,所以在评价专家评分能力时实质上往往是综合参考对同一课题的其他专家评分进行判断,也即暗含了对一致性偏差的考察.

综合以上分析可知：课题争议性干扰了专家评分准确性,需在评估专家偏差时降低其影响;与其他专家评分的一致性体现在评估专家总体偏差的过程中;固有偏差代表了专家间评分松紧尺度的不同标准;除系统内、外因素和偶然偏差等不在本文范畴或可忽略的因素之外,个人偏好等因素既难以通过评分数据辨别,在课题评分中又仅对个别专家产生较大影响,本文将它们引发的极端评分不加区别,统一归于异常评分．综上,下文将结合评分一致性和课题争议性两方面建立专家总体偏差评估模型,并利用两个假设检验方法实现对异常评分和固有偏差的检测,以此开展专家评分偏差分析工作.

2.2 基于互逆强化的总体偏差评估模型

设有n个专家参与m个课题的评分工作,目标是评估各专家的总体评分偏差．若已知全部评分的真实偏差,经简单聚合操作就可以得到专家总体偏差,如用均值作为第i个专家的总体偏差:

(1)

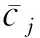
(2)

此时问题转为如何衡量课题争议程度．争议度是引发专家间出现非共识和意见发散的能力,最直观的衡量方法就是对此课题接收的全部评分求偏差均值．但同样要考虑参评专家的评分能力,因此令课题争议度为

(3)

式(2)和(3)说明了专家偏差和课题争议度的相互依赖,争议度影响着专家偏差,专家偏差又反过来影响争议度,二者联合构成了互逆强化模型[14]．如果把专家和课题视作顶点,把评分视为顶点间连边的权重,上述问题将转为常用于社区网络信息挖掘的特殊二部图[20]．本文定义i对j的评分偏差为i的评分与其他专家对j的评分之差的绝对值平均,有

(4)

式(4)中eij为i给j的分数,nj为给课题j评分的专家数,在验收评审中nj必然大于1,故式中分母必为正整数.

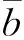
B=K(1m-C),

(5)

C=LT(1n-B),

(6)

式(5)、(6)中的1分别表示长度为m和n的全1列向量,K和L为n×m大小的矩阵且i行j列元素分别为Kij=dij/mi和Lij=dij/nj．mi类似nj的定义,代表专家i评审的课题数．上标T表示矩阵转置.

互逆强化是全局性的动态过程,因为变动任何课题的争议度估计值会影响给其评分的专家的偏差估计,偏差估计值变化又会影响这些专家给予分数的课题的争议度估计,形式上相似于概率图模型[21]中的信念传播机制[22]．借鉴谷歌的PageRank排序算法[23],Berkhin等得到了B和C各自的自嵌套表达式,经自迭代求解出B和C．然而,这一求解方式需满足一定前提且在自迭代过程中要周期性规范化B和C．此外,笔者发现将自迭代得到的B代入式(6)计算出的C,与自迭代得到的C并不一致,反之将自迭代结果C代入式(5)也有相似的现象,这是与总体偏差和争议度的相互依存关系相违背的．因此,本文采用互迭代方式进行求解,即先在(0,1]区间随机初始化B为B0并代入式(6)得到C为C1,再将C1代入式(5)更新B为B1,如此往复直至收敛．当然,从初始化C开始互迭代可得到相同结果．以上方法虽然简单但非常有效,可以证明互迭代过程同样能收敛．证明如下:

不妨设任意第k至k+2轮迭代中得到Bk,Bk+1和Bk+2,则有

Bk+2-Bk+1=K(1m-Ck+1)-K(1m-Ck)=

KLT(1n-Bk)-KLT(1n-Bk+1)=

KLT(Bk+1-Bk)

(7)

收敛即要令Bk+2和Bk+1中对应元素变化不大于Bk+1和Bk间变化,利用向量l2范数‖·‖2可等价转换为满足‖Bk+2-Bk+1‖2≤‖Bk+1-Bk‖2．引入变量Uk+1=(Bk+1-Bk)(Bk+1-Bk)T,有:

tr(Uk+2)-tr(Uk+1)=

tr(KLTUk+1LKT)-tr(Uk+1)=

-tr((I-LKTKLT)Uk+1)=

-tr(RUk+1),

(8)

其中tr(·)为矩阵的迹,I为单位矩阵,R=I-LKTKLT.

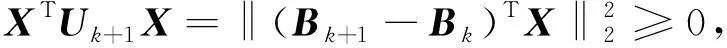
1)Bk+1-Bk不为零向量:Uk+1相应为对称正定矩阵．存在可逆矩阵P和Q,使R=PTP和Uk+1=QTQ,则Q(RUk+1)Q-1=(PQT)TPQT,即RUk+1与(PQT)TPQT相似,二者的迹相等．显然PQT可逆,从而知(PQT)TPQT是正定矩阵,其迹大于0．因此有tr(RUk+1)>0,故从式(8)易知‖Bk+2-Bk+1‖2≤‖Bk+1-Bk‖2成立.

2)Bk+1-Bk为零向量:此时‖Bk+2-Bk+1‖2≤‖Bk+1-Bk‖2成立.

综上得证互迭代使B稳定收敛,同理可证C的收敛性．实际上,只要B没有恰好初始化为收敛解,B1-B0不会是零向量,随后B将不断更新直至收敛;而若恰好初始化为收敛解,则无需迭代已得到了想要的结果．本文在评分数据上基于不同初始值多次求解,均经3～4次互迭代即可得到稳定且一致的结果.

2.3 基于假设检验的异常评分与固有偏差检测

异常评分反映了专家评分因某些主客观因素引起的明显偏离真实分数的现象,了解异常评分情况有助于识别问题专家．同一课题的评分数据是以真实分数为中心的随机变量,如能保证专家评分客观性,该变量将近似服从高斯分布．参照文献[18],本文以课题均分作为真实分数的近似,视均值上下2倍标准差范围为评分正常区间,以此判断专家评分是否异常并统计各专家的异常评分次数．如对于专家i给出的课题j评分,

Ni←Ni+1, ifeij∉[μj-2σj,μj+2σj],

(9)

其中,Ni为专家i异常评分次数,初始为0;eij同前为专家评分;μj和σj分别是课题j平均分和标准差,根据该课题收到的所有评分计算．依验收规范应先剔除最高分和最低分后再计算平均分,但考虑到部分课题参评专家仅6人,剔除后无法保证统计稳定性,所以本文没有剔除最值．此外,文献[18]与本文不同,其不合理地对各课题采用统一标准差,会导致低争议度课题的异常评分漏检和高争议度课题的异常评分虚警.

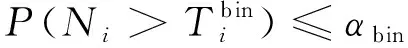
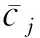
(10)

近似服从t分布t(mi-1),式中μfi和σfi分别为加权偏差向量的均值和标准差．同时,得到了两个对立假设:零假设(专家i评分无固有偏差)和备择假设(专家i评分有固有偏差)．给定显著性水平αt后,从t分布表确定双侧阈值t1-α/2(mi-1)和tα/2(mi-1)．超出阈值即可判定该专家明显存在固有偏差:titα/2(mi-1)说明评分过于宽松,倾向于给高分.

至此,本部分已给出评估专家评分偏差的3个指标及衡量课题争议度的指标．其中：总体偏差是对专家偏差的整体性估计;异常评分检测极端值,是对偏差的突变性估计;固有偏差判断专家内在的评分尺度习惯,是对偏差的倾向性估计．三者间有着一定联系:

1)异常评分次数和固有偏差信息既相互影响又相互补充:固有偏差在极端情况下会引发异常评分,且异常分数将一致性地极高或极低;反过来,异常分数过多同样可能增加固有偏差．当然,因为异常评分受多种因素影响,更常见的是异常分数中同时包含高分、低分,不会引起固有偏差．这些可能的情况无法单独从异常评分或固有偏差来判断．因此,这两个指标既从不同侧面反映专家的特定偏差问题,又在特定情况下表现出一定耦合性.

2)总体偏差与异常评分、固有偏差粒度互补:总体偏差是从整体层面评估专家偏差的核心指标,涵盖了突变性、倾向性等考量．这对于从粗粒度快速锁定问题专家非常关键,但无法判断问题具体信息,如专家偏差主要受外部条件干扰,抑或评审规范不够内化,还是评分尺度异于他人?这些细粒度信息对于采用何种处理措施很有指导性,可通过异常评分和固有偏差来判断,必要时还可继续搜索其他相关信息进一步定位问题.

综上所述,3个指标相结合才能较完善地分析专家偏差,下文将据此完成对863计划某领域课题验收专家的偏差分析.

3 评分偏差评估结果与分析

3.1 评分偏差评估结果

本文所用数据涉及157位专家对252个课题的评分,课题平均分和标准差如图2所示．课题82得分最高(95.17分),课题96得分最低(73.18分),标准差在0.7～7.55间波动,表明这些课题无论在完成水平还是在争议性上均有很大差异,尤其后者会干扰评审评分,在评分偏差分析中将其纳入考量很有必要．因本文聚焦于专家偏差,下文对争议度不做详细讨论.

使用2.2和2.3中方法面向评分不少于5次的74位专家进行偏差评估,得到各项指标及阈值如表2所示(显著性水平0.01)．表2中序号对应总体偏差排名,序号越小意味着总体偏差越大．由于我们仅展示了3位小数,导致少量序号不同的专家总体偏差值看上去相同,如专家19～21．为使估计值均匀分布在[0,1]以方便相对比较,所列总体偏差经过了最大值规范化处理．因空间有限,表2中只给出了t检验的右侧阈值,左侧阈值为其相反数.

表2中斜体加粗的部分为异常评分次数大于或等于阈值以及t检验值超限的数字．7位专家异常评分过多,仅占专家总数9.46%,且其中6位次数刚好等于阈值,可认为专家整体低异常;14位专家出现固有偏差,占比略高,约为18.92%．但其中多数专家检测值超限不多,造成的实际高估或低估偏差分值不大(具体见3.3中专家实例),说明专家整体固有偏差程度是可以接受的．另一方面,异常评分过多的专家序号均靠前,并且总体偏差最大的正是唯一超过异常次数阈值的专家,侧面证明了总体偏差指标的有效性．然而固有偏差较大的专家呈不规律分布,原因在于固有偏差表示评分会习惯性的偏高或偏低,意味着评价课题完成情况的专家给分尺度不同,大多数情况下并不会引起极端评分和高总体偏差．但大部分专家评分仅有5～7次,过多的异常评分引起总体偏差显著增加是很正常的．当然,过大的固有偏差仍然会对总体偏差产生不可忽略的影响,如排名第8位的专家．以上现象均印证了2.3结尾部分的推测.

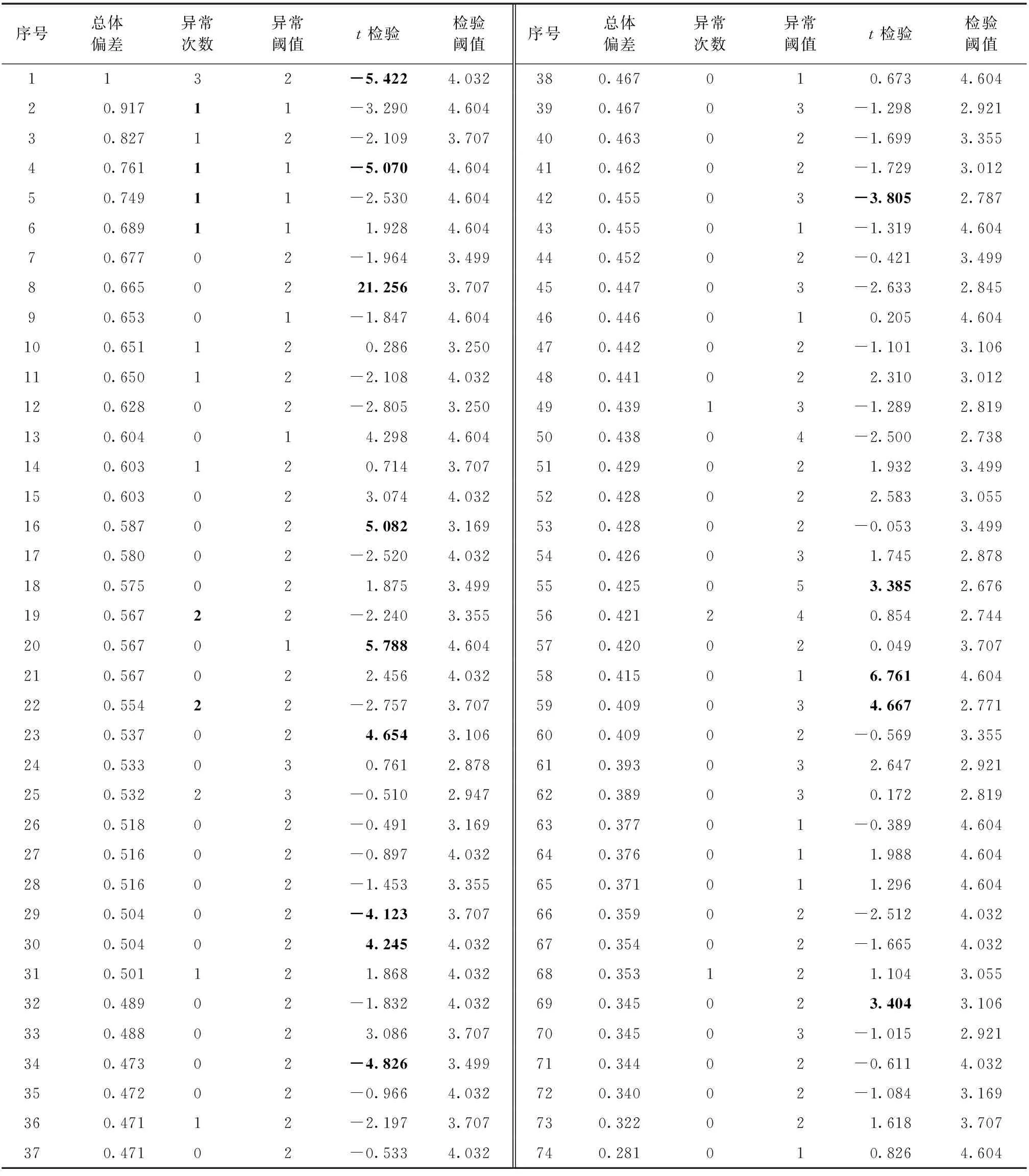
表2 专家评分偏差指标值及相应阈值Table 2 Index values and corresponding thresholds for expert score bias

3.2 总体偏差模型互迭代结果验证

原始互逆强化模型需将偏差向量B和争议度向量C表示为递归形式后,分别自迭代求解．自迭代过程中对B和C的规范化会导致求得的结果丢失式(5)和(6)中体现的交互关系,但模型的构建依赖于B和C的耦合性．这种矛盾并不合理,所以本文提出了互迭代策略作为替代．为验证互迭代的求解效果,本部分分别采用这两种方式得到专家总体偏差和课题争议度,结果如图3—5所示.

利用自迭代分别得到总体偏差B和争议度C,同时基于相互依赖关系,也可将自迭代结果B代入式(6)得到相应的C,同理式(5)又可用自迭代结果C得到相应的B．理论上,这两个B和两个C之间应该是一致的,但从图3易知实际情况并非如此．周期性规范化处理导致无法定量比较,故图3中对比的是自迭代结果排序情况．图中横轴表示直接求解结果的排序,纵轴为将自迭代结果代入式(6)和(5)的计算结果排序,排序越一致则散点越接近对角线．可以看出偏差排序差别巨大,争议度排序略好但仍呈现出明显发散状.

利用本文的互迭代方式得到B和C,同样可按照上述过程再次利用两式反算出C和B．图4给出了这些结果的对比结果,互迭代结果间表现出了高度一致性．最后,图5展示了不同求解方式的结果排序对比,横轴为自迭代直接得到的B和C排序,纵轴为互迭代结果排序．可知,基于两种求解方式的排序基本相同,尤其是排名靠前的部分,而排序不同之处均为小幅差异,对于专家偏差分析影响非常小．但考虑到互迭代方式始终维持着总体偏差和争议度间的关联性,本文提出的求解思路明显更加合理．此外,互迭代的另一个优点是无需引入规范化处理,从而结果可定量比较,因此只有图4中直接展示了总体偏差值和争议度值而非其排序,更利于科研管理人员后续开展更精细的分析工作.

3.3 代表性专家实例分析

如前文所述,3个偏差指标各有侧重,相互结合才能较好地分析专家偏差情况．本部分以几个专家实例分析一些有代表性的偏差表现,同时也验证本文所用指标的有效性．首先是表2中的第1位专家,其总体偏差最大且是唯一异常评分次数超过阈值的专家．此外,通过t检测认定该专家有给低分的习惯．图6给出了其评分数据和相应课题平均分,其中柱状分数为专家1参评的课题平均分,折线为专家1的评分．注意图中误差棒以±2倍标准差为上下限,以便快速确定异常评分位置(后续图7—9采用相同设置)．图中折线一直处于平均分以下,在课题107、108、110处出现评分异常,其余3个课题中评分也逼近了下限．特别是对于评分波动性较大的课题108,专家1评分仍能超出正常范围．过多的异常评分和明显的固有偏差集中体现为极大的总体偏差,这表明该专家问题严重,在后续评审活动中不建议将其继续作为技术专家.

总体偏差同样较大是专家8,从固有偏差检测结果知其具有很强的给高分习惯,但未有异常评分.

在图7中专家8表现与分析一致,评分全部高于平均分且处于正常区间的较高位置．但对于分数波动较大的课题108,该专家给出了较为合理的评分,这是一个比较好的现象．评分尺度过于宽松是专家8总体偏差较大的主导因素,证明了固有偏差过大时也会对总体偏差产生严重影响,但这种“尺子”方面的问题仅从总体偏差无法发现,说明了结合固有偏差和总体偏差的必要性．与专家8相反,从表2和图7中均能确定专家58也有给高分的倾向,但程度更低，从而总体偏差较小,仅排在第58位．仅以t检验结果而言,有明显固有偏差的专家分布在表2排序的各部分,表明固有偏差在整体上对专家总体偏差的影响还是可以接受的.

与固有偏差不同,异常次数的多少和总体偏差的大小显著相关,表2中异常次数达到阈值的专家均在排序前列．原因在于专家评分次数普遍较少,集中在5～7次,所以每个异常值的出现均会对总体偏差有不小贡献．例如专家6总体偏差较大而t检测值低,从图8中也可看出仅有轻微的给高分倾向,但5次评分中就有1个异常值．当然,也并非异常评分少且无明显固有偏差就意味着总体偏差小,原因有二:一是即便没有或较少出现异常评分,还可能存在较多接近但未超出正常范围的评分;二是固有偏差不明显也可能是因为评分忽高忽低,如图8中显示的专家10评分情况．该专家参与了10次验收评审,仅1次评分异常(相应阈值为2次),t检验值0.286接近于0，表明其无过宽或过严的评分惯性．但从图8中可知其评分在平均分上下波动,并且过半评分接近正常范围上下限,故偏差排序靠前．对于类似表现的专家,仅凭异常评分和固有偏差检测是不够的,加入总体偏差才能正确分析其偏差情况.

在分析了5个存在问题及表现各不相同的实例后,图9给出专家72的评分及相关课题分数信息,作为较理想的专家示例，其总体偏差极小、无异常评分,仅评分尺度略显严格,图中也可看出该专家评分与平均分非常一致.

3.4 专家评分偏差归类

以上结合典型实例分析了3个偏差指标的关联性:异常评分体现突变性信息,对总体偏差影响明显;固有偏差体现一致性的评分倾向,对总体偏差有一定影响;总体偏差是综合性评价,既包含了突变性和倾向性信息,又体现了两者之外的一些因素,但不能细致区分偏差表现．分析工作应先根据总体偏差大体锁定问题专家群体,再联合异常评分、固有偏差判断专家具体问题并确定处理措施．因此,表3列出了以这3个指标划分的8种专家偏差类型及建议的应对措施.

异常评分次数和固有偏差均有检测阈值．为了使总体偏差保持一致,本部分简单采用大津法[24](又称最大类间差方法)寻找可将总体偏差分为差距最大的两类的阈值,这样即可利用3个指标的阈值将任一专家归类到特定偏差类型．根据大津法得到高总体偏差专家(排序1～21)和低总体偏差专家(排序22～74)．各类型专家人数和占比也列于表3．这些偏差类型不限于本文数据,在其他科技计划管理活动中同样可以应用.

表3 专家评分偏差类型及应对措施Table 3 Types of experts according to their score biases and countermeasures

对于部分专家需进一步培训和沟通,有针对性地矫正评分行为．对建议措施解释如下:

1)Ⅰ类专家严重影响评分可靠性,不建议继续参与验收评审.

2)Ⅱ类专家总体偏差大、异常多、评分忽上忽下,可以推断频繁受外在因素干扰且影响程度较大(如与课题团队间的好恶关系、不正确的刻板印象等)．主要问题在于评分独立性、客观性不足,应加强此方面意识培训．此外还应观察其t检验值是否已接近阈值,预防Ⅱ类专家转为Ⅰ类.

3)Ⅲ类专家评分尺度问题明显,或偏高(如受同情心理效应影响)或偏低(如有高标准、严要求的评审习惯)．较大的总体偏差表明该问题已明显影响到评分合理性．应多与此类专家沟通,令其加强尺度把握.

4)Ⅳ类专家偏差大但其他指标正常,说明其评分上下波动却没有过于极端．推测此类专家的主要问题在于对评分标准理解不足而非受外在因素的严重干扰,应加强培训提高验收规范内化程度．此外,也存在评分次数不多使异常评分和固有偏差检测不准确的可能,仍需跟踪观察确定其是否为潜在的Ⅰ/Ⅱ/Ⅲ类专家.

5)Ⅴ类专家仅为保证完整性而提出,基本不可能出现．原因在于异常评分多、固有偏差强均会增加总体偏差,极难同时出现低总体偏差．本文数据一定程度上证明了这一点.

6)Ⅵ类专家与Ⅱ类成因相似但程度较轻,是在评分次数较少的专家中存在的小概率情况．因其偏差较小,不建议采用强化培训,应先进一步搜集相关信息确定外部因素来源后,提醒专家注意该因素影响.

7)Ⅶ类专家仅固有偏差偏高,提醒其稍微注意控制评分尺度即可.

8)Ⅷ类专家各项指标正常,无需任何处理措施.

需要注意的是,以硬阈值划分总体偏差只是一种粗略的分组方式．阈值附近的高、低偏差专家客观上并无太大区别,不能粗暴地认定前者一定有严重问题而后者没有．表3仅是给出了一些参考措施建议,对于接近总体偏差阈值的专家应根据情况具体讨论．雷达图因其形状的规律性和对比的便利性在分析偏差效应中非常适用[5]．本文给出了部分偏差类型的理想雷达示意图和相应实例,可以看出雷达图非常形象地表达了类型间的不同特点.

雷达图根据专家评分与课题平均分之差绘制,越外层的多边形表示高估越严重,越内层则越低估．角点上的数字代表课题序号,同一多边形的边构成了特定差值的等值线,差值列于多边形左上位置,红色点代表异常评分．对于专家实例,雷达图中显示范围统一为-16～16，便于公平比较．突变性的异常评分会造成雷达图中形状的不规律变化．对于涉及异常评分较多的类型,尤其是可能既有高异常分又有低异常分的情况(Ⅱ和Ⅵ型),并没有理想的雷达示意图可代表其多样性表现．即便异常评分少,但若总体偏差高且无明显固有偏差(Ⅳ型),评分仍然是围绕课题平均分在较大范围内上下波动,同样难以找到理想示意图．排除掉以上三类和近乎不可能的类型(Ⅴ型),图11—13展示了Ⅲ、Ⅶ、Ⅷ三种类型．另外,同时满足异常评分多和固有偏差强的条件下,异常评分或者多为极高分、或者多为极低分,不规律性显著降低,所以Ⅰ型也可找到理想雷达示意图(图10)．从图10—13可知,专家1(偏差大、异常多、偏低估)、专家8(偏差大、异常少、偏高估)、专家58(偏差低、异常少、偏高估)、专家72(偏差低、异常少、固有偏差弱)与相应类型的理想雷达图非常相似,说明这4种偏差类型确有稳定的雷达图形状．即便不采用本文的3个指标,科研管理人员也可利用雷达图直接完成简单的偏差分析工作,至少能够快速找到理想专家群体(Ⅷ型)以提高评审结果可靠性,或者找到Ⅰ型专家群体减少其参评次数甚至不再作为专家人选.

4 总结

在科技管理工作中,验收评审有着评估课题完成水平、衡量科研产出价值的重要作用．开展评审专家可靠性研究对于科技评审活动是十分有指导意义的．因此,本文结合数据挖掘算法和数理统计方法给出了衡量专家评分偏差的3个定量指标,以对“十二五”863计划某技术领域课题验收专家的评审行为进行初步探索．分析发现,该领域验收专家评分整体合理,仅1人次评分异常明显;固有偏差处于可接受范围．本文还根据偏差指标进一步归纳了8种偏差类型并给出应对措施建议,此项研究是对现阶段科研管理相关工作的完善与延伸．科技部近期正在开展“十三五”国家重点研发计划各重点专项首批到期项目的综合绩效评价,分析结果可用于绩效评价专家遴选和评前培训,帮助特定专家群体内化评审规范并降低评分习惯、个人偏好、外部因素等影响．此外,文中采用的评价体系和专家偏差类型同样可在其他科研管理活动中发挥评价评审过程、规范评审行为的作用．为响应“三评”(项目评审、人才评价、机构评估)改革意见[25],下一步工作将聚焦推进本文评价体系在多项国家科技计划乃至各类“三评”活动中的推广应用．一来从专家偏差性和评审对象争议性两方面综合评价评审过程、完善评审机制,同时广泛采样检验本文分析方法的泛化能力;二来基于总体偏差、固有偏差和异常评分并结合大量评分数据,既可以从不同粒度归纳总结专家潜在的共性问题和分析差异化的评审行为,又能根据所得经验和专家历史偏差评价结果辅助“三评”专家遴选工作,提升科技评审效度．正值教育部、科技部联合印发《关于规范高等院校SCI论文相关指标使用 树立正确评价导向的若干意见》[26]之际,希望本文能够对其中的“完善学术同行评价”、“规范各类评价活动”等内容提供方法论支撑.