权重平衡有向网络下分布式约束优化的连续时间算法设计
朱亚楠 温广辉
0 引言
在过去的几十年里,多智能体系统的分布式协调问题因其在工程、自然、社会科学等领域的广泛应用,已有大量的研究成果.分布式优化作为多智能体系统中的一个重要协调问题,其目的是多智能体通过与邻居之间的相互协作实现整个网络最优决策.在分布式优化问题的求解方面,早期的工作主要基于迭代格式的离散时间算法.比如,Nedic等将多智能体一致机制和优化方法相结合,分别设计了用于求解无约束优化和凸交约束优化的分布式次梯度算法和分布式次梯度投影算法[1-2].另外,文献[3-8]建立了求解等式或不等式约束优化的分布式离散时间优化算法.
由于连续时间系统在算法设计和分析方面的优势,基于连续时间系统的分布式优化算法设计近年来受到了研究者的广泛关注.针对无向网络下无约束分布式优化问题,文献[9-10]分别设计了基于零梯度和一致性和基于牛顿-辛普森一致性的连续时间算法.文献[11-12]针对权重平衡有向网络下无约束的情况,从原始对偶的角度出发,分别提出了基于鞍点动力学和基于负反馈梯度流的连续时间算法.为了消除参数对全局网络信息的依赖性,文献[13]提出了一种自适应的连续时间算法.通过结合估计左特征向量的一致性协议和权重平衡有向网络下的连续时间算法[12],文献[14]进一步给出了权重非平衡有向网络下的连续时间协调算法.相比较无约束的情况,约束优化问题在实际中的应用更加广泛[15-20].考虑到多个局部约束交的情况,文献[15]设计了基于二阶多智能体系统的分布式优化算法.为了避免上述工作中乘子变量的无界性,文献[16]进一步提出了基于原始对偶的连续时间算法.此外,文献[17]采用神经网络动力学求解局部等式和不等式约束的分布式优化问题.最近,文献[18-20]研究了同时包含局部等式、不等式和闭凸集约束的分布式优化问题.对于更多的分布式优化算法的工作,读者可参考一些文献综述[21-23].
从上述的工作中可以发现,分布式约束优化问题的连续时间算法设计主要针对无向网络.在有向网络下,智能体之间的信息交互往往是不对称的,这也导致无向网络下基于对称拉普拉斯矩阵的算法通常不再适用有向网络的情况.因此,有待进一步探讨有向网络下约束优化问题的连续时间算法设计.本文考虑一类带有局部闭凸集约束的分布式优化问题,其中网络的全局目标函数由智能体的局部目标函数的和构成.目的是在权重平衡有向网络下,智能体分布式合作找到该问题的全局最优解.对于该问题的研究,文献[24]给出了基于Fenchel对偶梯度的离散时间算法,该算法的详细收敛性分析在文献[25]中给出.由于获得Fenchel对偶梯度仍需要求解最优化问题,因此很难在迭代中直接使用Fenchel对偶梯度.为此,本文从不精确的Fenchel对偶梯度出发,结合一致性机制,提出一类基于奇异摄动系统的分布式连续时间算法.针对所提出的算法,结合凸分析和Lyapunov稳定性理论,对所提算法进行收敛性分析及数值仿真验证.
1 预备知识
本节给出论文中使用的数学符号、代数图论及凸分析中的相关概念和理论预备知识.
1.1 符号说明
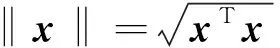
1.2 代数图论
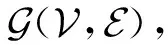

1.3 凸分析

根据投影的定义,可得如下不等式:
(u-PK(u))T(v-PK(u))≤0,∀u∈Rn,v∈Rn.
(1)
2 问题描述
考虑一组多智能体求解如下分布式优化问题:
(2)

为求解优化问题(2),做出如下假设:
假设1

注1假设1保证了问题(2)解的存在性和唯一性.
假设2智能体之间的有向通信网络满足强连通且权重平衡性.
3 主要结果
本节首先将问题(2)转化为等价形式,然后从等价形式的Fenchel对偶问题出发,设计一类基于奇异摄动系统的分布式连续时间算法.最后,对所提算法进行了详细的收敛性分析.
3.1 Fenchel对偶问题
问题(2)等价为
(3)
(4)
其中w=col(w1,w2,…,wN).
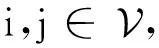
等价地,
进而,当w*是问题(4)的一个最优解时,可得
是问题(2)的最优解.
(5)
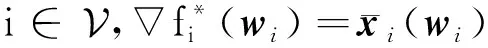
3.2 算法设计和收敛性分析
(6)
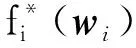
(7)
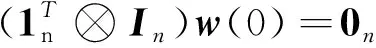
(8)
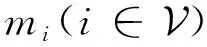
证明记col(x*,w*)为系统(7)的一个平衡点,则可得
(9)
(L⊗In)x*=0Nn.
(10)
注意到
因此,
则在变量y和w下,可重写系统(7)为
(11)
考虑如下的Lyapunov函数:
则V关于系统(11)的导数为
其中
由投影不等式(1),可得不等式:
由f的强凸性,f的Lipschitz连续性及引理2可分别得:
注意到
根据引理1中的(Ⅱ)可知成立不等式
λ2‖e‖2-eT(L⊗In)y+
(12)
(13)
因此,
(14)
再次利用f的强凸性和f的Lipschitz连续性可得:
结合f*(w)≥f*(w*),有
(15)
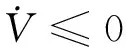
f*(w)-f*(w*)≥(f*(w*))T(w-w*)+
4 数值仿真
本节给出一个数值例子验证所提算法的有效性.考虑由5个智能体构成的通信网络如图1所示.智能体的局部目标函数和局部闭凸集约束给定如下:
f1=(x-1)2+e0.5x,f2=(x-4)2,f3=x2,
f4=x2+e0.1x,f5=x2+e-0.1x,
Ω1=[-1,1],Ω2=[-2,2],Ω3=[0,2],
Ω4=[-5,1],Ω5=[0,3].
在这个优化问题中,可以计算出m=2和M=2+0.25e0.5.图1中的通信网络的Laplacian矩阵
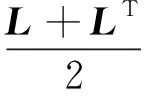
5 结论与展望
为求解权重平衡有向网络下分布式凸交优化问题的最优解,本文从其等价问题的Fenchel对偶问题出发,将投影方法和一致性机制相结合,设计了基于奇异摄动的分布式连续时间算法.然后,结合凸分析方法和Lyapunov稳定性理论证明了所提算法的收敛性,并从数值仿真进一步验证了算法的有效性.本文仅考虑了有向网络为权重平衡的情况.未来将进一步探讨权重非平衡网络下分布式约束优化的连续时间算法设计.

