石材幕墙连接计算对比分析

(上海富艺幕墙工程有限公司，上海 201617)

0 引言

石材作为外墙和装饰材料历史悠久，以其独特的纹理和质感备受青睐。尤其是当代石材幕墙发展迅猛，应用范围十分广泛，建成了各类特色建筑。基于社会发展需求，近年来石材幕墙高度已突破规范要求用于高层建筑，过程中也出现不少安全问题，石材面板坠落事件时有发生，故其安全可靠性受到广泛关注。石材密度大板块重，挂点承受自重大。基于天然材料的特性，材质离散型较大[1]且细微裂纹难以发现。另外，石材属于脆性材料，挂件处局部强度是石材防坠落安全保证的基础。

本文针对石材幕墙的以上特点及现状，结合规范、材料力学公式和ANSYS WORKBENCH有限元对石材幕墙槽口连接进行对比分析[2]，确定设计中的薄弱环节，指导工程实践，保证设计的合理、安全。分析研究的切入点是，按石材幕墙传力方式，对石材槽口、金属挂件两个部位进行局部强度分析，采用公式计算和有限元两种方法对比，分析其结果差异性并提出合理化建议。

1 石材槽口强度分析

目前石材幕墙挂件连接主要分为铝合金短槽与背栓。早期的钢销及蝴蝶码连接方式已被淘汰，而通槽系统在工程中使用极少。背栓系统可靠度高，但由于造价偏高，只能根据市场情况综合考虑采用。故工程中广泛采用的是铝合金短槽系统。

一般面板采用上下短槽连接，共4个连接点（即4个短槽）。由于不像玻璃、铝板等面板四边支撑，石材幕墙面板属于点支撑，支撑连接部位搭接面积小，局部应力集中明显，尤其是开槽后受力更为复杂，导致短槽石材挂件部位强度是石材幕墙最薄弱处，是石材幕墙安全最关键的控制点。

按照规范要求，石材槽口部位仅需要验算剪应力，而挂件并非直接作用于槽口根部，即挂件作用点到计算截面有偏心，故槽口部位必然产生弯矩，弯曲应力也应予以校核，脆性材料按第一强度理论控制第一主应力。

现以上海某项目为例，对石材槽口部位抗剪、抗弯进行对比。风荷载地面粗糙度取B类，高度25m，角部区域风荷载体型系数us=1.6，花岗石厚度30mm，板块分格宽×高为1.0m×0.6m，挂件系统如图1（竖剖）、图2（横剖），开槽方式见图3，槽口布置见图4。

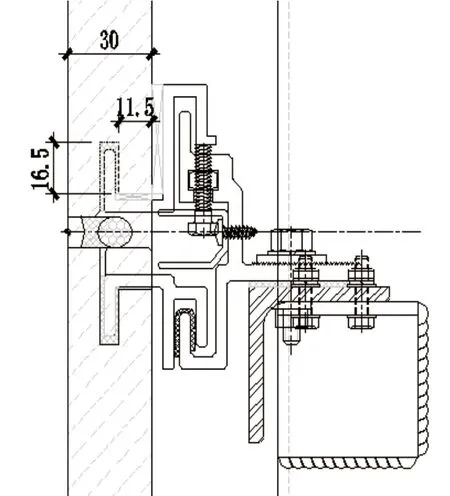
图1 竖剖节点

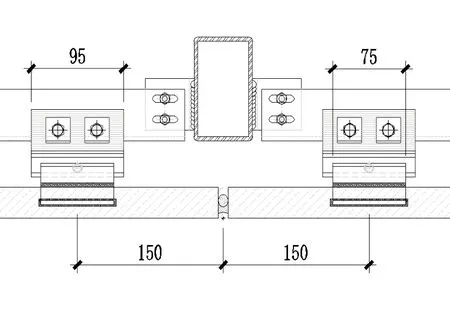
图2 横剖节点

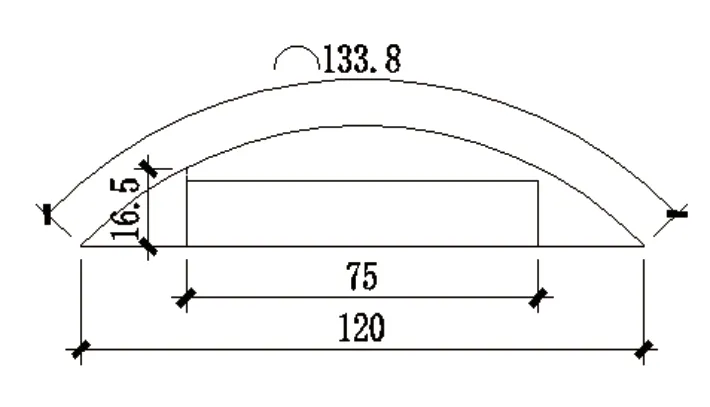
图3 开槽方式

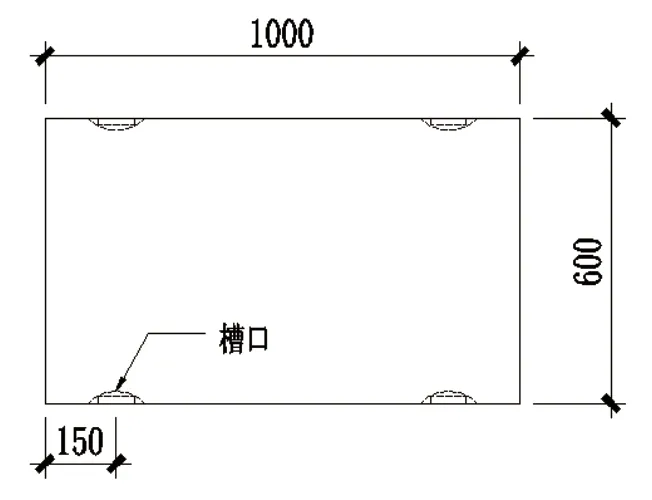
图4 槽口布置

1.1 公式计算

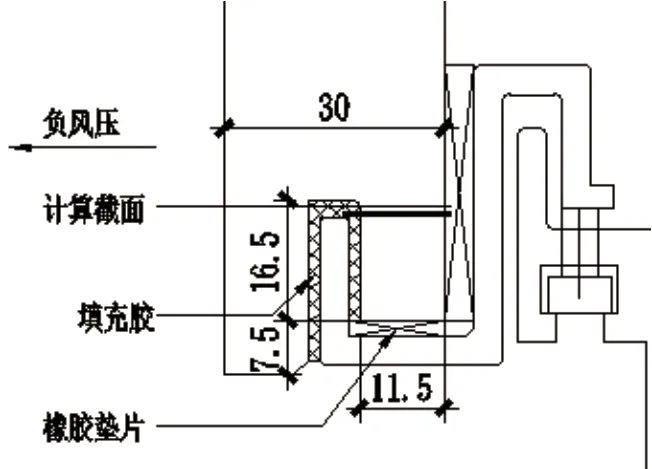
图5 槽口局部尺寸

根据初步定性分析，槽口内侧根部受力最为不利。金属挂件厚度导致槽口内侧受剪面积比外侧小。另外，常规情况下计算负风压大于正风压，负风压通过填充胶传递给槽口内侧石材，并由该计算截面全部承担，而正风压大部分传递给石材背面橡胶垫片与金属挂件，为承压受力方式，而石材的抗压承载力大于100MPa。根据规范计算宽度取总厚度减去开槽宽度，鉴于一般项目现场施工情况，槽口内填充胶体不密实，且AB胶抗拉强度不明确，故本计算只考虑受压侧面槽口有效厚度，即按最不利受力方式取11.5mm，见图5。有限元模型中计算厚度也按照11.5mm，外侧石材与填充胶之间按“Rough”接触类型，接触面之间无拉应力，从而确保负风压在挂件处压力全部传递给内侧石材。

为方便与有限元计算结果对比，应力调整系数β不予以考虑，由于该系数为线性值，计算结果可直接乘上该值而不影响对比结果。

1）槽口截面抗剪计算

风荷载标准值(wk≥1.0kN/m)[2-3]:1.87kN/m2

石材计算厚度t：30mm

30mm厚花岗石重力面密度Gk：0.85kN/m2

水平地震作用标准值qEk=βEαmaxGk[4]：0.353kN/m

水平荷载设计值qh=γωΨωwk+γEΨEqEk：3.06kN/m2

石材分格宽度W：1000mm

石材分格高度H：600mm

石材抗弯承载力设计值fs（MU110等级）：3.7N/mm2

石材抗剪承载力设计值fsv：1.9N/mm2

单个板块挂件数量n：4

槽口计算宽度b：11.5mm

单个槽底总长度s：133.8mm

石材槽口最大剪应力τ[3-4]：

τ==0.30MPa＜1.9MPa

满足抗剪要求。

2）槽口截面抗弯计算

计算截面宽度：133.8mm

计算截面厚度：11.5mm

单个槽口反力设计值：460N

单个槽口弯矩设计值：18860Nmm（集中荷载简化作用于挂件与石材接触面中点）

槽口弯曲正应力设计值：6.39MPa＞3.7MPa

超过石材抗弯强度设计值，需与有限元计算结果进行对比。

1.2 有限元计算

图6 整体模型

石材面板与挂件采用实体建模，采用ANSYS WORKBENCH平台进行模拟。计算模型采用整体模型和局部模型。由于石材重量采用下支撑，受力复杂，故对下部槽口进行全比例建模，充分考虑各部分实际刚度与接触受力，上部槽口采用简化滑动铰接支座。整体模型见图6（石材背面视图），槽口细节见图7。为对比整体模型计算结构的可靠性，还考虑局部模型，对局部采用更小单元网格划分，以直接加载方式进行计算。

规范要求石材槽口内填嵌胶粘剂充盈度应不小于80%[5]，计算模型中胶粘剂不填满，仅考虑挂件与石材正对面空间内填充。胶粘剂弹性模量取2000MPa，压剪强度取标准条件下数值10MPa[6]。橡胶垫片弹性模量取6000MPa。

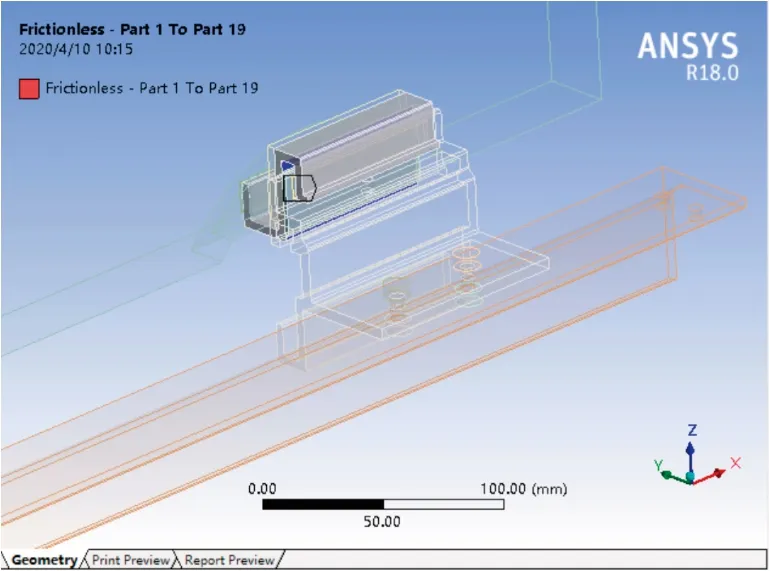
图7 槽口细节

为避免畸变应力影响，各计算截面阴角部位均按R=1mm倒圆角。石材槽口内侧长边界单元划分尺寸7mm，相对短边部位控制在0.7～3mm之间，其他部位单元划分尺寸按照默认设置。槽口外侧胶粘剂为Rough接触，内侧为No Separation接触，胶粘剂、橡胶垫与铝合金之间为Bond接触，铝合金挂件之间、挂件与角钢横梁之间为Frictionless接触，其他根据受力情况简化设置。

角钢横梁两端为铰接支座并约束扭转，上部挂件为铰接支座。水平荷载以均布荷载作用于石材外表面，自重按重力加速度考虑，荷载均为设计值。

石材最大应力发生在槽口部位，最大主应力σ1=6.7642MPa（图8），最大剪应力τ=1.8608MPa（图9）（剖切面显示，向上为石材外表面方向）。

图8 整体模型主应力云图

以整体模型为基础对局部网格细化，单元尺寸控制3mm，石材周边为简支边，局部施加盒子，重点分析局部应力。最大主应力σ1=7.315MPa（图10），最大剪应力τ=1.7419MPa（图11），与整体模型计算结果基本一致，由此可判断有限元计算结果可靠性。最小剪应力-10.454位于石材边缘尖角处，属于应力奇异，非危险部位结果可忽略。

有限元整体模型、局部模型计算结果趋于一致，数值相差6%～8%范围内。公式计算最大剪应力0.30MPa，与有限元整体模型、局部模型计算结果平均值差异较大，有限元结果是公式计算的6.03倍；公式计算最大主应力6.39MPa，与有限元计算结果平均值接近，相差10.2%，两种计算方法主应力超过石材抗弯强度设计值，但均小于花岗石强度标准值最小值8MPa。剪应力与正应力结果均显示该局部应力水平高、分布复杂。

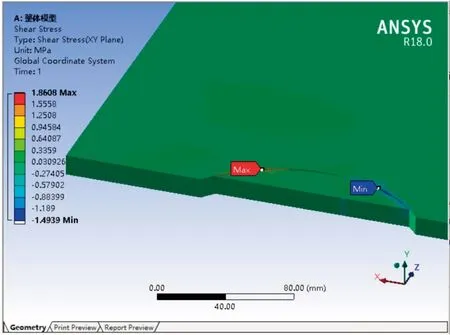
图9 整体模型剪应力云图

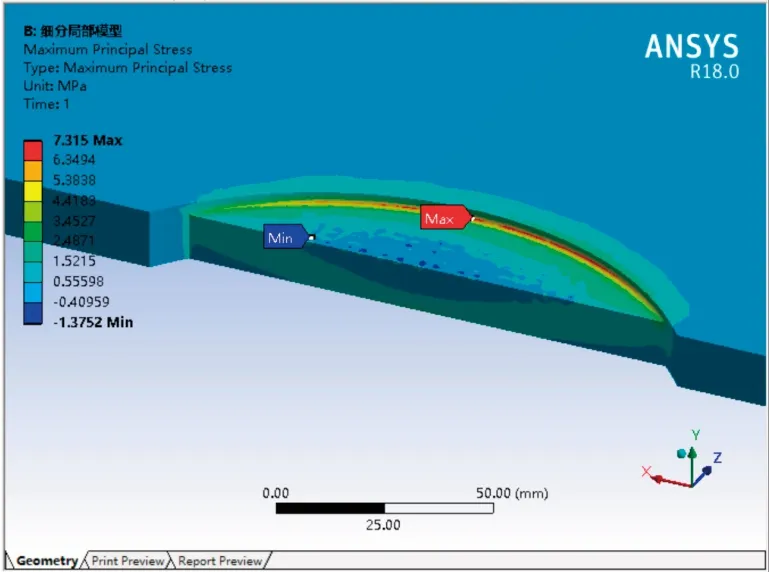
图10 细分模型主应力云图

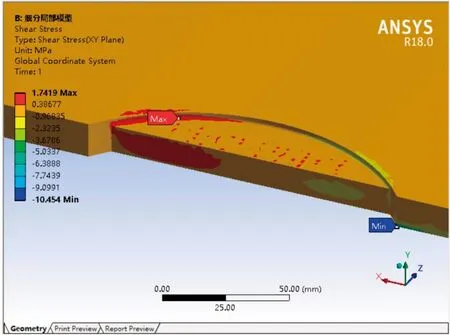
图11 细分模型剪应力云图

1.3 小结

1）公式与有限元结果对比：剪应力差异大，最大主应力比较接近；2）由于槽口抗弯没有相关简化计算方法，且局部应力大，有限元结果提示槽口应力分布复杂，需要深入研究并以试验来验证；3）规范公式考虑槽口内外双层石材共同受力，还有待进一步研究；4）本计算未考虑槽口微损伤，石材自身强度特征值安全系数及质量验收标准来保证。

2 挂件抗弯强度分析

铝合金挂件简化计算中，挂件与角钢之间按固接，力的作用点取最不利位置，即自重作用点取石材面板重心、水平荷载作用点取挂件接触中点，不考虑安装误差。

2.1 公式计算

水平荷载设计值qh：3.06kN/m2

自重均布荷载设计值qg：1.10kN/m2

石材单个槽口受水平力设计值N=qhwh/4：0.46kN/m2

石材单个槽口受竖向力（自重）设计值V=qgwh/2：0.33kN

竖向力偏心L：45mm

水平力偏心e：46.5mm（见图12）

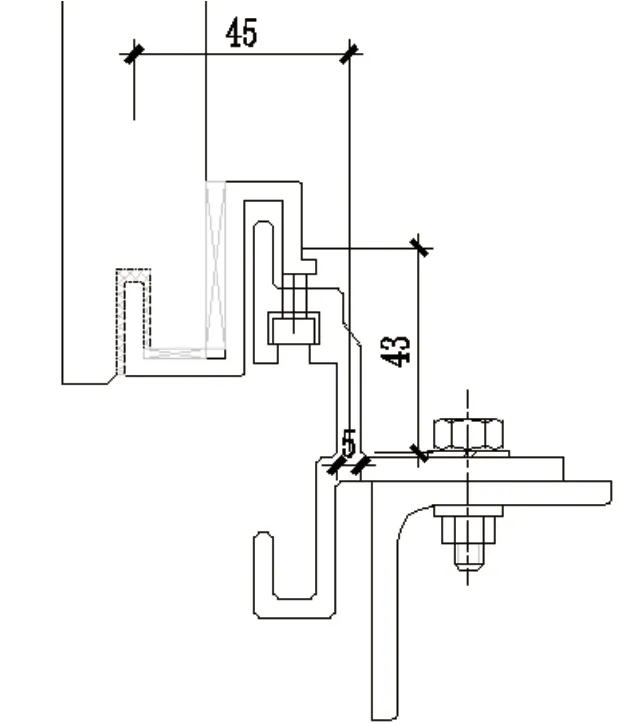
图12 挂件偏心尺寸

弯矩设计值M=VL+Ne：35834.8Nmm

铝合金挂件截面宽度b：95mm

铝合金挂件截面厚度t：5mm

抗弯截面模量W=bt2/6：395.8mm3

铝合金抗弯强度设计值(6063-T6)：150MPa

计算截面正应力设计值σ：

σ=M/W=81.1MPa＜150MPa

铝合金挂件抗弯满足强度要求。

2.2 有限元计算

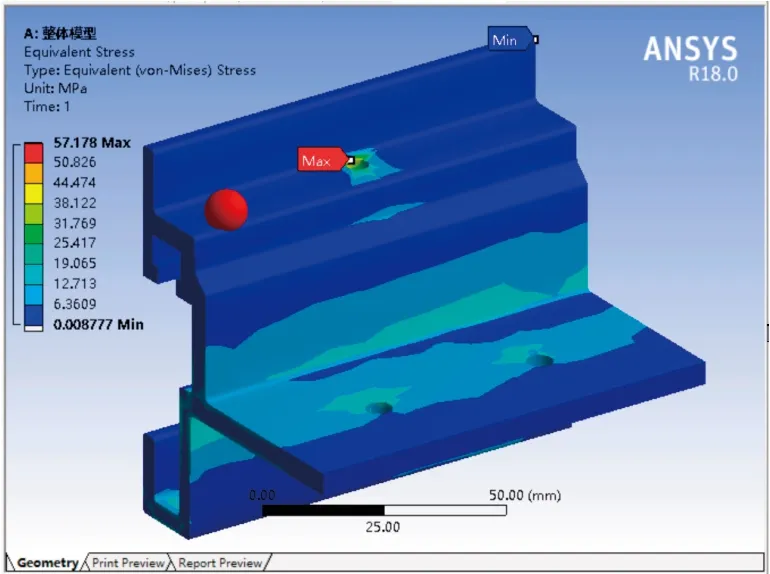
图13 整体模型等效应力云图

计算模型即槽口计算整体模型。铝合金挂件之间为橡胶垫片，垫片一侧为Bond接触，另一侧为Frictionless接触，保证挂件之间为可自由滑动顶紧连接。由于胶粘剂、橡胶垫片弹性模量相对石材、铝合金较小，模型中通过模拟软性材料压缩及接触，充分考虑各个材料之间的接触影响，

整体模型铝合金挂件根部最大等效应力25.417MPa（图13），局部模型根部最大应力26.089MPa（图14）。

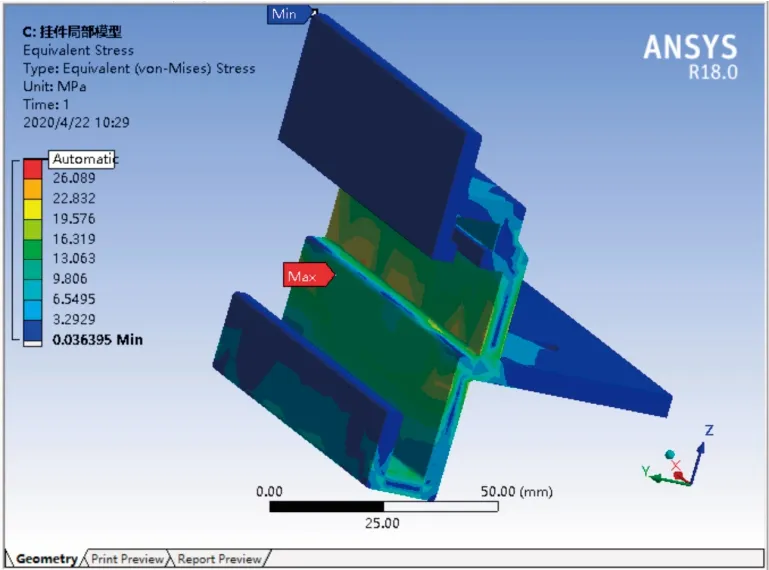
图14 局部模型等效应力云图

2.3 小结

1）公式计算计算结果比有限元计算结果偏大，可能由于简化模型中作用点取最不利值，而有限元计算过程中力矩重分配使得弯矩降低；2）以往幕墙测试结果也验证挂件满足安全要求，故公式计算结果偏于保守，能够保证结构安全。

3 结语

1）通过有限元对比计算，负风压作用下公式计算抗剪强度不够全面且应力偏低，另外石材槽口应力分布复杂，弯曲应力大，在工程设计中需要重点考虑，有待更深入研究，并以试验来验证；

2）金属挂件强度计算按照材料力学公式，取最不利力臂，能够保证结构安全；

3）局部连接强度应同时通过公式计算、有限元对比分析和试验验证，才能充分保证石材幕墙挂件连接安全性。