元指导:基于素养与单元的学习指导范式
李昌官
元指导:基于素养与单元的学习指导范式
李昌官
(浙江省台州市教育教学研究院,浙江 台州 318000)
当下许多学习指导或演变为指令,或只是一招一式的指点,难以达到发展思维、提升素养之目的.应以单元为单位,以发展学生数学学科核心素养为目的,实施具有较强初始性、观念性、框架性、系统性和激励性的学习指导,即“元指导”.“元指导”的主要策略与方法是基于数学学科核心素养的内涵与生成机制,基于数学知识发展的内在逻辑,基于学生的数学认知基础与研究障碍,以数学问题的提出与解决为重点,强化学习的大背景、大问题、大框架、大策略.最后以集合单元为例,具体阐明如何实施“元指导”.
单元教学;元指导;学习指导范式;数学学科核心素养
1 “元指导”提出的背景与缘由
当下,为核心素养而教正在成为越来越多数学教师的共识,但与培育核心素养相适应的学生学习指导范式还远没有建立起来.目前的数学学习指导普遍存在如下四大问题:第一,指导的目的主要是接受教材或教师已有的思维结果,而不是发展思维、提升素养;第二,指导的内容主要是就事论事的、注重细节的方法与技巧,而不是解决一般性问题的普适性、原理性强的策略与方法,也不是思维的缘由与依据;第三,指导的方式主要是单向的、缺乏缘由与依据的指令,而不是对话、交流与暗示;第四,指导的适用对象主要是课时教学与知识点教学,而不是更利于数学学科核心素养生成的单元教学和大概念教学.鉴于教师的主要职责是激励和指导学生学习,并且目前多数学习指导不利于数学学科核心素养的发展,因此应从学生普遍存在的不足——思维的整体性、连贯性、策略性与创新性弱——入手,反思和寻找教师学习指导存在的问题,进而建立与孕育数学学科核心素养相适应的学习指导范式.
2 “元指导”的含义与价值
2.1 “元指导”的含义与特征
2.1.1 “元”的含义
中西方对“元”的含义的理解有较大差异,这反映了中西方不同的文化传统.中国文化背景下的“元”主要有如下5层含义:一是初始的、第一,如,元旦、元月、元年、纪元;二是为首的、居首的,如,元首、元老、元帅、元勋、元凶、状元;三是主要的、根本的,如,元音、元件、元气;四是构成一个整体的,如,单元;五是元素、要素,如,一元论、二元论[1].西方文化背景下的“元”源于英文“meta”,有“……之上、之后”和“超越”等意思.它反映了西方文化形而上、理性至上的传统,意味着一种更高级的逻辑形式.如,“元哲学”“元教育学”“元社会学”“元数学”等各种“元理论”中的“元”.这里的“元”是指中国文化背景下的“元”.它在时间上先于同类事物,在功能上影响和决定同类事物.
2.1.2 “元指导”的含义
“元指导”是指为了有效地帮助学生发现和提出问题、分析和解决问题,促进他们能力和素养的发展,从学习的条件、原理、规律和构成要素出发,对学生的学习与研究进行具有较强观念性、策略性、框架性的指导.它的主要目的是弄清楚学习与研究的目标、思路、策略与框架,而不是具体的方法和细节;它的着力点是揭示学习与研究的大背景、大问题、大框架,明晰与解决大问题相适应的大观念、大思路和大策略.这里的“大背景”是指蕴含着比较大的数学问题的比较大的情境或背景;“大问题”是指时间上先于其它问题,内容上涵盖其它问题,其它问题由它派生出来,或其它问题的解决是为之服务的具有较强本原性、根本性的学科核心问题,亦即对整个单元学习和研究起统率与引领作用的问题.
2.1.3 “元指导”的特征
有研究指出,教对学的指导应突出多样性、必要性、整体性、灵活性和合理性[2].与通常的学习指导相比,“元指导”具有下列特征.
一是初始性.心理学研究表明:预告呈现概念框架和总括地图、提供认知策略有助于学习者较快较深入地学习[3];在学习特定的主题或解决特定的问题之前,缺乏基础性、观念性思维框架指导的学习与探究是盲目的、低效的、不经济的.“元指导”宜在问题提出和解决之初进行,而不宜在研究过程中和研究之后进行.因为只有这样,它才能为后续学习提供观念、框架和策略的支撑.
二是观念性.每个学科(包括各数学分支)都有一些对本学科学习和研究具有广泛、持久、深刻影响的基本数学思想方法和基本思维策略方法,它们共同组成这个学科的学科观念.发展学生的学科观念,既是学科教学的重要目标,也是学生学好本学科的重要途径与方式.“元指导”的观念性主要表现在:(1)它是在信念、策略、原理等方面对学生如何提出问题与解决问题进行指导;(2)它的产生和提出是自然的、合理的,甚至是必然的,它的源头是普通的数学常识而不是什么高深的理论;(3)它着眼于形成、完善和发展解决问题的心智系统,为以后解决同类问题或更具一般性、普遍性的问题做好准备,而不是就事论事地解决眼前问题.
三是框架性.波利亚曾指出:“如果你深入到细节中去,你就可能在细节中迷失自我.过多过细的枝节对思维是一种负担.它们会阻碍你对要点投入足够的注意力,甚至会使你全然看不到要点.”[4]“元指导”的框架性是指为了解决大问题,建立一种具有较强结构性、整体性的解决问题的思路与框架.也就是说,“元指导”不针对局部或细节的问题,也不探讨具体的、细枝末节的技能与技巧,它的目的是形成初步的、框架性解决问题的方案.
四是系统性.“元指导”的系统性有如下3层含义.(1)将待解决的问题作为一个整体、一个系统来看待和处理;(2)从宏观上、整体上进行指导,形成一个系统的、连贯的、逻辑一致、前后呼应并相互支持的指导体系,因为思维应是“一个持续的、有步骤的过程;前一步决定后一步的结果,后一步参照前一步的成因;一步一步,相因而发生,相辅而成立……相互连贯,持续地向着一个共同的目标前进”[5];(3)这种系统性、连贯性是通过揭示数学知识内在的结构、联系来实现的,因为思维的中心因素是“一种事物指示或预示另外一种事物”[6].
五是激励性.“所有图式,不管它是什么,都同时是情感的和认知的”[7];智力只提供方法与技术,而情感则为行为指定目标、提供能量[8].“元指导”的激励性主要表现在如下4个方面.(1)氛围激励,即让学生在良好的氛围中,以愉悦的心情学习与探究;(2)问题激励,让学生在好奇心、好胜心的驱动下,带着问题学习与探究;(3)价值激励,即明确眼前学习与后继学习的关系,以及知识在生活中可能的应用;(4)信念引领,即通过彰显数学的美和逻辑力量激励学生.
六是发展性.智育的本质是智力发展与思维习惯、思维品质的优化;教育的本质是面向未来的.“元指导”不仅关注学生能否解决眼前面临的问题,也关注他们今后能否解决同类问题和相关问题;不仅期待学生能在教师的指导下解决问题,也期待他们今后能够独立地解决问题.
2.2 “元指导”的功能与价值
2.2.1 能满足大概念教学和单元教学的需要
大概念教学、单元教学的特点是“大”;而通常学习指导的特点是“小”,即注重局部、细节,重在解决眼前面临的问题.大概念教学、单元教学的价值取向是更好地发展学生的能力,提升他们的核心素养;而通常学习指导的价值取向则是更好地传授知识和训练技能,提高学生的考试成绩.“元指导”的特点决定了它重本源、重根本、重“四大”(即大背景、大问题、大框架、大策略),因此它能满足大概念教学和单元教学的需要.
2.2.2 为高认知挑战和深度学习搭建平台
尽管理论上大家都认可“自主探究式”学习是发展学生核心素养的有效途径与方式,但实际情况往往是“自主探究式”学习既没有发展学生的思维能力,也不利于“四基”的落实.究其原因,主要是因为学生没有掌握相应的普适性强的认知策略与方法,而教师也没有为学生的探究提供强有力的认知策略支持.因此有效的“自主探究式”学习既需要填平学生独立探究问题所需要的能力与他们实际能力之间的鸿沟,又不能使教师的教沦落为灌输.“元指导”就是具有这种功能的教,它为学生的高认知挑战和深度学习搭建了有效的载体与平台.
2.2.3 有利于提升学生的数学学科核心素养
核心素养的内核是价值、精神与观念;核心素养的主体是人的思考力与学习力,是主动学习、主动探究的意识与能力.核心素养离不开知识,但知识未必能转化为素养.“元指导”把数学知识作为学生自主探究和建构的对象,从思维的原理与方法出发对学生的探究进行带根本性、原理性的指导,着力教给学生“结构更好、层次更高、价值更大的知识”[9],有利于学生在有意义的学习过程中获得有意义的结果,有利于学生知识、技能、思维、品性的协调发展和综合发展,有利于学生所学的知识与技能更好地转化为能力与素养.
3 “元指导”的依据与策略
许多学者从不同视角对数学学习指导进行了深入的研究.有学者指出,应利用数学是常识的精微化指导数学教与学[10];也有学者提出,应利用数学方法论[11-12]、认知弹性理论[13]指导数学教与学.“元指导”的实质是从情感与认知两方面为学生的探究提供先行组织者.它通过明确学习的目标与价值来促进学生形成学习的心理倾向,通过提供认知策略、概念框架和心理地图提升学生的认知能力.
3.1 数学学科核心素养的内涵与生成机制
教学目标影响甚至决定着教学方法与学习方法;反之,教学方法与学习方法也影响甚至决定着教学目标的落实,决定着学生学到知识的类别与认知维度.“元指导”应围绕核心素养,为更好地培育、提升学生核心素养展开;应基于数学学科核心素养的内涵与孕育机制展开.实施“元指导”时,应既有各学科共同的目标——中国学生发展核心素养意识,也有数学学科核心素养意识;应在充分认识和把握数学教学目标的整体性与层次性的基础上,处理好数学知识、技能、思想方法与核心素养的关系,既注重“四基”“四能”的落实,又有意识地对“四基”“四能”进行提炼和升华,使之更好地积淀为包含理性思维、批判质疑、勇于探究等在内的科学精神[14];应更多地关注思维的缘由、依据、过程与方法,而不仅仅是思维的结果;应让学生更多地在更高水平上参与问题体系的建构和问题解决策略的探讨,因为素养只能在亲身实践、用心感悟的过程中形成与发展.
3.2 数学知识发展的内在逻辑
每门学科的发展都有其内在的逻辑.数学及其各分支的发展通常都遵循“大三步曲”——源于生活、高于生活、服务于生活.数学发展的基本途径与方式是舍弃物质的一切非数学属性,从数与形两方面对现实世界进行归纳、抽象、建模,是借助直观想象、逻辑推理、数学运算思考和解决问题.数学先是通过抽象化、理想化、符号化把现实世界的问题转化为数学问题、数学模型,再通过公理化、结构化、形式化对数学材料进行组织、整理和拓展,建构特定的数学知识体系[15].数学学科中,解决问题的基本思维方法是建立概念,明晰概念与概念之间的联系——定理,再从概念、定理出发,进行运算或推理.数学概念的建立、数学定理的确认都有其内在的标准与要求.数学不仅建构了具有统一性、简约性、结构性与和谐性的知识大厦,而且还提供了能够有效地解决各种现实问题的数学技术与工具,形成了“逢山开路、遇水架桥”、追根溯源、严谨求实、崇尚理性的数学文化与数学精神.
3.3 学生的数学认知基础与研究障碍
由于“学习在很大程度上依赖于个体和与之发生相互作用的环境事件”[16],并且“每一种新的性能的学习都有不同的先前学习的起点并且很可能也要求不同的外部情境”,教学“首先必须注意存在于学习者内部的性能,其次要注意学习者外部的刺激情境”[16].因此“元指导”应帮助学生在数学问题的提出和解决与他们认知结构中已有的相关观念、相关经验之间建立起清晰的、实质性的联系,以便更好地克服研究的困难与障碍.也就是说,只有基于学生的认知基础、认知潜能,搞清楚哪些问题学生能够自主解决,哪些问题学生可能会遇到障碍,以及为克服这些障碍需要教师指导什么、指导到何种程度,“元指导”才能取得好的效果.
3.4 以数学问题的提出和解决为重点
数学的核心是问题与解,“为全体学生的中小学数学,其核心应放在人类数学问题的提出和解决上”[17],因此数学学习的核心是如何从数学角度发现和提出问题、分析和解决问题.这既是数学课程的重要目标,也是提高学生“四能”的重要途径与方式,是发展学生数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等数学学科核心素养的重要手段.鉴于发现和提出数学问题具有十分重要的教育价值,并且学生在这方面的意识与能力又十分薄弱,因此数学教学应加强发现和提出问题策略的指导.鉴于学生自主建构数学概念、发现数学定理法则、解决数学产生与发展所依赖的问题的能力也十分薄弱,并且数学教学又不能降格为灌输和机械模仿,因此数学教学应加强学生自主建构知识和解决问题策略的指导.由于抓住了数学问题及其解决策略的指导,就抓住了数学教学的核心与关键,因此“元指导”的重点应放在数学问题的提出与解决上,放在数学问题提出与解决的原则、策略与方法上.应通过“元指导”,帮助学生形成以大问题为核心、具有思维导图与研究的技术路线图性质的数学问题体系,形成既能解决当前问题又具有较强迁移功能的解决问题的策略与方法体系.
3.5 强化学习与研究的“四大”
“元指导”尤其适宜于单元起始教学,它与通常的学习指导有明显的区别.这种区别主要表现在:第一,“元指导”突出和强化“四大”,即大背景、大问题、大框架、大策略,它更加重视从宏观上、整体上为解决一般问题提供普适性强的思路与策略,更加重视学科的一般观念与解决问题的基本思路;第二,“元指导”要求形成“心智引领”(即统领性、原理性强的解决问题的思路)、“支架引领”(即整体性、结构性强的解决问题的具体方案)、“技术引领”(即突破难点的技术与方法)三位一体,完整的、层次分明的指导体系;第三,“元指导”反对就知识论知识、就技能论技能,它要求揭示数学知识、数学技能背后所蕴含的数学思维与问题解决策略,它追求的是知识、技能、思维、策略、情感等要素的相互融合与相互促进[9].
4 一个案例——集合单元的“元指导”
4.1 集合单元“元指导”的基础与依据
4.1.1 知识发展的内在逻辑
集合是高中数学的起始课,集合语言是现代数学的基本语言,集合思想是现代数学的基本思想方法.集合概念不仅是刻画具有“类”特征的研究对象的需要,更是从数学视角对它们进行简捷、准确处理的需要,即运算的需要.集合单元面临的主要问题有两个:一是如何用准确无误的数学概念来界定数学研究对象的范围;二是如何建立关于这些研究对象的运算及其运算法则.由于准确无误的运算需要建立在严谨的、清晰的、毫无歧义的概念的基础上,因此集合概念、集合间的关系、集合运算是一个前后一致、逻辑连贯的整体.集合概念是集合运算的基础,同时也正是集合运算的需要,决定了集合元素应具有确定性、互异性与无序性.构建集合概念只解决了如何刻画作为研究对象的“类”的问题,是集合研究的第一步;研究集合间的关系既是深化对集合认识的需要,也是为集合运算铺平道路的需要,是集合研究的第二步;研究集合的第三步亦即其深层次目的,是要建立集合运算,进而使集合作为思想与工具具有更大的威力与价值.
4.1.2 学生认知基础与研究障碍
数学知识、数学经验方面,学生已经在小学、初中接触过整数集、解集、有理数集等,也有“物以类聚,人以群分”的生活经验,但他们对集合概念及其表示法等缺乏清晰的、系统的认识;他们有数的大小比较、数的运算方面的经验,但由于集合与数存在较大的差异,他们往往难以类比和迁移.思维策略与数学能力方面,学生解决现成的、有固定模式的数学习题能力较强,而建构数学概念、发现数学定理方面的能力非常薄弱.学习习惯、学习方式方面,学生习惯于接受现成的、成熟的知识,而不习惯于自主探究、自我建构知识.
集合单元学习,学生会遇到如下4个难点.一是集合概念的建构,因为学生往往不理解集合概念的产生背景与目标指向,并且他们也缺乏建构类似概念的经验;二是集合表示方法的探索与建构,因为学生不会自觉地根据严谨、简洁、准确的原则探索集合的表示方法,并且他们往往从形式上而非本质上理解集合的表示方法;三是集合思想的形成与集合语言的运用,因为它们不仅与学生原来的思维习惯和语言习惯有较大的差异,而且都需要较长时间的实践才能真正形成和发展;四是类比数的运算,建立集合的基本运算法则,并据此进行相关运算.
4.1.3 核心素养的生成机制
集合单元教学,如果学生以“听讲接受”的方式获取知识,那么他们将失去一个发展数学学科核心素养的机会;如果学生以“自主探究”的方式获取知识,那么他们将面临自身认知基础与能力的不足,实际效果也将不如人意.因此基于发展核心素养的需要,对学生进行“元指导”是解决“听讲接受”与“自主探究”矛盾的最好途径与方式.
为了更好地促进核心素养的生成,数学探究应是在明确的数学问题驱动下,在明确的思维策略引导下的理性的、有条理的、合乎逻辑的思考与探究,而不是小白鼠走迷宫式的偶然发现,不是“摸着石头过河”和“瞎子摸象”式的探究.就单元教学而言,这种探究不应一开始就陷入局部的细节问题,而应先探索解决问题的总体思路与框架.相应地,基于单元、指向核心素养的“元指导”应建构学习与探究的技术路线图,促进学生自主、有效地建构数学知识,促进他们知识、技能、思维与品性的协调发展;应尽可能在学生学习本单元内容之初进行,以便为后续学习提供先行组织者.如果难以一次性完成,或学生一时无法理解与消化,也可安排部分“元指导”在学习过程中进行.需要注意的是,“元指导”并不是教师的“独角戏”,应尽可能多地让学生参与讨论与建构.
4.1.4 集合单元的学习目标
根据学习内容的特点及其所蕴含的教育价值,基于学生的认知基础与认知潜能,制定集合单元的学习目标如下.
(1)通过实例,理解集合的含义,理解集合与元素的关系、集合元素的特征;理解集合之间包含与相等的含义,能识别给定集合的子集、真子集;理解并集、交集、补集的含义,能求两个集合的并集、交集和给定全集的子集的补集.
(2)能体会、感受和欣赏集合语言的简洁性与准确性,能分别用自然语言、图形语言和符号语言刻画集合,表达集合的基本关系与基本运算.
(3)经历发现和提出、分析与解决相关数学问题的过程,能感受和体会集合概念、集合基本关系、集合基本运算的建构思路与方法,能感受和体会集合知识形成与发展过程中所蕴含的数学抽象、直观想象、数学建模、逻辑推理、数学运算等思想与方法.
4.2 集合单元“元指导”的步骤与方法
4.2.1 揭示大背景 提出大问题
鉴于任何问题的产生都有其背景、缘由与目标指向,并且明确这些对学生理解知识的来龙去脉、学会发现与提出问题具有重要的意义,因此“元指导”应揭示数学问题产生的背景与缘由.
学生学习集合的大背景是数学的学科特点与功能——“数学是刻画现实世界的语言与工具,是运算和推理、表达和交流的语言与工具”;“物以类聚,人以群分”是一种常见的自然和社会现象,人们往往需要以“类”为单位对事物进行研究,搞清楚同“类”事物的共同属性,“类”与“类”之间的关系,以及“类”与“类”之间的运算.根据这个大背景,提出如下大问题:如何从数学角度刻画某些具有“类”特征的研究对象,进而明确它们之间的关系,建立它们之间的运算?
4.2.2 建立大框架 明确大思路
天下大事作于细,天下难事作于易.解决大问题,需要把它分解为一系列“子问题”“孙问题”,建立相应的大框架,明确相应的大思路.“元指导”尽最大可能建构清晰完整的、以大问题为核心的问题体系,形成解决大问题的大框架与大思路(见表1).
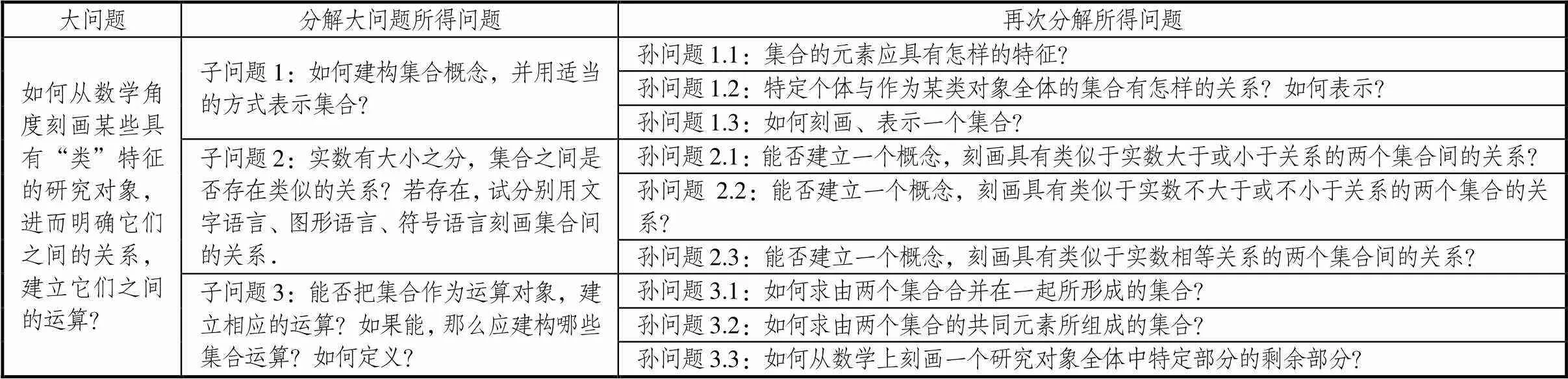
表1 解决集合单元大问题的大框架与大思路
建立大框架、明确大思路时,需要注意如下几点.第一,尽可能多地让学生参与讨论和建立,尽可能让学生明白每一个问题提出的背景与缘由.如,子问题1提出的背景与缘由是数学是基于概念的,数学概念是数学思维的出发点,界定概念、表征概念是数学研究的基础;子问题2提出的背景与缘由是数学是研究关系的科学,搞清楚集合与集合之间的关系是建立集合运算的前提和基础;子问题3提出的背景与缘由是数学是关于算子与算法的科学,运算是数学的威力之所在,通过运算高效、便捷地处理研究对象是数学研究问题的基本方式,建立集合运算法则,研究集合运算律是集合知识发展的逻辑必然.第二,问题的价值在于引发学生思考、促进学生学习,因此不必过于在意学生能否解决这些问题,尤其不能要求或希望学生在单元起始课就能解决.有些问题可由教师自问自答,有些问题可让学生合作讨论,有些问题可只解决其中部分环节.第三,根据学习与研究的需要,可对分解所得子问题继续进行分解,尽可能形成清晰的、层次分明的问题体系.
4.2.3 形成大策略 寻求大方法
如果说建立解决问题的大框架应重在遵循数学知识发展的内在逻辑,那么形成解决大策略应重在遵循学生思维发展的内在规律.
策略方法1:归纳、抽象、建模.归纳、抽象、建模是建构数学概念、发现数学定理法则最常用的思维策略与思维方法.集合单元教学中,无论是集合的概念、表示法,还是集合间的基本关系与基本运算,都应通过归纳、抽象、建模得到.教师应让学生亲身经历完整的抽象与建模的过程——感知与识别、分类与概括、想象与建构、定义与表征、系统化与结构化,不断丰富他们的归纳、抽象、建模经验,提高他们的归纳、抽象、建模能力[15].
策略方法2:回归现实,寻求启示.数学源于现实,高于现实;数学定理法则与客观现实具有高度的一致性.回归现实,从现实中寻找启发、启示是解决数学问题的基本策略与方法之一.集合单元教学,不仅应通过考察现实世界中的具体研究对象建构集合概念,而且还应该通过回归现实、考察现实世界中研究对象的基本关系和“基本运算”来探索、建构集合的基本关系和基本运算.
策略方法3:类比实数大小关系和实数运算.任何问题的解决总是或多或少地基于原有的相关经验,基于待解决问题与已解决问题之间的相似性,因此应寻找已有的相关经验,寻找与待解决问题具有相似性的已经解决的问题.类比是一个伟大的引路人.研究集合的基本关系与基本运算宜类比实数.因为“实数系是一切具有运算的体系的标兵,让任意运算的对象和数类比,让任意对象的运算和数的运算对比,不仅能使我们获得需要的研究问题,而且能使我们产生研究方法的灵感”[18].
策略方法4:从概念和定理出发思考问题.数学概念是清晰的、准确的,数学定理是严谨的、毫无疑义的.数学大厦是基于概念和定理建构的,数学概念和定理是数学思维的出发点.从概念和定理出发思考问题是常用的数学思维策略与方法.因此应基于集合概念探索集合的表示方法、基本关系、基本运算,应基于集合的基本关系探索集合的基本运算.
策略方法5:寻找集合关系与集合运算的几何直观.由于数学大厦是通过舍弃物质的一切非数学属性,从数与形两方面对现实世界进行抽象建构的,因此从数与形两方面入手是分析数学问题、解决数学问题的基本策略与方法.由于“图形不仅是几何题目的对象,而且对任何一开始跟几何没有关系的题目,图形也是一个重要的帮手”[4],因此应“把遇到的数量关系设法用几何图形表示出来”[18].就集合单元教学而言,不仅应充分利用韦恩图来形象地说明集合的基本关系与基本运算,而且还应注意图形语言、文字语言与符号语言之间的相互转换.
5 结束语
“元指导”是一个新的有待深入研究的课题.应加强对“元指导”的研究,开展对学习指导的指导,使“元指导”更好地服务于数学课程改革和教学改革,更好地促进学生数学学科核心素养的发展.
[1] 辞海编辑委员会.辞海(第六版缩印本)[M].上海:上海辞书出版社,2010:2 337.
[2] 罗萍萍.教学指导方式多样化策略的实证研究[J].数学教育学报,2012,21(4):48–51.
[3] E·詹森.基于脑的学习[M].梁平,译.上海:华东师范大学出版社,2008:69–73.
[4] G·波利亚.怎样解题[M].涂泓,冯承天,译.上海:上海科技教育出版社,2002:77,105.
[5] 约翰·杜威.思维的本质[M].孟宪承,俞庆棠,译.北京:台海出版社,2018:4–5.
[6] 约翰·杜威.我们怎样思维 经验与教育[M].伍中友,译.北京:人民教育出版社,2005:17.
[7] 克努兹·伊列雷斯.我们如何学习[M].孙玖璐,译.北京:教育科学出版社,2010:83.
[8] 皮亚杰.智力心理学[M].严和来,姜余,译.北京:商务印书馆,2016:23.
[9] 李昌官.布卢姆认知目标新分类指导下的数学教学设计[J].数学教育学报,2012,21(3):67–71.
[10] 宁连华,涂荣豹.利用数学是常识的精微化指导数学教与学[J].数学教育学报,2001,10(1):25–27.
[11] 张玉峰,芮文娟,周圣武.用数学方法论指导大学数学教学[J].数学教育学报,2014,23(5):76–78.
[12] 常瑞玲.用数学方法论指导极限概念教学的尝试[J].数学教育学报,2000,9(1):78–80.
[13] 李明振,庞坤,宋乃庆.认知弹性理论指导下的高师数学建模教学[J].数学教育学报,2007,16(1):96–99.
[14] 核心素养研究课题组.中国学生发展核心素养[J].中国教育学刊,2016(10):1–3.
[15] 李昌官.数学抽象及其教学[J].数学教育学报,2017,26(4):61–64.
[16] R·M·加涅.学习的条件与教学论[M].皮连生,王映学,郑葳,等译.上海:华东师范大学出版社,1999:2,20.
[17] ERNEST P.数学教育哲学[M].齐建华,张松枝,译.上海:上海教育出版社,1998:335.
[18] 人民教育出版社.普通高中课程标准实验教科书·数学必修1教师教学用书[M].北京:人民教育出版社,2004:4.
Metacognitive Instruction: A Learning Instruction Model Based on Literacies and Learning Units
LI Chang-guan
(Taizhou Institute of Education and Instruction, Zhejiang Taizhou 318000, China)
Nowadays, most learning instructions are either rigid instructions or point-by-point teaching, which have limitations in fulfilling the goals of improving students’ thinking and literacy in mathematics. To achieve the teaching goals in curriculum standards, teachers should instruct students with primary ideas, systematic approaches, and positive incentives, which are termed metacognitive instructions, to develop students’ mathematical literacies through “Curriculum Content Unit” as a basic unit. The approaches and strategies of metacognitive instructions are developed based on the connotations and formation mechanism of mathematical literacies, the inner logic of the development of mathematics, and students’ cognition and obstacles. Metacognitive instruction focuses on students’ problem posing and solving and their learning background, big ideas, big framework, and big strategies they use. Finally, we show a way of using metacognitive instruction to teach students by the unit of “set.”
unit-based teaching; metacognitive instruction; instruction model; mathematical literacies
G40–032
A
1004–9894(2020)05–0064–05
李昌官.元指导:基于素养与单元的学习指导范式[J].数学教育学报,2020,29(5):64-68.
2020–04–10
浙江省教研课题——高中数学研究型教学实践与探索(10455)
李昌官(1964—),男,浙江临海人,正高级教师,特级教师,博士,教育部国培专家,主要从事中学数学课程与教学研究.
[责任编校:周学智、张楠]

