混凝土填充率对STS管幕结构抗弯性能的影响研究
肖俊航,张月君
(1.中国铁路设计集团有限公司,天津 300000; 2.中南建筑设计院, 湖北 武汉 430000)
随着城市化的推进,城市地表基础设施建设逐渐趋于饱和,使得城市道路交通的发展空间受到限制,因此,发展城市地铁工程势在必行[1-2]。以洞桩法为代表的浅埋暗挖地铁车站的施工方法对周围环境影响影响较大[3],而管幕工法作为一种新兴暗挖方法因其环境影响小、施工简单、结构安全可靠和工期短等优点,广泛应用于地铁工程建设领域[4-5]。传统管幕工法因在施工过程中对周围扰动相对较小,在我国一些重点工程进行了运用[6-7]。它是在土体内顶入若干根钢管,通过管间连接实现小断面构建大断面地下结构的施工方法。由于传统管幕结构相邻管间仅用锁扣进行连接,导致其整体管幕结构的抗弯承载力和抵抗变形能力较弱,在开挖管幕下方土体时需要架设大量的临时支撑,给施工带来了不便。基于此,Jia等[8-9]学者提出了一种新型的管幕工法:STS管幕工法,它的相邻管间采用混凝土、螺栓以及翼缘板进行连接进而组成的帷幕支护结构,不仅加强了整体的支护能力,并在必要时提供止水功能。赵文等[10]和贾鹏蛟等[11-13]通过室内试验和数值模拟,研究了STS管幕结构的破坏模式、裂缝开展和受力机制,并系统性的分析了管间连接参数对其抗弯性能的影响。谢欣[14]采用数值模拟方法,在现有规范条件下分析得到STS新型管幕结构抗弯刚度及正截面抗弯承载力的计算公式。赵文等[15]分析了STS管幕结构支护下的土体开挖过程,探讨了不同的开挖台阶尺寸和施工步序等因素对地表沉降及开挖面稳定性的影响。张超哲等[16]采用弹簧模拟STS管幕结构和土体相互作用,探究了原模型和其简化模型的结构受力和整体变形规律。
综上所述,当前学者主要致力于STS管幕结构的破坏机制和连接参数方面的研究,而混凝土在STS管幕结构的密实程度尚未被系统研究。在实际施工过程中,由于具体施工条件的限制,STS管幕结构的管内和管间混凝土存在不密实情况,加之混凝土作为STS管幕结构的重要组成部分,管内外混凝土的密实度对STS管幕结构的受力较为重要。基于此,本文以室内试验为依托,采用有限元软件ABAQUS建立有限元模型,对不同混凝土填充率情况下STS管幕结构抗弯性能进行深入研究。
1 STS管幕结构工作机理简介
STS(Steel Tube Slab,STS)管幕结构是以翼缘板和高强螺栓为横向连接的钢管组,其节点详图如图1所示。该管幕结构与传统管幕最大的区别在于拥有较强的横向承载能力,这使得STS管幕结构能够发挥类似于结构板一样的作用。
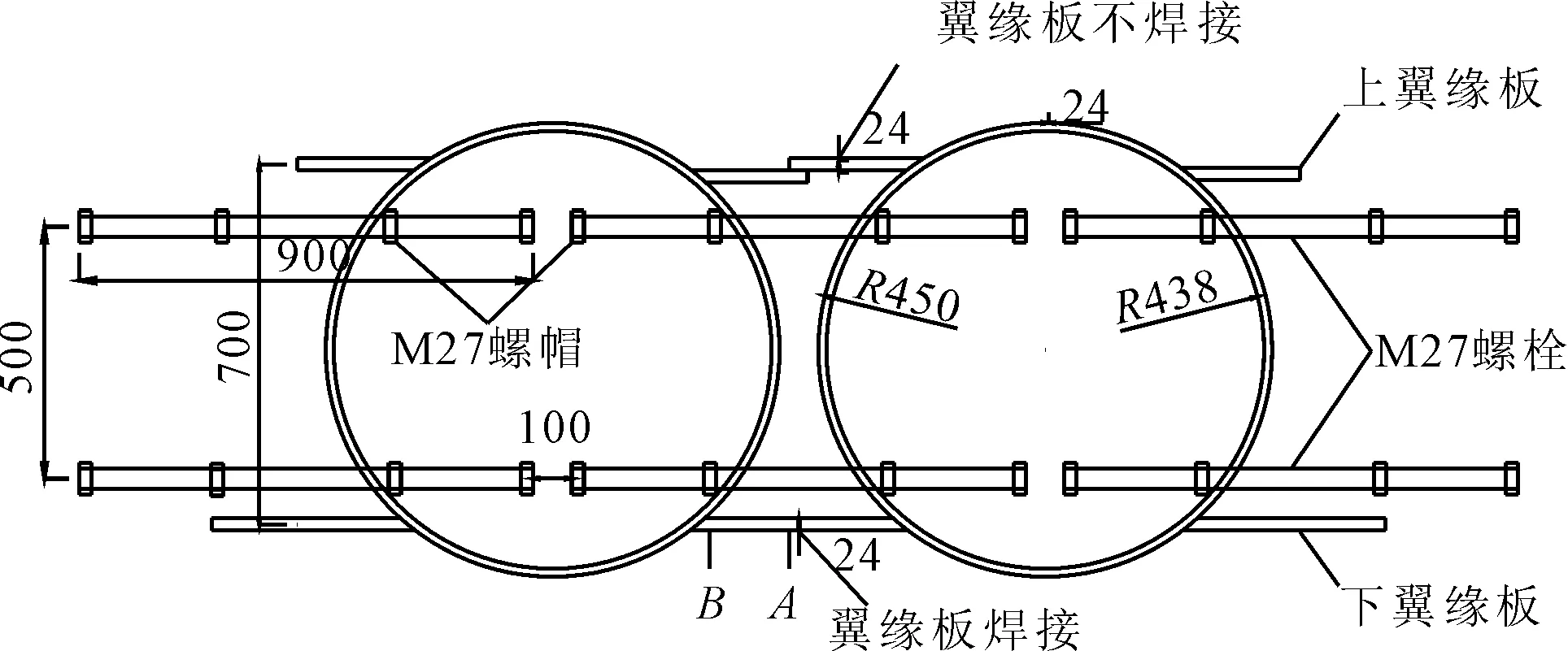
图1 钢管横向连接节点详图(单位:mm)
强效的横向连接改变了STS管幕结构的受力形态,使其作用机理也与传统管幕结构完全不同。当隧道开挖时,因STS管幕结构能够以板状形式承载,充分发挥其横向承载能力,因此可以大大减少内部临时支撑的数量,甚至条件允许的情况下可以不设任何支撑。当不设或少设支撑时,STS管幕结构在沿隧道方向的长度远远超出隧道横断面尺寸的3倍。参照《混凝土结构设计规范》[17](GB 50010—2010)9.1.1条:当长边与短边之比不小于3.0时,宜按沿短边方向受力的单向板计算。此时结构板的受力可以按照平面应变问题简化为梁模型进行计算[18]。STS管幕结构分析单元的选取如图2所示。

图2 STS管幕结构计算单元选取
2 计算模型介绍
2.1 本构模型选取
材料的本构其实质即为应力-应变关系,属于材料内部微观机理的宏观表现。鉴于管内混凝土受外环钢管的约束作用,本文特选用韩林海提出的本构模型参与分析[14]。管间混凝土受压本构模型选取《混凝土结构设计规范》[17](GB 50010—2010)混凝土单轴受压应力-应变关系曲线,如图3所示。螺栓和翼缘板采用双阶段曲线模型来模拟。
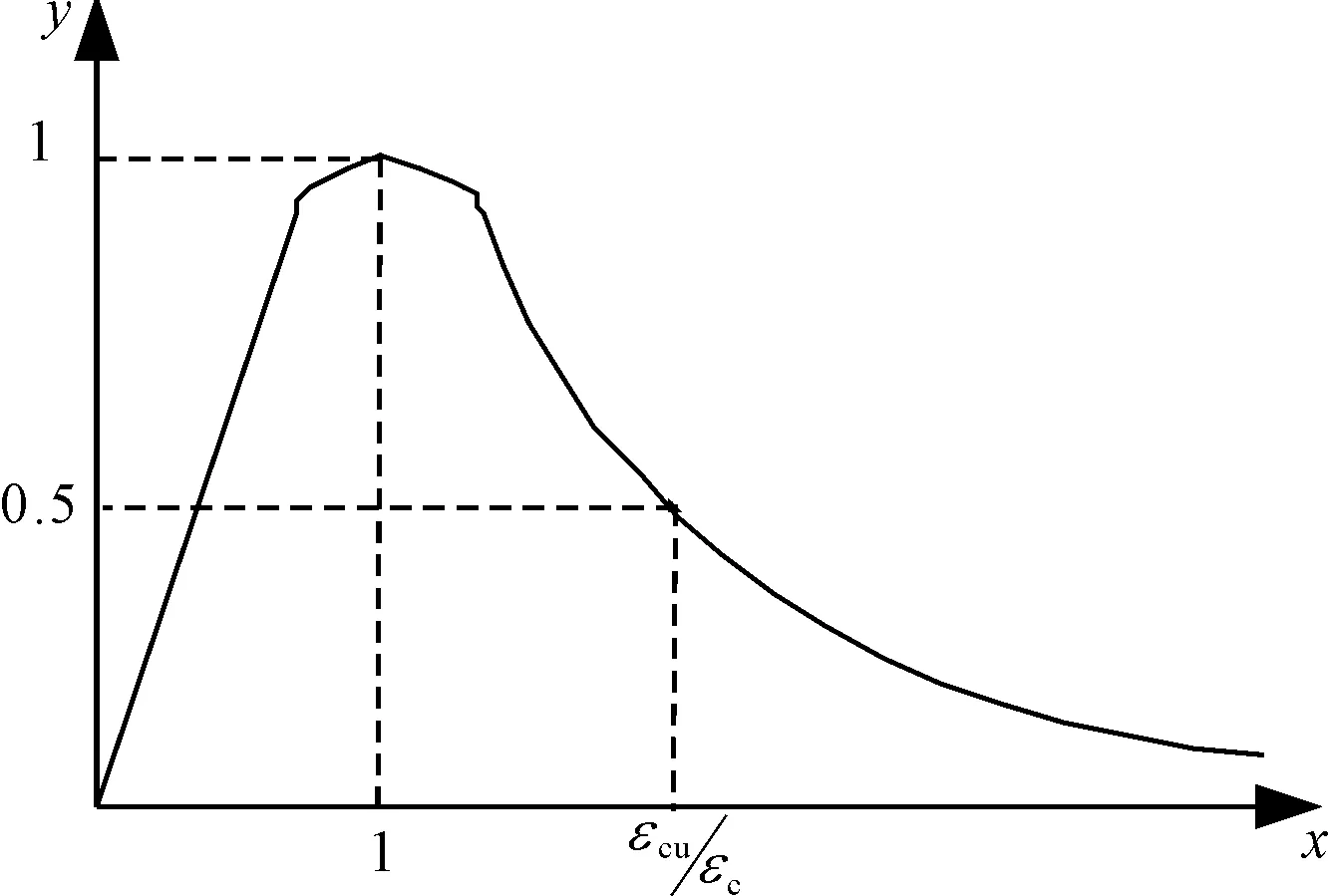
图3 混凝土单轴受压应力与应变关系曲线
2.2 模型参数标定
东北大学各科研工作者做了多组室内模型试验[10,15],本文以文献[10,15]中1∶1试验数据为参照,如图4所示,用ABAQUS软件来模拟相同试验条件下STS管幕结构的力学响应,对比室内试验与数值模拟试验结果,以验证各部件选取的本构模型的合理性。管内以及管间填充材料选用C30混凝土,钢管以及翼缘板选用Q235B工字钢,横向螺栓选用8.8级高强螺栓。模型取1m宽度,采用单点集中力加载模式,其中钢管细部尺寸如表1所示,模型尺寸图如图1所示。

图4 STS管幕结构1∶1试验图

表1 STS管幕结构对比组细部尺寸
模型中分别包含钢管、翼缘板、管内混凝土、管间混凝土、横向螺栓以及支座垫板共六个细部结构。钢管与翼缘板采用四节点减缩积分格式的壳单元(S4R);混凝土和垫板采用八节点减缩积分格式的三维实体单元(C3D8R);螺栓采用两节点线性积分格式的三维桁架单元(T3D2)。垫板与STS管幕结构通过Tie约束连接,在加载垫板上方建立参考点,并且将该参考点与垫板Couping起来,用以施加集中荷载;螺栓与整体结构之间采用Embedded约束,在钢管、翼缘板与混凝土之间建立面-面接触(Surface to Surface),以“罚函数”定义接触面的切向特性,摩擦因数取0.3,以“硬接触”定义接触面的法向特性。两个对比组的整体模型如图5所示。
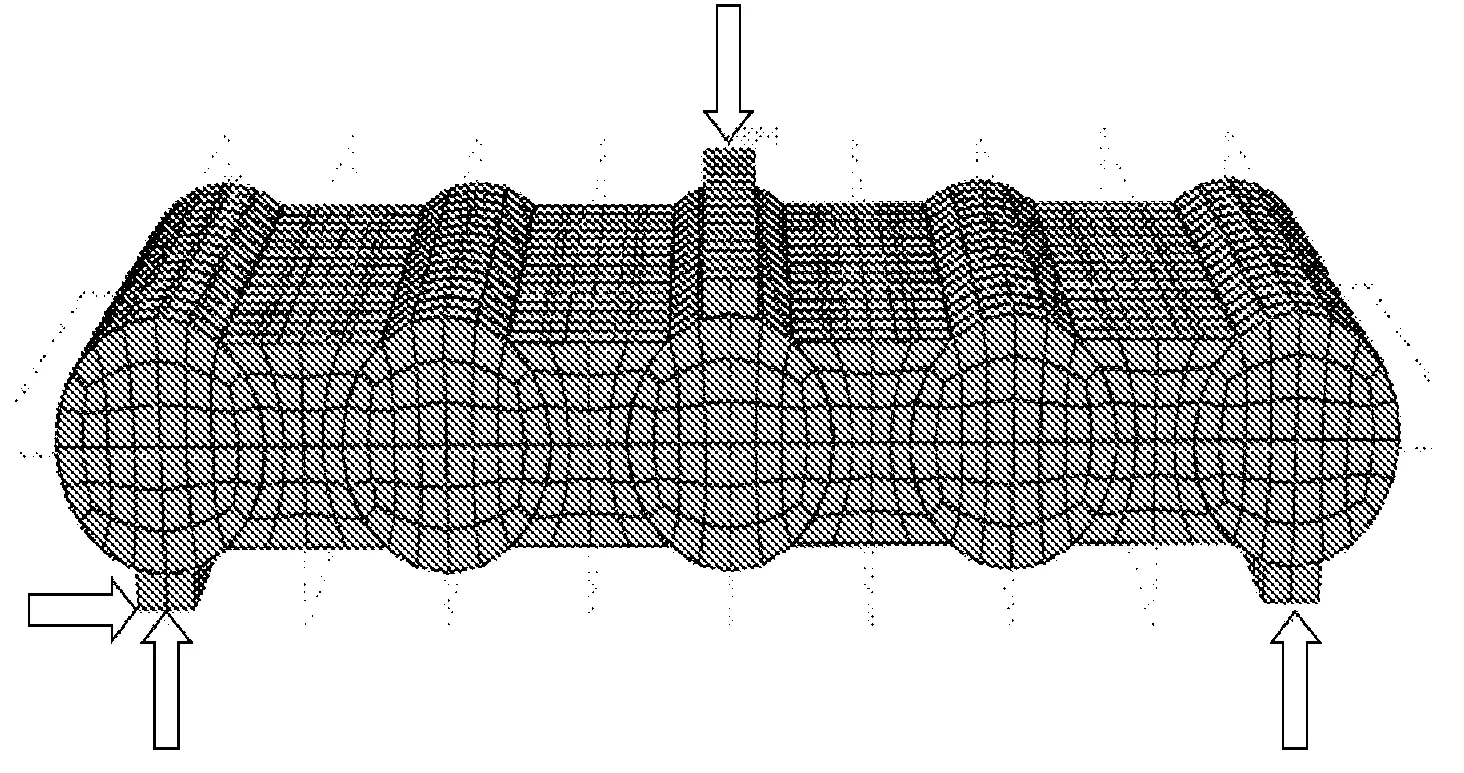
图5 整体模型
选取1∶1模型试验结果与模拟结果,绘制跨中位置荷载-位移曲线,如图6所示,图中实线表示试验结果,虚线表示模拟结果。从图6可以看出,数值模型的初始刚度大于试验的初始刚度,分析原因在于试验中混凝土颗粒之间有空隙,无法达到理想填充状态,所以在试验初期加载时,试验初始刚度要小于数值模拟的初始刚度。
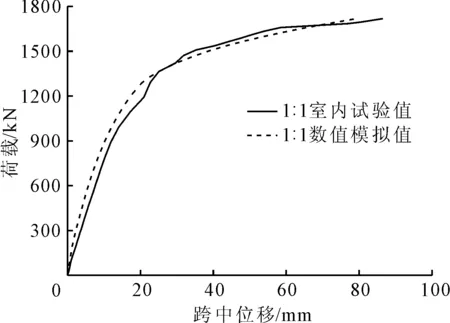
图6 试验值与模拟值对比
由图6可知,1∶1模型选用如上本构模型得到的数值模拟结果与室内试验结果较为吻合,因此,采用该本构模型可以较为准确的反映STS管幕结构的力学性能。
3 STS管幕结构工程机理分析
3.1 模型建立
选取11根钢管按实际尺寸1∶1建模,作为标准构件。采用大型非线性有限元分析软件ABAQUS建立各试验组模型。整个模型包括钢管、翼缘板、横向螺栓、管内混凝土、管间混凝土以及垫板共6个细部构造。本节数值模拟试验模型以室内1∶1试验为参考,支座采取一端固定一端简支的形式。本节模型所选取的材料本构模型及网格划分形式与模型参数标定中的一致。模型细部构造如图7所示,整体模型如图8所示,模型参数如表2所示,数值模拟加载方式见图9。
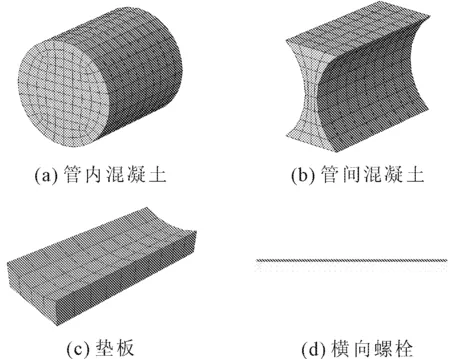
图7 模型细部构造图

图8 整体模型图
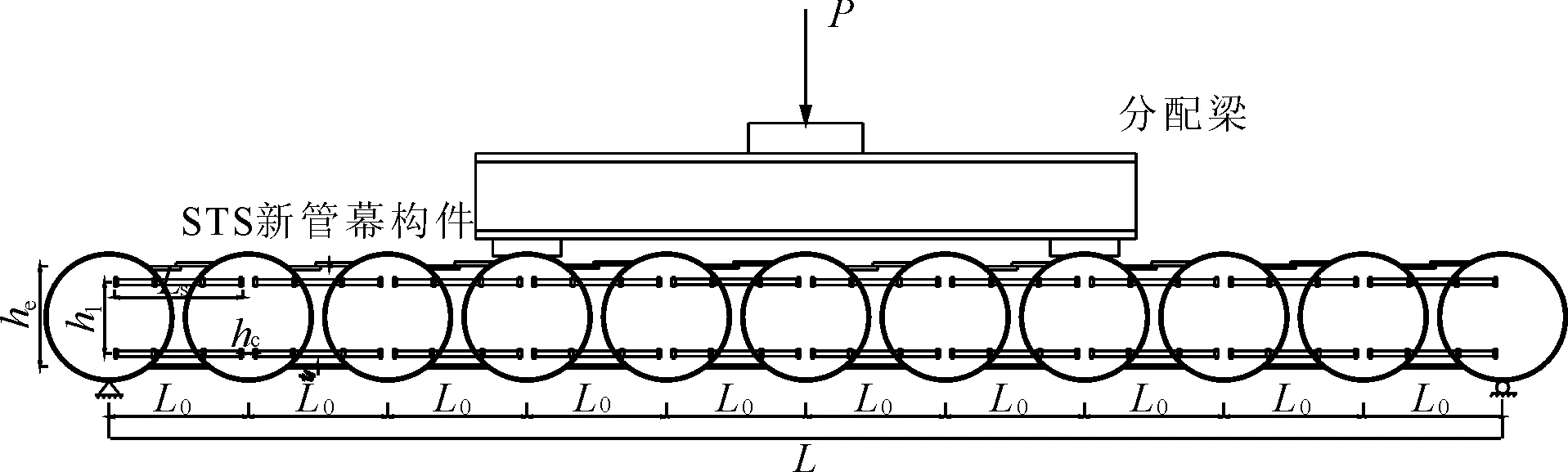
图9 数值模拟试验加载方式
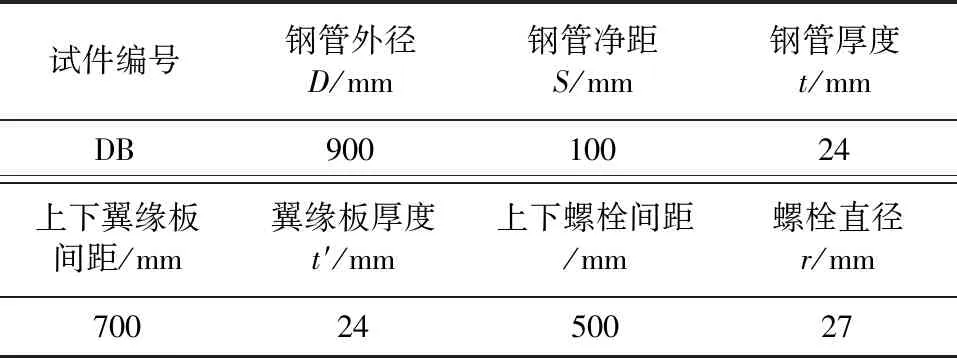
表2 模型参数
3.2 对比组模拟结果分析
经过数值模拟得到STS管幕结构对比组各细部构造在对称集中荷载作用下的应力应变演化规律,以《混凝土结构设计规范》[17](GB 50010—2010)中所描述的混凝土与钢材的应力应变关系为标准,各部件失效标准即为:当C30混凝土拉应力达到1.5 MPa或拉应变达到8.1×10-5、当C30混凝土压应力达到30 MPa或压应变达到1.64×10-3、当钢管应力达到屈服应力235 MPa、当翼缘板达到屈服应力206 MPa、当横向螺栓达到屈服应力500 MPa。以字母A至H分别表示管间受拉区混凝土失效、管内受拉区混凝土失效、钢管底部产生塑性形变、管间受压区混凝土失效、钢管底部屈服、下螺栓屈服、下翼缘屈服、上螺栓屈服,共8个受力节点,以M表示试件破坏。对比组各细部构造失效时所对应的荷载如表3所示。

表3 各细部构造退出工作时的荷载
由表3可知各细部构造按照字母编号顺序先后达到失效标准,进而退出工作,当构件破坏时管内受压区、上螺栓仍然未破坏,下翼缘板未进入塑性阶段。
经过数值模拟得到对比组在对称集中荷载作用下的跨中位移随荷载的变化关系,同时经过计算得到其刚度随荷载的变化趋势,如图10、图11所示。
由图10、图11可知,整个构件的受力阶段基本可以分为三个过程:线弹性阶段(0C)、弹塑性阶段(CD)、塑性破坏阶段(DM)。STS管幕结构极限承载力为3 220.8 kN·m,初始刚度为330.9 kN·m/mm。随着荷载的增大,STS管幕结构的刚度在不断地减小,当管幕结构的各细部构造在不同阶段进入塑性并退出工作时,结构的刚度发生突然下降。并且当钢管底部产生塑性形变(C)、管间受压区混凝土达到峰值压应变(D)、钢管底部屈服(E)时,STS管幕结构刚度变化最为明显。由此可知钢管与管间受压区混凝土对整个构件承载力起到至关重要的作用。
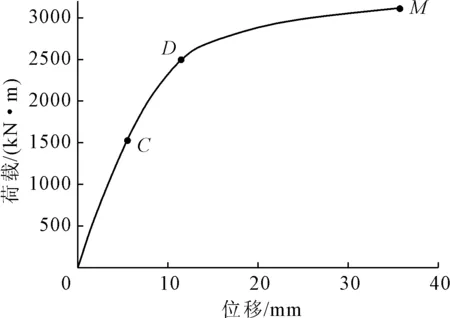
图10 对比组位移-荷载曲线

图11 对比组刚度曲线
结合图10、图11可知,STS管幕结构对比组的工作机理可以分析得到:在结构受力前期,构件基本处于线弹性阶段(0C:0%Pu~50.67%Pu(Pu表示构件的极限承载力)),随着荷载的增加,管间混凝土受拉区和管内混凝土受拉区由于横向螺栓的作用处于受拉状态,并且随着荷载的不断增加而逐渐产生塑性变形,该部分对承载能力的贡献逐渐减弱,并当构件各细部构造进入塑性或退出工作时STS管幕结构的刚度产生突然下降;在该阶段钢管和下翼缘板在荷载作用下处于弹性受拉状态,产生一定的形变;管间混凝土受压区区受力虽然较小,但也已经产生一定塑性形变。
在结构受力中期,构件处于弹塑性阶段(CD:50.67%Pu~89.74%Pu),当荷载达到极限荷载的50.67%时,钢管底部进入塑性阶段,STS管幕结构抗弯刚度产生明显下降,并且分担到管间受压区混凝土的荷载增加,使其应变及塑性形变增大。随着荷载的进一步增加,管间混凝土受压区塑性形变进一步增大,钢管底部大面积屈服,当荷载增大到极限荷载的77.79%时,钢管底部全部屈服,管间混凝土受压区达到峰值压应变,管间受压区混凝土压碎。随着管间受压区混凝土逐渐退出工作,该部分对整个构件承载能力的贡献逐渐减弱,管幕结构的刚度进一步减小。
在结构受力后期,构件处于塑性破坏阶段(DM:89.74%Pu~100%Pu),当荷载增加至极限荷载的89.74%时,构件主要承载部件全部退出工作。当荷载达到极限荷载3 220.8 kN·m时,构件因刚度过小使其在较小荷载增幅的情况下产生过大变形,因而视其破坏。
在整个模拟过程当中,下翼缘板以及上螺栓始终未达到屈服强度。
4 混凝土填充率对STS管幕结构抗弯性能的影响
结合现场施工情况,钢管内及管间掏土困难,其清除效果难以保证,直接影响了STS管幕结构的抗力性能。本节通过建立不同填充率的数值模型,分析得到其在荷载作用下的荷载-位移曲线以及刚度曲线,结合各细部构造的应力应变演化规律,研究混凝土填充率对管幕结构抗弯性能的影响。
4.1 管内混凝土填充率对管幕结构抗弯性能影响
以对比组为参照,选用11根管1∶1模型,分别建立管内填充高度为0%、20%、40%、60%、80%以及100%共6组模型。模型加载同样选用对称集中力逐级加载,选取跨中纯弯段作为研究对象,得到跨中位移和各细部构造的应力应变演化情况,输出其荷载-位移曲线及刚度变化曲线,试验组参数如表4所示,输出结果见图12、图13。
由图12和图13中不同管内填充率时STS管幕结构的荷载位移曲线和刚度曲线可知,随着管内灌注量的不断提升,管幕结构的极限承载力以及抗弯刚度都有不同程度的提升。当管内填充率小于等于40%时,结构延性较差,易发生脆性破坏,当管内填充率大于等于60%时,结构的受力情况逐渐转为弹性阶段、弹塑性阶段以及塑性破坏阶段,且延性逐渐增强。
表4 管内混凝土填充率变化试验组参数
当填充率小于等于20%时,下螺栓无法锚固于管内混凝土中,管内混凝土易脱落,钢管顶部容易屈服,最终极限承载力及刚度被严重削弱,破坏时钢管呈鸭蛋形状;当填充率介于40%~60%时,下螺栓可以锚固于管内混凝土中,填充料为40%时钢管顶部容易屈服,管内混凝土表面容易被压碎,当填充率为60%时,钢管顶部不再发生屈服,转为钢管底部屈服但极限承载力及刚度同样削弱严重,当填充率为80%时,构件拥有较为明显的弹性阶段、弹塑性阶段以及塑性破坏阶段。因管内留有空隙,整个管幕结构承载力及刚度也一定程度上被削弱;当管内混凝土无法填充全部空间时,由于钢管顶部无填充物支撑,使该位置刚度较小,从而造成上翼缘板对管间混凝土的约束作用减弱,使其无法抵抗钢管对管间混凝土中部的劈裂作用,最终导致管间混凝土由上至下出现受压、受拉、再受压、再受拉的四个受力区域。
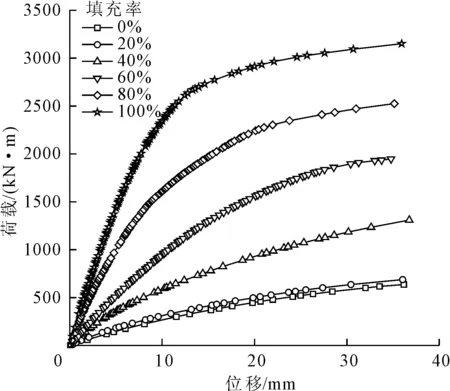
图12 管内不同填充率时管幕结构荷载-位移曲线
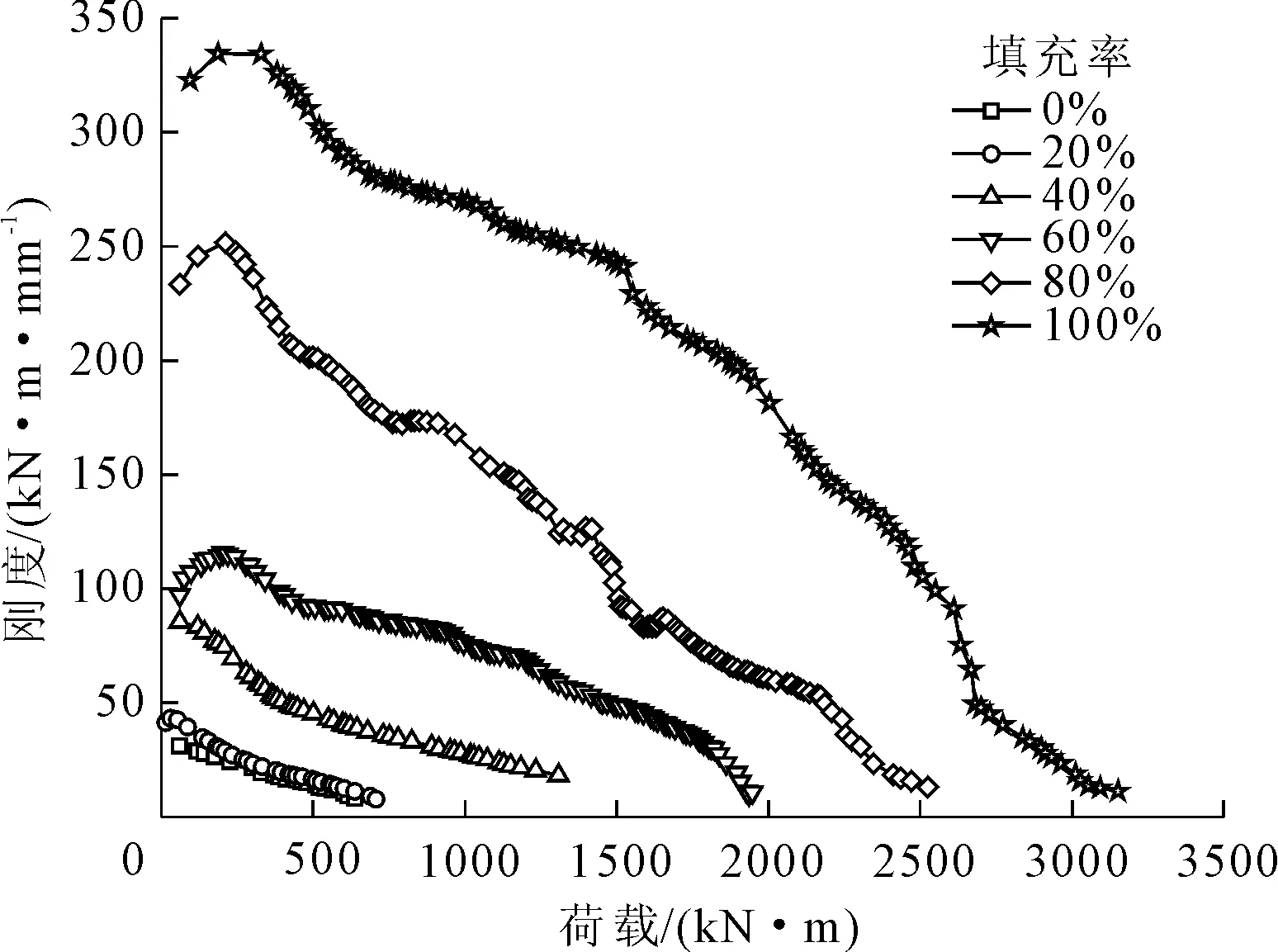
图13 不同管内填充率时整体结构刚度曲线
4.2 管间底部混凝土填充率对管幕结构抗弯性能的影响
以对比组为参照,选用11根管1∶1模型,分别建立管间底部填充高度为20%、40%、60%、80%以及100%共5组模型。模型加载同样选用对称集中力逐级加载,选取跨中纯弯段作为研究对象,得到跨中位移和各细部构造的应力应变演化情况,输出其荷载-位移曲线及刚度变化曲线,分析STS管幕结构各细部构造的破坏形式及先后顺序,以此研究钢管之间填充率对管幕结构抗弯性能的影响。试验组参数同表4所示,以40%填充率模型为例,其管间残留土体以及混凝土模型效果如图14所示。
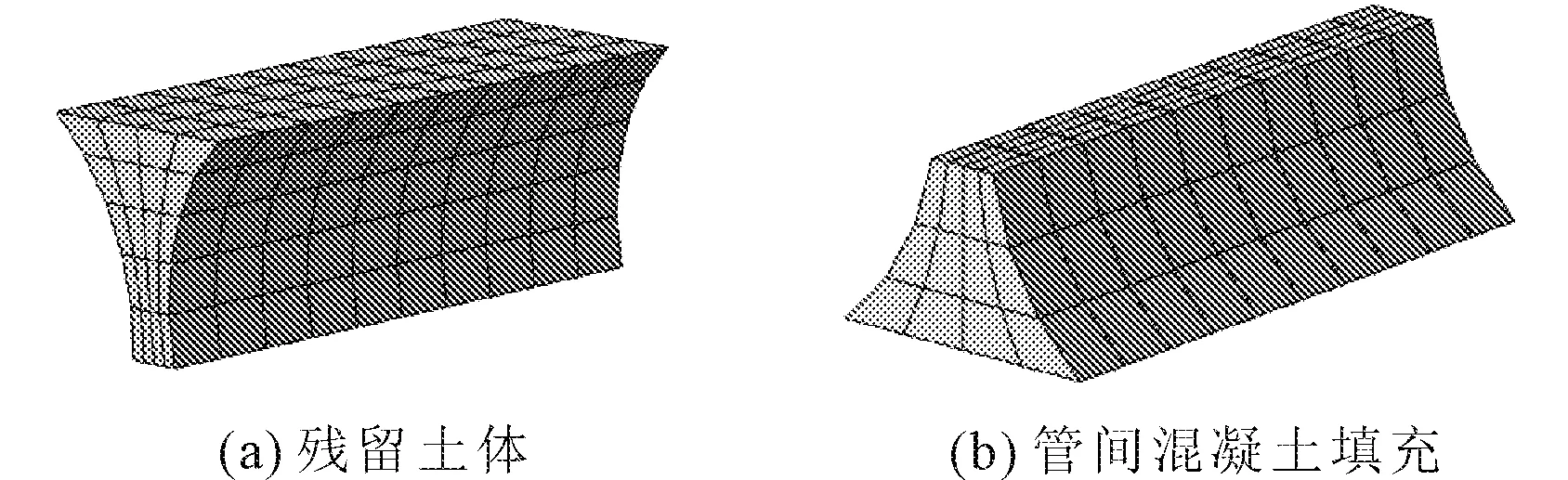
图14 填充40%时管间土体和混凝土效果图
图15和图16分别表示不同管间底部混凝土填充率条件下STS管幕结构的荷载位移曲线和刚度曲线。由图可知,随着管间底部灌注量的不断提升,管幕结构的受力形式发生了改变,极限承载力以及抗弯刚度也有不同程度的提升。当管内填充率小于等于40%时,结构只存在弹性阶段以及塑性破坏阶段,当荷载达到900 kN·m时,构件刚度直接下降85.14%,并直接从弹性阶段跳跃至塑性破坏阶段。当管内填充率大于等于60%时,结构的受力情况逐渐转为弹性阶段、弹塑性阶段以及塑性破坏阶段。随着管间底部混凝土填充率的不断增长,构件的极限承载力及抗弯刚度都有不同程度的提升。
当填充率小于等于40%时,受压区无混凝土承受压力,所有荷载由上螺栓承担,当其屈服之后,整个结构的抗弯刚度直接下降至初始刚度的十分之一,并使结构直接从弹性阶段跳入塑性破坏阶段,这也是填充率小于40%时,荷载-位移曲线有一个突变(尖角),即刚度突然变形的原因;当填充率大于等于60%时,结构存在明显的弹性阶段、弹塑性阶段以及塑性破坏阶段。随着受压区混凝土占有率的不断提升,结构的承载力及刚度不断提升,但上螺栓仍然为受压区的主要承载部件,因此上螺栓依然先于钢管底部产生破坏;管间混凝土与残留土体交界面容易产生应力集中,当荷载增至90%Pu时,管间混凝土交界面被压碎。整个过程中残留土体所受荷载较小,变形较大。

图15 管间底部不同填充率时管幕结构
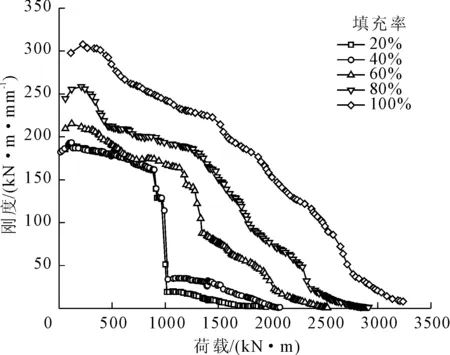
图16 管间底部不同填充率时管幕结构刚度曲线
4.3 管间顶部混凝土填充率对管幕结构抗弯性能的影响
以对比组为参照,选用11根管1∶1模型,分别建立管间顶部填充高度为20%、40%、60%、80%、90%以及100%共6组模型。模型加载同样选用对称集中力逐级加载,选取跨中纯弯段作为研究对象,得到跨中位移和各细部构造的应力应变演化情况,输出其荷载-位移曲线及刚度变化曲线,分析STS管幕结构各细部构造的破坏形式及先后顺序,以此研究钢管之间顶部混凝土填充率对管幕结构抗弯性能的影响。试验组参数同表4所示,以40%填充率模型为例,其管间残留土体以及混凝土模型效果如图17所示。
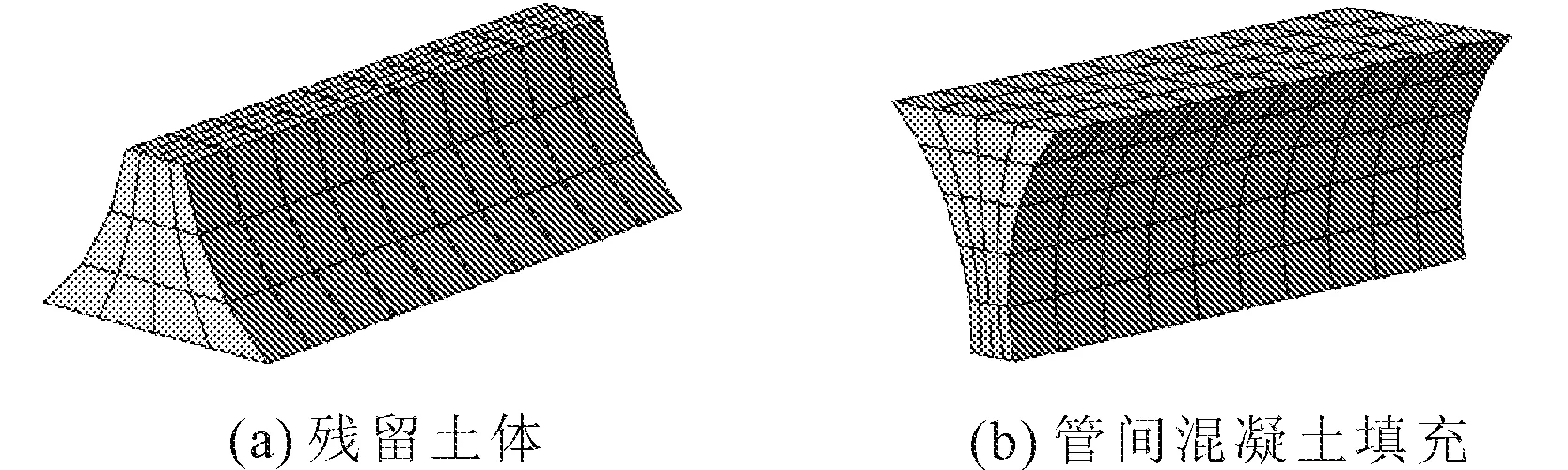
图17 填充40%时管间土体和混凝土效果图
图18和图19分别表示不同管间顶部混凝土填充率条件下STS管幕结构的荷载位移曲线和刚度曲线。由图可知,当管间顶部混凝土填充率超过20%时,填充率的变化对STS管幕结构抗弯性能的影响较小。所有构件都经历了弹性阶段、弹塑性阶段以及塑性破坏阶段。

图18 管间顶部不同填充率时管幕结构

图19 管间顶部不同填充率时管幕结构刚度曲线
管间顶部混凝土填充率超过20%时,可以保证STS管幕结构的抗弯性能与其满填状态下的差异在较小的范围之内,因此在实际工程中,可以通过减少管间底部土体的清除,在保证抗弯性能基本不变的前提下减少工作量与操作难度,以节约材料,缩短工期,减少造价。
5 结 论
(1) STS管幕结构在对称集中荷载作用下,各细部构造失效过程按照管间受拉区混凝土、管内受拉区混凝土、钢管底部(产生塑性形变)、管间受压区混凝土、钢管底部(屈服)、下螺栓的顺序进行,整体结构抗弯刚度也随之下降。
(2) 当填充率小于等于20%时,由于缺少下螺栓的约束作用,管内混凝土易脱落,当填充率小于等于40%时,钢管部分受压区荷载全部由钢管承担,当钢管顶部屈服时构件破坏并且钢管呈“鸭蛋形”,管内混凝土上表面与钢管连接处易被压碎;当填充率大于等于60%时,管内受压区混凝土可以有效分担钢管顶部所受的荷载,因此钢管顶部不再发生屈服。
(3) 当管间底部混凝土填充率小于等于40%时,管间受压区荷载基本由上螺栓承担,因此当上螺栓首先发生屈服时,结构受力阶段直接跳入塑性破坏阶段;当填充率大于等于60%时,管间受压区混凝土有效分担上螺栓所承受的荷载,结构受力阶段重新恢复弹塑性阶段。

