基于波段加权K均值聚类的高光谱影像分类
李 玉,甄 畅,石 雪,赵泉华
(1.辽宁工程技术大学 测绘与地理科学学院 遥感科学与应用研究院,辽宁 阜新 123000;2.桂林理工大学 测绘地理信息学院,广西 桂林 541000)
0 引言
由于高光谱遥感自身的特点,使得其一直是遥感领域的研究热点之一[1-2]。高光谱遥感影像在众多领域中具有广泛的应用,包括农业、林业、海洋、矿石及大气成分研究等领域[3-8]。由于高光谱影像内包含了比较丰富的光谱信息,对地物目标的精细、精准分类及提取、理化、生物参数的反演提供了数据支撑和保障,所以其是定量对地观测最具潜力的新一代数据源[9-10]。然而,由于高光谱影像包含众多的波段,将波段看作特征,在解译时会有休斯现象,从而导致“维数灾难”,如何充分合理利用光谱特征是亟待解决的问题[11]。
近年来,有效利用高光谱影像内光谱特征信息的方式分为2种:第一种方式为直接采用所有光谱特征,这种方式是将所有特征看作一个整体,最具代表性的算法是光谱角分类法,该方式对于特征的冗余问题无法避免[12-14];第二种方式为通过处理运用部分光谱特征,这种方式包括降维和波段选择两大类。对于降维方法,经典的有主成分分析法、独立成分分析法及线性判别分析等,该类方法无法确定具体运用原始特征空间的哪一部分[15-20]。对于波段选择方法,有学者提出了利用人工蜂群进行波段选择及基于流形波段选择方法等,该类方法只能硬性选择出一部分波段运用到后续的工作中,其他波段的信息都无法利用[21-24]。因此,本文将特征加权思想引入K均值算法以有效地利用波段信息,通过构建不同的权重以表达出高光谱影像各波段的重要性[25]。
1 算法描述
1.1 分类模型
设高光谱影像为z= {zn,n= 1,2,…,N} = {z(d),d= 1,2,…,D},其中,n为像素索引;N为总像素数;d为波段索引;D为总波段数;zn=(znd,d= 1,2,…,D)T为像素n的光谱测度矢量,znd为像素n在d波段的光谱测度;z(d)= {znd,n= 1,2,…,N}为d波段的光谱测度集合;T为矩阵的转置符号。
在采用K均值算法进行影像分类时,通常影像各波段对分类结果起到的作用一致且波段间独立[26-27]。由于高光谱影像的休斯现象十分明显,所以对高光谱影像直接运用K均值算法不能避免维数灾难现象。对于高光谱影像,需要考虑各波段含有信息量及波段间的相关性等因素。为此,通过对各波段赋予不同的权重以有效地利用各波段的光谱特征,进而解决高光谱影像的分类问题。
建立具体目标函数为:
(1)

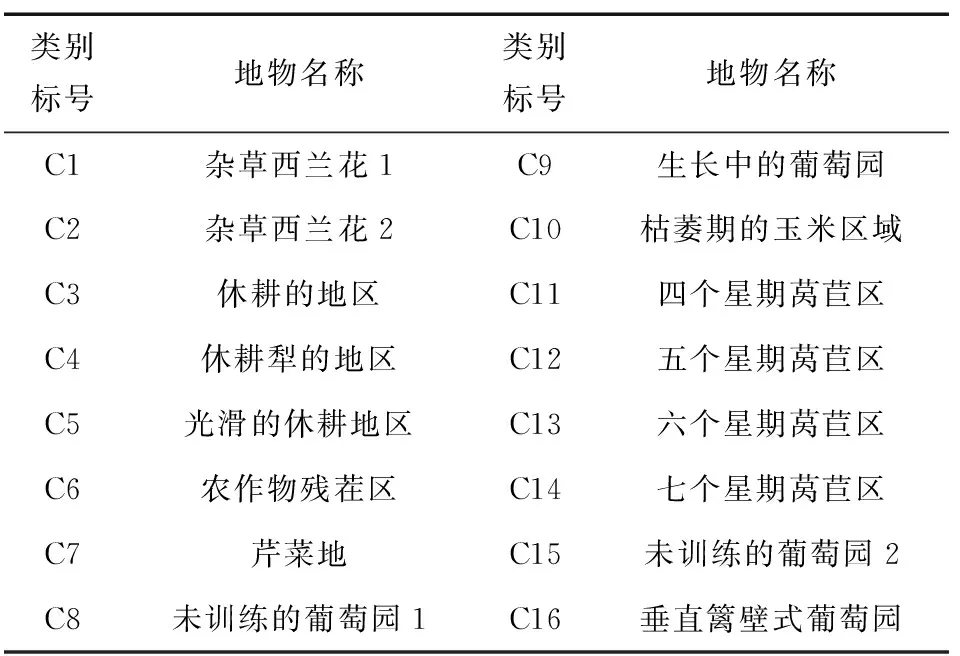
受成像条件的影响,高光谱影像有少部分波段不益于影像分类,所以该部分波段的波段权重应为0。可以通过各波段影像直方图的分布情况来确定这部分波段[28]。设各波段影像的直方图中频率非0数的集合为h= {hd,d= 1,2,…,D},其中,hd= # {osd≠ 0,s∈{0,1,…,255}},osd= # {n,znd=s}。给定阈值T,当hd 对于剩余波段,由于各波段信息量及波段间相关关系都对分类结果产生影响,所以这两个因素决定剩余波段的波段权重,以表达其对聚类的重要性。 在影像中,熵信息是对影像不确定性即信息量的度量。因此,提出算法采用熵值的大小表示高光谱影像内各波段的信息量度量[29-31]。定义波段d熵值表示为: (2) 式中,令熵值矢量表示为E=(Ed,d= 1,2,…,D);pg表示灰度值为g且频率不为0的概率: (3) 在待分类影像中,均值表示了影像内像素光谱测度的平均水平,标准差表示了影像内像素光谱测度的离散程度。为了避免于标准差中所包含的平均水平的影响,采用均值与标准差的比值表示影像内像素光谱测度关于离散程度上的信息量[32]。将波段d的像素光谱测度标准差表示为: (4) 式中,令各波段内像素光谱测度标准差的集合表示为σ= {σd,d= 1,2,…,D},令u={ud,d=1,2,…,D}表示为各波段像素光谱测度均值的集合,ud为波段d内像素光谱测度的均值,可表示为: (5) 在高光谱影像中,通常采用互信息来表示影像内2个波段内像素之间的相关关系[33-34]。设高光谱影像的互信息矩阵为R,设d波段影像z(d),其与d±1波段的互信息分别为Rd,d+1,Rd,d-1,其中: Rd,d±1=Ed+Ed±1-Ed,d±1, (6) 式中,Ed,d±1为波段d与d+1及d与d-1的联合熵: (7) 综上,定义波段权重wd为: (8) 式中,A,B为调节参数,分式上方和下方分别为信息量函数和相关性函数。提出算法中将调节参数A,B分别取大于0,以保证w与信息量函数呈正相关,与相关性函数呈负相关。若B取值越大,则波段权重的变化范围受波段信息量的影响越大,而对影像分类起主要作用的波段数量则越少。当B=7时,仅存在少数波段的权重值较大,导致分类结果精度较低。为了提高对影像分类起主要作用波段的数量,选取参数B的取值范围为(0,7]。参数A的取值大小反映了波段之间相关性对波段权重的影响,若数值越小则相关性对波段权重的影响程度越大。为了增大各波段之间波段权重的差异,选取参数A的取值范围为(0,4]。 (9) 式中, (10) 得到amd的取值范围为amd∈[0.000 3,1]。 为了实现高光谱影像分类,最小化目标函数J以局部优化r,x,a,获得各参数的估计值,即: (11) 参数求解过程描述如下: ① 求解r。像素隶属于各类别的非相似性测度越小为1,表示该像素隶属于对应的类别,因此将r的表达式定义为: (12) ② 求解x。利用函数J对xmd求偏导,令其为0,通过求解可得到x的表达式,具体过程为: (13) 则xmd的具体表达式为: (14) ③ 求解a。利用拉格朗日乘数法求解amd。已知z,x,r,w和λ,构建带有约束条件的新目标函数,表示为: (15) 式中,vm为拉格朗日因子。利用函数L对amd求偏导,并令其为0,根据其自身的约束条件可求得amd的具体表达式为: (16) 总结提出的波段加权K均值聚类影像分类算法的实现过程: ① 设置阈值T,ε1>0,ε2>0以及当循环次数达到LOOP时停止迭代;设置初始聚类中心矢量集x(0)和波段-类别权重矢量集a(0); ② 根据式(2)、式(4)和式(5)分别计算各波段的熵值E、标准差σ及均值u; ③ 根据式(6)计算互信息矩阵R; ④ 根据式(8)确定波段权重矢量w; ⑤ 根据式(12)计算聚类隶属矢量集r(t+1); ⑥ 根据式(14)计算聚类中心矢量集x(t+1) ⑦ 根据式(9)和式(10)计算规则化项λ(t+1); ⑧ 根据式(16)计算波段-类别权重矢量集a(t+1); ⑨ 如果|xmd(t+1)-xmd(t)|<ε1且|amd(t+1)-amd(t)|<ε2或t=LOOP,则停止迭代;否则迭代次数增加,并转⑤。 为了验证提出算法对高光谱影像分类的有效性,利用MATLAB软件编程以实现高光谱影像分类。实验选用了AVIRIS数据,影像内呈现的是Salinas地区,空间分辨率为3.7 m,尺寸为512 pixel×217 pixel,光谱测量范围为400~2 500 nm,实验中去除水吸收波段共20个,采用204个波段进行实验,利用34,18,11波段填充红、绿、蓝波段构成真彩色影像,如图1(a),图像中包括16类地物目标,如表1所示。图1(b)为高光谱影像的标准分类图。 图1 Salinas真彩色影像与标准分类图Fig.1 True color display image and standard classification image of Salinas 表1 高光谱影像的类别标号和地物名称Tab.1 Labels and ground features of hyperspectral images 由于本文中类别为16,则选择阈值T为15。对于本文使用的高光谱影像来说,采用控制变量法来确定A和B最合适的取值。根据总精度变化情况,本文取A为2,B为2.5最合适。 采用对比算法和提出算法对高光谱影像进行分类得到的结果如图2所示。其中,图2(a)为K均值算法获得的高光谱影像分类结果,图2(b)为提出算法获得的高光谱影像分类结果。 图2 高光谱影像分类结果Fig.2 Classification results of hyperspectral images 从视觉上看,K均值算法将C1和C2类分成了一类,将C10和C11类分成了一类,C8和C15类区域错分成了4个类别。本文算法将C1和C2类部分区域分开,将C10和C11类分开,将C3类的大部分区域分了出来。 对比算法和提出算法分类结果的精度如表2所示,以定量评价提出算法的分类效果。通过比较各分类算法的结果影像与标准分类影像可得到关于各类别地物的混淆矩阵,并以此可以计算出分类结果的各个精度值。结合分类精度和分类结果可知,导致分类精度比较低的原因是影像中存在同物异谱和异物同谱现象,主要代表类别为C3,C8,C15类,尤其是C8和C15类之间,其异物同谱及同物异谱现象十分明显;C3类中,上半部分与C5类异物同谱,下半部分与C12类异物同谱。由于本文方法是根据光谱进行分类,所以这种光谱相近的类别很难分开。在实验中,对高光谱影像分别运用K均值算法、本文算法以及将本文算法中求得的w取倒数进行分类,对应的总精度分别为54.73%,78.08%,47.77%,由此可见引入w的有效性。 表2 高光谱影像分类结果精度评价 本文提出了一种融合波段加权的高光谱影像分类算法,提出算法为了有效地利用高光谱影像的波段信息,将特征加权思想引入到K均值算法中,该思想提供了一种数据变换的方式,同时通过特征权重的定义提供将对地物目标的认知融入算法模型的途径。该方法也算是提供了一种新的降维方式,打破了传统硬性的波段选择方式,通过波段权重来定义波段的重要性。在未来的工作中,需要考虑如何根据具体的任务对特征加权。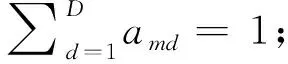
1.2 模型求解

2 高光谱影像的分类实验和讨论



3 结束语

