基于双驱动DP-MZM的倍频双啁啾信号产生方法①

张 昆，赵尚弘，林 涛，王国栋，李 赫，李 轩，朱子行

(空军工程大学信息与导航学院，西安 710077)

0 引言

线性调频(LFM)信号具有大的时宽带宽积和优良的脉冲压缩特性，可同时提高雷达的测距和测速精度，以及距离和速度分辨率，被广泛应用到现代雷达系统中[1-3]。然而单啁啾LFM信号存在“刀刃状”的模糊函数，导致了雷达在探测运动目标时，存在位置-多普勒模糊问题[4]。为了解决这个问题，雷达可以采用双啁啾LFM信号。双啁啾LFM信号在时域中，波形由两个啁啾相反单啁啾LFM信号的波形干涉而成；在频域中，单个脉冲持续时间里存在两条啁啾相反的扫频直线。微波信号通常由电学方法产生，如LC振荡电路、石英晶体、高品质的射频微波腔及直接数字合成技术等。然而电子瓶颈导致了电学方案产生的双啁啾信号载频较低，通常受限于20 GHz，带宽也受限于 GHz 量级，从源头上限制了雷达性能的提升。随着毫米波、太赫兹(THz)技术的发展，信号的载频和带宽需求逐渐增加。微波光子技术能直接产生、实时处理更高载频、更宽带宽、更大调谐范围的雷达信号，有望为雷达系统发展和军事斗争演化带来技术性和体制性变革[5-7]。

2015年，基于双平行马赫增德尔调制器(DP-MZM)的方案受限被提出，产生了双啁啾信号[8]。方案中，DP-MZM分别受微波和基带信号驱动，生成载波抑制双边带光信号，光电转后产生双啁啾信号。方案产生的信号载频被上转换到驱动射频信号，带宽被扩展为驱动基带信号的二倍。然而，由于方案缺乏倍频操作，产生信号的载频仍受限于驱动微波信号。为了扩展倍频系数，基于双驱动马赫增德尔调制器或双偏振正交相移键控调制器被提出，产生了载波带宽同步倍频的双啁啾LFM信号[9-11]。此外，双啁啾LFM信号也可以通过傅里叶锁模光电振荡器(FDML OEO)产生[12]。方案中，光源的中心频率受到三角波电流控制，为了保证系统模式稳定，采用了分布式反馈激光器。为了防止链路中长距离光纤传输时，色散导致的信号功率衰落，OEO链路中还加入了负色散光纤，补偿光纤引入的色散相移。由于采用了FDML技术，方案可突破OEO的振荡建立时间，产生大时宽带宽积的双啁啾LFM信号。此外，由于信号相位和频率呈微分关系，当采用外电光相位调制技术为两路光信号，引入抛物线相位差时，光电转换后，也可以产生双啁啾信号[13-14]。为了扩展信号的带宽，可以采用抛物线分割方案，2020年中科院半导体所实现了带宽5倍频双啁啾LFM信号的产生[15]。上述方案都采用光学方案实现了双啁啾LFM信号的产生，但存在带宽和载频倍频系数有限的问题。

本文提出一种基于双驱动DP-MZM的载波二倍频、带宽四倍频双啁啾LFM信号的产生方法。方案中，DP-MZM的上臂受射频驱动，产生偶数阶光边带；下臂受基带信号调制，产生单边带光信号。合理地设置驱动信号的调制系数和主调制器的直流相移，可抑制DP-MZM输出光信号中的载波分量。耦合光信号平方率检波后，可产生载波二倍频、带宽四倍频的双啁啾LFM信号。方案产生的双啁啾LFM信号载频受驱动微波信号调谐，带宽受驱动基带信号调谐。所提方案无需偏振器件和光滤波器，具有操作简单、调谐性高的特点，同时具有参数可调谐、信号可重构的优势，可为新一代雷达提供可靠的信号源系统。

1 系统原理

图1 基于双驱动DP-MZM的倍频双啁啾LFM信号产生方案

图1为基于双驱动DP-MZM的倍频双啁啾LFM信号产生方案。方案的核心器件为双驱动DP-MZM，由两个双驱动MZM和一个主MZM组成。光源(LD)产生连续波光信号，通过偏振控制器(PC)注入DP-MZM，子MZM1受射频驱动，子MZM2受基带LFM信号驱动，上下两臂调制光信号通过主MZM3耦合输出。耦合光信号经掺饵激光放大器(EDFA)放大后注入PD完成光电转换，即可生成载频-带宽倍频系数2-4的双啁啾LFM信号。

在DP-MZM的上臂中，MZM1受微波驱动，工作在MATP，输出光信号的光域表达式为：

exp(-jm1cosωRFt)]

(1)

式中，Ec和ωc分别为光源输出信号的幅度和角频率，m1=πVRF/Vπ为MZM1的调制系数，VRF和ωRF为射频信号的峰值电压和角频率，Vπ为DP-MZM子调制器的半波电压。

利用Jacobi-Anger展开式(1)，可得：

EM1(t)=Ecexp(jωct)[J0(m1)+

(2)

在小信号模型条件下忽略二阶以上边带，式(2)可近似等于：

EM1(t)≈Ecexp(jωct)[J0(m1)-J2(m1)exp(j2ωRFt)

-J2(m1)exp(-j2ωRFt)]

(3)

在DP-MZM的下臂，MZM2受基带LFM信号驱动，工作在MATP，输出光信号的光域表达式为：

+exp(-jm2coskt2)]

(4)

式中，m2=πVlfm/Vπ为MZM2的调制系数，Vlfm和k分别为基带信号的峰值电压和啁啾率。

利用Jacobi-Anger展开式(4)，在小信号模型下，忽略了二阶以上边带，式(4)可近似等于：

EM2(t)≈Ecexp(jωct)[J0(m1)-J2(m1)exp(j2kt2)

-J2(m1)exp(-j2kt2)]

(5)

从式(5)可以看出，对于扩展频谱调制，其调制结果与单音射频信号调制过程相同。

MZM1和MZM2输出光信号通过主MZM耦合，直流偏置相移为θ时，DP-MZM输出光信号可表示为：

Eout(t)=EM1(t)+EM2(t)exp(jθ)

(6)

设置主MZM工作在MITP，即直流相移θ为π，为了抑制输出信号的光载波，应满足m1=m2。此时，DP-MZM输出为基带和射频调制的二阶CS-DSB光信号。

CS-DSB光信号经EDFA放大后，注入PD完成光电转换，产生光电流为：

(7)

式中，G为EDFA的光增益，η为PD的响应度。在式(7)中，产生的光电流包含了双啁啾LFM信号，中心频率为2ωRF，是驱动射频信号的二倍；当驱动基带信号周期为T时，对应带宽为kT/π，双啁啾信号的带宽增加为4kT/π。因此，方案产生了载波-带宽倍频系数2-4的双啁啾LFM信号。此外，式(7)中，产生的光电流中还包含了直流分量、基带信号cos(4kt2)和载波四倍频射频信号cos(4ωRFt)。这些干扰信号的载频远离所需的双啁啾信号，可利用滤波器滤除。同时，在实际应用中，由于天线的辐射特性，直流分量和基带信号无法辐射到自由空间，而高频杂散信号由于PD的响应带宽而滤除。因此所提方案产生了载波-带宽扩展系数2-4的双啁啾LFM信号，信号的载频受驱动射频调谐，带宽受驱动基带信号调谐。

方案产生的倍频双啁啾LFM信号，其探测性能可通过模糊函数检验。模糊函数表示为信号的时间-频率复合自相关积分的平方，反映了雷达的距离分辨力和速度分辨力。理想信号的模糊函数应该为原点处无限窄而其他处均为0的单个窄尖峰。在图2(a)中，除了多目标在原点处无法分辨外，其他位置均无距离和多普勒模糊。当多目标位于原点以外位置时，雷达系统可提供任意高的速度和位置测量精度，能分辨空间位置非常临近的多目标。

然而，由于模糊函数在原点存在有限的峰值，理想的原点冲激模糊函数在物理无法实现。“图钉状”模糊函数除在原点附近，存在距离-多普勒模糊外，其他位置均可为雷达提供好的速度和位置精度，是理想模糊函数的近似形式。图2(b)为"图钉状"模糊函数示意图，主要由原点窄尖峰组成，尖峰的多普勒轴宽度与信号的带宽成反比，时间轴宽度与信号的时宽成反比。因此，为了提高雷达系统的探测性能，除了需要信号具有“图钉状”模糊函数外，还需具有大TBWP特性。

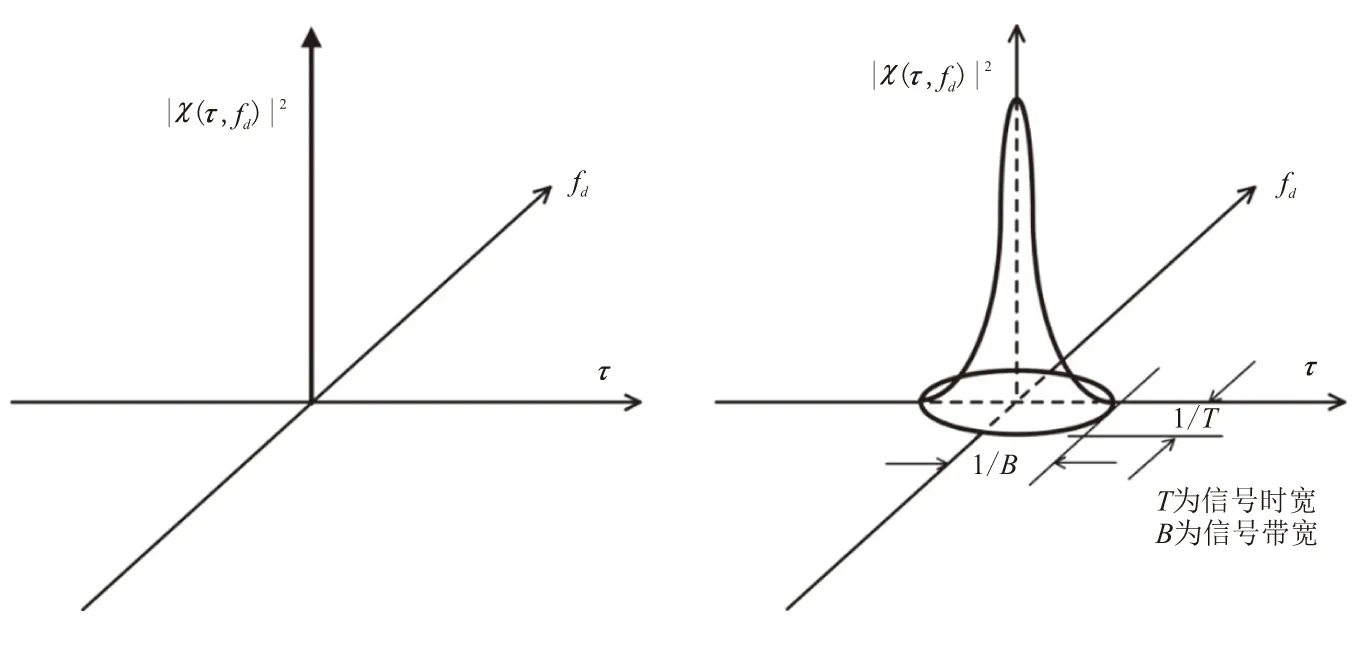
(a) (b)

对于时宽T、啁啾率k的单啁啾LFM信号，其模糊函数可表示为：

|χ(τ，fd)|2=

(8)

式中，±表示单啁啾LFM信号的啁啾符号。

对于时宽T、啁啾率k的双啁啾LFM信号，其模糊函数可表示为：

(9)

从式(8)和式(9)可以看出，双啁啾信号的模糊函数由两个啁啾相反LFM信号的模糊函数组成。双啁啾LFM信号模糊函数在原点处存在窄尖峰，而其他刀刃位置的模糊度降低到1/4，距离-速度探测精度得到了显著的改善。此外，LFM信号调制方式简单，战场中易于被截获，降低了雷达系统的安全性和保密性。而双啁啾LFM信号，是一种复合调制方式，可有效提高雷达系统的探测精度和对抗性能。

2 实验验证结果分析

基于图1的倍频双啁啾信号产生方案搭建实验系统，如图3所示。实验中，光源(Emcore1782)输出波长1551.327 nm、功率15 dBm的线偏振连续光波，通过PC注入DP-MZM(Sumitomo，T.SBZH1.5-20PD-DAC)。DP-MZM的插入损耗为9 dB，消光比为30 dB，半波电压为4 V。射频信号由微波源(R&S SMBV100A)产生，频率设置为7 GHz；基带信号由任意波形发生器(AWG7802)产生，时宽和带宽分别设置为1 μs和400 MHz；调制器偏置电压受直流源(Agilent E3631A)控制，子MZM1和子MZM2工作在MATP，主MZM3工作在MITP。DP-MZM输出光信号通过PD(Agilent 1192A)完成光电转换，产生倍频双啁啾LFM信号。实验中，光谱仪(Advantest Q8384)测量精度为0.01 nm，示波器(DSOV334)采样率为 80 GSa/s，频谱仪(Rohde Schwarz FSV30)带宽为30 GHz，分辨带宽(RBW)设置为100 kHz，分别记录双啁啾信号产生实验中光谱、波形和频谱。

设置DP-MZM上下臂调制系数都为1.2，输出光谱如图4所示。光谱中主要由射频和基带调制二阶边带组成。由于调制器消光比不理想，光谱图中还存在±1阶射频光边带，功率抑制比为25.5 dB。同时，由于采用了较大的调制系数，±4光边带也被激发出来，高阶边带抑制比为31.5 dB，满足实验需求。

图3 基于双驱动DP-MZM的倍频双啁啾LFM信号产生实验

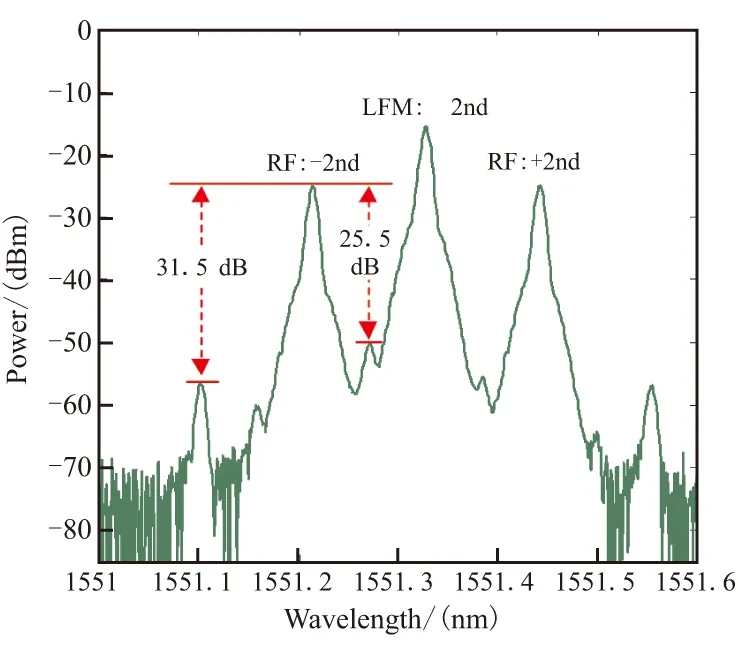
图4 DP-MZM输出光谱

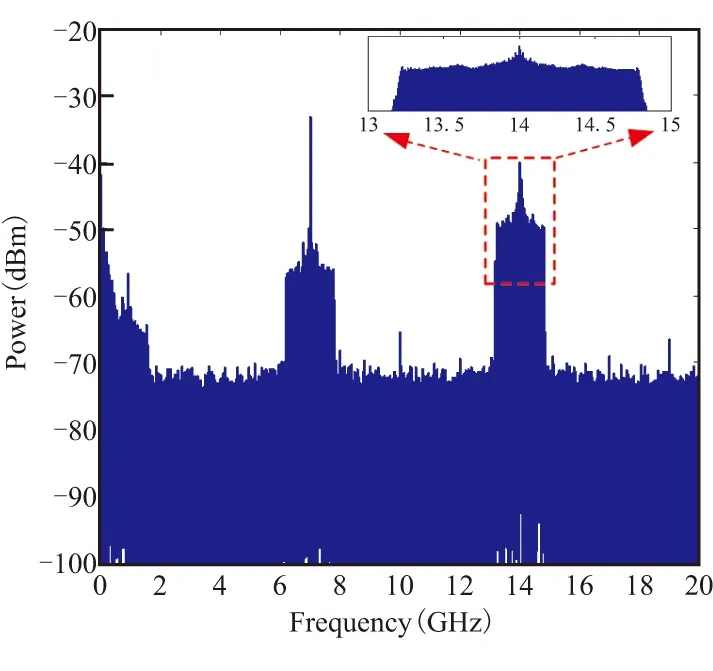
图5 PD输出频谱。插图为双啁啾LFM信号电谱

DP-MZM输出光信号注入PD完成光电转换，拍频信号电谱如图5所示，主要包含直流、基带信号、7 GHz杂散射频信号和14 GHz双啁啾信号。图5中给出了电谱14 GHz处的放大图，可以看处，双啁啾信号中心频率为14 GHz，带宽为1.6 GHz(13.2-14.8 GHz)，分别为驱动射频和基带信号的二倍和四倍，与理论分析相符。此外，由于调制器有限的消光比，7 GHz处出现了杂散信号，这一问题可通过使用高消光比DP-MZM改善。

PD拍频信号滤除杂波后，图6(a)为产生的载波-带宽倍频系数2-4的双啁啾LFM波形。利用短时傅里叶变换(STFT)提取信号的频时曲线。在图6(b)中，时频图中包含两条中心频率14 GHz、啁啾率0.8 GHz/μs和-0.8 GHz/μs的互补频时曲线，对应频率变化范围14-14.8 GHz与14-13.2 GHz的正、负啁啾LFM信号。双啁啾信号的带宽为1.6 GHz，对应TBWP可计算为1600。同时，时频图中还存在其他杂波频率，如啁啾率0.4 GHz/μs和-0.4 GHz/μs的LFM信号，和14 GHz射频信号。该问题是由于调制器有限消光比，导致了射频±1阶和基带±1光边带未能完全抑制，拍频后出现了杂散信号。

(a)

(b)

为了验证信号的探测性能，图7给出了信号单周期的波形和对应的自相关结果。

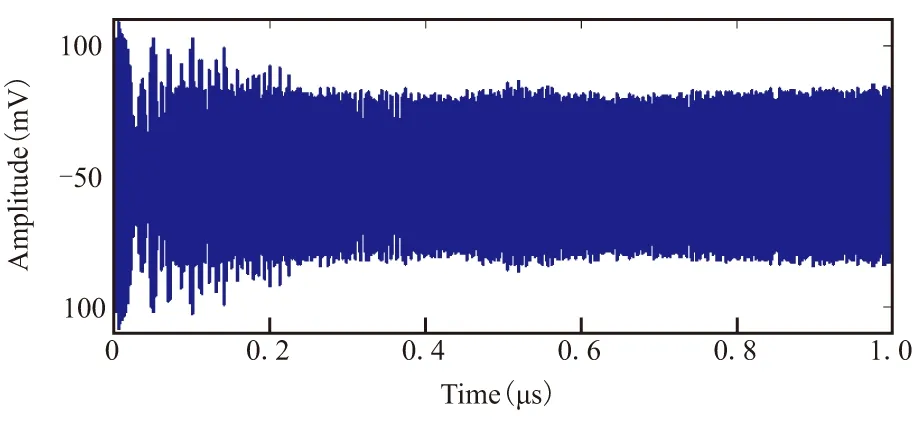
(a)

(b) (c)

在自相关图7(b)中，波形自相关处理后，峰值旁瓣比为6.11 dB；在主瓣放大图中，包络表现出辛格(sinc)函数；时宽为1 μs的双啁啾信号，脉冲压缩后峰值的半高全宽为0.762 ns，对应脉冲压缩比可计算为1312。因此所提方案产生了载频14 GHz、带宽1.6 GHz的双啁啾信号。信号具有好的脉冲压缩性能，更高载频、更大带宽的双啁啾信号可通过改变驱动射频和基带信号获得。

3 信号探测性能分析

3.1 倍频双啁啾LFM信号的模糊函数

为了研究产生信号的探测性能，利用Matlab绘制载频14 GHz、带宽1.6 GHz、时宽1 μs双啁啾LFM信号的模糊函数，如图8(a)所示。可以看出，模糊函数关于原点对称，尖峰位于原点处。因此，除了原点附近外，目标位于其他位置时，雷达都具有精确地位置和速度分辨力。图8(b)为双啁啾信号模糊函数的等值线图。作为对比，图9(a)给出了载频14 GHz、带宽1.6 GHz、时宽1 μs正啁啾LFM信号模糊函数图。可以看出，相比于图9(a)，图9(a)模糊函数表现出“刀刃状”，在刀刃附近存在较大位置-多普勒模糊。而双啁啾信号的模糊函数，刀刃部分降低为1/4，表现出“图钉状”，可以有效提高雷达探测的距离-速度联合分辨力。图9(b)为相同带宽和时宽条件下，单啁啾LFM信号模糊函数的-3 dB等值线。可以看出，所提方案产生的双啁啾信号，-3 dB模糊函数远小于LFM信号。因此，双啁啾LFM信号有效地改善了单啁啾LFM信号存在的位置-多普勒耦合问题，可极大提高雷达系统的探测精度。

(a) (b)

(a) (b)

3.2 倍频双啁啾LFM信号的运动目标探测能力分析

双啁啾LFM信号，模糊函数呈“图钉状”，可以有效解决单啁啾LFM信号存在的距离-多普勒耦合问题。为了验证双啁啾信号的运动目标探测性能，搭建图10的仿真系统。仿真中，利用所提方案产生Ka波段的双啁啾LFM信号，时宽设定为200 μs，中心频率为30 GHz，频率变化范围设定为29.5 GHz-30.5 GHz和30.5 GHz-29.5 GHz。双啁啾信号放大后通过天线辐射到自由空间完成探测。目标与雷达距离设置为24 km，径向速度为0.8 km/s。

图10 双啁啾LFM信号雷达系统运动目标探测示意图

目标回波匹配滤波处理后，输出结果的包络如图11所示。可以看出，图11存在两个匹配滤波峰值，分别对应双啁啾信号的正啁啾扫频信号和负啁啾扫频信号。由于两个单啁啾信号中心频率相同，即对应着相等的多普勒频移，因此目标的真时延应该位于两个匹配滤波峰值的中间，即160 μs，由此可计算目标与雷达的距离为24 km。

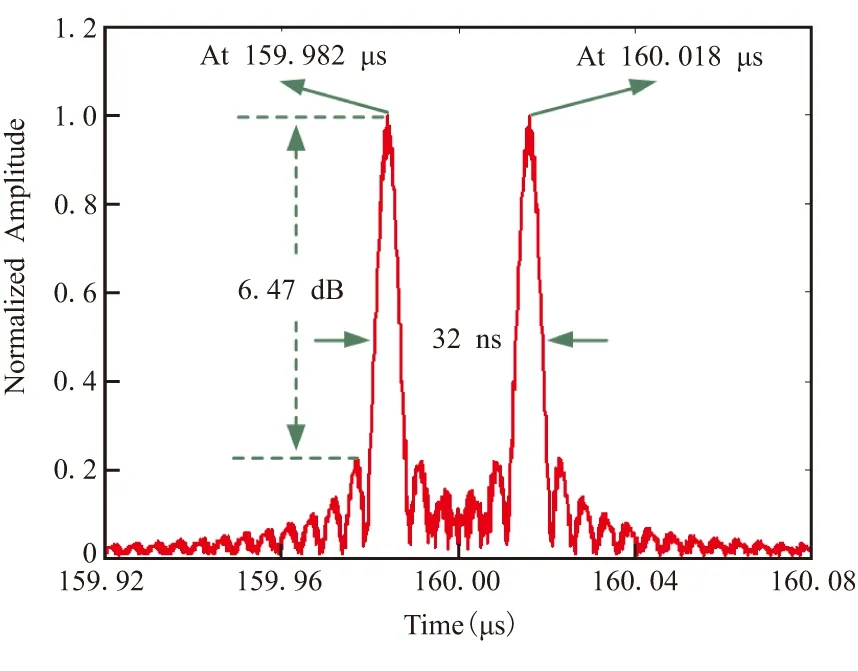
图11 双啁啾LFM信号雷达系统匹配滤波输出结果

目标速度可通过多普勒效应计算，即：

(10)

式中，Δt为啁啾信号波形匹配滤波处理后与真时延的时间偏离，f和B分别为双啁啾信号的载频和带宽，v为目标的径向速度，c为光速，为简化分析取为3×108m/s。在图11中，由于多普勒效应，正负啁啾信号相对于目标真时延分别偏离了-18 ns和+18 ns，带入式(6.20)中，可计算得到目标的径向速度为0.8 km/s。由此可知，雷达观测场景中，目标相对于雷达距离为24 km，速度为0.8 km/s，与仿真设置相同。此外，当雷达分别使用正啁啾信号和负啁啾信号观测目标时，匹配滤波结果将存在-2.7 m和+2.7 m的位置误差，且无法测量到目标的速度信息。

雷达工作在单啁啾LFM信号体制下，当发射信号脉冲比较窄、啁啾率比较低、观测目标径向速度不太高时，LFM信号具有多普勒频移不敏感的优势。但处于空间运动状态的观测目标速度一般都比较快，如弹道导弹再入大气层时速度可达5000 m/s以上，四代战机也具备超音速巡航的能力，此时LFM信号的多普勒-时延耦合现象将导致雷达一维距离像在时间轴发生平移，出现成像模糊问题。雷达采用双啁啾信号，可有效提高目标探测时的多普勒-时延联合精度，解决单啁啾LFM存在的成像模糊问题。

4 结论

为了产生倍频双啁啾LFM信号，文中提出了一种基于双驱动DP-MZM的方案。理论分析了双啁啾LFM信号的产生原理，利用模数函数研究了双啁啾LFM信号对雷达探测性能的改善。实验产生了载频14 GHz、带宽1.6 GHz、时宽带宽积1600的双啁啾LFM信号。对信号的波形进行自相关处理，峰值旁瓣比为6.11 dB，1 μs的波形被压缩至0.762 ns，对应脉冲压缩比为1312。所提方案无需偏振器件和光滤波器，具有操作简单、调谐性高的优势，产生信号表现出好的旁瓣抑制性能和脉冲压缩性能。最后，分析了产生信号的探测性能，双啁啾LFM信号模糊函数呈近似“图钉状”，表现出好的位置-多普勒联合分辨力；在运动目标场景中，所提方案产生的信号可准确探测到目标的速度和位置信息，而单啁啾信号由于位置-多普勒耦合问题，将存在2.7m的测距误差。