稀疏表示模型及高光谱遥感应用研究

张敬尊，张睿哲，徐光美，王金华，何 宁

(北京联合大学 智慧城市学院，北京 100101)

0 引 言

稀疏表示作为一种新型的数据挖掘技术，具有严谨的理论支撑和多领域的应用验证，近年来成为机器学习、模式识别、图像处理等领域的研究热点。相较于传统算法，稀疏表示类算法更善于发现隐藏在数据背后的知识，具有优秀的特征发现和保持能力，同时对于图像中的噪声具有鲁棒性，受噪声干扰小。该理论认为自然信号可以表示为原子信号的稀疏线性组合，基于特定的基元(Basis)或字典(Dictionary)，信号(X)可以通过少量系数进行紧致表示。由于多学科的研究背景，不同领域对稀疏表示的研究各有侧重，由此引申出的模型表征也各不相同，自成体系，不利于多领域的应用拓展。遥感领域具有数据密集、计算密集的特点，其应用需求与稀疏模型优势相吻合，但由于上述局限，稀疏模型在遥感领域的引入不足，应用受限。

鉴于上述分析，该文对统计学、信号处理、计算机视觉和机器学习等领域中对稀疏表示的研究进行了调研，以遥感应用需求为导向，提出了遥感适用的稀疏表示框架，基于遥感领域应用不足的现状，着眼于高光谱图稀疏处理，归纳了现有的研究基础及面临的问题，以期为稀疏模型遥感应用的进一步深入提供参考。

1 稀疏表示的多领域研究基础及应用

稀疏表示起源于生物视觉领域，1959年Hubel和Wiesel两位生物学家在研究猫的视觉条纹皮层上细胞的感受野时首次提出了“稀疏”概念，二人在论文中指出“初级视觉皮层(即V1区)上的细胞的感受野能够对视觉感知信息产生一种稀疏的响应，即大部分神经元处于静息状态，只有少数的神经元处于刺激状态”[1]。之后，Barlow等人于1972年给出了“稀疏性和自然环境的统计特性之间存在着某种相关性联系”的推论[2]。利用该推论，Olshausen和Field于1996年提出了稀疏编码，验证了自然图像经过稀疏编码后，学习得到的基函数可以近似描述V1区上简单细胞的感受野的响应特性[3]。两位科学家于1997年又引入了过完备基(又称为字典)，并提出了基于过完备基的稀疏编码算法[4]。

在数学领域尤其是统计学领域，法国数学家Mallat于1993年基于小波分析提出“信号可以用一个过完备的字典进行表示”，继而开创了该领域稀疏表示的先河[5]。随后，Rudin[6]、Tibshirani[7]等人围绕l1范数对稀疏性应用进行了理论深入研究。Donoho和Elad于2003年证明只要稀疏界限得到满足，基于通用字典的稀疏表示唯一解可以通过l1范数最小化方法获取[8]。Candes就信号的稀疏性和l1范数的关系给出了明确的定理[9]，随后，Donoho[10]及Baraniuk[11]等提出了压缩感知(Compressive Sensing)的概念，从信号表达的角度证明了稀疏表达是高维信号(如音频、视频等)在特定基向量(如傅里叶基、小波基等)或者字典(Dictionary)上的一种自然表达，由此发展的约束化优化求解策略为信号的稀疏表达提供了近似最优的可计算模型。针对转换后的l1范数优化问题，斯坦福大学的Tibshirani教授提出了经典了最小绝对收缩和选择算法LASSO(Least Absolute Shrinkage and Selection Operator)[12]，此后，很多学者又在此基础上进行了深入研究，并提出了Adaptive Lasso[13]，Fused Lasso[14]等基于LASSO算法的变体。

机器学习领域优化理论的发展为稀疏问题求解提供了强有力的技术支撑，稀疏表示转化为基于不同范数约束的目标函数最优化问题，在自然图像处理、人脸识别等子领域中均有非常成功的应用。就稀疏编码问题，发展出了匹配追踪算法(Matching Pursuit，MP)[5]和正交匹配追踪算法(Orthogonal Matching Pursuit，OMP)[15]两个经典求解算法；针对字典学习问题，Engan等人提出了MOD算法(Method of Directions)[16]，Aharon等人提出了经典的K-SVD算法[17]，Mairal等人提出了线上字典学习算法[18]。

伴随统计学领域理论研究的深入，稀疏表示模型在信号处理、计算机视觉、图像处理等多个领域取得了很多成功的应用，总结各领域的研究分支如表1所示。

表1 稀疏表示模型领域应用总结

由于多学科的研究背景，稀疏表示在不同的领域各有研究侧重，由此引申出的关键词/术语描述也略有不同，主要包括：稀疏表示(Sparse Representation)、稀疏表达建模(Sparse Representation Modeling)、稀疏建模(Sparse Modeling)、稀疏机器学习(Sparse Machine Learning)、稀疏启发模型(Sparse-inspired Model)、稀疏优化(Sparse Optimization)、稀疏估计(Sparse Approximation)、字典学习(Dictionary Learning)、稀疏编码(Sparse Coding)、稀疏分解(Sparse Decomposition)。综合各关键词的表达侧重，基于该文的研究背景和遥感应用领域，采用关键词稀疏表示(Sparse Representation)用以描述挖掘数据稀疏性的整体框架，字典学习(Dictionary Learning)和稀疏编码(Sparse Coding)是其中的两个主要任务。

2 数学模型

稀疏表示的核心是信号拟合问题，对于复杂的多维信号来说，将每个信号看作为由多个基函数(基变换)的线性组合，且其中大部分基函数对应的系数为零，每个基函数被称为基元(Basis)，所有基元的组合为字典(Dictionary)，信号基于字典的系数是稀疏的。已知字典，求解信号的最优稀疏分解系数或稀疏逼近过程称为稀疏编码(Sparse Coding)，基于信号寻求其低维最优字典的过程称为字典学习(Dictionary Learning)。

2.1 稀疏编码

已知信号集X=[x1,x2,…,xn]∈Rm×n，基于字典D=[d1,d2,…,dk]∈Rm×k，稀疏编码的目标是从字典中找到最小的基元子集对每个信号xi∈Rm进行无噪声数据的精确表示。

(1)

或含噪声数据的近似表达：

(2)

上式等价于：

(3)

(1)l0范数，非零元素的个数，‖α‖0={i:αi≠0}。

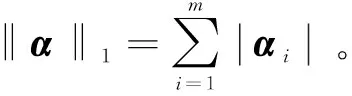
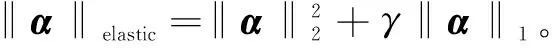
(4)lr,p范数，‖A‖r,p=‖(‖A1‖r,…,‖Am‖r)‖p,A∈Rm×n。

其中，(1)～(3)三种诱导函数适用于各信号间相互独立的情况，(4)用以刻画信号间的结构关系，即信号间彼此不独立，如图像分类问题中通常假设相邻像元属于同一类别，即相邻元素的稀疏表达关联相同组合的字典基元，由此，相邻像元的多个系数向量可构成行稀疏矩阵。有学者[19]在特征选择的具体应用中将其称为Vector-based和Matrix-based。实际应用领域的降维、分类、去噪、目标识别等子问题均可看作是上述模型的具体体现，不同应用背景及领域先验知识前提下，损失函数有其针对性体现和扩展，通过不同的稀疏诱导函数以获得问题的最优解。针对由不同稀疏诱导函数构建的稀疏编码模型，统计学、信号处理、机器学习等领域的学者提出了诸多优化求解算法[20]。依据稀疏诱导函数类型，对应的稀疏模型和经典求解算法如下：

基于l0范数对应的数学模型为：

(4)

或

(5)

基于l0范数的稀疏编码模型是对数据稀疏性的简单而直观的描述，实际应用中，由于其非凸性使得目标函数的求解为NP难题，其求解多采用贪婪类算法，即首先确定解向量的支持集，然后直接利用最小二乘优化在支持集上求解稀疏系数α。典型代表算法包括匹配追踪算法MP[5]和正交匹配追踪算法OMP[15]。

2.2 字典及字典学习

字典是稀疏表示模型性能的制约因素，通常，根据字典基元的构建方式一般可将字典分为预定义字典、自适应字典和学习字典三类。

预定义字典是稀疏表示中最初的字典形式，通常称为过完备字典，即字典中基元的个数超过信号的维数，在过完备字典前提下，任一信号在不同的基元组下都有不同的稀疏表示。过完备字典通过已知的变换基进行选取，如傅里叶、离散余弦或小波等[21]，一旦完成构建则字典保持固定不变且将用于表示所有的信号。这种方法相对简单易实施，对特定类型的信号非常有效，而对于其他类型的信号表示效果则可能非常不好。

自适应字典在预定义字典的基础上通过在特定参数(连续或者离散的)控制下生成字典基元[22]，其应用的泛化能力具有明显的局限性。

无论是预定义字典还是自适应字典通常都具有较快的变换速度，但两种字典都不能处理稀疏信号，且其仅适用于特定类型的图像和信号，无法用于新数据。针对上述缺点，Olshausen和Field两位生物学家摒弃传统的基于理论的字典构建方式[3]，从训练样本中发掘数据中隐藏的知识，并抽取为字典基元，继多次开拓性实验后，二人证明了这种方式获取的字典可以很容易地发现自然图像中的底层结构，该研究可以看作是学习字典的起源，之后，在此基础上逐渐展开了更为深入的研究。

学习字典引入了学习机制，其字典基元通过训练和学习大量的与目标信号相似的数据来获得，其构建过程是动态的，学习所得字典能够适用于符合稀疏定义的任何类型的信号。基于已知信号构造字典的过程称为字典学习，构造的字典可以对指定信号进行稀疏表示是基本前提，因此，信号的最优稀疏表示是字典学习的目标。从待表示的数据出发，字典学习算法寻求与待表示数据相关且完备的字典基元，该类方法通过学习样本可以保持与实际应用的高相关性[23]，具有灵活性大，表示性能好等优点，但同时该类方法计算量大，需要根据具体的任务进行学习[20]。

字典学习问题数学模型如下，已知训练样本X=[x1,x2,…,xn]∈Rm×n，基于一定的先验知识约束，寻求最优字典D，以使得样本集中每个信号在D上具有最优稀疏表达。

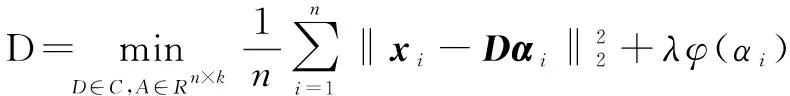
(6)

其中，A=[α1,α2,…,αn]∈Rk×n包含了训练样本的稀疏系数X=[x1,x2,…,xn]，φ:Rk→R是稀疏诱导函数，用以控制系数稀疏度，实际应用中有各种体现形式，λ为调节参数，平衡系数稀疏性和模型拟合度，通常情况下，λ值越大，则系数中非零元素越少，但二者之间并非单调递减关系，相关研究有待深入。C包含了对字典的限制，通常采用如下形式：C={D∈Rm×k|∀j‖dj‖2≤1}，即将字典D各列元素的值限制在一个l2-ball范围内，以防止其过大或过小而导致系数向量αi各元素值波动剧烈。

与稀疏编码问题类似，从其他描述角度模型式(6)还有如下三种形式：

(1)约束形式变体形式：

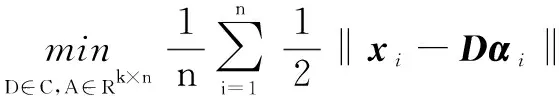
s.t.φ(αi)≤μ

(7)

等价于，

(8)

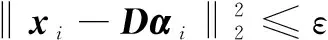
(2)矩阵分解角度变体形式：

(9)

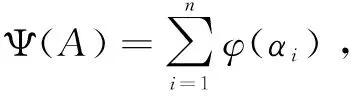
(3)经验风险最小化变体形式：

(10)

其中，L:Rm←Rm×n为如下形式损失函数：

(11)

此时，字典学习问题转换为经验风险最小求解问题。部分实际应用中，人们并不关心经验函数fn(D)的准确最小值，而是更以其期望最小f(D)为目标，以此来衡量学习到的字典在新数据上的有效性。

(12)

字典学习算法通常给字典设定初值，然后基于稀疏表示的结果对字典基元进行更新，算法包括基于字典的样本表示、字典基元更新两个主要阶段，其中样本表示阶段与上节的稀疏编码相对应，文中总结的算法均可以用于该阶段的问题求解，字典构建阶段以训练样本为输入，学习字典为输出。以应用背景为前提的数学模型构建、编码策略选择、字典构造方案设计是字典学习的三个关键问题。经典的字典学习算法包括最优方向算法MOD[16]、K-SVD算法[17]，两种算法在许多领域中得到了应用，特别是在图像和音频处理方面。

3 稀疏表示模型高光谱遥感图像应用

Elad等人证明了图像的稀疏性[24]，自此，稀疏模型成为图像处理领域的研究热点。遥感图像由于成像机理复杂、数据量大等特点，稀疏模型的应用相对较少。高光谱遥感图像作为一种典型的超高维数据，具有谱间高相关性以及地物空间分布排列的稀疏性特点，面临如何从海量高维数据中挖掘出感兴趣地物诊断性信息的瓶颈。稀疏表示则恰好可以针对上述高相关所致的高冗余与感兴趣信号的稀疏性进行地物信息的有效分析，突破瓶颈，因此，在高光谱图像的降维[25]、去噪[26]、解混[27]、分类[28]以及目标探测[29]等任务中均有稀疏模型的应用研究。该文重点对稀疏降维和稀疏分类展开分析。

有学者研究发现，在不影响解译精度的前提下，90%的光谱波段是冗余的[30]，在保证解译性能的前提下发现更具判别性的特征是高光谱降维任务的目标，不仅可以提高地物分类和探测的效果，同时也可以降低数据处理的复杂度，提高计算效率。特征选择类降维方法从原始波段空间选择更具表征性的子集，相对于原始冗余的光谱波段信息而言，目标波段子集是稀疏的，设定合理的目标函数以便于尽量多地保留原始数据的主要光谱特征，算法本质上是组合优化问题。该类方法可以有效保证光谱波段的物理意义，但尽量“多”的特征与尽量“少”的冗余两个目标之间是相互制约的，目前国内外研究较少[31]。特征提取类算法首先将原始的高光谱特征进行映射，之后在映射后的特征中进行分量选择。有学者研究了组稀疏逐层变换进行高光谱降维[32]，此外稀疏保持投影算法SPP(Sparse Preservation Projection)在高光谱降维中研究也较集中[33]，但上述方法均需利用已知的样本信息作为先验，利用稀疏模型寻求高维信号在低维子空间的映射，算法属于监督降维，样本标记代价高。近期，有学者开展半监督稀疏降维[25]，削弱了模型对训练样本的依赖。利用稀疏性驱动进行高光谱图像维数约简研究，已经成为业内的研究热点问题，非监督类稀疏降维以及算法时空复杂度的进一步降低亦有待开拓性研究。

另一方面，基于稀疏表达的高光谱图像分类也越来越受到关注，针对高光谱数据冗余性，将高维信息表达为稀疏字典与其系数的线性组合，采用稀疏表达对高光谱图像进行处理，能够简化分类模型中参数估计的病态问题[34]，可以看作稀疏模型用于高光谱图像分类任务的开创性研究，论文中选取所有的训练集作为字典并基于该字典对所有待分类像元进行稀疏表达，同时通过邻域空间拉普拉斯算子对相邻像元间的空间关系进行刻画并对稀疏表达的结果作后验修正。其实验结果表明，基于稀疏表达的算法相较于其他传统算法性能有明显提升，不足之处在于存在过平滑现象，同时，算法中使用的字典为预设的固定字典，未对训练集数据的特征保持度、训练集数量敏感度作针对性学习。此后，为缓解过平滑现象，有学者将非局部空间相关性[35]，结构形状先验[36]对稀疏表示模型进行扩展，此外，还有学者将核化算法引入到稀疏表示模型中用以求解高光谱信号的非线性可分问题[37]。基于稀疏表示的高光谱图像分类成为高光谱领域的另一研究热点，受制于高光谱图像中同物异谱、异物同谱现象严重，地物分布复杂，空间尺度差异大，有标记样本少，噪声类型复杂多样等情况，当前的图像分类研究仅能同时应对其中的部分问题，还难以自动化完成大面积地物识别的任务[38]。同时，为充分发挥稀疏表示模型的优势，相较于上述研究中所使用的固定字典而言，基于训练集的字典学习研究也成为必然需求。

综上，作为一种典型的超高维数据，高光谱信号处理面临如何从海量高维数据中挖掘出感兴趣地物诊断性信息的瓶颈。传统图像处理平台和信息提取方式在面对体量巨大的高维原始数据时难以满足目标信息快速获取的需求。稀疏学习可以利用海量高维数据的高冗余性与感兴趣信号的稀疏性，能够有效提取出高光谱地物信息，该技术在高光谱图像的恢复、重建以及分析等任务中的应用研究逐渐开展，但相对于机器学习、计算机视觉等领域而言，高光谱领域的应用在深度上有待进一步深入，仍存在较大的研究难点和潜力[39]，具体如下：

(1)最优稀疏学习方法或模式的选择非常困难，解决问题的角度选取以及恰当的稀疏诱导函数选择都没有标准可以参照。

(2)学习字典相对于固定字典的优势明显，但尽管各领域对于字典学习已有较为详细的研究及成果，但在具体应用时需要结合应用背景进行针对性模型构建，模型中先验知识的刻画以及字典基元数量与学习过程中的数值计算，内存消耗以及与信号表达的有效性之间的关系均需作针对性的分析。

(3)结合高光谱遥感图像独有的特性，对图像的上下文、形态特征等先验知识进行合理刻画并与稀疏表示框架结合，将稠密数据转为稀疏数据，从而提升算法性能仍有很多问题需要解决。

(4)海量数据下，样本标记代价非常高，亟需无监督类稀疏模型的开拓性研究。

(5)当处理高维遥感数据时，所需的训练样本量和相应的计算负荷增加，同时兼顾算法的性能和速度面临挑战，亟需高性能解决方案。

4 结束语

稀疏表示的本质是用尽可能少的资源表示尽可能多的知识，这种表示方法的有利之处在于既可以节约数据的存储空间，又能提高计算速度。伴随稀疏表示在高光谱图像处理领域应用的逐渐深入，稀疏表示框架的优势逐渐被认知和推崇，除高光谱外其他类遥感图像处理任务中对该框架的引入以及适用性亦有待进一步探究。同时，在大数据量背景下，在保证图像处理算法性能的同时，进一步降低算法的空间占用和计算复杂度，基于高性能的遥感数字图像处理亦成为当前及未来遥感应用的迫切需求。