双目标用户均衡下的交通流逐日动态演化模型 ①
徐 薇, 马箫宇, 徐红利
(南京大学工程管理学院, 南京 210093)
0 引 言
自1952年Wardrop提出用户均衡(user equilibrium, UE)概念开始,关于交通网络均衡分配的研究就一直在不断发展深入,推动着交通科学的发展.静态交通分配模型通常只关注交通系统平衡稳定的最终状态,而动态交通分配模型则刻画交通流从非平衡状态到平衡状态的演化过程.现实中,由于出行者每天的出行选择都可能会受到过往出行经验和当前网络状态的影响而发生改变,因此交通流的分布状态是振荡变化的.对交通流逐日动态(day-to-day dynamics)演化过程的研究有利于探索交通流演变的内在机制,更好地实现交通诱导和对交通网络流状态的控制.
在现有的交通流逐日动态演化研究中,大多数模型假设出行者根据前一天的道路通行时间来选择当天的出行路径,从而将相邻两天同一路径/路段上的流量更新描述为当天路网状态(如路径/路段通行时间)的一个函数.现有文献中基于路径流量更新的模型较多,Yang和Zhang[1]总结了五类模型,分别是:the simplex gravity flow dynamics[2], the proportional-switch adjustment process (PSAP)[3], the network tatonnement process[4], the projected dynamical system[5], 以及the evolutionary traffic dynamics[6].这些模型都假设系统的最终稳定状态是确定的UE.在此基础上,很多学者进行了拓展研究,例如考虑:有限理性[7, 8]、参考点依赖[9]、弹性需求[10]、随机用户均衡[11, 12]、混合均衡[13]、路径成本敏感性[14]、路径剩余容量[15]、诱导信息[16, 17]、社会交互[18]、交通事件影响[19]等.由于路径流量不易观测且存在路径重叠和枚举量大的问题,He等[20]最早提出了直接基于路段流量更新的逐日动态演化模型.Han和Du[21]进一步研究了该模型的一些性质,如不变集和限制稳定性.Guo等[22, 23]给出了一种基于路段的逐日动态演化的一般框架,并且证明了一些已有模型(例如文献[4, 5, 20, 21]提出的模型)均为该一般框架的特例.此外,在基于路段的模型中,也有学者考虑了出行时间不确定性和出行者风险行为[24]、道路容量退化[25]等.Xiao等[26]还将逐日交通网络动态演化过程看作是一种物理系统,探究了其中的内在规律.
道路收费是交通诱导和控制的一种重要手段,在交通流逐日动态分配模型的研究中有不少引入了道路收费策略,例如Tan等[27]、Guo等[28]、Han等[29]、Liu等[30]、Xu等[31]、Rambha和Boyles[32]等.这些研究均假设出行者将道路通行时间与收费组合为广义出行成本来考虑路径选择,即最小化广义出行成本.然而,将道路出行时间和收费组合考虑会使二者之间具有某种潜在的转换与互补关系.Dial[33]较早考虑多目标交通配流问题时就将两者进行了线性组合,而近来Wang和Ehrgott[34]则真正将道路通行时间和收费分开考虑,定义了双目标用户均衡(bi-objective UE,BUE),即达到均衡时出行者无法通过单方面改变路径选择来降低其出行时间或收费.若出行者是理性的,则可以证明达到BUE时任何被使用的路径都是占优路径(也称有效路径),这些有效路径包含了Dial[33]在其研究中定义的所有有效路径,因此BUE更具有一般性.然而,已有的同时考虑道路通行时间和收费的交通流逐日动态演化模型最终均收敛至广义出行成本下的单目标用户均衡,尚无研究对上述双目标用户均衡给出交通流的动态演化过程.因此,本文提出一种新的基于路径流量更新的逐日动态演化模型,假设出行者在逐日的路径选择中将路径出行时间和收费分开比较以决定是否变换路径,可以证明该演化模型最终收敛的稳定状态恰好是BUE.本文严格证明了模型的收敛性,并用数值算例验证了模型的有效性.
1 模 型
1.1 符号定义和假设
考虑一个具有N个节点,L条直接相连的路段构成的交通网络G(N,L).令W是网络中所有OD对的集合,Pw是连接OD对w∈W的所有路径的集合.本文研究假设所有OD对之间的出行需求是固定的,表示为向量d=(dw,w∈W)T,其中dw为OD对w∈W之间的出行需求.路径流量表示为向量f=(fp,w,p∈Pw,w∈W)T, 其中fp,w是路径p∈Pw上的流量.路段流量表示为向量x=(xa,a∈L)T,其中xa是路段a∈L上的流量.令Δ=(δa,p,a∈L,p∈Pw,w∈W)表示路段-路径关联矩阵,其中δa,p=1表示路段a位于路径p上;否则,δa,p=0.显然,x=Δf.令Θ=(θp,w,p∈Pw,w∈W)表示OD-路径关联矩阵,其中θp,w=1表示路径p连接OD对w;否则,θp,w=0.显然,d=Θf.因此,可行路段流量和路径流量的集合为Ω={(x,f)|x=Δf,d=Θf,f≥0}.
本文考虑可分的路段出行时间函数,即路段a上的通行时间只与该路段上的流量xa相关,与其他路段的流量无关.并且假设该函数连续可微,关于路段流量xa严格递增.另外,假设路段收费与流量无关.用ma和ta分别表示路段a上的收费和通行时间,mp和tp分别表示路径p上的收费和通行时间.
1.2 双目标用户均衡(BUE)
本文同时考虑时间和费用两个属性下的出行者路径选择行为,在双目标用户均衡下,出行者总是尽可能地选择通行时间短并且通行费用低的路径[33].文献[33, 34]中给出了BUE的严格定义,为参考方便这里复述如下.
定义1当交通网络流量分布达到BUE时,所有被使用的路径都是有效的.
定义2令f∈Ω是一个可行路径流量分布,mp(f)和tp(f)分别为路径p∈Pw上的收费和通行时间,则
1)如果不存在路径p′∈Pw,满足mp′(f)≤mp(f)和tp′(f)≤tp(f)中至少有一个不等式是严格不等式,则路径p∈Pw是有效的.
2)如果mp′(f)≤mp(f)和tp′(f)≤tp(f)中至少有一个不等式是严格不等式,则路径p′占优路径p,且成本向量(tp′(f),mp′(f))占优(tp(f),mp(f)).
显然,由定义2可知,一条路径是有效的当且仅当这条路径不被其他的任何路径占优.
1.3 逐日动态演化模型
经典的逐日动态演化模型——PSAP模型由Smith[3]提出,该模型描述了在出行时间较长的路径上的出行者会在下一天转移到其他的出行时间较短的路径上,且转换的比率是和该路径与其他较短时间路径的时间成本差成比例的.假设在一个OD对中,p和q分别表示该OD对w∈W之间的不同路径,则路径p上的流量变化率定义为
fp[tp(f)-tq(f)]+)
其中 [x]+=max{0,x}.
上述模型是基于连续时间的,文献[20]中则提到了PSAP的离散形式,具体如下
fp(n+1)-fp(n)=
fp(n)[tp(n)-tq(n)]+)

这里Tw(n)可以视为一个离散化的步长;M是一个参数,在取值较大时意味着出行者更愿意保持原来的路线.
以上是基于传统单目标UE的逐日动态演化模型.本文从双目标用户均衡的路径选择决策规则出发,依据PSAP的思想,对相邻两天路径流量的变化调整给出了如下的定义.
定义3基于双目标用户均衡的逐日动态演化模型定义为
fp(n+1)-fp(n)=
[mq-mp]+-fp(n)[tp(n)-tq(n)]+*
[mp-mq]+)
(1)
其中运算符“*”定义为
并且
[mp-mq]+}+1
这里Tw(n)可以保证fp(n+1)非负,且作为分母不为零;λ(n)∈(0,1]是调整系数,在现实中,它代表愿意调整路径的出行者所占的比例.λ(n)取值越小,表示有调整路径意愿的出行者越少,即更多的人愿意保持原来的出行路径.后文会详细讨论λ(n)的取值.由运算符“*”的定义,式(1)表示只有当路径的时间成本和金钱成本均不增加且至少有一个减少时,出行者才可能改变路径选择,符合BUE下的路径选择决策规则.
2 稳定点和收敛性分析
2.1 稳定点与BUE解的等价性
文献[34]的研究已经表明,BUE解不唯一,令BUE的解集集合为B.
定理1如果路径流量分布f(n)是演化模型(1)的稳定点,则f(n)是BUE解,即f(n)∈B.
证明显然,演化模型(1)的稳定点满足
[tp-tq]+*[mp-mq]+=0,
∀fp,fq>0,p,q∈Pw
因此要证明稳定点f(n)是BUE解,即需要证明所有流量大于零(fp(n)>0)的路径是有效路径.
采用反证法假设存在流量大于零的路径p不是有效路径,即存在路径p′占优路径p,那么由定义2可得,tp′(n)≤tp(n)和mp′≤mp成立,且至少有一个是严格不等式.那么,[tp(n)-tp′(n)]+*[mp-mp′]+>0,此时f(n+1)≠f(n),即f(n)不是稳定点,与假设矛盾.因此,如果f(n)是稳定点,则f(n)∈B.
2.2 演化模型的收敛性
考虑文献[34]中的优化问题(23),具体如下
fp≥0,∀p∈Pw
(2)
其中g∶R→R是关于收费的严格递增函数,由时间和金钱的无差异曲线决定.无差异曲线(indifference curve)是经济学中的一个概念,它是一条表示给消费者相同满足程度的商品组合的曲线.本文研究中的无差异曲线考虑时间和金钱的不同组合,即在同一条无差异曲线上,虽然不同的点表示不同的时间和金钱组合,但是这些点对于出行者来说感受到的效用是相同的.例如,在图1给出的无差异曲线示意图上,假设A点代表出行时间为30 min、收费为20元的路径,B点代表出行时间为60 min、收费为10元的路径,那么对于符合此无差异曲线的出行者来说,路径A和路径B对他们的吸引力是相同的.由文献[34]可知,给定任意一个函数g(即给定任意一个无差异曲线),上述优化问题是一个严格凸优化,其最优解对应的路径流量分布f*是一个BUE解.
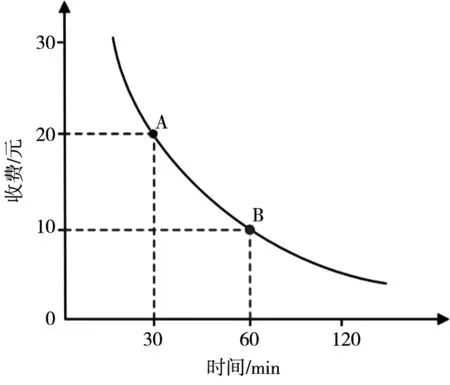
图1 无差异曲线示意图
如果在由定义3给出的逐日动态演化过程中,对任意的n,f(n)∉B,以及任意严格递增函数g,都有W(f(n))>W(f(n+1))成立,那么该演化过程一定会收敛到某个函数g对应的优化问题(2)的最优解,即某个BUE解.因此,接下来将证明存在适当的调整系数λ(n),使得定义3给出的演化过程满足W(f(n))单调下降.
引理1在定义3下,对任意f(n)∉B,总有t(f(n))T(f(n+1)-f(n))≤0,以及mT(f(n+1)-f(n))≤0成立.
(证明见附录)
定理2在定义3下,对任意f(n)∉B,

t(f(n+1))T(f(n+1)-f(n))≤0,

(3)
2)若f(n)满足t(f(n))T(f(n+1)-f(n))=0,则存在λ(n)→0,使得演化模型(1)收敛至BUE状态.
证明令
V(x(n+1))=V(λ(n))
U(f(n+1))=U(λ(n))
则W(f)=V(x)+U(f).
分别对V(λ(n))和U(λ(n))关于λ(n)求导,有
=gTz(n)
其中向量g=(g(mp),p∈Pw,w∈W),z(n)=df(n+1)/dλ(n).由引理1知,对任意的n,f(n)∉B,有t(f(n))T(f(n+1)-f(n))≤0,因此下面分两种情况讨论.
1)若t(f(n))T(f(n+1)-f(n))<0,那么易得t(f(n))Tz(n)<0.于是,当λ(n)=0时
=t(f(n))Tz(n)<0
(4)
由于对每条路段a∈L,ta(xa)连续可微并且关于路段流量xa严格递增,因此对于x∈Ω,t(x)是正定矩阵,即
>0
(5)

=t(f(n+1))Tz(n)
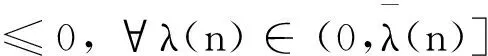
即式(3)成立,并且V(0)>V(λ(n)),即V(x(n))>V(x(n+1)).
另根据引理1,mT(f(n+1)-f(n))≤0,且函数g是关于收费的严格递增函数,因此,gT(f(n+1)-f(n))≤0也成立,即
综上,存在适当的λ(n),使得
即W(f(n))>W(f(n+1))成立.
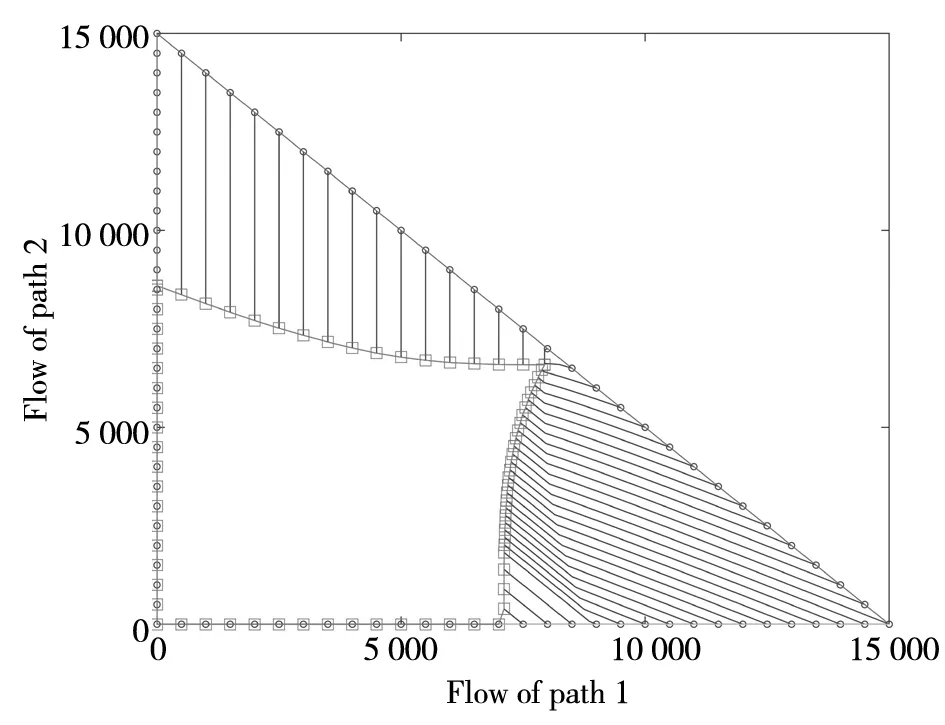
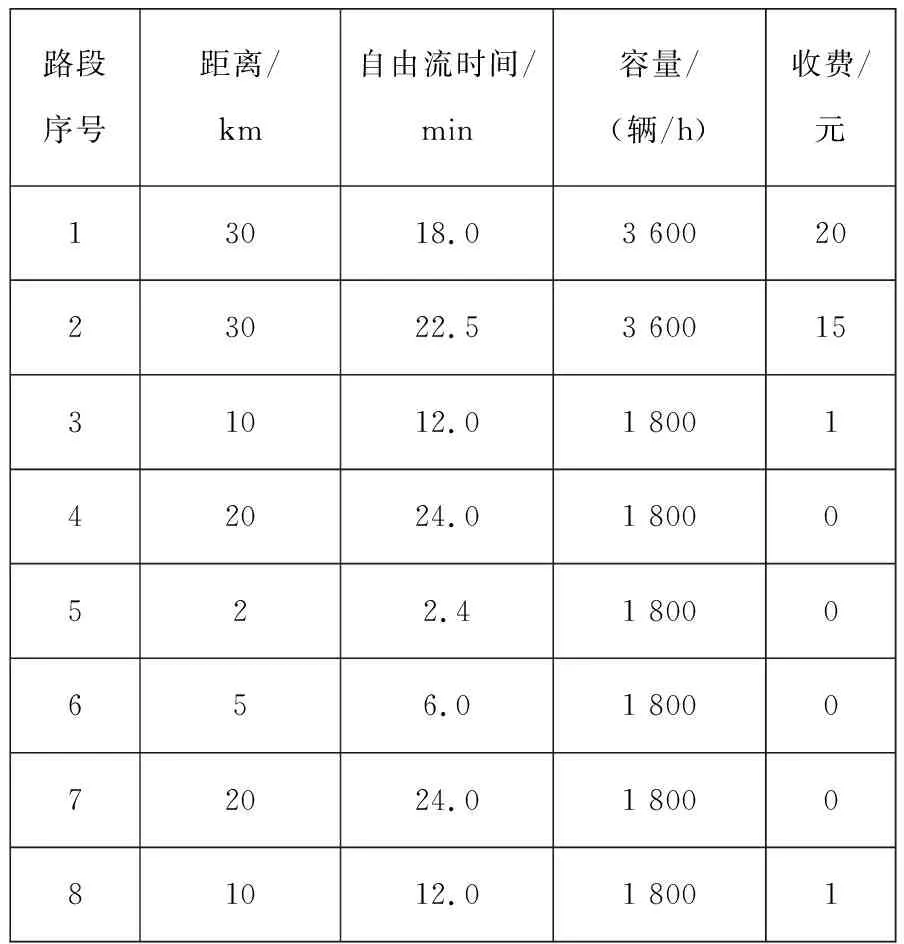
2)若t(f(n))T(f(n+1)-f(n))=0,则由定义3可知,在第n天至第n+1天的变化过程中,人们只是从收费较高的路径调整到了收费更低但时间相同的路径上.即存在路径p,q∈Pw,tp(n)=tq(n),mp>mq,因此部分流量从p调整到q.调整后,有tp(n+1) (6) 注意到该情形下式(6)中的路径i和路径j在第n+1天是不发生流量变化的,因此在第n+2天仍然不会发生变化,因为它们与其他路径的出行时间的大小关系未发生变化,即fi(n+2)=fi(n+1),fj(n+2)=fj(n+1).又因为tp(n+1) 显然,当λ(n)充分小时,式(3)条件一定成立.因此,由上述证明可以直接推出下面的推论1. 推论1在模型假设下,如果λ(n)→0,n=1,2,…,那么演化模型(1)可以收敛至BUE状态. 本节将通过数值算例来检验上节中提出的模型,其中λ(n)的取值会根据推论1和定理2给出的如下两种策略来确定. 策略1调整系数λ(n)取一个趋于0的固定值. 策略2当t(f(n))T(f(n+1)-f(n))=0时,调整系数λ(n)取一个趋于0的固定值;当t(f(n))T(f(n+1)-f(n))<0时,取λ(n)∈(0,1]满足 t(f(n+1))T(f(n+1)-f(n))≤0 以下算例中均采用BPR(bureau of public roads)路段行驶时间函数 图2 算例1网络 表1 算例1网络的路段特征参数 首先,使用策略1,固定取λ=0.001.图3展示了以任意可行流量为初始流量,按照演化模型(1)演化到BUE状态的过程.在图3中,横纵坐标分别为路径1和路径2的流量,圆点为起始点,方点为终止点,从圆点到方点之间的线条表示演化轨迹,方点连线围住的空白区域均为满足BUE的路径流量分布.可以看到,该算例的所有BUE解构成一个集合,未达BUE状态的流量分布会逐渐演化至BUE集合. 图3 使用策略1取λ=0.001时,路径1和路径2上以任意可行流为起点的路径流量演化轨迹 图4展示了使用策略2确定λ(n)取值时的路径流量演化轨迹.同样地,图中圆点为起始点,方点为终止点,星点代表演化过程中的点,方点连线围住的空白区域均为BUE解集.由于策略2是一种自适应策略,因此从任意可行流量开始,只需要迭代相对较少的次数即可演化至BUE状态.和策略1相比,由于每天的调整系数不同,因此演化轨迹相对凌乱无规律. 根据BUE的定义,可推出该算例BUE解析解所满足的条件.表2列出了构成该算例BUE解集的7个子集. 图4 使用策略2确定λ(n)时,路径1和路径2上以任意可行流为起点的路径流量演化轨迹 表2 算例1的BUE解析解 图5展示了表2中7个BUE子集的并集,即整个BUE解集(左下角阴影部分,不含上边界和右边界).这与前面图3和图4中方点连线围住的空白区域是一致的,故进一步验证了演化模型(1)收敛到BUE集合. 图5 算例1的BUE解集 算例1中的交通网络较为简单和特殊,即路段和路径是一样的.下面考虑如图6所示的交通网络[34],该网络具有4个结点、8条路段和6条路径.该网络的路段和路径特征参数分别由表3和表4给出.注意到路径1和路径2是直达路径,路径1是行驶时间最短但收费最多的路径,而路径6是唯一不收费但却最慢的路径.OD对间的出行需求假设为10 000辆车/h. 图7展示了使用策略1,取λ=0.001时,从不同初始可行流开始的流量演化过程.图7(a)的初始流量分布为f= [1 000, 2 000, 3 000, 1 000, 1 500, 1 500],图7(b)的初始流量分布为f=[ 2 700, 1 700, 2 500, 1 000, 800, 1 300].可以看到当初始流量分布不同时,流量的演化过程不同,最终的收敛结果也不同,分别为f*= [1 000, 2 000, 1 997, 1 997, 1 458, 1 548]和f*=[2 700, 1 700, 1 750, 1 750, 800, 1 300].可以验证,这两个最终流量分布都满足BUE条件. 图6 算例2网络 表3 算例2网络的路段特征参数 表4 算例2网络的路径特征参 图8展示了初始流量为f= [1 000, 2 000, 3 000, 1 000, 1 500, 1 500],使用策略2确定λ(n)时的演化过程,此时最终流量为f*=[1 000, 2 000, 1 980, 1 980, 1 435, 1 605],同样容易验证该流量分布中所有被使用的路径均不被其他任何路径占优,因此也是一个BUE解.另外,对比图7(a)和图8可以发现,使用策略2比使用策略1收敛速度快很多. (a) 图8 使用策略2确定λ(n)时的路径流量演化过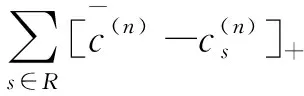
3 数值算例
3.1 算例1






3.2 算例2



4 结束语