一种串联机器人笛卡尔空间轨迹规划方法

郭 领

(南京航空航天大学机电学院，江苏 南京 210016)

对于工业机器人而言，提高工作效率是一个重要目标。在机器人末端执行器沿着固定路径重复执行工作任务的情况下，如何在避免冲击且满足驱动器性能要求的前提下尽可能减少单次任务的执行时间是一个核心问题。该问题的实质是在考虑冲击的前提下沿指定路径的时间最优轨迹规划问题，是机器人运动规划领域的一个分支[1]。

经过几十年的研究，机器人沿指定路径的时间最优轨迹规划问题已经取得了大量研究成果[2]。Bobrow[3]提出了一种通过引入路径坐标来建立参数空间的方法，从而把多维问题转化成二维问题，大大降低了时间最优轨迹规划问题的复杂程度。Pfeiffer和Johanni[4]结合关节转矩的限制条件和轨迹在参数空间的几何性质，提出了一种通过求解转换点寻找最优轨迹的方法。Shiller[5]对轨迹中的奇异点进行针对性处理，提出了一种更加完善的算法。Verscheure等[6]提出一种直接转化的方法，将寻找全局最优轨迹的问题转化为能够直接使用成熟的求解器得到最优解的二阶锥规划问题。Kong等[7]在此基础上使用三次样条曲线在参数空间中对最优轨迹进行拟合，虽然在一定程度上增加了轨迹的执行时间，但得到了更加平滑的轨迹。Reynoso等[8]使用凸松弛方法建立了考虑库仑摩擦力和黏滞摩擦力的机器人完整动力学模型，在此基础上进行轨迹规划。

串联机器人是机器人的一个重要分支，在汽车制造、电子电气、 塑料加工、 机械加工、 化工等行业中有着非常广泛的应用。串联机器人的轨迹规划是串联机器人研究领域的一个重要研究方向，对于提高机器人的工作效率、保证工作环境的安全、提高产品质量以及降低机器人的能量损耗等目标的实现具有重要意义。有鉴于此，本文提出了一种机器人在笛卡尔空间中的无冲击近似时间最优轨迹规划算法。

1 量的书写规则

1.1 基于路径坐标的参数空间建立

轨迹规划时不考虑机器人末端执行器的受力并忽略摩擦力的影响，机器人的动力学方程为：

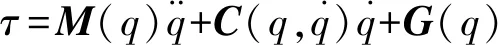
(1)

运用文献[3]的方法引入路径坐标s，可建立q与s之间的函数关系如下：

(2)

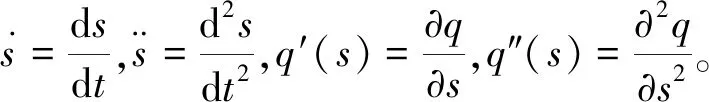
(3)

其中：

m(s)=M(q(s))q′(s)

(4)

c(s)=M(q(s))q″(s)+C(q(s),q′(s))q′(s)

(5)

以机器人轨迹规划执行时间T作为目标函数，根据式(2)可得：

(6)

由此机器人时间最优轨迹规划问题可描述为:

(7)

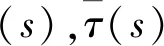
1.2 轨迹规划问题转化为二阶锥规划问题

二阶锥规划属于凸优化的一个分支，现有算法和常规计算能力已足以可靠地求解大规模凸优化问题。二阶锥规划的标准形式为：

(8)

将式(7)中的目标函数及约束条件转化成二阶锥规划标准形式的过程包括以下几个步骤。

(9)

从而可以将式(7)转化为：

(10)

第二步：离散化。首先将路径坐标离散成(K+1)个点：s0=0≤sk≤1=sK，k=0,…,K；然后在每个离散点取bk=b(sk)，其中：bk为b(s)在第k个离散点的函数值；sk为第k个离散点的横坐标。

将曲线b(s)在区间[sk,sk+1]视为直线，则有：

(11)

从而可以将式(10)(目标函数)的右半部分转化为：

(12)

(13)

第三步：转化成二阶锥规划问题。首先引入变量ck和dk，限制条件为：

(14)

(15)

从而有：

(16)

由式(14)和式(15)得：

(17)

(18)

综上所述，最终得到的转化成二阶锥规划形式的时间最优轨迹规划问题如下：

(19)

2 消除冲击的轨迹规划算法

求解式(19)中的二阶锥规划问题，可以得到满足约束条件且执行时间最短的轨迹。但由于时间最优轨迹规划问题中并未对转矩随时间的变化率进行约束，因此在某些点会存在转矩变化率过大的问题，即机器人末端执行时间最优轨迹时存在冲击。因此，本文在完成二阶锥规划求解出机器人末端执行器时间最优轨迹之后提出一种无冲击近似时间最优轨迹规划算法，算法流程图如图1所示。

图1 消除冲击的算法流程图

首先运用文献[3]的方法建立参数空间，并将机器人关节输出转矩约束条件转化为参数空间的约束条件；然后将轨迹规划问题转化成二阶锥规划的形式并使用求解器求出全局最优解，此解为没有考虑转矩变化率的时间最优轨迹，因此存在冲击。为消除冲击，首先计算出机器人各关节转矩，建立描述冲击情况的轨迹冲击函数，并求出所有路径点的冲击函数值；然后设置冲击点的筛选条件，从而得到原轨迹上冲击点及其路径坐标值。针对每个冲击点，在参数空间中使用五次多项式对冲击点所在优化区间内的轨迹进行局部优化处理，从而消除冲击。处理完所有冲击点后，考虑到使用五次多项式处理时对原轨迹的改动可能导致新的冲击点的产生，因此重新计算轨迹冲击函数值并判断是否存在冲击点；若依然存在冲击点，则在确定新冲击点路径坐标之后重复之前对冲击点进行局部处理的步骤，并一直循环，直到轨迹中不再存在冲击点，最终得到无冲击轨迹。

求解式(19)中的二阶锥规划问题后，根据其中τk的表达式可计算出时间最优轨迹所有路径点处各关节的转矩值，本文将转矩变化率的绝对值定义为冲击，为描述冲击变化情况，构造冲击函数如下：

(20)

其中：

在得到轨迹上所有路径点处的冲击函数值之后，需要设置一定的条件来筛选出冲击点。本文将筛选的阈值设置为最大冲击函数值的1/M，将冲击函数值大于此阈值的点作为冲击点，M值可根据对轨迹的要求进行适当的调整。通过筛选得到冲击点后，根据其路径坐标在b(s)曲线上找到对应点，并使用五次多项式对b(s)曲线上冲击点所在的优化区间进行局部处理。局部优化处理的操作流程如图2所示。

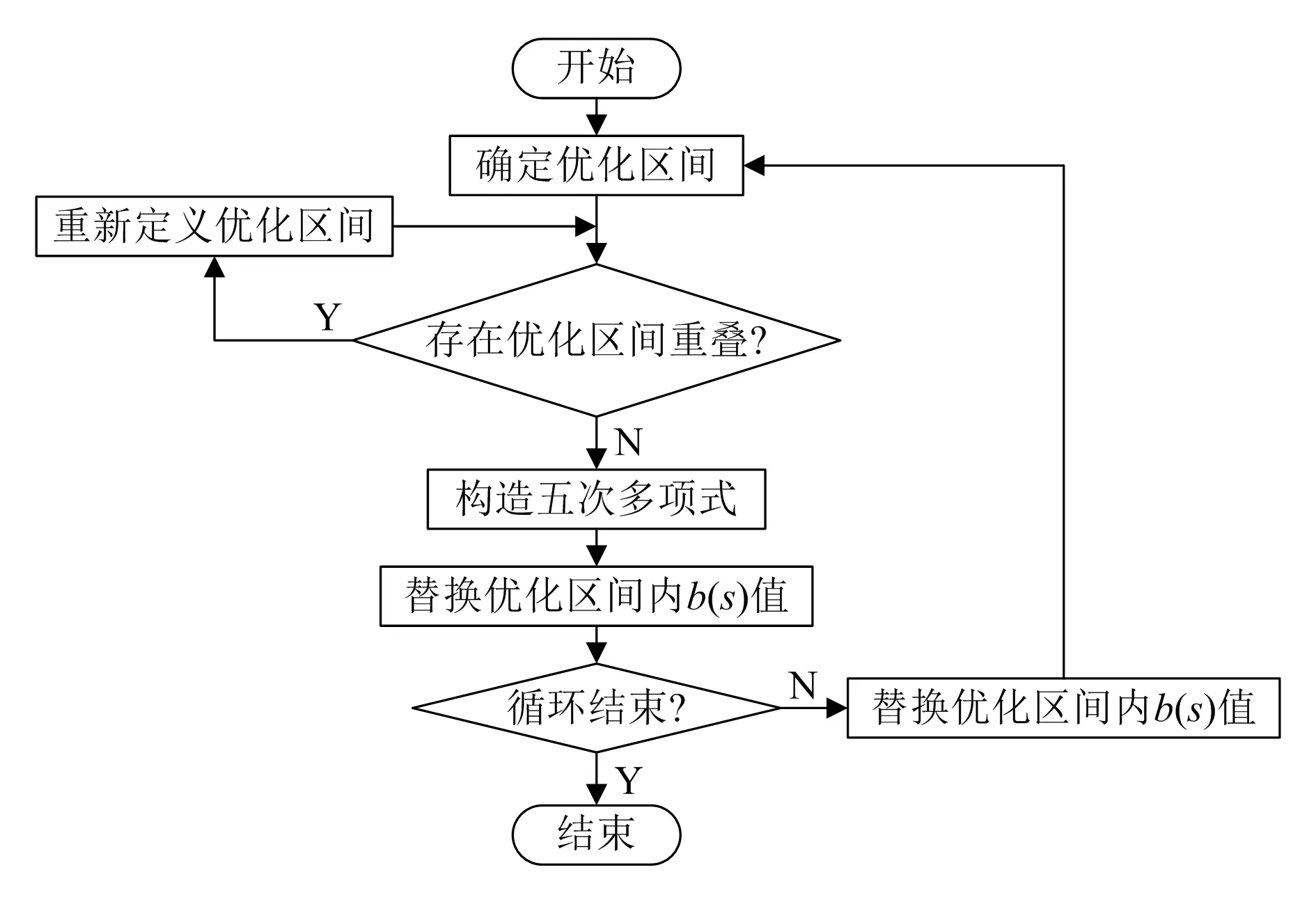
图2 局部优化处理流程图

具体处理方法如下：

步骤1,确定优化区间。所得冲击点的路径坐标是已知的，设kc为优化半径，即冲击点左右两边路径点的个数，以冲击点为中心的(2kc+1)个离散点所在的区间即为优化区间。

步骤2,判断是否存在优化区间重叠。判断方法为对相邻冲击点的路径坐标做差，若差值小于或等于2kc，则两个冲击点的优化区间存在相互重叠，执行步骤3；反之则不存在优化区间重叠，执行步骤4。

步骤3,重新定义优化区间。若两个相邻冲击点的优化区间存在重叠，则将两个优化区间合并为一个，考虑到可能存在两个以上冲击点优化区间重叠的情况，重复步骤2，判断是否仍然存在优化区间重叠的情况，若存在，则重复步骤3，直至循环条件不成立，执行步骤4。

步骤4,构造五次多项式。构造五次多项式的边界条件需要通过对原曲线上的离散点进行分析得到，由于对两端点要求的边界条件均为端点处的函数值、一阶导数值及二阶导数值，因此可分别求解。求解思路如下。

设五次多项式的表达式为：

b(s)=a0+a1s+a2s2+a3s3+a4s4+a5s5

(21)

对端点的约束条件为：

(22)

式中s0,sf分别为优化区间起点和终点的路径坐标，在每个冲击点均为已知量，端点边界条件已经由之前离散点求出时，亦作为已知量，因此方程组未知量仅为6个自变量系数，此时具有6个未知数和6个方程的线性方程组可求得唯一解，从而得到用于此优化区间的五次多项式。

步骤5,替换优化区间内b(s)值。得到所求五次多项式后，将优化区间内所有路径点的路径坐标代入多项式，从而得到优化后的b(s)值，此处所得的b(s)值即可用于之后计算新轨迹在此区间内的转矩值和轨迹执行时间等参数。对伪加速度项a(s)求导可得：

(23)

步骤6,判断循环结束条件。完成步骤5之后，对于一个冲击点的所有处理操作已经结束，所以接下来判断所处理的冲击点是否为所有冲击点中的最后一个，若判断结果为是，则针对冲击点的优化处理操作结束；若判断结果为否，则读取下一个冲击点路径坐标，并从步骤1开始重复循环，直至判断结果为是。

至此，本文得到一条无冲击的轨迹，机器人末端执行此轨迹可保证运动平稳无冲击。

3 算例与结果分析

为验证本文提出的轨迹规划方法的有效性，本文以3R串联机器人为研究对象，以机器人末端沿正弦曲线运动为例，在MATLAB中进行仿真计算。该机器人参数见表1。

表中m为连杆质量，r为连杆驱动关节与其质心之间的距离，JL和JT分别为各连杆相对于其质心在轴向和径向的转动惯量，l为关节之间的距离。连杆关节1,2,3的最大转矩分别为140 N·m、140 N·m、50 N·m。

表1 3R机器人参数

机器人末端执行器的路径为三维空间中经处理后的正弦曲线，如图3所示，其参数方程为式(24),其中s′为自变量。

(24)

图3 机器人末端路径

首先以时间最优轨迹规划算法针对此路径求解出机器人轨迹，然后根据式(19)中τk的表达式计算出机器人在所有路径点处各关节转矩，结果如图4所示。由图4可以看出，机器人执行时间最优轨迹时，各关节转矩均存在突变，且关节2在大部分路径点处输出转矩处于其极限值，且存在关节转矩从最大值瞬间变化为最小值的情况，从而表明时间最优轨迹存在冲击。

图4 时间最优轨迹关节转矩随路径坐标的变化情况

根据式(20)计算出此时间最优轨迹所有路径点的冲击函数值，结果如图5所示。由图5可知，在大多数路径点处，冲击函数值较小，即关节转矩变化率较小，不存在冲击；在少数特殊路径点处轨迹冲击函数值突然增加，通过与图4进行对比可知，此类路径点处关节转矩发生突变。

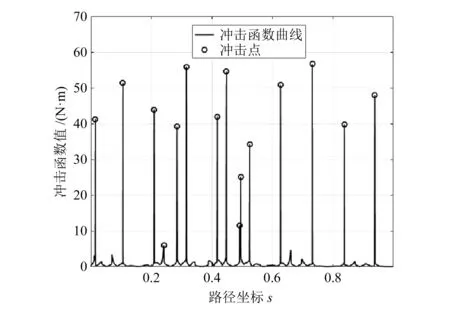
图5 时间最优轨迹冲击函数值随路径坐标的变化情况

针对上述冲击点，使用无冲击近似时间最优轨迹规划算法进行局部优化处理，得到无冲击轨迹。根据式(20)计算无冲击轨迹所有路径点处的冲击函数值，并与时间最优轨迹的冲击函数值进行对比，结果如图6所示。

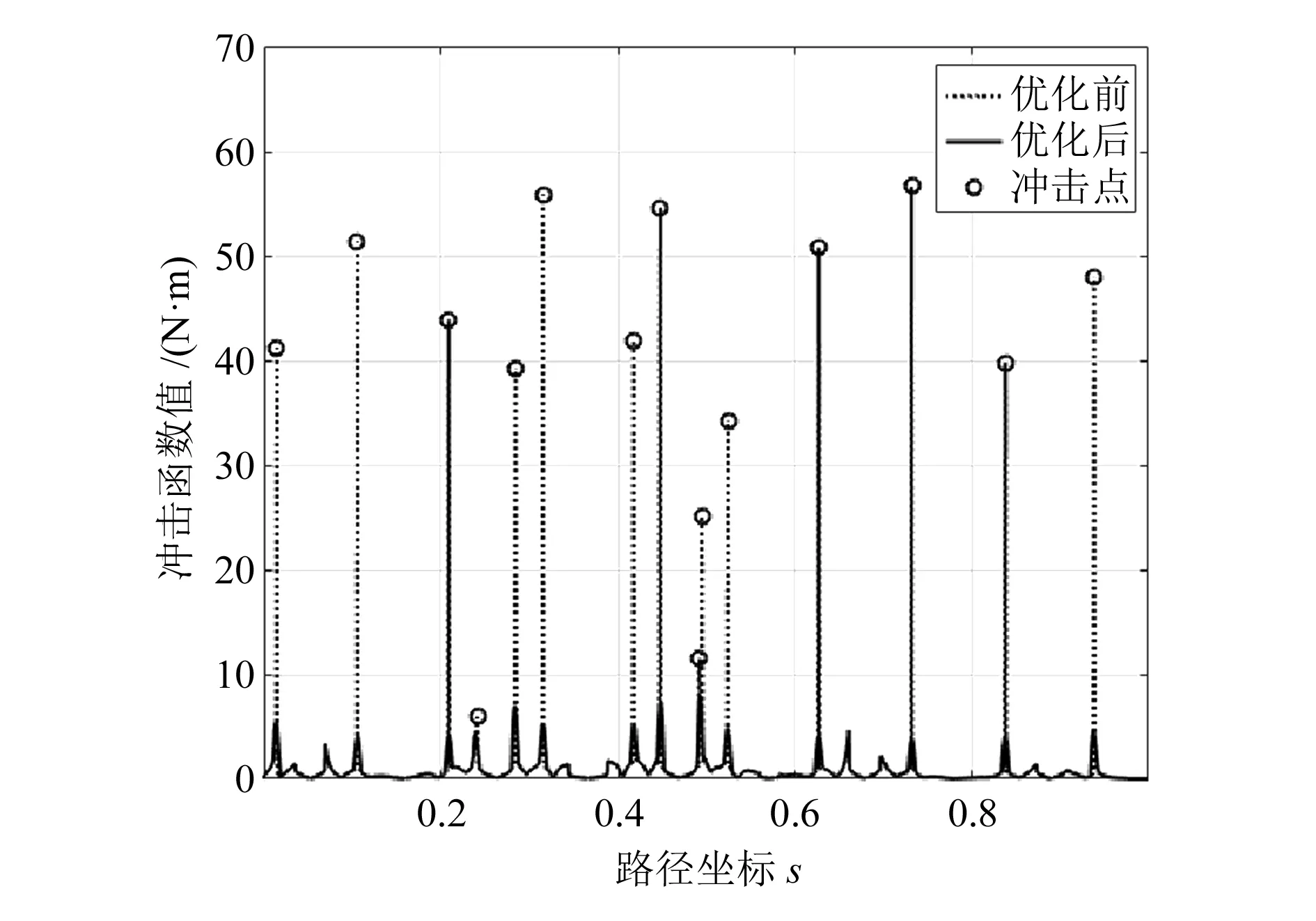
图6 两种轨迹冲击函数值变化情况对比

由图6可知，经无冲击近似时间最优轨迹算法优化处理后，无冲击的路径点处其冲击函数值与时间最优轨迹一致，即并未因优化处理过程本身产生新的冲击点；原冲击点处的冲击函数值明显减小。

根据式(19)中τk的表达式可计算出无冲击机器人在所有路径点处各关节转矩。无冲击近似时间最优轨迹规划算法针对冲击点进行局部优化处理，对于无冲击的路径点，各关节转矩与时间最优轨迹一致，因此图4与图7差别不大。为直观显示机器人执行两条轨迹时关节转矩的差别，选取3个典型的冲击点，以其所在优化区间内关节转矩的差异实现两条轨迹的对比。3个典型冲击点依次为冲击值最大的路径点s1,冲击值最小的路径点s2以及冲击函数值在所有冲击点中位于中位数的路径点s3。3个优化区间δ1,δ2,δ3内的转矩对比情况如图7所示。

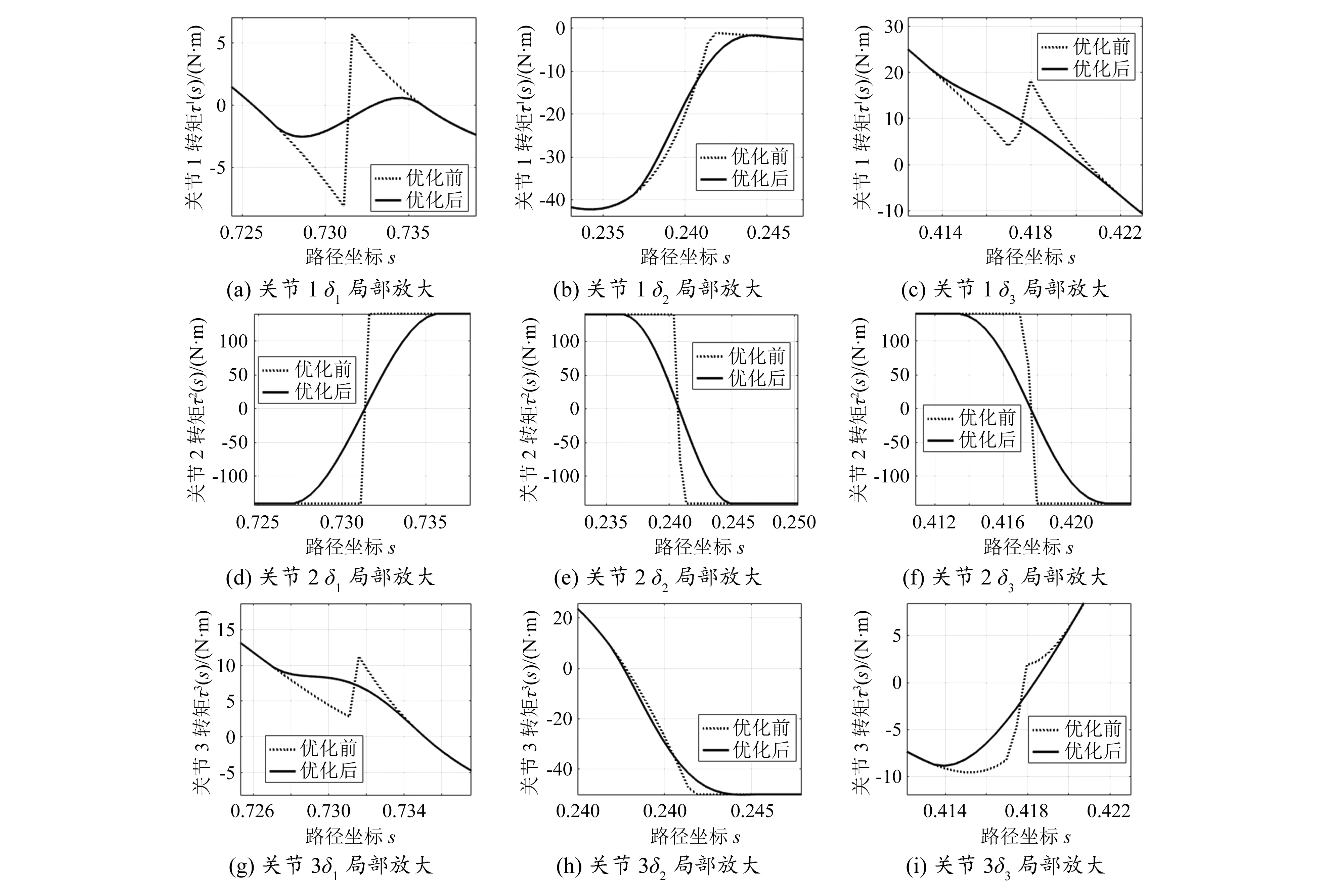
图7 典型优化区间内优化前后关节转矩对比

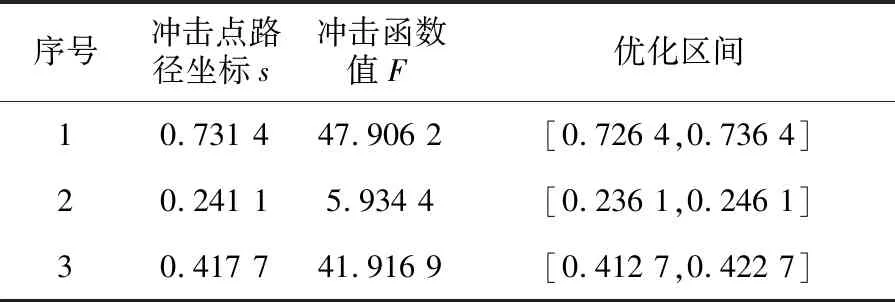
表2 3个典型优化区间相关参数

对于式(24)所表示的路径，使用MATLAB在相同的计算环境下(Windows 7操作系统，CPU 3.40 GHz)时间最优轨迹的执行时间为5.531 6 s，无冲击轨迹的执行时间为5.543 1 s，增加了0.21%(0.001 5 s)，因此无冲击轨迹在消除了冲击的情况下依然能够保证近似最优的执行时间。

综上所述，无冲击近似时间最优轨迹规划算法能够成功消除轨迹中的冲击，并能够保证轨迹时间的近似最优，从而能够实现机器人平稳高效地运行。

4 结束语

本文以3R串联型机器人为研究对象，对机器人时间最优轨迹规划问题进行了研究。首先通过建立参数空间把原本的多维优化问题转化到二维空间，然后将轨迹规划问题转化成二阶锥规划问题。在此基础上提出了一种考虑冲击的时间最优轨迹规划方法。该方法分3个步骤：第一步，建立冲击函数并筛选出冲击点；第二步，针对冲击点使用三次样条曲线在参数空间中对伪速度的平方项进行局部优化；第三步，由优化后的结果得到新的轨迹和各关节转矩的变化情况。该方法最主要的特点是对冲击点的筛选和针对性处理，从而使获得的轨迹执行时间短且运行平稳。最后，在MATLAB环境下进行了仿真计算，设置机器人末端路径为处理后的正弦函数曲线，通过对比优化前后各关节转矩的变化情况，验证了此轨迹规划方法的有效性。