基于节假日因素的多尺度犯罪时序预测方法研究

翟一鸣, 丁 宁,2, 李成龙

(1.中国人民公安大学侦查学院， 北京 100038; 2.中国人民公安大学公共安全行为科学实验室， 北京 102623)

0 引言

犯罪预测是建立现代化社会治安防控体系的重要问题之一。目前随着大数据、人工智能等技术的发展，公安机关建立了各类警务信息平台来监测当前以及预测未来的社会治安状况。对未来的犯罪状况进行预测不仅可以提前采取措施防止重大、恶性的犯罪发生，同时也是建立智慧城市的重要一环。

对犯罪案件的时序分析与预测一直是国内外犯罪分析和犯罪预防工作中的一种重要途径。目前可用于预测犯罪的方法主要有时序分析、神经网络等，但是应用神经网络等机器学习方法进行预测对犯罪现象的解释性不强，且在参数设置过程中还应考虑如何确保操作率的收敛性和一致性问题。因此时序分析方法作为一种传统的数据分析方法，不仅可以很好地解释犯罪数据的波动性，且其算法一直在不断优化和发展中，如本文所使用的Prophet就是一种新的时序算法。犯罪的时序分析和预测主要分为3种类型：(1)如Felson和Poulsen对一天内各时段犯罪模式的分析[1]、Gorr等人基于全市范围的数据利用Holt指数平滑度与每月的季节性变化对未来一个月犯罪的预测[2]。(2)结合地理因素，构建“space-time”类型的犯罪分析[3-4]，如Ye等人分析武汉的入室盗窃数据发现入室盗窃的时空聚类同时存在，且随着时间的推移，热点相对稳定[5]。(3)时序分析结合可能对犯罪产生影响的经济、环境等因素对犯罪进行预测[6-8]。然而其中很少有研究能将节假日因素完整纳入到模型中，国内外文章中仅有Cohn & Rotton于2003年统计了Minneapolis州的报警电话数据，并通过设置哑变量进行逻辑回归的方法发现暴力犯罪和财产犯罪均与重大(或法定)假日显着相关[9]。为提高模型预测的准确率，采用了Prophet模型来对犯罪时序进行分析和预测并将我国节假日因素完整地加入到模型中。

1 理论研究与方法

1.1 犯罪数据来源

时间序列(Time Series)就是一串按时间维度索引的数据，本文中与时间维度对应的是B市公安局的每日案件数量，其时间跨度为2004～2014共11年。犯罪类型的选择需要考虑两方面的因素：首先，犯罪量过少会在很大程度上影响预测的准确率，其次，不同案件数据量之间若存在较大差异也会影响结果的说服力。因此本文所选择的盗窃案件和诈骗案件的数量为2014年度发案量最高的两类案件，分别为6.7万件和5.2万件。本文规定在预测过程中，训练集为2004～2013年的所有数据，预测集为2014年的数据。最后将预测的案件数量与真实案件数量进行比较得出RMSE、MAE以及准确率。

随着社会经济的发展以及治安状况的不断改善，各类案件产生的数量和类型都发生了变化，本文中两种案件数据进行处理并绘制出折线图如图1(a)(b)所示。从图中可以看出：

(1)年际规律。盗窃类犯罪从2008年开始呈现下降趋势，其总体数量从2009年开始又有逐年上升的趋势；诈骗类犯罪案件数量逐年快速上升，直到2012年开始有所缓和。

(2)月际规律。两类犯罪数量均在过年期间进入全年的谷值，但在年前案件数量会攀升出现峰值，且在年后案件数量也会迅速上升；各类犯罪数量在年后达到峰值后开始周期性回落，且在国庆节前后会出现谷值。

(3)一周之内的规律。盗窃犯罪在周四有一个明显的谷值，周五开始回升并达到一周之内发案量最多，而诈骗案件的最高发案量在周二产生；盗窃案的总体趋势是周末的发案量高于工作日，诈骗案件是工作日发案量大于周末，且诈骗案件这种规律更加明显，其工作日的发案量远远高于周末的发案量。

1.2 ARIMA算法模型

传统的对时间序列的预测方法有很多种，如加权移动平均法、简单指数平滑法、霍尔特(Holt)线性趋势模型、霍尔特- 温特斯(Holt Winters)方法以及ARIMA模型等。ARIMA(Autoregressive Integrated Moving Average model)中文全称为自回归滑动平均模型，是一种流行的时序分析方法[10-12]。在ARIMA中，AR代表自回归模型，参数p是自回归项数；MA代表滑动平均模型，参数q为滑动平均项数；参数d是使时间序列平稳所需做的差分次数。实际上ARIMA(p,d,q)模型是ARMA(p,q)模型的扩展，ARIMA模型可以用以下公式表达：

(1)

其中L是滞后算子，d∈Z，d>0。

ARIMA模型本身也存在一些不足，如作为一种线性预测方法，可以很好地拟合数据内在的规律，但其样本需求量大，且缺乏灵活性，无法感知外部变量对自身的影响[13]。另外，ARIMA也不能自动化处理异常值，需要在使用之前对数据进行大量处理。Prophet工具可以很好地解决以上传统时序分析工具的缺陷，具有很强的灵活性和易用性。

1.3 Prophet预测算法模型

Prophet是Facebook公司于2017年发布的一款开源的时序分析工具，主要用来预测未来一段时间网站的访问量。Prophet将复杂的统计分析过程整合简化，且在拟合过程中可以处理异常值、突变点、季节性以及节假日效应等，提升了数据分析效率的同时提高了预测的准确率[14]。当前国内将Prophet应用于各领域的研究，主要有李丽萍等人利用Prophet算法来预测银行网点备付金，有效解决了“异常值”和“拐点”的预测问题，其预测准确率高于 ARMA 算法和LSTM 算法[15]；翟笃林等人将Prophet应用于电离层TEC异常识别，比较发现Prophet预测模型的预测精度比ARIMA模型方法高2.55倍左右，比滑动四分位法高10.74倍左右[16]；国外RONANKI等人利用WHO提供的关于青少年自杀的数据，利用线性回归、随机森林和Prophet方法在社交媒体上定位可能会自杀的青少年人群[17]；YASSIR等人提出了一个用于预测单个地理区域在给定的时间t是否将达到联合国可持续发展目标的框架，并在框架中使用了ARMA、ARIMA和Prophet模型作为比较，其中Prophet取得了最好的预测效果[18]。

Prophet模型中除了考虑季节项，趋势项和剩余项3项内容外，还将节假日效应考虑在内，如公式(2)所示。其中gt，st和t分别代表趋势项、周期项和剩余项，ht代表节假日项。Prophet通过拟合以上四项，最后把它们结合起来就得到了时间序列的预测值。

yt=gt+st+ht+t

(2)

其中，对于趋势项gt而言，当增长率k不变时：

(3)

(4)

那么在时间t上的增长率可转换为k+aTδ. 增长率k确定之后，在拐点Sj(j=1,2,…m)自适应调整偏移量项，参数m也要随之确定，通过数学公式表示为：

(5)

g(t)的表达式可表示为公式6，其中a(t)=(a1(t),…,aS(t))T，δ=(δ1,…,δS)T，γ=(γ1,…,γS)T. 由于g(t)是基于逻辑回归函数和分段线性函数，对于分段线性函数而言，g(t)的表达式还可简化为公式7。其中k是增长率，δ是增长率的变化量，且服从拉普拉斯分布。

(6)

g(t)=[k+a(t)Tδ]t+[m+a(t)Tγ]

(7)

s(t)表示季节性趋势，以傅里叶级数来模拟时间序列的周期性，时间序列的周期为P，不论是以年为周期P=365.25，还是以星期为周期P=7，其傅里叶级数都可以表示为：

(8)

在Prophet中N的设定要考虑到P的值，P=365.25时N=10，P=7时N=3，可设置参数β=(a1,b1,…,aN,bN)T,通过设定公式9可将公式8可转换为公式10，其中β的初始化是β～Normal(0,σ2).

(9)

s(t)=x(t)β

(10)

h(t)是节假日效应，在Prophet中不同的节假日之间被认为是相互独立的，对第i个节假日来说，Di表示该节假日日期前后的一段时间，参数ki表示节假日的影响范围，同时引入指示函数Z(t),假设有L个节假日，那么

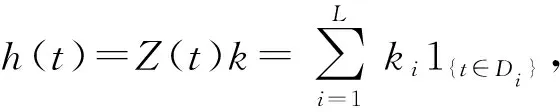
(11)

其中k～Normal(0,v2)，v的默认值为10，可以在计算中自定义调整，v的值越大表示节假日对该模型的预测效果影响越大。

2 犯罪时序预测方案的设计及优化

2.1 引入节假日因素优化预测模型

为分析犯罪案件数据的规律，减少由于统计错误出现的误差，首先对预测方法进行3次优化，方案优化的流程见图2。第1组方案为Prophet和ARIMA的原始模型，此为对照组；第2组方案是利用Prophet内建的holiday函数添加节假日变量，内建函数包含的节假日信息为：元旦、春节、清明节、劳动节、端午节、中秋节以及国庆节。但是我们发现每个节日只设定在一天之内，这不符合我国节假日的放假周期为3天或7天的国情，因此我们建立了2004～2014年每年的节假日列表，并将该列表导入Prophet的holiday函数形成第3组优化。第4组优化是在处理数据的过程中，发现每月1日的发案量远高于本月其他日期，经于公安部门实地考察后判定每月1日的案件数量存在一定的统计错误，因此将每月1号的案件数量处理为异常值。以盗窃案为例对4组优化的效果进行比较，同时区分Prophet的加法模型和乘法模型，在表1可以看出第4组方案具有最好的预测效果。

表1 4组预测方案效果对比

图2 预测方案优化流程图

2.2 Prophet和ARIMA模型的预测结果分析

在得出最优方案的基础上，分别利用Prophet和ARIMA对2004～2013年的盗窃案件和诈骗案件的发案数量进行训练，并从未来一周、一月和一年3个时间尺度来预测2014年的发案量。预测未来一年的数据时所使用的数据量为前10年的每日犯罪数据；预测未来一月的数据时所使用的是上一月份及其之前所有月份的数据；预测未来一周的数据时所使用的是被预测周之前的每周的数据，为避免节假日和每月1号误差的影响，特选择每月的第3个完整星期。如果每月的第3个完整星期的实际日期和其他月份实际日期相差太大，可适当调整为前一个或后一个星期，以此来保证预测周期选择的最大的相近性。因此，在2014年一年中存在可预测的12组未来一周的犯罪、12组未来一月的犯罪以及1组未来一年的犯罪，并使用均方根误差(RMSE)、平均绝对误差(MAE)和预测日期内的平均准确率对预测结果进行检验。利用Prophet对盗窃、诈骗犯罪在2004～2014年的趋势拟合见图3(a)(b)，表2为模型的预测结果。

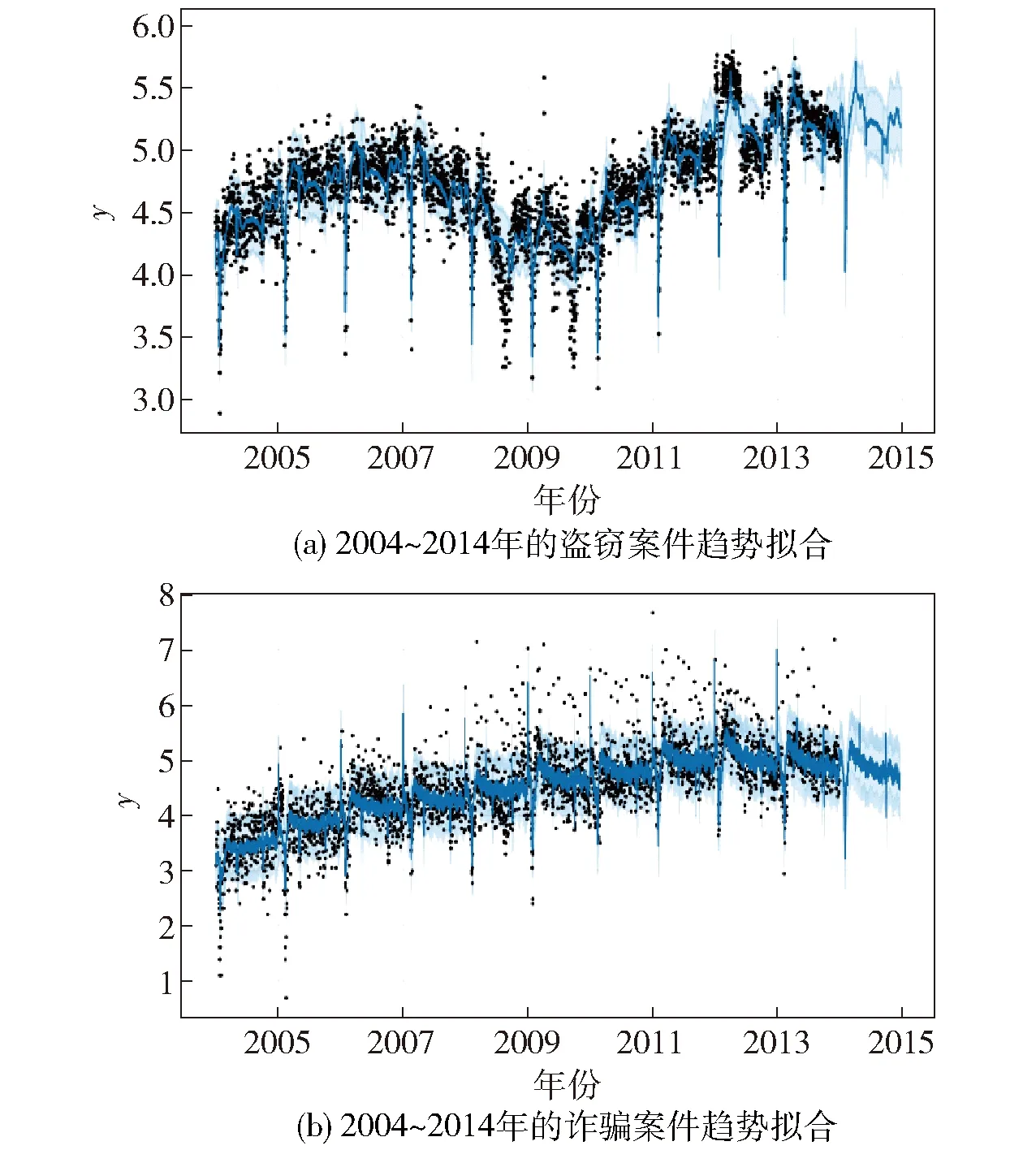
图3 2004～2014年的盗窃案件和诈骗案件趋势拟合

从表2中可以看出：(1)对于短期预测特别是未来一周的预测，ARIMA模型对盗窃案件预测的准确率更高，对于长期预测如未来一年的预测，Prophet模型在这两类案件中都更具优势；(2)对于诈骗案件而言，Prophet的加法模型一直是最优的预测模型，对于盗窃案件而言，预测未来一周和一月都应选择ARIMA模型；(3)ARIMA模型具有良好的短期预测性能，其对盗窃案件的预测准确率达到88.99%，比Prophet模型高出4.86%；加入节假日因素的Prophet模型在各时间尺度上均衡性更强，且对两类犯罪的长期预测准确率均高于ARIMA模型，达到83.69%和82.49%。

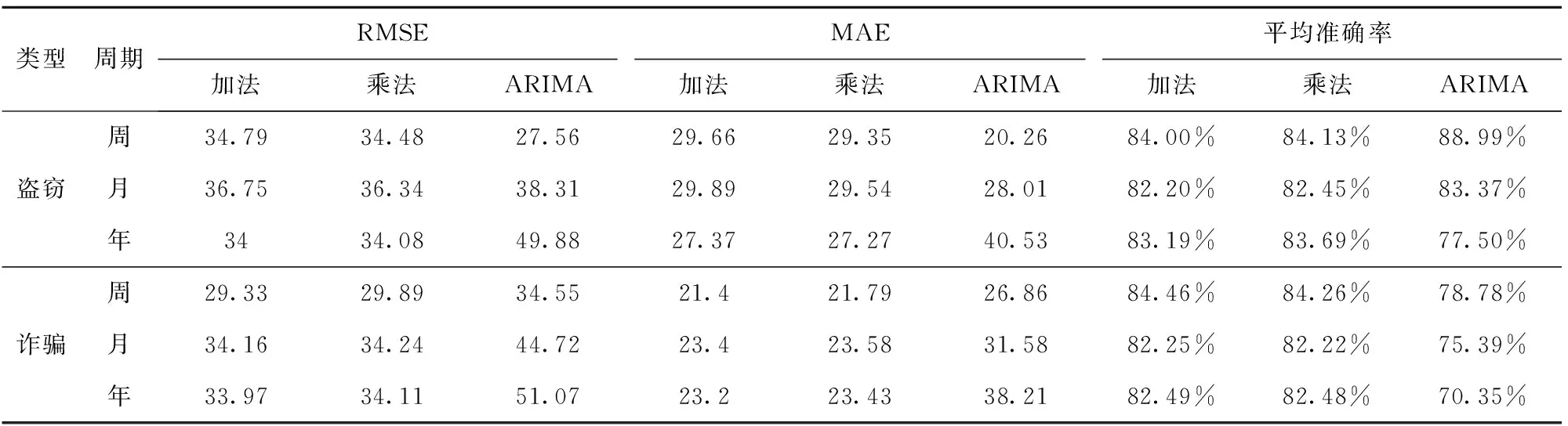
表2 利用Prophet和ARIMA模型对两类犯罪进行预测的结果比较

从上述对预测结果的分析中可以看出，模型选择主要以预测周期的长短为依据，为了进一步探究模型的效果是否与案件类型有关，表3选取了5类案件均以年为周期进行预测，可以发现即使是盗窃—盗窃自行车、抢劫—入室抢劫，这些属于同一类的案件其最优模型也是不同的；发案量越大，Prophet模型越优于ARIMA模型。综上所述，模型的预测效果与案件类别之间不存在明显的关系，而与预测周期的尺度及发案数量存在一定关系。

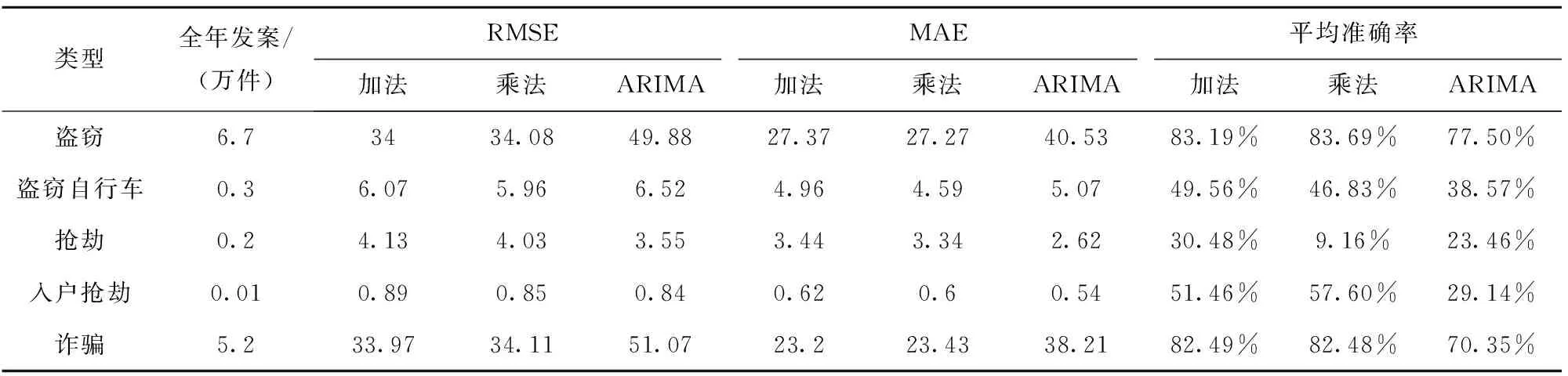
表3 5类案件周期一年的Prophet和ARIMA模型预测结果

3 结论

本文首先分析了盗窃案和诈骗案在年际、月际以及一周之内的分布规律，然后基于犯罪数据特点以及我国节假日的特殊性对预测方案进行优化。在利用Prophet和ARIMA对犯罪案件进行时序预测时，发现ARIMA在短期预测具有良好的性能，Prophet模型具有更好的均衡性，且在长期预测时Prophet的模型远优于ARIMA模型。因此，在分析城市未来短期的治安状况、为未来短期内的社会治安防控工作做准备时，可选择ARIMA模型来预测犯罪状况；分析城市未来长期的社会安全事件发生规律时，或者为较长时间后的城市大型活动做准备时，应选择Prophet模型作为预测工具。

利用社会安全事件历史数据来预测未来的犯罪状况可至少带来3个方面的益处。第一，优化警力配置。可根据未来一段时间对犯罪趋势的预测，合理安排警力资源，当未来犯罪较少时只配备所需的最低警力即可处理各项警情，此时可适当减少出勤民警数量；如果预测未来可能发生犯罪数量较多时，可提前抽调其他警组的警力协助执勤，以防警力不足来稳定当前的治安形势。第二，开展专项行动。在预测未来的犯罪趋势持续走高时，可组织专项打击活动，减少某类犯罪严重影响人们的正常生活。第三，服务国家大型活动预案。社会治安环境是决定一个城市能否开展国家大型活动的重要因素之一，不仅要考察该城市以往的犯罪态势，还要考虑未来活动开展期间可能的犯罪状况，并提前布置相应力度的社会治安清理整治任务。此外，还可为活动过程中与犯罪有关的紧急预案提供参考。

在未来对社会安全事件发生规律的分析和利用过程中，应借助各种机器学习模型将包括节假日、大型活动、政策影响和自然环境等一系列因素纳入其中，来满足不同时间跨度的犯罪预测的需要，不仅在宏观角度上服务于省市的厅局级警务部门，实现为警务高级决策人员提供决策参考的战略性目标；同时，还为公安分局、派出所等实战部门的具体警务活动提供技术性情报支持。