Maximizing deviation method for multiple attribute decision making under q-rung orthopair fuzzy environment
Jie Wng , Gui-wu Wei ,*, Cun Wei , Jing Wu
a School of Business, Sichuan Normal University, Chengdu, 610101, PR China
b School of Statistics, Southwestern University of Finance and Economics, Chengdu, 611130, PR China
Keywords:
ABSTRACT Because of the uncertainty and subjectivity of decision makers in the complex decision-making environment, the evaluation information of alternatives given by decision makers is often fuzzy and uncertain. As a generalization of intuitionistic fuzzy set (IFSs) and Pythagoras fuzzy set (PFSs), q-rung orthopair fuzzy set (q-ROFS) is more suitable for expressing fuzzy and uncertain information. But, in actual multiple attribute decision making (MADM) problems, the weights of DMs and attributes are always completely unknown or partly known,to date,the maximizing deviation method is a good tool to deal with such issues. Thus, combine the q-ROFS and conventional maximizing deviation method, we will study the maximizing deviation method under q-ROFSs and q-RIVOFSs in this paper. Firstly, we briefly introduce the basic concept of q-rung orthopair fuzzy sets (q-ROFSs) and q-rung interval-valued orthopair fuzzy sets (q-RIVOFSs). Then, combine the maximizing deviation method with q-rung orthopair fuzzy information, we establish two new decision making models. On this basis, the proposed models are applied to MADM problems with q-rung orthopair fuzzy information. Compared with existing methods, the effectiveness and superiority of the new model are analyzed. This method can effectively solve the MADM problem whose decision information is represented by q-rung orthopair fuzzy numbers (q-ROFNs) and whose attributes are incomplete.
1. Introduction
Since the reform and opening up, China’s economic and social development is relatively rapid.Especially in recent years,with the acceleration of the pace of social construction and the deepening of urbanization, China’s architectural engineering ushered in an unprecedented development space. People from all walks of life are paying more and more attention to the quality of construction projects.As an important aspect closely related to people’s life and property safety, the quality of construction projects will directly depend on the quality of building materials.Therefore,it is of great significance to strengthen the inspection of building materials for the control of construction quality. Generally speaking, inspection of building materials is an in-depth inspection of the quality of building materials, which is a comprehensive quality inspection before the construction of projects. The application of building materials with standard quality in the construction process can not only ensure the overall quality and service life of the building to improve, but also ensure the life safety and construction safety of the construction personnel, in addition, it can achieve better expansion and extension of the form and structure of the building.Similarly, if the quality of building materials cannot be effectively guaranteed, it will have a direct impact on the development of construction projects, seriously affect the overall quality of construction projects,and even threaten the service life of construction projects,which is related to the life safety of construction workers.Through the past construction problems, we can find that the current occurrence of building collapse accident frequency is high,the direct reason for this kind of problem is that the construction unit in the construction process of the use of building materials,failed to comply with the requirements and specifications to do the inspection work. Based on this, in order to make the construction quality meet the standard,the quality of building materials should be strengthened to ensure the quality and performance of building materials.
In previous study, some research article about building materials identification have been worked by lots of scholars. For instance, Suchorab, Frac, Guz, Oszust, Lagod, Gryta, Bilinska-Wielgus and Czerwinski [1] proposed an early building materials detection and identification of fungal contamination method using an electronic nose. Stastnik, Vala and Kninova [2] built an numerical algorithm to identify the basic thermal technical characteristics of building materials. Ito and Takigasaki [3] developed the multitarget identification model for emission parameters of building materials. Rouchier, Woloszyn, Kedowide and Bejat [4] given the covariance matrix adaptation evolution strategy to identify the hygrothermal properties of building envelope materials. Ma, Dang and Shan [5] studied and analyzed the potential fire-proof energy building material based on artificial leather.Wang,Wang,Wei and Wei [6] presented some q-rung orthopair fuzzy cosine similarity measures and cotangent similarity measures to identify building materials.However,all above mentioned methods and tools may be difficult to apply in practical decision making problems. Firstly,these existing identification methods of building materials have high professional and technical requirements, so it is difficult to apply these methods to practical problems. Secondly, in these identification models, evaluation results are represented by real Numbers. However, in actual decision-making problems, it is not accurate to only use real Numbers to represent evaluation results due to human subjectivity and uncertainty.Therefore,it is of great importance to find a reasonable way to depict evaluation information and use appropriate tools to get reasonable evaluation results.
To data, the intuitionistic fuzzy set (IFS), which was given by Atanassov [7], can depict the human subjectivity and uncertainty by membershipμ and non-membership ν,and μ+ ν ≤1.Thus,the IFS has been considered as an effective tool to study MADM problems since it was put forward [8-22]. Moreover, to extend the scope of assessment information, Pythagorean fuzzy set (PFS)[23,24],which satisfies μ2+ν2≤1,has emerged to deal with more complicated practical applications [25-31]. According to the IFS and PFS, Yager [32] further given the concept of the q-rung orthopair fuzzy set (q-ROFS) which satisfies μq+ νq≤1,q ≥1. So we can derive that the q-ROFS is a appropriate tool for practical decision making applications. Besides, in practical MADM problems,the weights of attributes and DMs are always partly known or completely unknown. However, the existing study about q-ROFS always assume the weights of attributes are completely known.Thus, these approaches can be difficult to apply in actual decision making problems.to conquer this limitation,Wang[33]developed the maximizing deviation method for such MADM problems. It’s clear that the maximizing deviation method can deal with more complex decision making applications.
The innovation and contribution of this article is proposing the q-rung orthopair fuzzy maximizing deviation method and the qrung interval-valued orthopair fuzzy maximizing deviation method to solve the MADM problems which the weights of attributes and DMs are incomplete. To introduce the maximizing deviation method under the q-rung orthopair fuzzy environment in detail,this paper is set out as follows. Section 2 reviews some related works about the q-ROFSs and the maximizing deviation method.Section 3 introduces some basic theories about q-ROFSs and q-RIVOFSs.Section 4 combines maximizing deviation method with q-ROFSs and q-RIVOFSs to build two new decision making models.Of course, the calculating steps of our proposed models are briefly denoted. In Section 5, we give two numerical examples for construction scheme selection with q-ROFNs and q-RIVOFNs and gave some comparative analysis. Section 6 concludes the paper with some remarks.
2. Literature review
Since the q-ROFS [32] was put forward, a large number of scholars have investigated and studied it [34]. In terms of aggregation operators, Liu and Wang [35] introduced some basic weighted average (WA) operators and weighted geometric (WG)operators under the q-rung orthopair fuzzy environment. Joshi,Singh,Bhatt and Vaisla[36]extended the q-ROFS to interval-valued environment. Wang, Wei, Wang, Lin and Wei [37] defined some dual hesitant q-rung orthopair fuzzy Hamacher aggregation operators. Xing, Zhang, Zhou and Wang [38] given some q-rung orthopair fuzzy point weighted operators.Xing,Zhang,Zhu and Bai[39] developed some uncertain linguistic choquet integral operators to fuse q-rung orthopair fuzzy information. Ju, Luo, Ma and Wang [40] put forward some q-rung orthopair fuzzy generalized power aggregation operators. Based on the Maclaurin Symmetric Mean (MSM) operator, Wei, Wei, Wang, Gao and Wei [41] developed some q-rung orthopair fuzzy MSM operators,Bai,Zhu,Wang and Zhang [42] given some q-rung orthopair fuzzy Partitioned MSM operators and Liu, Chen and Wang [43] presented some qrung orthopair fuzzy Power MSM operators. Based on the Bonferroni Mean (BM) operator, Liu and Liu [44] proposed some q-rung orthopair fuzzy BM operators, Liu and Liu [45] presented some Power PBM operators under the linguistic q-rung orthopair fuzzy environment, Yang and Pang [46] put forward some q-rung orthopair fuzzy Partitioned BM operators and Liu and Wang [47]developed some q-rung orthopair fuzzy Archimedean BM operators.Based on the Heronian mean(HM)operator,Liu,Wang and Liu[48] studied some q-rung orthopair fuzzy HM operators,Wei, Gao and Wei [49] defined some q-rung orthopair fuzzy HM operators and q-rung orthopair 2-tuple linguistic HM operators and Xu,Shang,Wang,Wu and Huang[50]introduced some dual hesitant qrung orthopair fuzzy HM operators. Based on the Muirhead mean(MM) operator, Wang, Zhang, Zhu, Zhou, Shang and Li [51] proposed some q-rung orthopair fuzzy MM operators, Gao, Ju, Zhang and Ju [52] defined some interval-valued q-rung orthopair fuzzy Archimedean MM operators,Liu and Liu[53] put forward some qrung orthopair fuzzy Power MM operators and Wang,Wei,Wei and Wei [54] studied some dual hesitant q-rung orthopair fuzzy MM operators.Based on the Hamy mean(HM)operator,Wang,Wei,Lu,Alsaadi, Hayat, Wei and Zhang [55] developed some q-rung orthopair fuzzy HM operators and Wang, Gao, Wei and Wei [56]extended these operators to interval-valued environment. In addition, some decision making methods and tools about the q-ROFS are studied by scholars. Liu, Chen and Peng [57] proposed some q-rung orthopair fuzzy cosine similarity measures and distance measures, Peng and Liu [58] presented some information measures about the q-ROFS and Wang, Wang, Wei and Wei [6]introduced some cosine and cotangent similarity measures between q-ROFSs.
As for the maximizing deviation method, Wu and Chen [59]handled the maximizing deviation method to study MADM problems with linguistic information. Wei [17] investigated the maximizing deviation method under intuitionistic fuzzy environment.Liang, Zhang and Liu [60] proposed some aggregation operators under the interval-valued Pythagorean fuzzy environment and used the maximizing deviation method to deal with MADM problems. Sahin and Liu [61] built two new neutrosophic models by using maximizing deviation method and applied them in MADM problems. Selvachandran, Quek, Smarandache and Broumi [62]proposed the single-valued neutrosophic TOPSIS model and utilized the maximizing deviation method for MADM. Xiong and Cheng [63] presented a novel method to compute the attribute’s weights by maximizing deviation method with neutrosophic information. Pamuˇcar, Sremac, ´Cirovi´c and Tomi´c [64] built the LNN WASPAS model and utilized the maximizing deviation method to determine the attribute weights.
According to the above literature review,we can find that the q-ROFS has the advantage of depicting more fuzzy assessment information and the maximizing deviation method can deal with MADM problems with incomplete attribute weights. To combine the two advantages,this paper is going to propose q-rung orthopair fuzzy maximizing deviation method to handle actual decision making applications effectively.
3. Preliminaries
3.1. The q-rung orthopair fuzzy set
According to previous literature research, the basic concept,score and accuracy functions, some comparative and operation laws about q-ROFSs [32] are depicted as below.
Definition 1.[32]. Let X be a fix set. A q-ROFS can be describe as
where μP: X→[0,1] means the function of membership degree(MD) and νP: X→[0,1] means the function of non-membership degree(NMD)which satisfies

According to the MD and NMD, The function of indeterminacy membership degree (IMD) can be computed as:To simplify Eq.
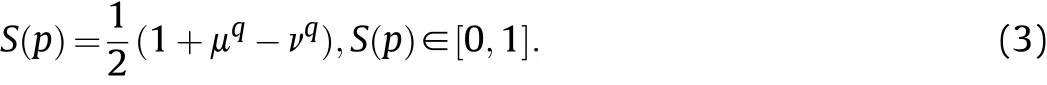
Definition 3.[32]. Given p=(μ,ν) as a q-ROFN, an accuracy function can be calculated as:

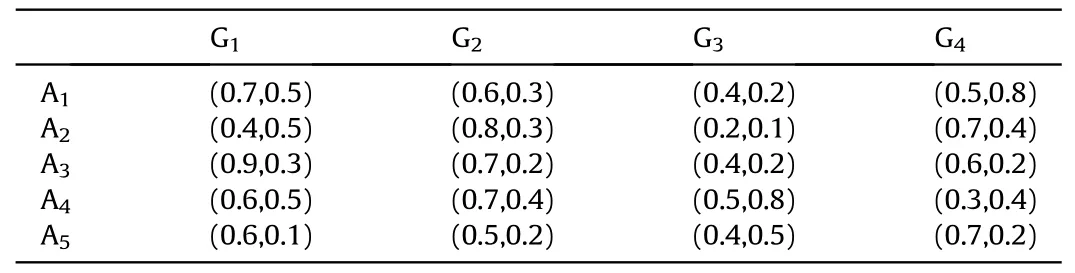
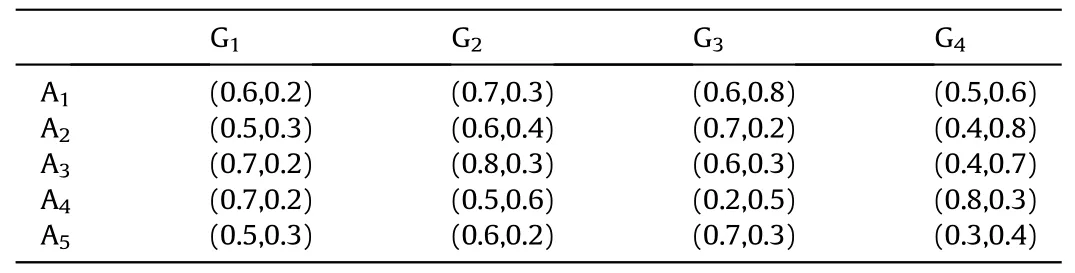
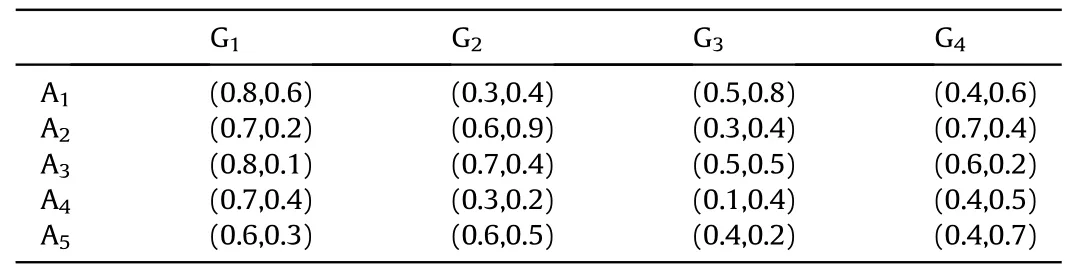
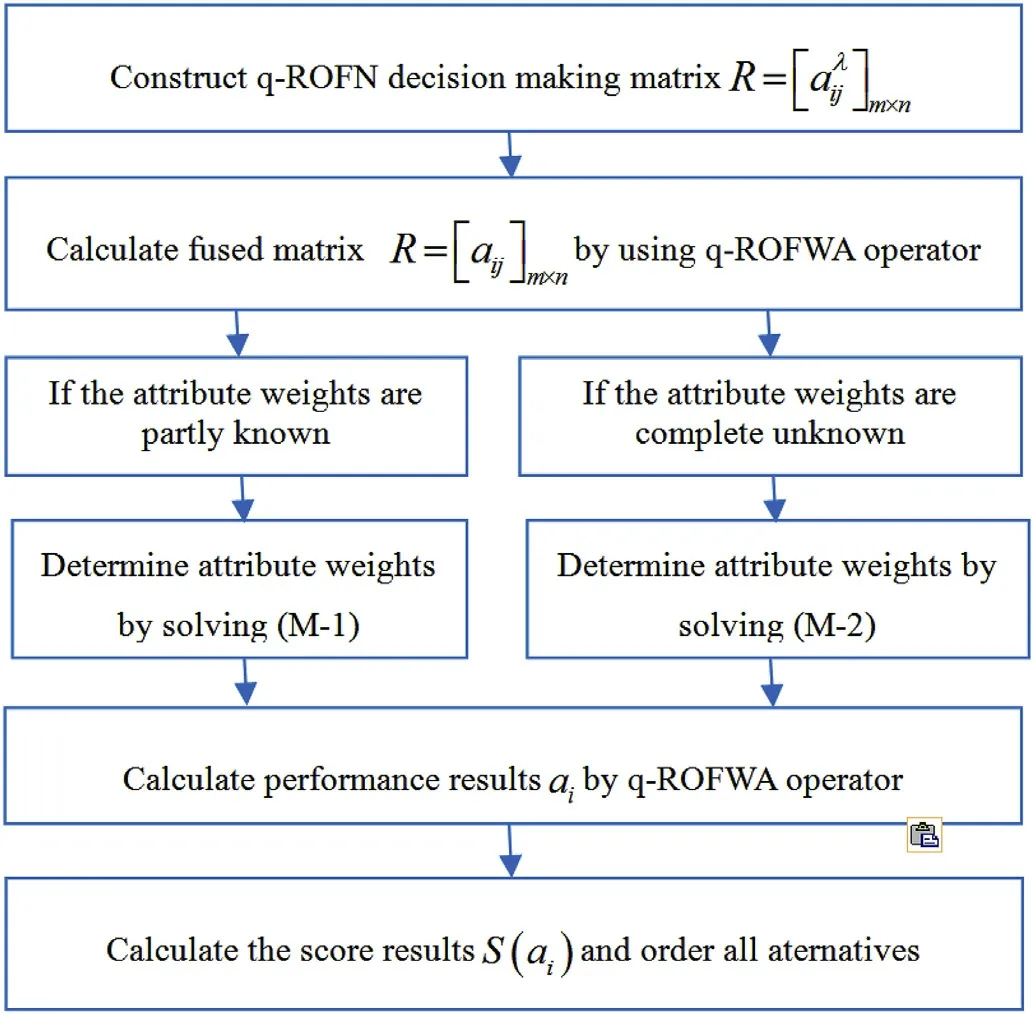
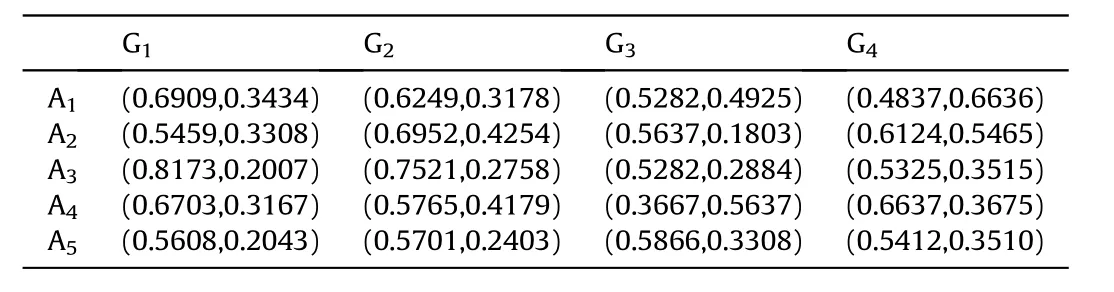
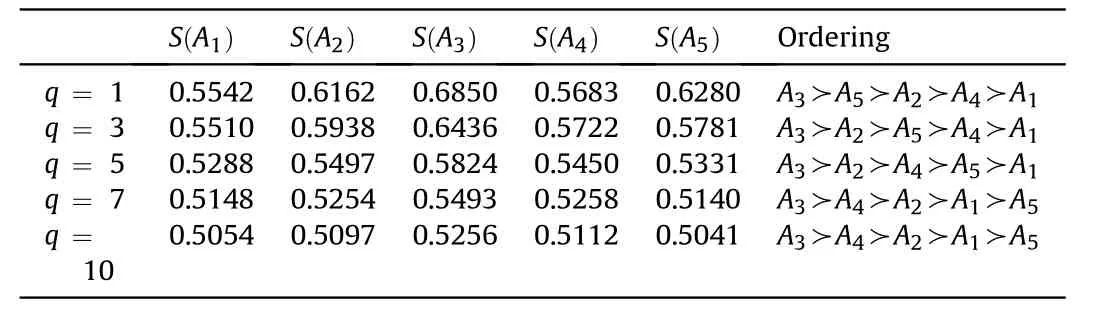
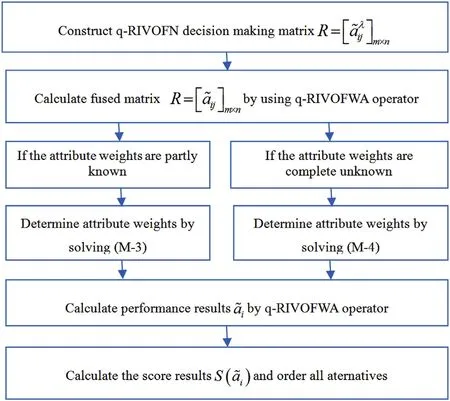
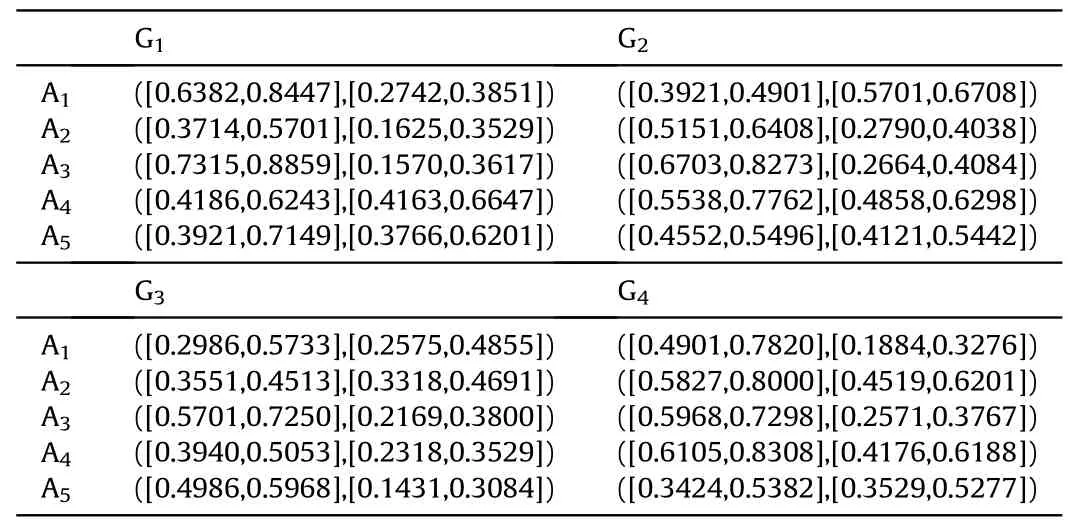
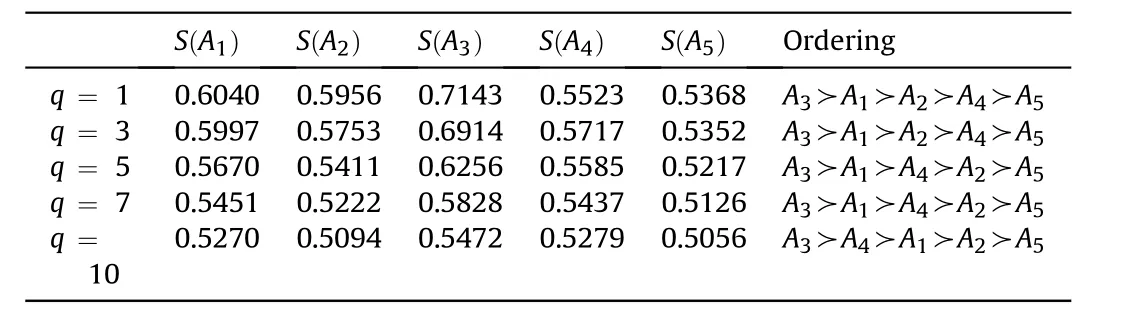
Definition 4.[49]. Let p1=(μ1,ν1) and p2=(μ2,ν2) be two q-ROFNs,be the scores of p1and p2, respectively, and let H(p1)=(μ1)q+(ν1)qand H(p2)=(μ2)q+(ν2)qbe the accuracy degrees of p1and p2,respectively,then if S(p1) Definition 5.[65].Given three q-ROFNs as p1=(μ1,ν1),p2=(μ2,ν2), and p = (μ, ν), and some operations laws of them can be expressed as: Example 1.Let p=(0.6,0.5),p1=(0.7,0.8)and p2=(0.9,0.3)be three q-ROFNs,suppose q =3,λ =2,then according to Definition 5,we can derive (1), we named p=(μ,ν) a q-ROFN. Definition 2.[49]. Given p=(μ,v) as a q-ROFN, a score function can be calculated as: Definition 6.[65]. Let pj=(μj,νj)(j=1,2,…,n) be a list of q-ROFNs with weighting vector be wj= (w1,w2,…,wn)T, thereby satisfying wj∈[0,1] and ∑nj=1wj= 1, then the q-rung orthopair fuzzy weighting average operator can be depicted as: According to the theories of q-ROFSs and the interval values,the basic concept,score and accuracy functions,some comparative and operation laws about q-rung interval-valued orthopair fuzzy sets(q-RIVOFSs) [32,36] are introduced as below. Definition 7.[56].Let X be a fix set.A q-RIVOFS can be expressed as Definition 8.[56]. Given ~p=([μL,μU],[νL,νU]) as a q-RIVOFN, a score function can be calculated as: Definition 9.[56]. Given ~p=([μL,μU],[νL,νU]) as a q-RIVOFN, an accuracy function can be calculated as: Definition11.[56]. Letand some operations laws of them can be expressed as:three q-RIVOFNs,E xample 2.Let ~p =([0.6,0.7],[0.4,0.5]), ~p1=([0.2,0.3],[0.7,0.8])and ~p2=([0.4,0.5], [0.5,0.6]) be three q-RIVOFNs, suppose q = 3,λ = 2, then according to Definition 11, we can derive{d1,d2,…dλ}with weighting vector be(ω1,ω2,…,ωλ),then we can compute the degree of difference between each alternative by maximizing deviation method and the computing equation of de- Definition 12.[56]. Let ~pj=([μLj,μUj],[νLj,νUj])(j=1,2,…,n) be a list of q-RIVOFNs with weighting vector be wj= (w1,w2,…,wn)T,thereby satisfying wj∈[0,1] and ∑nj=1wj= 1, then the q-rung interval-valued orthopair fuzzy weighting average operator can be expressed as:viation is listed as follows. In practical multiple attribute multiple experts decision making(MAMEDM) problems, fusing fuzzy evaluate information by utilizing aggregation operators is a useful tool to order all the alternatives. However, due to the complex decision-making environment, we always cannot obtain complete information and the attribute’s weight is always partly unknown or completely unknown, thus, how to allocate the attribute’s weight is an important issue. The maximizing deviation method, which proposed by Wang[33],has been used to handle such MADM problems in many decision-making fields. As we all know, it’s easy to select the better alternatives by ranking the fused values,in order to show the difference between all the alternatives more clearly, when an attribute exerts a significant influence on ranking results, it’s clear that this attribute is important to influence decision results and should be assigned with a big weight. On the contrary, if an attribute can only cause little changes on ordering of alternatives, it means this attribute is indifferent of decision process and should be allocated smaller weight. In other words, we need to give smaller weight to the alternative which creates smaller difference and give bigger weight to the alternative which creates clear deviation. Given m alternatives {A1,A2,…Am}, n attributes {G1,G2,…Gn}with weighting vector be (w1,w2,…,wn) and λ experts indicates the assessment information of alternatives Aiabout attributes Gjby experts dλand wjmeans the attribute’s weight which satisfies 0 In actual decision making problems, the attribute’s weights are always unknown or partly known,to deal with such issues,in this chapter, consider maximizing deviation method and q-ROFSs environment, we will construct the following nonlinear programming model to compute attribute’s weight. Case 1.If the attribute’s weights are partly known and the incomplete attribute’s weights are given as follows. 1) A weak ordering: {wi≥wj}; 2) A strict ordering: {wi- wj≥ δi(>0)}; 3) An ordering with multiples: {wi≥ δiwj},0 ≤ δi≤1; 4) An interval ordering: {δi≤wi≤ δi+ εi},0 ≤ δi<δi+ εi≤1; 5) An ordering of differences:{wi- wj≥wk- wl}(j ≠k ≠l). Then the nonlinear programming model can be constructed as: To solve this model, we construct the Lagrange function: where π is the Lagrange multiplier. Then we differentiate Eq.(16)with respect to wjand π,and the results of partial derivatives are set to zero, then we can obtain following equation; where ωλpresent the weights of dλand According to deal with the model(M - 1), we can get the optimal solution w = (w1,w2,…,wn)T, which means the attribute weights. Case 2.If the weight of the attribute is completely unknown,then the nonlinear programming model can be constructed as: Based on the results of partial derivatives and Eq. (16), we can get the following equation to obtain attribute’s weights. by normalizing Eq. (17), the normalized results are listed as: 4.1.1. The decision-making model 1 Based on maximizing deviation method, the MADM problems with incompletely attribute’s weights under q-ROFSs environment can be solved by following steps. Step 1.Construct decision making matrix R=[aλij]m×n,i=1,2,…,m,j=1,2,…,n where aλijmeans assessment information expressed by q-ROFNs. Step 5.Calculate the score results S(ai) (i=1,2,…,m)of ai(i =1,2,…,m),then the ordering of alternative Ai(i=1,2,…,m)can be derived by S(ai), the bigger S(ai) is, the better alternative Aiis. Step 6. Order all the alternatives Ai(i=1,2,…,m) based on S(ai) (i = 1,2,…,m). Step 7. End. Similar to q-ROFSs, in this part, consider maximizing deviation method and q-RIVOFSs environment, we will construct the following nonlinear programming model to compute attribute’s weight. Step 2.Consider both evaluation information matrix and expert weights, the fused matrix R=[aij]m×n,i=1,2,…,m,j=1,2,…,n where ωλpresent the weights of dλand can be calculated by Eq. (5); Step 3. Determine the attribute’s weights by Eq. (13)(the attribute’s weights are partly unknown) or Eq. (18)(the attribute’s weights are completely unknown); Step 4.On accordance of the attribute’s weighing vector and the fused results R=[aij]m×n,we can compute the performance results aiof alternatives Ai(i=1,2,…,m) by using q-ROFWA operators. According to deal with the model (M - 3), we can get the optimal solution w = (w1,w2,…,wn)T, which means the attribute weights. Case 2.If the attribute’s weights are completely unknown,then the nonlinear programming model can be constructed as: To solve this model, we construct the Lagrange function: where π is the Lagrange multiplier. Then we differentiate Eq.(22)with respect to wjand π,and the results of partial derivatives are set to zero, then we can obtain following equation; Based on the results of partial derivatives and Eq. (22), we can get the following equation to obtain attribute’s weights. by normalizing Eq. (23), the normalized results are listed as: 4.2.1. The decision-making model 2 Based on maximizing deviation method, the MADM problems with incomplete attribute’s weights under q-RIVOFSs environment can be solved by following steps. Step 1.Construct decision making matrix,i=1,2,…,m,j=1,2,…,n wheremeans assessment information expressed by q-RIVOFNs. Step 2. Consider both evaluation information matrix and expert’s weights, the fused matrixi=1,2,…,m,j=1,2,…,n can be calculated by Eq.(10); Step 3.Determine the attribute’s weighing vector by Eq.(19)(the attribute’s weights are partly unknown) or Eq. (24)(the attribute’s weights are completely unknown); Step 4.On accordance of the attribute’s weighing vector and the fused resultswe can compute the performance resultsalternatives Ai(i=1,2,…,m) by using q-RIVOFWA operators. Step 5.Calculate the score results S(~ai) (i=1,2,…,m)of~ai(i =1,2,…,m),then the ordering of alternative Ai(i=1,2,…,m)can be derived by S(~ai), the bigger S(~ai) is, the better alternative Aiis. Step 6. Order all the alternatives Ai(i=1,2,…,m) based on S(~ai) (i = 1,2,…,m). Step 7. End. Table 1q-ROFNs decision matrix by d1 Table 2q-ROFNs decision matrix by d2 Table 3q-ROFNs decision matrix by d3 In recent years the rapid development of construction industry makes a substantial increase of energy utilization, because the building exterior wall area account for 40%of the total construction area of left and right sides, its importance is obvious, and usually heat preservation and heat insulation energy-saving measures is to strengthen the construction, in building energy-saving wall thermal insulation materials and its detection technology has a significant role in the whole building energy efficiency.In this subsection we shall give a numerical example to show building material identification with q-rung orthopair fuzzy information by utilizing the methods developed in this paper. Given five possible building materials Ai(i=1,2,3,4,5) to select. Three experts (scholars and professors with years of experience in testing building materials and certain knowledge of fuzzy set theory)selects four attribute to evaluate the five possible building materials: ①G1is the apparent density factor; ②G2is the dimensional stability factor; ③G3is tensile strength factor;④G4is the compression strength factor.The five possible building materials Ai(i=1,2,3,4,5) are to be estimated using the q-rung orthopair fuzzy information (Suppose expert’s weights vector is ω =(0.35,0.45,0.20)T),which are shown in Tables 1-3.(Suppose q=3 in this manuscript). Fig.1. The flowchart of q-ROFN decision model. The flowchart of the decision models under q-rung orthopair fuzzy environment can be seen in Fig.1. Case 1. If the attribute’s weighting vector is partly known and given as: Then according to the decision-making model 1 and the q-rung orthopair fuzzy information given in Tables 1-3,we can select the best building material by following steps. Step 2. Consider both evaluation information matrix and expert’s weights, the fused matrix R=[aij]m×n,i=1,2,…,m,j=1,2,…,n can be calculated by q-ROFWA operator and the fused results are listed in Table 4(take a11for example); Thus, the performance results aican be listed as: a1=(0.5874,0.3516),a2=(0.5963,0.3027),a3=(0.6766,0.2742), a4=(0.5772,0.4271),a5=(0.5686,0.2845). Step 5. Calculate the score results S(ai)(i=1,2,…,m) and the results are listed as:S(a1)=0.5553,S(a2)=0.5922,S(a3)=0.6446,S(a4)= 0.5572,S(a5)= 0.5804. Step 6. Order all the building materials Ai(i=1,2,…,m) based on S(ai) (i = 1,2,…,m): A3≻A2≻A5≻A4≻A1.Clearly,A3is the best building material. Step 7. End. Case 2. If the attribute weighting vector is completely known,then according to the decision-making model 1 and the q-rung orthopair fuzzy information given in Tables 1-3, we can develop the best alternatives by following steps. Step 1. Similar to Case 1(Step 1). Step 2. Similar to Case 1(Step 2). Step 3. Determine the attribute’s weighing vector by (M-2), by utilizing Eq. (18), we can derive the attribute’s weight as: w = Step 3.Determine the attribute’s weighting vector by(M-1),the nonlinear programming model can be constructed as: (0.19,0.23,0.26,0.32)T. Step 4. On accordance of the attribute’s weighing vector and by solving this model, we can derive the attribute’s weight as:w = (0.24,0.15,0.39,0.22)T. Step 4. On accordance of the attribute’s weighing vector and Table 4, we can compute the performance results aiof alternatives(take a1for example): Table 4, we can compute the performance resultsaiof alternatives: a1=(0.5825,0.4574),a2=(0.6136,0.3515),a3=(0.6769,0.2838),a4=(0.5981,0.4112),a5=(0.5641,0.2858). Table 4The fused q-ROFNs results by q-ROFWA operators. Table 5Ordering results for differentqby the q-ROFWA operator. Step 5. Calculate the score resultsS(ai)(i=1,2,…,m) and the results are listed as: S(a1)= 0.5510,S(a2)= 0.5938,S(a3)= 0.6436,S(a4)= 0.5722,S(a5)= 0.5781. Step 6.Order all the building material Ai(i=1,2,…,m)based on S(ai) (i = 1,2, …, m):A3≻A2≻A5≻A4≻A1.Clearly,A3is the best building material. Step 7. End. In order to show the effects on the ranking results by changing parameters of q in the q-ROFWA operator,we list the different score results with different parameters, all the results are shown in Table 5. According to Table 5, it’s clear that the ordering results are slightly different for the different parametersqby q-ROFWA operator,and the best alternative isA3.Moreover,we can easily find that the score values become smaller and smaller when the parameterqincreases,but they become more and more steady with bigger parameter, which indicates the decision making results are robust and effective. If the five possible building materialsAi(i=1,2,3,4,5)are to be estimated by q-rung interval-valued orthopair fuzzy information(Suppose expert’s weights isω = (0.35,0.45,0.20)T), which are shown in Tables 6-8. The flowchart of the decision models under q-rung intervalvalued orthopair fuzzy environment can be seen in Fig. 2. Case 1.If the attribute’s weighting vector is partly known and given as: Then according to the decision-making model 2 and the q-rung interval-valued orthopair fuzzy information given in Tables 6-8,we can develop the best alternatives by following steps. Step 1.Construct decision making matrixmeans assessment information expressed by q-RIVOFNs.(See Tables 6-8). Step 2. Consider both evaluation information matrix and expert’s weights,the fused matrix R=[~aij]m×n,i=1,2,…,m,j=1,2,…,n can be calculated by q-RIVOFWA operators and the fusedresults are listed in Table 9; Table 6q-RIVOFNs decision matrix by.d1 Table 7q-RIVOFNs decision matrix by.d2 Table 8q-RIVOFNs decision matrix by.d3 Fig. 2. The flowchart of q-RIVOFN decision model. Step 3.Determine the attribute’s weighing vector by(M-3),the nonlinear programming model can be constructed as: by solving this model, we can derive the attribute’s weight as:w = (0.28,0.30,0.20,0.22)T. Step 4. On accordance of the attribute’s weighing vector and Table 9, we can compute the performance results~aiof alternatives: Step 5. Calculate the score resultsS(~ai) (i=1,2,…,m) and the results are listed as:S(~a1) =0.5954,S(~a2) =0.5704,S(~a3) =0.6917,S(~a4) = 0.5695,S(~a5) = 0.5393. Step 6.Order all the building material Ai(i=1,2,…,m)based on S(~ai) (i = 1,2, …, m): A3≻A1≻A2≻A4≻A5.Clearly,A3is the best building material. Step 7. End. Case 2.If the attribute weighting vector is completely known,then according to the decision-making model 2 and the q-rung interval-valued orthopair fuzzy information given in Tables 6-8,we can develop the best alternatives by following steps. Step 1. Similar to Case 1(Step 1). Step 2. Similar to Case 1(Step 2). Step 3. Determine the attribute’s weighing vector by (M-4), by utilizing Eq. (24), we can derive the attribute’s weight as: w=(0.28,0.30,0.16,0.26)T. Table 9The fused q-RIVOFNs results by q-RIVOFWA operators. Table 10Ordering results for different q by the q-RIVOFWA operator. Step 4. On accordance of the attribute’s weighing vector and Table 9,we can compute the performance results~aiof alternatives: Step 5. Calculate the score results S(~ai) (i=1,2,…,m) and the results are listed as: S(~a1) = 0.5997, S(~a2) = 0.5753, S(~a3) =0.6914,S(~a4) = 0.5717,S(~a5) = 0.5352. Step 6.Order all the building material Ai(i=1,2,…,m)based on S(~ai) (i = 1,2,…,m): A3≻A1≻A2≻A4≻A5.Clearly, A3is the best building material. Step 7. End. In order to show the effects on the ranking results by changing parameters of q in the q-RIVOFWA operator, we list the different score results with different parameters,all the results are shown in Table 10. According to Table 10, it’s clear that the ordering results are slightly different for the different parameters q by q-RIVOFWA operator,and the best alternative is A3.Moreover,we can easily find that the score values become smaller and smaller when the parameter q increases, but they become more and more steady with bigger parameter,which indicates the decision making results are robust and effective. From above analysis, we can easily find that our presented maximizing deviation methods under q-rung orthopair fuzzy environment and q-rung interval-valued orthopair fuzzy environment are more reasonable and convenient to deal with practical MADM applications. The reason is that our established model can not only deal with real applications with incomplete information but also the indeterminate information. Therefore, our paper extends the existing decision-making methods and proposes a new tool for decision maker (DM). In addition,compare our proposed methods with other decision making tool such as weighted average (WA) operator, Bonferroni mean (BM) [44-46] operator, Heronian mean (HM) [48-50]operator, Hamy mean (HM) [55,56] operator and Maclaurin symmetric mean (MSM) [41-43] operator, all above methods can handle MADM problems with q-rung orthopair fuzzy information and select the best alternatives by score results,but when we utilize these mentioned methods, the DM’s and attribute’s weights need to be completely known, at the same time,the process of decision making is up to only a decision-maker. However, due to the complex environment and the subjectivity of the decision maker, the decision making process is always uncertain and the weights information is partly known or completely unknown. Obviously,when we face with such issues,the maximizing deviation methods under q-rung orthopair fuzzy environment developed in this paper can be more valid to deal with MADM applications.Furthermore,to obtain more accuracy and effective decision making results, the evaluation information is given by three DMs in this paper rather than only a DM in other existing literature. On the basis of above analysis,the q-rung orthopair fuzzy set(q-ROFS) is characteristic of the degree of membership and nonmembership which satisfies the q-th power of them are limited to 1. By comparing with intuitionistic fuzzy set (IFS) and Pythagorean fuzzy set(PFS),it’s clear that both two above fuzzy sets are the special case of q-ROFS;it means that q-rung orthopair fuzzy set(q-ROFS) can express more fuzzy information and solve the MADM problems which IFS and PFS can’t deal with. In other words, the maximizing deviation methods with q-rung orthopair fuzzy information also can be applied in MADM problems with intuitionistic fuzzy information and Pythagorean fuzzy information. Therefore,above mentioned comparison shows that our proposed method have the advantage of dealing with more complex and uncertain MADM problems with q-rung orthopair fuzzy information. As the generalization of IFS and PFS,the q-ROFS can depict more fuzzy information which indicates the q-ROFS can be more suitable for handling actual decision making applications. Due to the complex and uncertainty of the environment,the weights of DM’s and attributes are always partly known or completely unknown, to conquer this limitation, the maximizing deviation method is proposed to solve such MADM problems. Combine the q-ROFS and conventional maximizing deviation method,in this paper,we study the MADM problems with q-ROFNs and q-RIVOFNs. According to the basic concepts of q-ROFSs, q-RIVOFSs and traditional maximizing deviation method, we construct two new decision making models. Moreover, we have adopted our proposed new models to solve the MADM problems with q-rung orthopair fuzzy information. Finally, an example is given to evaluate the selection of building materials, which verifies the correctness and scientific of the defined model. It’s clear that our developed methods have the advantages of handling the MADM problems with incomplete attribute weights and extending the scope of assessment information. However, the newly defined models can derive more accuracy decision making results, but it’s difficult to collect related decision making data for lacking experts with both fuzzy theory and architectural background.Thus,it’s important to overcome this limitation in the following study.In the future,we will continue to study the MADM problem [66-73], and apply the developed method to construction project selection, Supply chain management and many other fields to derive more scientific and reasonable decision making results[74-82]. Declaration of competing interest The authors declare that they have no conflict of interest. Acknowledgment The work was supported by the National Natural Science Foundation of China under Grant No.71571128 and the Humanities and Social Sciences Foundation of Ministry of Education of the People’s Republic of China (No.17XJA630003).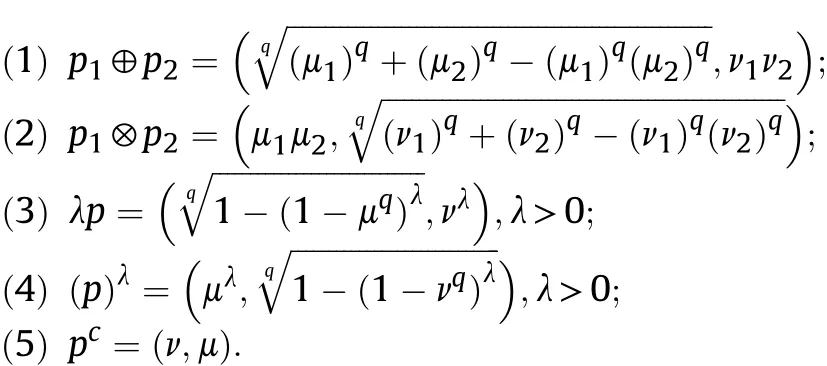

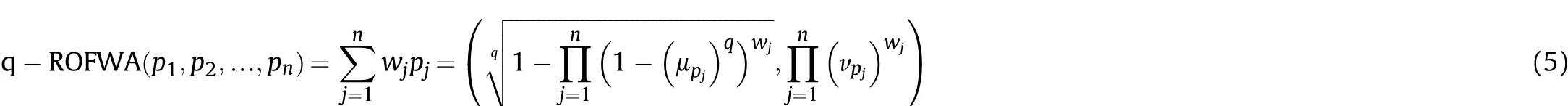
3.2. The q-rung interval-valued orthopair fuzzy set

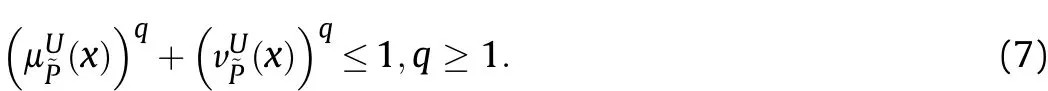
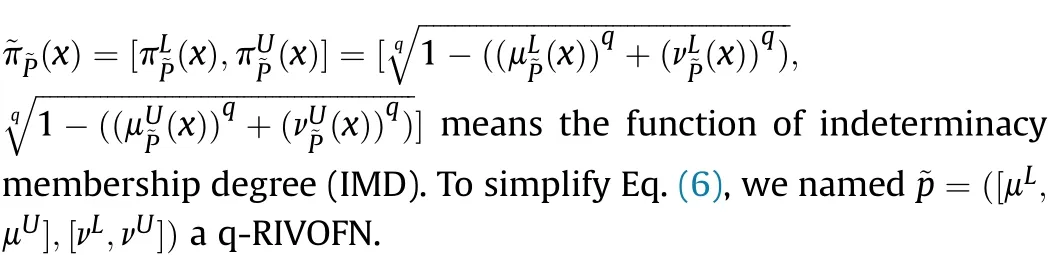
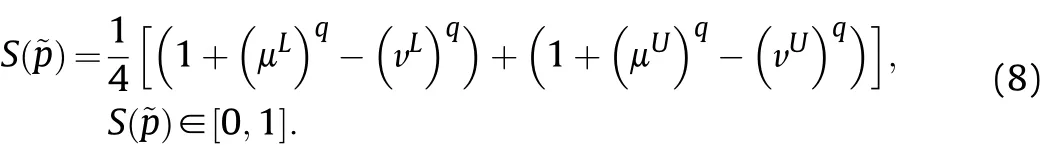
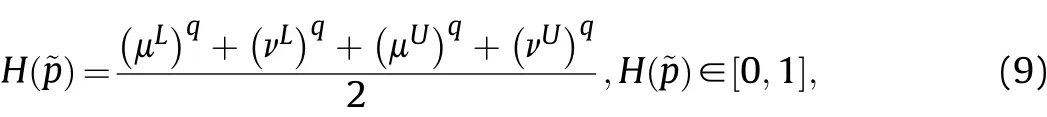

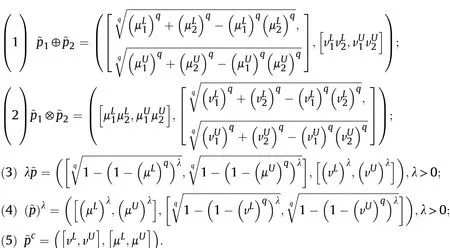
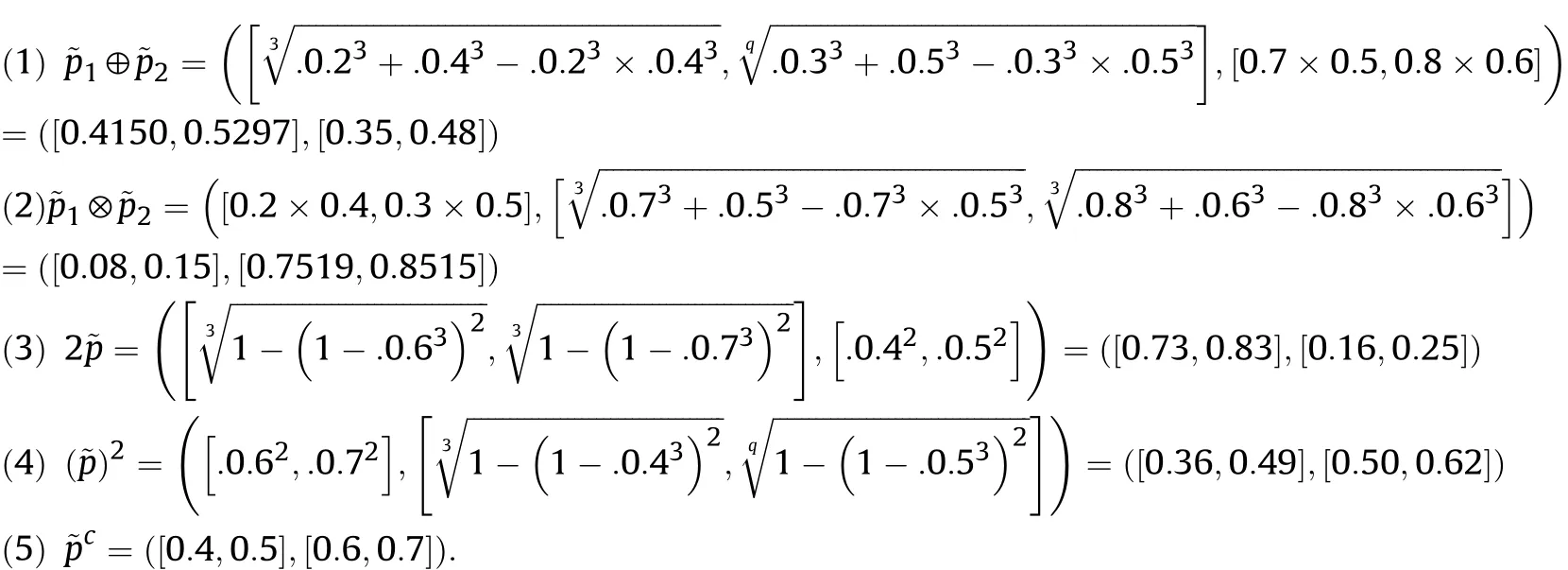

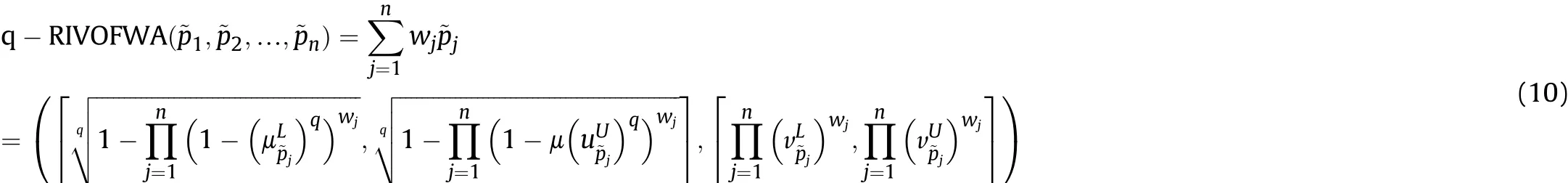
4. Maximizing deviation method for q-ROFNs information
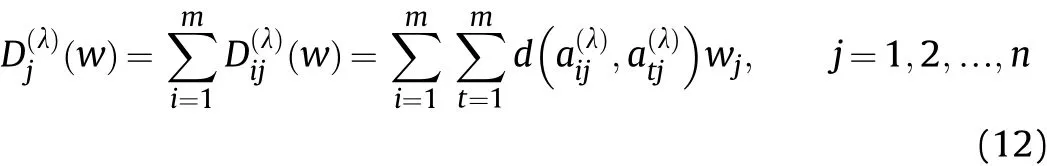
4.1. Maximizing deviation method for q-rung orthopair fuzzy set
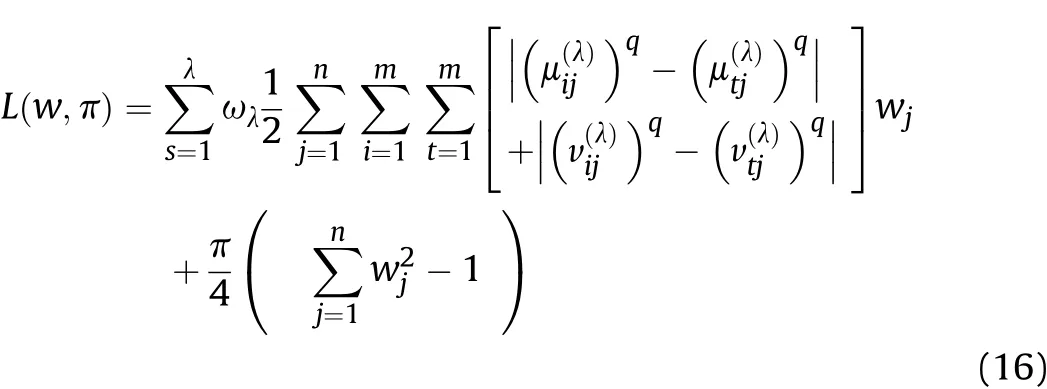
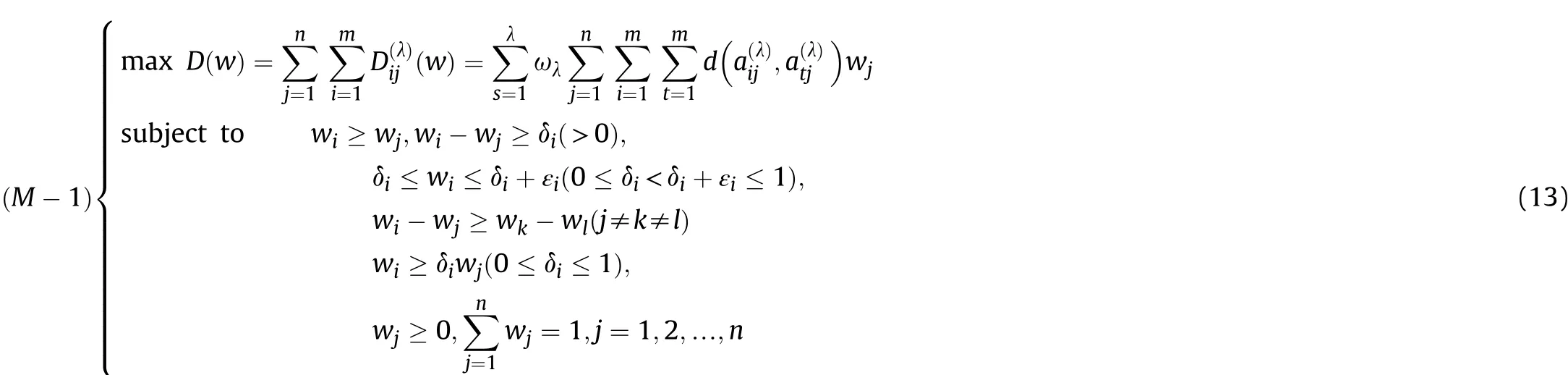
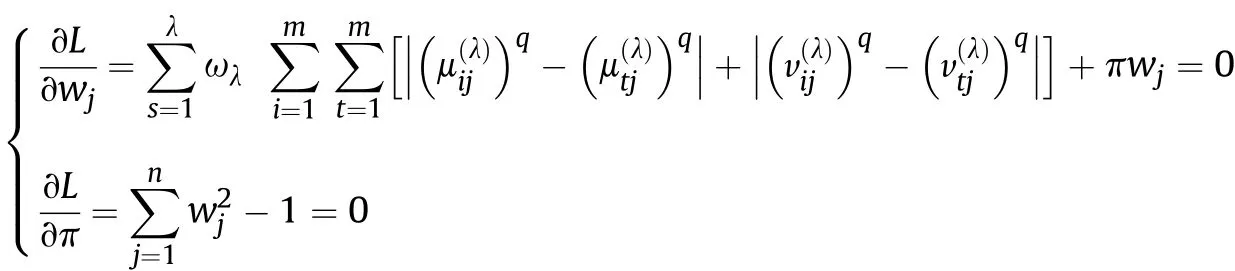
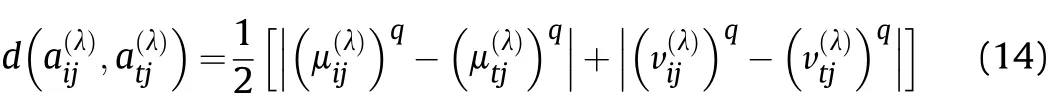
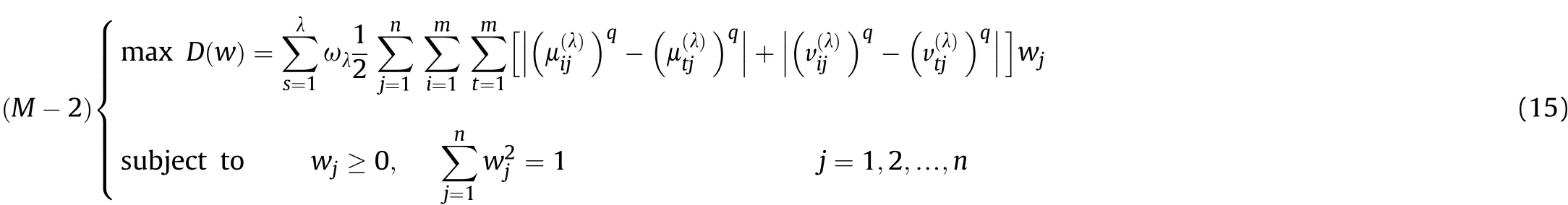
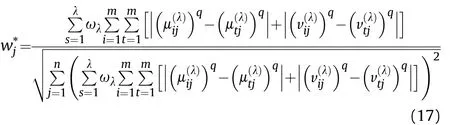
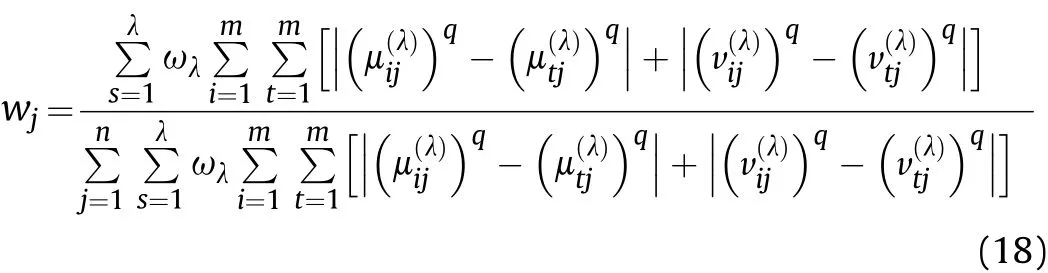
4.2. Maximizing deviation method for q-RIVOFSs

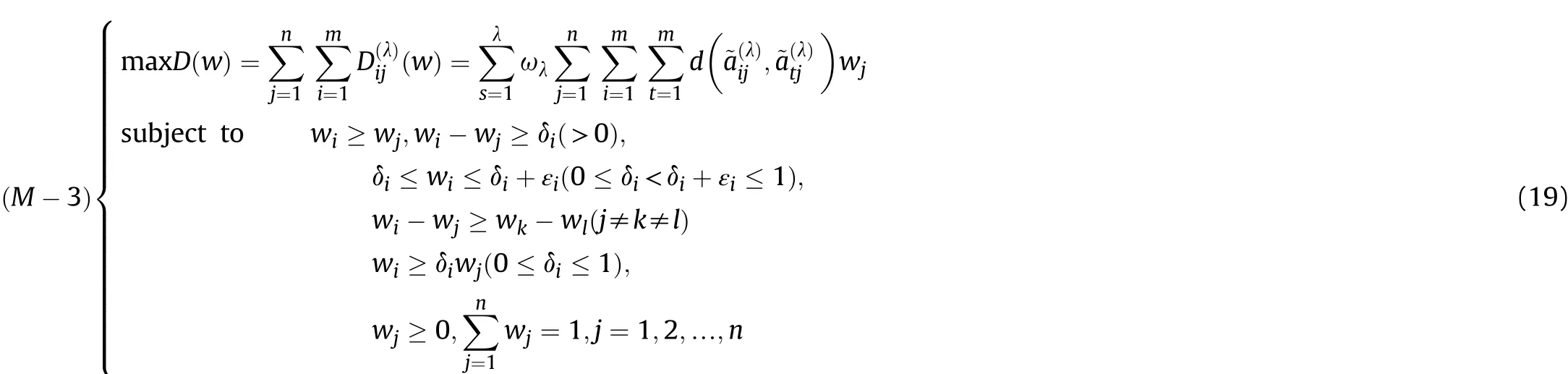
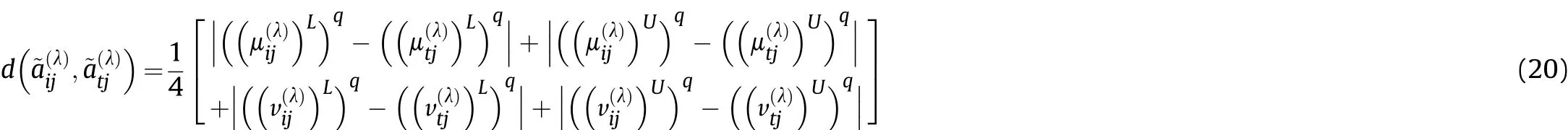
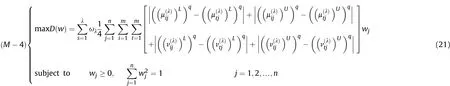
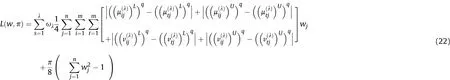
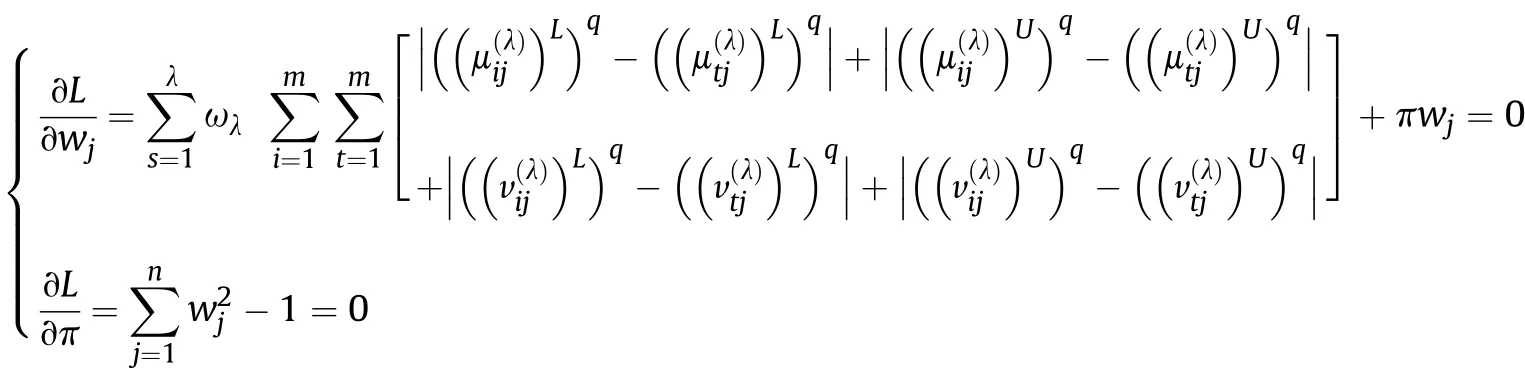
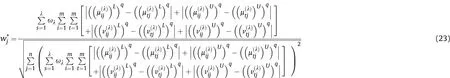
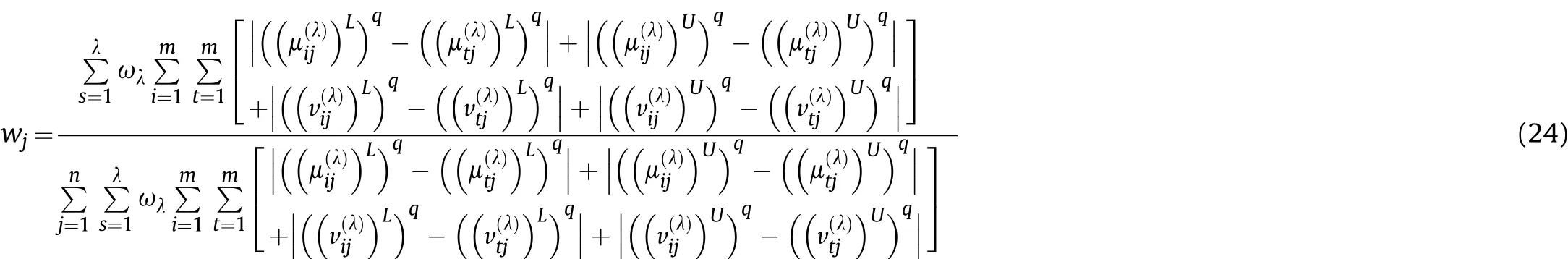
5. Numerical example and comparative analysis
5.1. Numerical Example 1
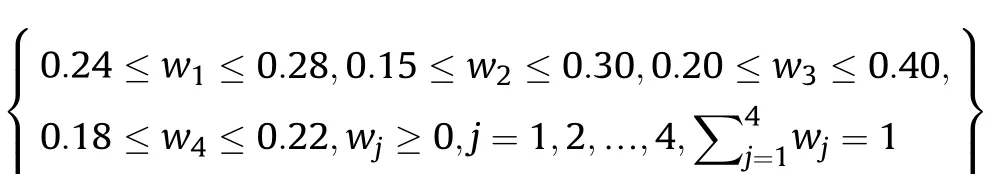
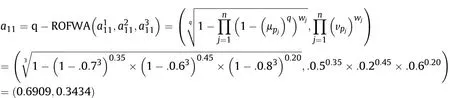
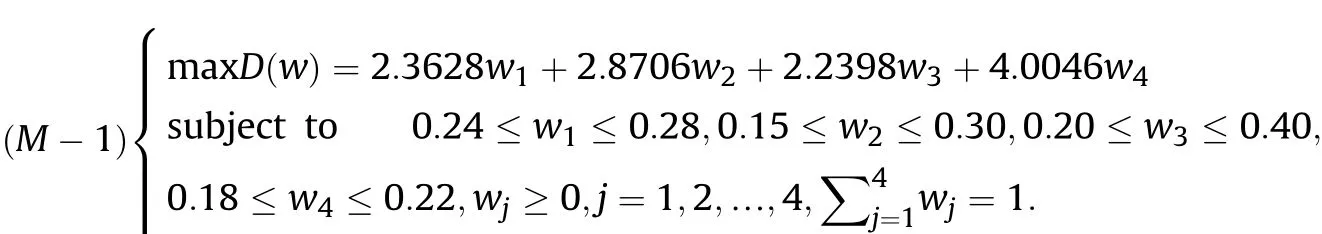
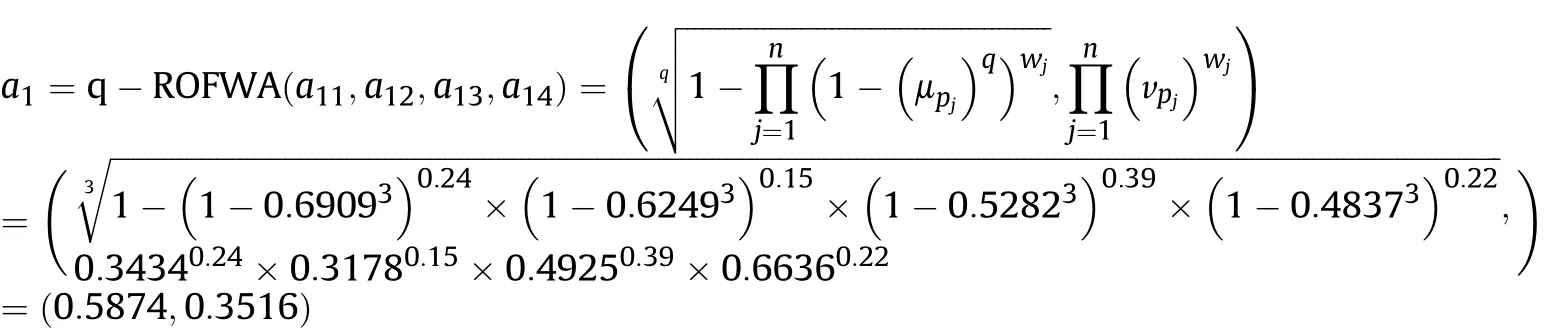
5.2. Influence of the parameterqwith q-ROFNs
5.3. Numerical Example 2
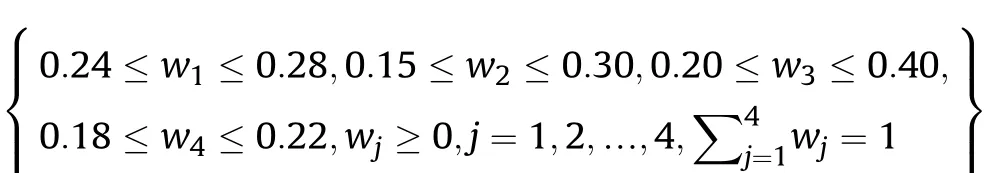




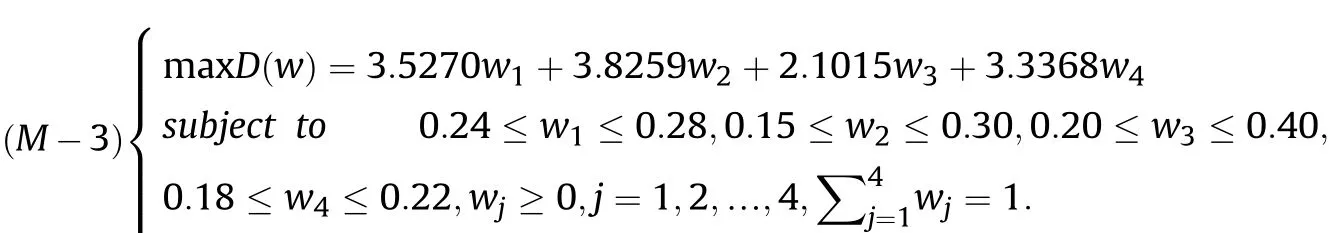

5.4. Influence of the parameter q with q-RIVOFNs
5.5. Comparative analysis
6. Conclusion
- Defence Technology的其它文章
- Analysis of the stress wave and rarefaction wave produced by hypervelocity impact of sphere onto thin plate
- Effect of bending temperatures on the microstructure and springback of a TRIP steel sheet
- Dynamic parameters of multi-cabin protective structure subjected to low-impact load - Numerical and experimental investigations
- An eikonal equation based path planning method using polygon decomposition and curve evolution
- Influence of active constrained layer damping on the coupled vibration response of functionally graded magneto-electro-elastic plates with skewed edges
- Consequence of reinforced SiC particles and post process artificial ageing on microstructure and mechanical properties of friction stir processed AA7075

