电网阻抗对光伏电站谐波过电压的影响

赵鹏程

（黄河水电物资有限公司，青海 西宁 810003）

0 引 言

近年来，太阳能发电技术发展迅速，成本下降，全球范围内大规模的光伏应用使光伏发电成为最具有发展前景的发电技术[1]。光伏发电安全可靠，不需要额外的燃料消耗，无污染，维护简单，受地域限制较小，可大规模集中发电，也适宜分散发电。光伏发电主要包括分布式光伏发电和太阳能热电发电，我国主要采用光伏发电[2]直接将光能转化为电能[3]。

本文基于光伏电站无源网络模型，分析了逆变器的输出导纳特性，并依据实例从时域、频域分别分析电网阻抗对光伏电站谐波过电压的影响。

1 光伏电站无源网络模型

本文选择青海乌兰某光伏电站的拓扑，推导其无源网络模型。光伏电站采用两级升压模式，光伏发电单元经一级升压变后汇集到10 kV母线开关，10 kV母线接入主变压器（1#主变容量为31.5 MVA），低压侧升压至110 kV，并由110 kV线路送至330 kV变110 kV侧，接线形式为单母线接线。为了使得到的结果具有通用性，推导过程中，光伏单元数使用参数n描述，集电线路用m描述。光伏电站结构如图1所示。

依据前文所述进行等效，可得到光伏电站与集电线路等效阻抗图，其中，集电线路等效阻抗图如图2所示。

图2中，ZN为逆变器及其LCL滤波器等效阻抗；Zt1、Zt2、Zt3分别为双分裂变压器的原边绕组及两个副边绕组的等效阻抗；Zdi和Ydi（i=1,2…,n）分别为单条集电线路的第i个发电单元后连接的电缆线路的等效阻抗和导纳；ZT和YT分别为光伏电站升压变压器的等效阻抗和导纳；ZS为该光伏电站并入的大电网的等效阻抗。

谐波传递拓扑的节点导纳矩阵Y是一个4mn+2阶的方阵。

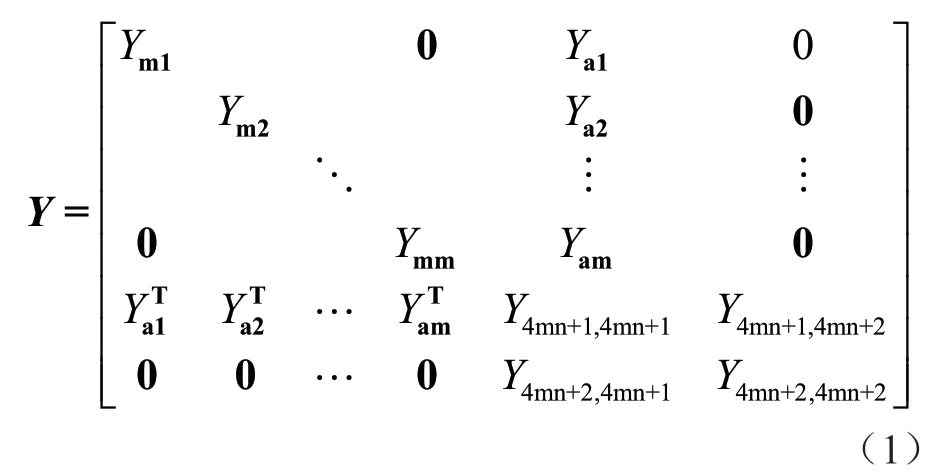
其中：Yai为4n×1阶列向量。

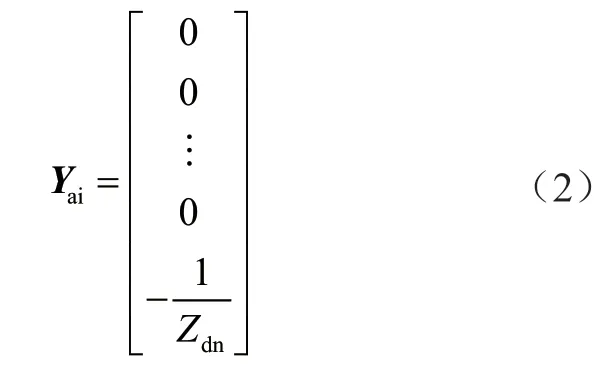
式中：Zdn为每条集电线路的最末端一段电缆。

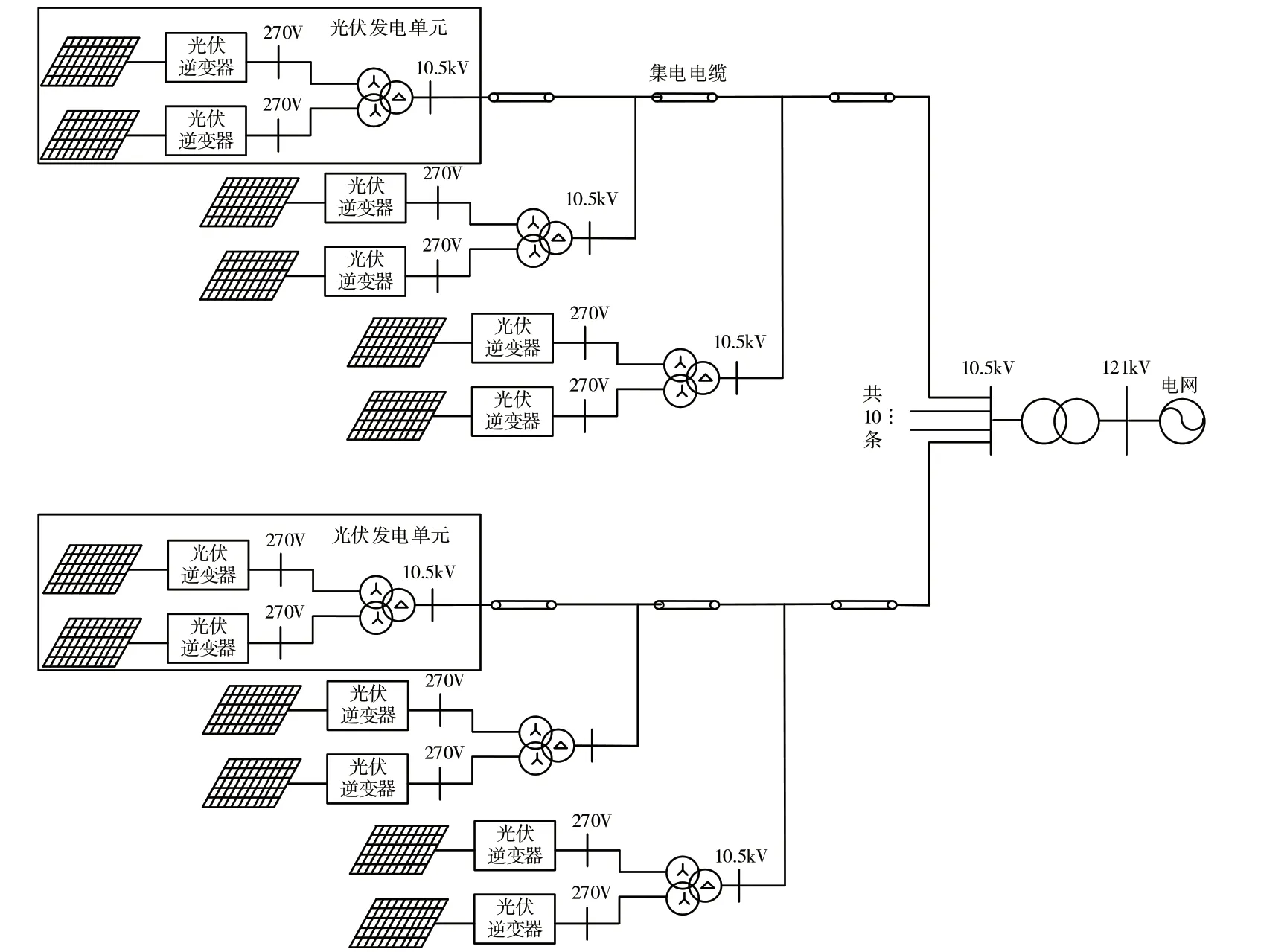
图1 青海乌兰某30 MW光伏电站拓扑结构图

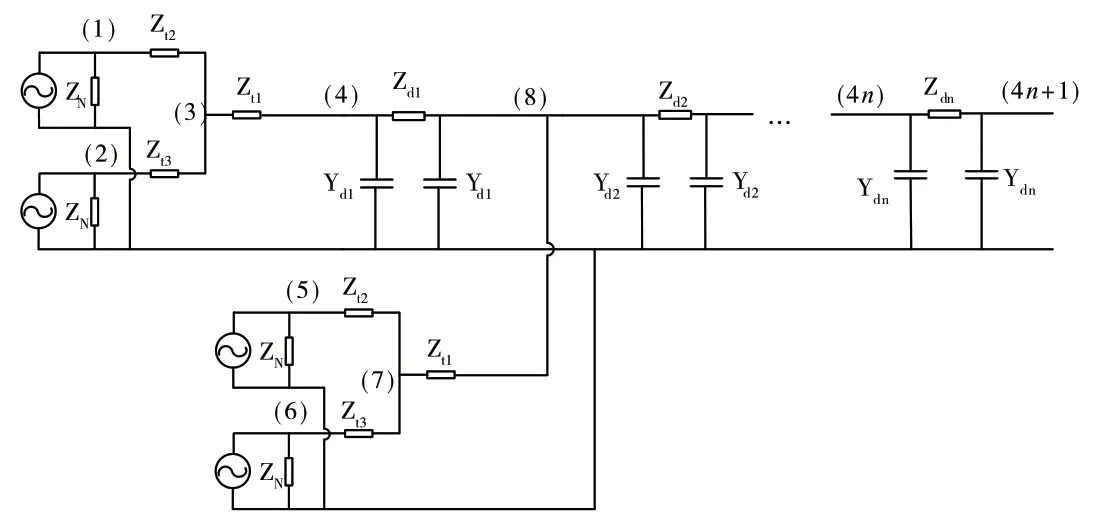
图2 集电线路等效阻抗图

Ymi(i=1,2…,m)为第i条集电线路的节点导纳矩阵，其为4n阶方阵，则：

式中，Y1、Y2为4阶方阵，其中，方阵Y1为整个支路中第一发电拓扑节点及与本节点有关电缆的导纳矩阵总集，Y2为整个支路除第一发电拓扑节点外的发电节点和跟这些发电拓扑节点相关联的电缆的导纳矩阵总集。为了正确得到举证Ym，这里将定义Yb的补充矩阵为矩阵Yc。可得：

方阵Yi(i= 2,3…m)除Yi(4,4)的位置的值与方阵Y1一式一样，集电网络单支路第i个(i= 2,3…n)发电网络的节点导纳矩阵Yi为：

Yc为4n阶对称方阵，有

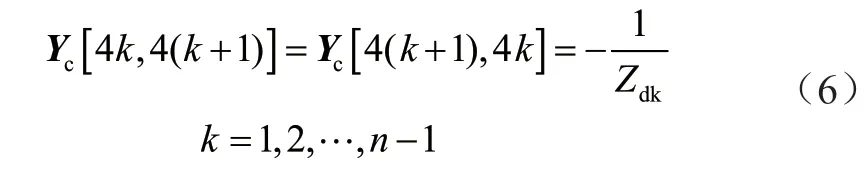
本文谐波潮流的计算方法与基波潮流计算方法如出一辙，通过由谐波传递所对应的节点Y导纳矩阵和与谐波源的每个节点相对应的谐波电流勾出潮流方程，因此，用所述网络的方程式来总结每个节点的谐波电压为：

式（7）中，网络中各个节点h次谐波电压列向量为U(h)；各节点h次谐波注入电流列向量为I(h)；Z(h)为h次谐波传递网络的节点阻抗矩阵：

式中，Y(h)为h次谐波传递网络的节点导纳矩阵。

2 光伏电站谐波过电压与电网阻抗之间的关系

2.1 光伏电站谐波含量与电网阻抗的联系

为了找到光伏电站谐振现象是否与电网阻抗有关，分析谐波网络传递函数带宽的限制因素中的电网阻抗，对电网阻抗和系统谐波含量之间相互影响关系进行分析，讨论系统稳定性是否受电网阻抗的影响以及受何种影响，逐步深入分析光伏电站谐波谐振现象。结合第1部分适用于谐波谐振研究的光伏电站无源网络模型分析，将上述建模方法用于所有并联逆变器，可以将光伏电站等效为诺顿模型。运用诺顿定理使分裂变压器等效电感、光伏逆变器的等效电路进行等效变换。图3为简化后进行的光伏电站等效电路。

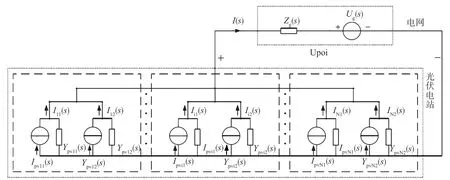
图3 光伏发电二端口网络等值简化结构

图3中，Ipvi1(s)和Ypvi1(s)为光伏发电站中第i个单元网络中逆变器的等效参考电流和等效简化导纳，可表示为：

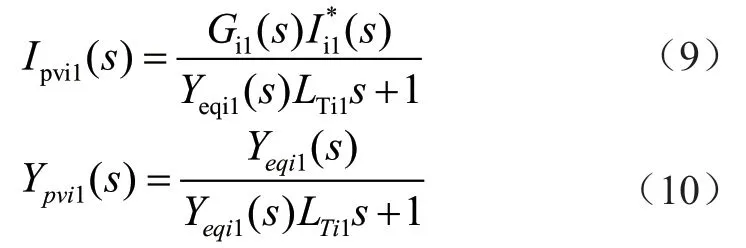
从图3中可以看出，光伏发电系统利用电网阻抗之间的耦合和分裂变压器等效电感，使得该系统的所有并联逆变器之间以及该系统和电网之间存在相互作用。第i个单元模块中逆变器j的并网电流可通过叠加原理推导出公式（11）：

在此推导公式中，电网的导纳可表示为：

本文将采用扰动量为公式（13）：

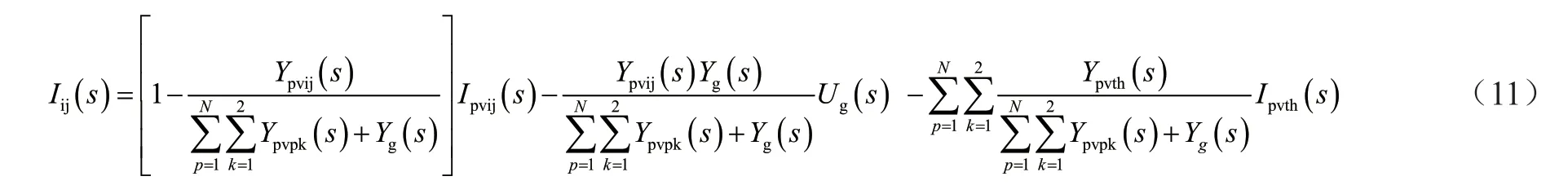
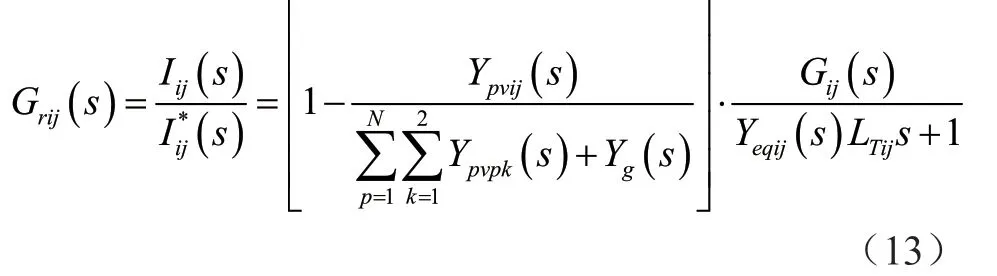
通常在光伏发电系统中采用的逆变器拓扑和逆变器闭环控制方法相同，本文对各个逆变器提出一些假设。假设各项参数和指标以及逆变器的控制策略一毫不差时，式（13）可以简化为：

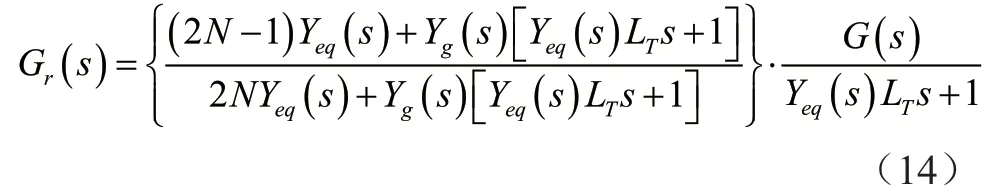
想要使电网阻抗影响网络的传递函数谐振频率观察得更加主观、清晰，在用软件进行仿真和实际验证过程中使用了Bode图来分析，由式（14）得出开环传递函数中存在系统传递函数特性的影响因素。

将供电系统的阻抗加入光能并网逆变器，发电系统中传输电流相对应的函数对数频特性仅包含谐振峰，该谐振峰是存在于谐振频率处的。光能发电厂多个逆变器的并联连接，存在两个共振峰。从具有定频率的谐振峰到另一个谐振峰的谐振频率会根据系统阻抗和光能发电厂的功率的变化而变化。Gr(s)的带宽和谐振频率会受到电力网络阻抗中等效电感L的影响，会随L的上升而下降。电网增加等效电阻会提高抗谐振性能，并抑制谐振峰值，进而提高整个系统的动态稳定性。电网等效阻抗的其中一影响因素为发电单元的容量V，其大小会随V的增大而增大。当V增大时，Gr(s)的带宽和系统的谐振频率会随V的增大而减小。与此同时，系统加强了抗共振峰的力度，并且系统的稳定性随之提高。

为方便对上述结论进行验证，在青海中广核乌兰光伏电站的参数及选型的基础上，对部分参数进行适当整定，以更好地适应就电网阻抗对光伏电站谐波谐振影响的分析。由于光伏电站采用的逆变器均为同一型号，各发电单元的外特性大致相同，因集电线路长短不同带来的影响予以忽略，因此可选择任一逆变器作为研究对象。

当光发电系统中逆变器并网时谐波电流的THD为1.92%时，相对应的电力网络中阻抗等效电阻RL和等效电感L分别为3.2 mΩ和19.5 μH；当THD变换为1.84%时，相对应的RL和L分别为3.2 mΩ和23.3 μH，此时，对应的光发电并网系统谐振频率为1 470 Hz和1 550 Hz；当THD变换为2.19%时，相对应的RL和L分别为4.81 mΩ和23.3 μH，此时，对应的光发电并网系统谐振频率为1 450 Hz和1 550 Hz；当THD由1.92%减小为1.84%时，相对应的L从19.5 μH提升到23.3 μH，此时，谐振频率由1 470 Hz变换为1 450 Hz。

2.2 并网阻抗对光伏电站稳定运行的影响

光伏电站中，如果电力网络的阻抗增加，则系统可能会谐振，从而导致整个系统不稳定。因此，必须分析整个系统稳定运行条件下的区域。以两个级联子系统的阻抗比是否满足标准Nyquist稳定性来确定级联系统的稳定性。采用阻抗稳定性判据非常适合确定级联系统的稳定性，确定的结果取决于子系统阻抗的实际测量，因此是可靠的、值得信赖的。所以，通过仿真验证了系统的稳定运行，验证了分流结果，为抑制光伏电站谐振和所产生的谐波的策略提供了指导和参考。

实际中，为了判定系统的稳定性，可通过测量光能发电系统和两个级联子系统阻抗，利用Nyquist判据判断光伏电站最小环路增益是否包围(-1,j0)点，从而判定系统稳定性。

3 结 论

本文推导了光伏逆变器的诺顿模型，分析逆变器的输出导纳特性，评估其导纳可能的取值范围，并以青海乌兰某光伏电站拓扑为例，推导出适用于谐波过电压分析的无源网络模型。结合模型明确了电网阻抗对光伏电站谐波过电压的影响，分别从时域和频域角度，对其进行研究。