基于时间相依Cox回归的动态财务预警模型及实证
李鸿禧, 宋 宇
(1.中央国债登记结算有限责任公司 博士后科研工作站,北京 100033; 2.中国人民银行 金融研究所博士后流动站,北京 100800; 3.中国东方资产管理股份有限公司 博士后科研工作站,北京 100034; 4.清华大学 经济管理学院博士后流动站,北京 100084)
0 引言
财务预警是通过挖掘企业数据和财务风险之间的关联关系,预测企业发生财务危机的概率。对企业财务风险进行监控预警,一方面能够提前给出风险信号,便于企业管理者及早改善经营,避免破产违约事件的发生。另一方面,能够为银行、基金等机构进行投资提供决策参考,避免信用风险给投资者带来的巨额损失。
财务预警模型的现有研究大致可分为三类:
一是基于统计计量方法,代表性的有判别分析、聚类、逻辑回归等方法。鲍新中利用粒子群的K均值聚类算法将企业的财务风险分成了四类,得到每个企业的综合财务得分[1]。顾海峰基于偏好信息熵和物元可拓理论,对信用突变下商业银行信用风险进行预警[2]。谢赤等利用CfaR模型识别期望现金流,并以此作为预警变量构建二元Logistic财务困境预警模型[3]。孙晓琳基于状态空间模型构建财务危机的动态预警模型,计算出模型的时变参数[4]。方匡南等利用网络机构Logistic模型,通过惩罚方法同时实现变量选择和参数估计,从而构建企业信用风险预警模型[5]。Fabio Comelli对比了逻辑回归和probit模型的精度,构建新兴市场上的财务危机预警模型[6]。Babecky J等利用面板矢量自回归模型,研究了银行、债务危机以及货币危机之间的关系,建立了危机预警模型[7]。
二是基于机器学习方法,代表性的有决策树、支持向量机、神经网络、贝叶斯估计等。鲍新中等将公司财务状况分为5个等级,先后利用变精度加权平均粗糙度决策树方法、神经网络方法建立财务预警模型[8,9]。黄超等利用主成分分析和支持向量机的方法,构建企业财务危机预警模型[10]。叶焕倬等采用自适应贝叶斯网络模型进行财务危机预警和危机原因诊断[11]。吴冲等利用粒子群算法优化了概率神经网络平滑参数,构建企业财务危机预警模型[12]。Koyuncugil A S等利用CHAID决策树算法,以土耳其银行的中小企业为实证样本,构建财务风险预警模型[13]。Sevim C等利用决策树、神经网络、逻辑回归三种模型建立一个预测货币危机的预警系统[14]。
三是基于多种方法的集成,将多个预警模型的结果融合在一起,形成一个最终的预警结果。张亮等在支持向量机和逻辑回归模型的基础上利用信息融合方法构建财务预警模型,解决不同挖掘方法得到结果不一致的问题[15]。符刚等利用全局主成分分析法,构建了融合神经网络与卡尔曼滤波法的财务风险预警模型[16]。Javier De Andrés等将模糊聚类和多元自适应回归模型结合起来,对企业的破产概率进行预测[17]。Chen M Y基于决策树和逻辑回归的对比遴选最优的模型,构建公司财务状况的预警模型[18]。
Cox模型是在1972年由Cox提出的一种半参数生存分析模型[19],最早用于生物医学研究,近些年来被引入到企业财务危机预测中。相比于现有大多预警研究仅预测某一个时间点上危机概率,Cox回归模型的优点在于可以得到未来一段时间内动态的预警结果,而且对于自变量没有假设分布的限制。鲍新中等利用变量聚类和Cox回归的方法,构建A股上市的制造业企业财务预警模型[20]。卢永艳利用Cox回归模型分析行业差异对于上市公司财务困境风险的影响[21]。
上述基于Cox回归的财务预警模型,均是采用固定协变量的Cox模型,即通过某一期的预警指标数据(协变量)来预测未来一段时间的危机概率。然而事实上,包括企业的财务指标、外部的宏观指标等因素均是随着时间而变化的面板数据,若仅用一期的截面数据建模,涵盖的数据不足以覆盖历史数据的变动,必然导致预警结果不够准确。故本研究采用时间相依的Cox回归模型[22],即预警指标(协变量)是随时间而变化的面板数据,考虑了企业信息、外部影响等因素在时间维度上的变化,涵盖了更多的历史信息,达到提高预警精度的目的。
1 动态财务预警模型的构建
1.1 基于共线性检验的冗余指标剔除
预警模型中指标过多、指标之间存在较高的共线性,会造成信息冗余重复,影响模型的判别精度。所以首先要对冗余指标进行剔除。
共线性检验是通过构建指标之间的线性回归方程,利用回归方程的方差膨胀因子VIFj,检验一个指标可以被其它指标线性替代的程度,删除共线性程度大的指标,达到剔除冗余信息的目的。
(1)构建指标之间的线性回归方程
以任意一个指标Zj作为检验变量。以指标Zj为因变量,以其他指标为自变量构建线性回归方程,其中a0,a1,…,am-回归方程的待估参数,则[23]:
Zj=a0+a1Z1+…+aj-1Zj-1+aj+1Zj+1+…+amZm
(1)
通过最小二乘法对回归方程进行参数估计。
对式(1)进行拟合后得到指标Zj的估计值,计算回归方程的可决系数[23]:
(2)

(3)计算方差膨胀因子VIF
(3)

将海选指标体系中每一个指标都作为检验变量,重复上述过程,计算每个指标的方差膨胀因子,删除方差膨胀因子VIFj大于10的冗余指标,避免信息反映重复。
1.2 基于时间相依Cox模型的财务危险强度拟合
1.2.1 基本模型
Cox模型研究危险因子(协变量)与生存时间之间的关联关系。时间相依Cox模型是含时间相依协变量的Cox回归模型、也称扩展Cox模型。一般的Cox模型中协变量是固定的、不随时间而变化;而时间相依Cox模型考虑了协变量随时间的动态变化,可以对协变量为面板数据的情况进行分析。在财务预警模型中,评价因素多为企业的财务指标,例如资产负债率、ROE等,这些指标均是随时间而变化的。所以,利用时间相依Cox模型更能刻画企业财务因素的动态变化对于财务危机的影响。
生存时间T是时间起点到终点之间的时间,终点是感兴趣事件的发生或者是观测期结束。由于本文研究的是财务危机预警,我们关心的是企业何时发生财务危机。那么,对于发生财务危机的企业,生存时间是从上市日到财务困境发生的时间。对于正常健康的企业,生存时间是从上市日到观察期结束的时间。
时间相依Cox回归模型中:左端是因变量危险强度h(t),反映在时刻t时发生财务困境的瞬时概率。在实证样本拟合时,右端h(t)代入的是“实际危险状态(发生财务危机即为1、否则为0)”与“生存时间T”的比值,表示样本企业发生财务危机的平均强度。右端是两个部分因素的乘积,一是随时间推移而变化的基准危险强度h0(t),反映由于时间而累积的财务风险。二是与企业自身经营管理相关的风险因素exp[β1Z1(t)+βqZq(t)]。其中,βi是回归系数,Zk(t)是企业在t时刻的各评价指标数据、也协变量。则[19]:
h(t)=h0(t)exp[β1Z1(t)+β2Z2(t)+…+βqZq(t)]
(4)
式(4)中,h0(t)是基于Breslow估计量进行估计,详见下文式(5)。βi是基于极大似然估计得到,详见下文式(6)。
由指数函数性质,式(4)中指标Zk(t)每增加一个单位,相应地财务危险强度h(t)会变化exp(βk)倍。因此,可以根据回归系数βk的正负判断指标的风险属性,判断标准如下:
①数值越大企业财务风险越低的指标称为保护因素:当回归系数βk<0,说明指标Zk(t)每增加一个单位,财务危险强度h(t)变化exp(βk)倍,exp(βk)在0和1之间,故企业的财务风险变低了,则回归系数βk<0的指标为保护因素。
②数值越大企业财务风险越高的指标称为危险因素:当回归系数βk>0,说明指标Zk(t)每增加一个单位,财务危险强度h(t)变化exp(βk)倍,exp(βk)大于1,故企业的财务风险变高了,则回归系数βk>0的指标为危险因素。
式(4)即为基于时间相依Cox回归的财务危险强度拟合模型,相比于一般的Cox回归模型。其特色在于模型中的协变量数据Zk(t)是随时间变化的面板数据,而非某一时刻的固定值,反映在各个时间上自身财务因素、非财务因素、外部宏观因素的变化对于企业发生财务危机的影响,能够对财务危机进行动态预测。
1.2.2 参数拟合
Cox回归模型中基准危险强度h0(t)是利用Breslow估计量对基准危险强度h0(t)进行估计。设:t1 式(5)的含义:在危险时刻ti上基准危险强度为发生危机的企业个数与该时刻存活企业风险因素总和的比值。在非危险时刻上基准危险强度为0。 Cox回归中回归参数βi是通过极大似然估计的方法进行估计的。构建似然函数[22]: (6) 在似然函数式(6)最大值时,求得的系数βi为最终的回归系数拟合结果。 根据生存分析模型,生存概率S(T)定义为生存时间大于等于T的概率,危险概率F(T)定义为生存时间小于T的概率,危险强度h(t)定义为在时刻t时发生财务困境的瞬时概率,有如下关系[19]: (7) F(T)=Pr(t≤T)=1-S(T) (8) 本研究利用时间相依Cox回归模型拟合危险强度函数h(t),然后利用式(7)和式(8)求解企业健康经营的生存概率S(T)和发生财务危机的危险概率F(T)。根据生存概率S(T)的大小,与危险阈值的对比关系,对企业进行财务危机预警。 在利用时间相依Cox回归模型进行风险预警时,必须先确定一个阈值K。当一个企业的生存概率S(T)小于阈值K时,将该企业判定为财务危机企业,发出财务预警;反之,判定为健康企业。因此,阈值K是财务预警模型中的重要参数,关系到模型精度的高低。而现有研究利用Cox回归模型时较少涉及到判别阈值的确定。 本文采用反推的思路,以判别错误成本最低为目标反推一个最优的阈值K。由于第一类错误“将财务危机企业错判为健康企业”给投资者带来的伤害要大于第二类错误“将健康企业误判成财务危机企业”,故在错误率的基础上考虑了不同错误带来的损失程度、即“成本”,从而构造了判别错误成本。通过遍历法找到判别错误成本最低的预警阈值。具体步骤如下。 Step1选取任意一个样本的生存概率Sj(T)作为阈值K。利用该阈值K对全部样本判定“是否为财务困境企业”。 Step2将Step1的判定结果与真实的财务状态进行比较,得到四个指标:“实际困境企业被判为困境企业的个数a”、“实际困境企业被判为健康企业的个数b”、“实际健康企业被判为困境企业的个数c”、“实际健康企业被判为健康企业的个数d”。 Step3构造错误成本。第一类错误“实际困境企业被判为健康企业”给投资人造成的损失要大于第二错误“实际健康企业被判为困境企业”。应该对第一类错误赋予更大的权重w(w>1)。则错误成本r: r=wb/(a+b)+c/(c+d) (9) 本研究中将权重w设置为3,表示第一类错误与第二类错误的错误成本比为3∶1。 Step4将全部样本的生存概率Sj(T)逐一作为阈值K,重复Step1~Step3,得到不同阈值下的错误成本r。选取判定错误成本r最小的那个阈值K*作为最终的预警阈值。 本研究以中小企业为实证对象,选取2008~2017年中小企业板上市的701家中小企业作为实证样本,以2008~2017年的企业数据作为训练集、以2018年的企业数据作为测试集。本研究中协变量数据Z(t)采用2008~2017年10年的面板数据,数据来自于Wind数据库。 本研究以企业被证监会发出退市预警“*ST”作为发生财务危机的标志。被*ST的企业是已连续亏损两年或存在重大的报表造假,具有退市风险。这说明该企业的财务状况严重恶化,投资该企业会造成亏损。 对于生存时间的界定,本文的观测起点是企业的上市日期。对于财务困境的企业,观测终点是被*ST的时间。对于正常健康的企业,观测终点是2017年12月31日。总的来说,生存时间即为企业上市日至被*ST或观测期结束(2017/12/31)的时间。 借鉴中诚信、联合资信等权威评级机构及经典文献中的高频指标,选取了反映偿债能力、盈利能力、经营能力、企业规模21个财务指标。如表1中Z1~Z21。 根据大量的研究表明,公司治理水平与企业业绩成正相关,与企业违约概率呈显著的负相关系[24]。所以本文在经典的财务预警指标基础上,参考了MSCI[25]、南开公司治理课题组[26]的公司治理评价方法,增加了反映关联交易、薪酬激励、股权结构、董监高信息、研发投入等13个公司治理评价指标。如表1中Z22~Z34。 相较于大型上市企业,中小企业规模小、抗风险的能力差,所以比较容易受到外部宏观环境的影响,所以在海选指标中引入了8个反映宏观环境的指标,如表1中Z34~Z42。 加之,反映企业行业地区信息的两个指标Z43、Z44。总共形成了涵盖财务因素、公司治理、宏观环境等维度共44个海选预警指标体系,如表1所示。 表1 财务预警的海选指标 利用上文1.1的共线性检验方法,对海选的44个指标计算方差膨胀因子VIF,删除方差膨胀因子VIF>10的7个指标“速动比率”、“现金比率”、“管理层年度薪酬总额”、“社会消费品零售总额”、“人均地区生产总值”、“全社会固定资产投资”、“M2”,避免指标之间的共线性。经过共线性检验的初筛,剩余37个评价指标进入下一步的Cox回归模型。 将“是否发生被标记*ST(是为1、否为0)”、“生存时间T”作为因变量,“生存时间T”的界定如前3.1所述。将共线性检验后筛选后的37个指标2008~2017年的面板数据作为协变量Zi(t)代入时间相依Cox回归模型式(4)中。其中,指标“董事长和总经理是否兼任”、“薪酬弹性系数(正为1、负为0)”、“所属行业”、“所在省份”作为哑变量,其余指标作为定量变量。利用式(5)、(6)分别对基准危险强度h0(t)和回归系数βi进行拟合。 本文采用“向后法”进行Cox回归,先将共线性检验后剩余的37个变量一起放入Cox回归中进行拟合,再逐一删除不显著的指标,每步删去对回归方程F值影响最小的指标。最终剩余指标为表2中的10个指标,均对因变量“是否发生财务危机”有显著影响。采用“逐步向后”的方式,最终保留的指标及拟合结果如表2所示。上述过程通过R软件编程,程序见附件。 表2 时间相依Cox回归参数拟合结果 表2中的10个指标的显著性Sig.值小于0.1,说明这10个指标对于中小企业的财务风险具有显著影响。 判断10个指标的风险属性:保护因素是回归系数为负的指标,其数值越大企业财务风险越低;危险因素是回归系数为负的指标,其数值越大企业财务风险越高的指标。因此,投资者应该更为关注保护因素数值的下降,以及危险因素数值的上升,说明企业的财务风险正在增加。 表2最后一列为10个指标的风险属性,具体分析如下: (1)盈利能力维度包含三个指标:“净资产收益率ROE”、“销售毛利率”的回归系数显著为负,说明企业的利润率越高财务状况越好,均为保护因素;“销售期间费用率”的回归系数显著为正,是危险因素,企业的成本费用率越高财务风险越高。因此,盈利能力是对中小企业财务风险影响最为显著的维度。 (2)公司治理维度包含两个指标:“研发支出总额占营业收入比例”的回归系数显著为负,说明提高研发投入提升研发能力有助于企业财务优化,是保护因素;“赫芬德尔指数”的回归系数显著为正,说明中小企业中其他股东对于第一大股东的股权制衡度越大、股权过于分散会使中小企业面临更大的财务风险,是危险因素。因此,公司治理水平的提高对中小企业财务状况优化有促进作用。 (3)“所属行业”分类变量下:“所属行业_9(属于电力、热力、燃气及水生产和供应业)”的回归系数显著为负,说明电力、热力、燃气及水生产和供应业的企业相对于其他行业财务风险更低,是保护因素。“所属行业_10(住宿和餐饮业)”的回归系数显著且为正,说明住宿和餐饮业相对于其他行业财务风险更高,是危险因素。因此,中小企业的财务风险具有行业差异性。 (4)现金流、资产周转能力等其他维度包含:指标“经营活动产生的现金流量净额/负债合计”、“所有者权益合计”、“总资产周转率”的回归系数均显著为负,说明经营性现金流越大、资产规模越大、资产周转能力越强,中小企业的财务风险越低、信用状况越好,均是保护因素。因此,现金流、资产规模、资产周转能力对于中小企业的财务状况都有显著的正向影响。 根据式(5)对基准危险强度h0(t)进行测算,进而计算基准危险强度h0(t)的累计值,即累积基准危险强度H0(t),结果如图1所示。 图1 累积基准危险强度H0(t) 图2 在协变量均值处的生存函数 由图2可见,生存函数是一个分段函数,图中横轴是生存时间(年)、纵轴是生存概率S(T)。中小企业一般在3年后生存概率开始缓慢下降,达到9年左右开始急剧下降。 2.4.1 财务预警阈值的确定 利用上文1.4的反推最优阈值的思路,得到预警的阈值K=0.996,当企业的生存概率S(T)低于0.996时发生财务预警。在预警阈值K=0.996下样本内判别的加权正确率最高达到89%。 2.4.2 样本外检验 上文利用701家中小企业2008~2017的数据作为训练集建模,本部分是利用训练出的模型对2018年的企业财务风险(是否*ST)进行判别,并与真实是否发生财务风险进行对比,结果如表3所示。 从表3中,实际发生财务困境的企业被正确识别的概率78%,实际正常企业被正确识别的概率为66%,模型的加权正确率达到75%。说明本文建立的基于时间相依Cox回归的财务预警模型精度较高,尤其是对财务危机企业的正确识别率超过70%,具有较好的财务风险识别能力。 表3 模型的判别结果 将本研究的基于时间相依Cox回归的预警模型与Cox回归、逻辑回归进行对比分析。对比模型的构建仅是将本研究的“时间相依Cox模型”分别替换成“一般的Cox模型”、“逻辑回归”,而其他步骤包括样本的选取范围、指标选取初筛、阈值的确定均不变。 本文采用三折交叉检验的方式,进行三组对比分析。将全部701个样本分成三份,取任意两份样本作为训练集、另一份样本作为检验集。在检验集上得到对财务风险判别的加权正确率,如表4所示。 表4 对比结果 由表4可以看到,本模型相比对比模型“一般的Cox模型”、“逻辑回归”的加权正确率更高。将本模型的三组正确率(表4第1行)分别与两个对比模型的三组正确率(表4第2、3行)进行t检验,得到:在5%的显著性水平下,本模型的正确率高于对比模型“Cox回归”(p值=0.037);在10%的显著性水平下,本模型的正确率高于对比模型“逻辑回归”(p值=0.098)。因此,本模型“基于时间相依Cox回归的预警模型”的判别正确率显著高于对比模型“一般的Cox模型”、“逻辑回归”,说明本模型对于财务风险的判别精度更高、高危企业的识别能力更强。 (1)通过预警精度检验和对比分析,本文建立的基于时间相依Cox回归的财务预警模型精度较高,尤其对财务危机企业的正确识别率达到75%。相较于传统的Cox回归、逻辑回归模型,财务危机企业的正确识别率更高、且财务风险识别的错误成本更低。说明本模型对于财务风险高危的企业识别能力更强。 (2)经过实证,盈利能力是对中小企业财务风险影响最为显著的因素。主要包含三个影响显著的指标:“净资产收益率ROE”、“销售毛利率”是保护性因素,企业的利润率越高财务状况越好;“销售期间费用率”是危险因素,企业的成本费用率越高财务风险越高。 (3)经过实证,公司治理水平的提高对中小企业财务状况优化有促进作用。主要包含两个显著的指标:“研发支出总额占营业收入比例”是保护因素,提高研发投入提升研发能力有助于企业财务优化;“赫芬德尔指数”是危险因素,赫芬德尔指数越高、股权分散度越大,说明股权过于分散会使中小企业面临更大的财务风险。 (4)经过实证,中小企业的财务风险具有行业差异性。“电力、热力、燃气及水生产和供应业”的回归系数显著且为负,说明电力、热力、燃气及水生产和供应业的企业相对于其他行业财务风险更低。“住宿和餐饮业”的回归系数显著且为正,说明住宿和餐饮业相对于其他行业财务风险更高。 (1)通过时间相依Cox回归模型,构建随时间而变化的预警指标数据与财务危机之间的函数关系。利用偏似然估计、Breslow估计量分别拟合回归系数和基准危险强度,构建财务预警模型,预测企业在未来一段时间内每个时间点上的财务危机概率。相比于基于传统Cox模型的预警研究仅用一期的截面数据建模,本研究考虑了预警指标的动态变化对财务风险的影响,涵盖了更多的历史信息,达到提高预警精度的目的。 (2)考虑第一类错误“危机企业判为正常”与第二类错误“正常企业判为危机”给投资者造成的损失差异,衡量预警的“错误成本”,以错误成本最低为目标,反推出财务正常和财务危机之间的预警阈值,实现了对财务危机发生与否的提前预警功能。1.3 生存函数

1.4 财务危机预警
2 实证分析
2.1 样本的选取
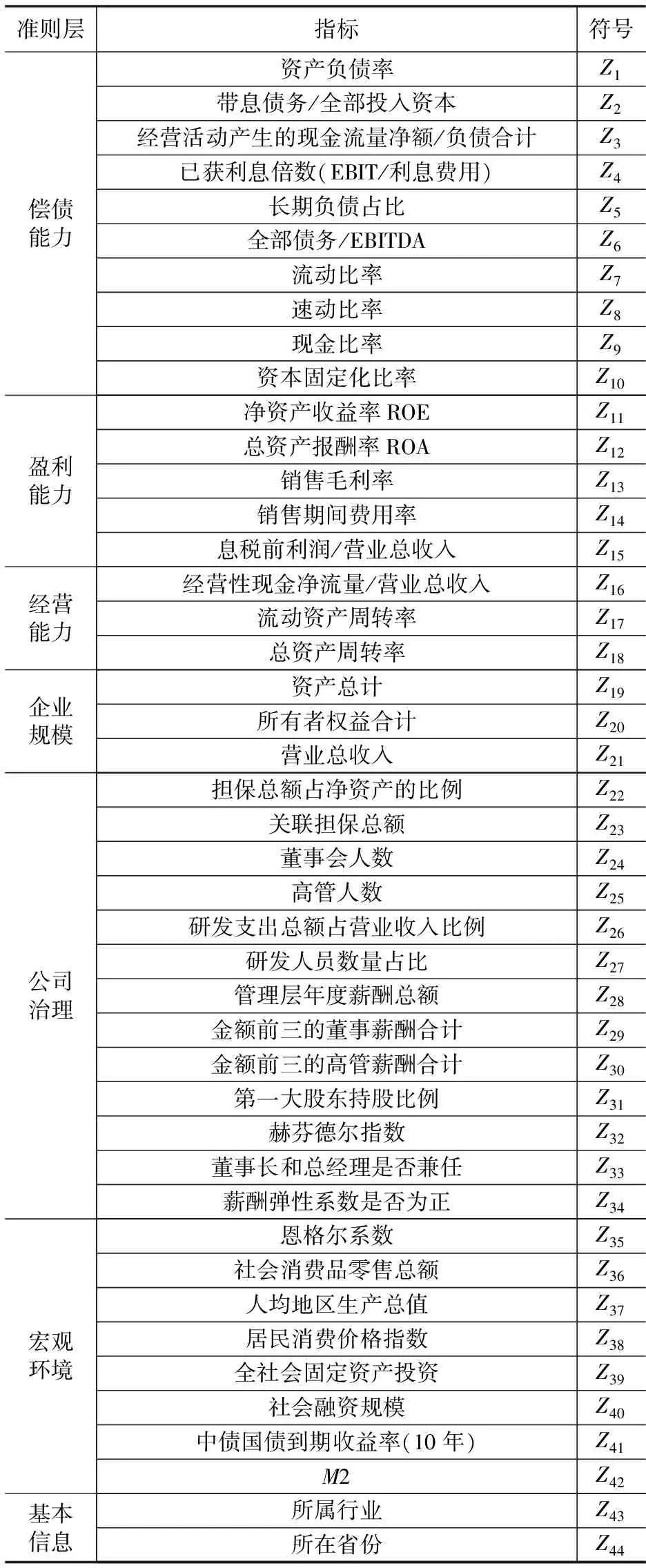
2.2 预警指标选取和初筛
2.3 预警模型构建
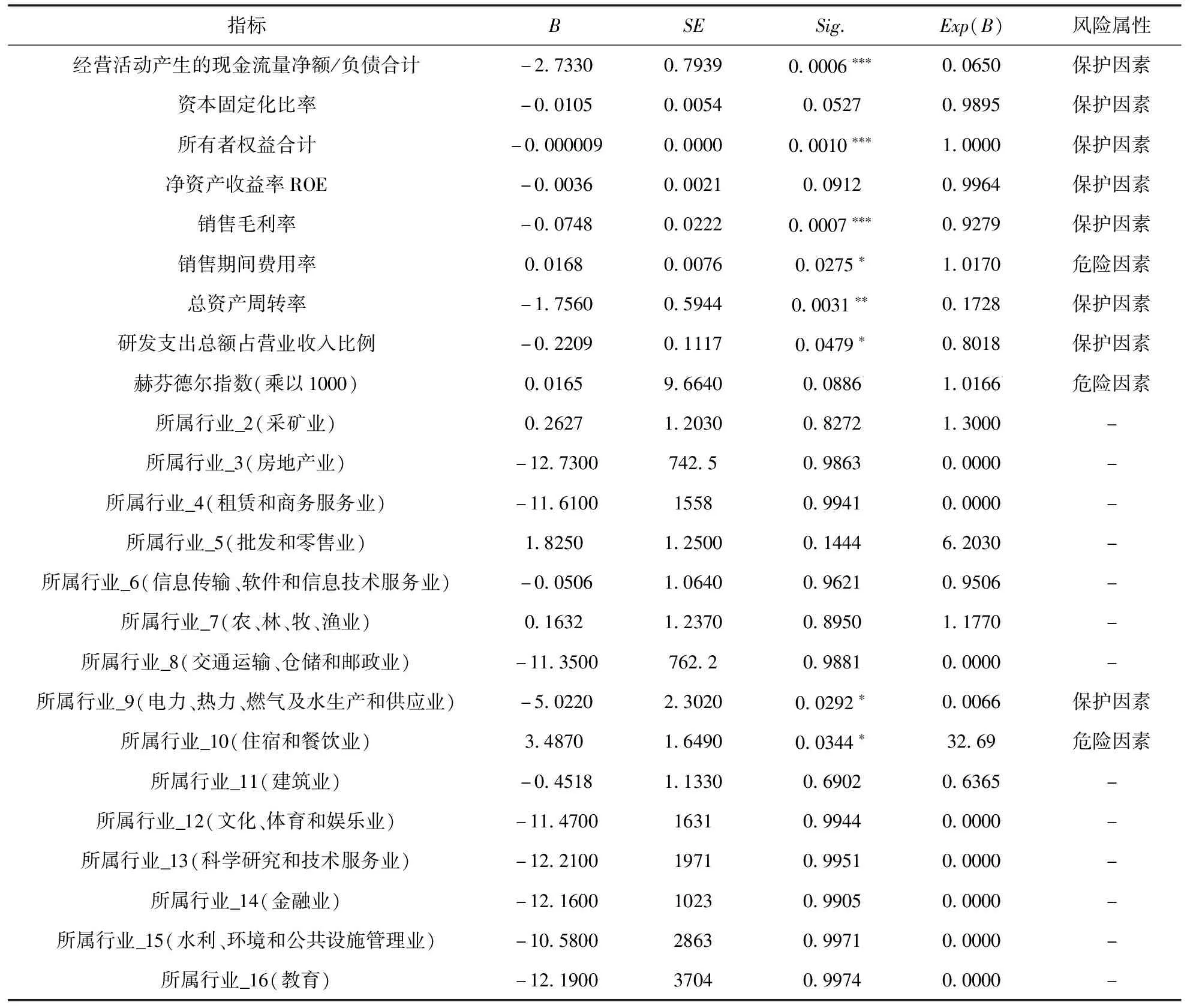
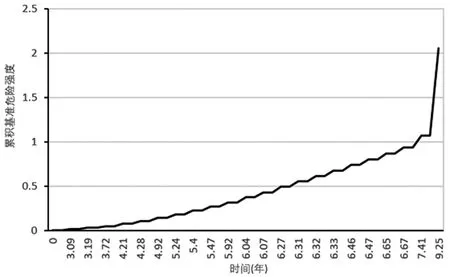
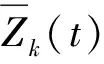

2.4 财务预警效果检验

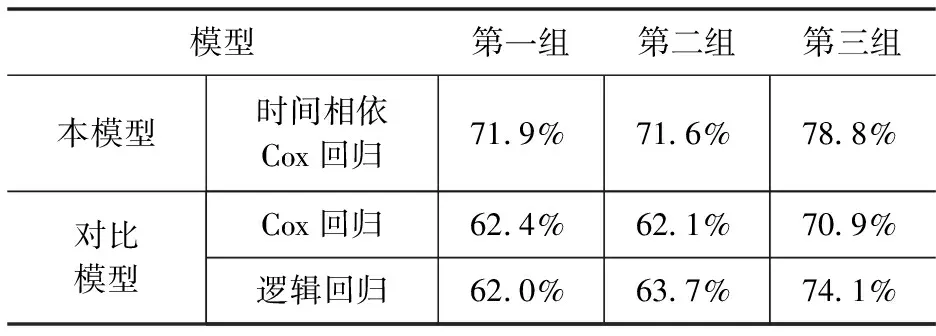
2.5 对比分析
3 结论
3.1 主要结论
3.2 创新特色

