基于改进PSO-BP神经网络的贮存可靠性预测
宫 华, 李作华, 刘洪涛, 郝永平
(1.沈阳理工大学 理学院,辽宁 沈阳 110159; 2.辽宁华兴机电有限公司,辽宁 锦州 121017; 3.沈阳理工大学 装备工程学院,辽宁 沈阳 110159)
0 引言
军用产品的可靠性水平是军事储备中衡量产品质量的一项关键技术指标,是衡量国家军事后勤保障技术水平的重要依据。武器系统等产品大部分处于贮存、维护和检测等非工作状态,具有长期贮存、一次性使用的典型特征。由于贮存环境温度、湿度、年限等因素影响,产品的质量与存储寿命必然随之发生变化。若达到实际贮存寿命而超期服役,则增加了武器产品贮存和使用的不安全性。而未达到实际贮存寿命而提前退役的,将会造成大量的经济损失。因此,针对武器产品贮存可靠性进行科学准确预测研究,预知产品质量与储存变化规律,能够为军方提供订购生产、储备布局和维护检测的决策依据。然而可靠性工程中所收集的各种贮存可靠性数据,对数据自身规律的解析不足。如何有效地利用已知历史数据,挖掘数据本身所隐藏的信息进行可靠性预测,将数据转化为决策以提高军事政策制定与评估的科学化和智能化程度,是实现军事现代化的必然要求。
贮存可靠性预测是指预测产品在一定的贮存条件下和一定的贮存时间内保持产品指定功能能力的概率值。针对数学机理模型和加速寿命试验的贮存可靠性预测已有很多学者进行了相关研究。Mense等人[1]详细综述了贮存可靠性的评估模型与方法。Zhang等人[2]针对初始故障参数测量提出E-Bayes估计方法对贮存可靠性进行预测。Zheng等人[3]基于测试数据的通道对系统贮存可靠性进行评估。Su等人[4]、Zhang等人[5]基于指数分布前提下研究考虑定期检测的产品贮存可靠性预测问题。Si等人[6]针对剩余贮存寿命建立二阶连续时间齐次马尔可夫预测模型。Wang等人[7]基于状态监测影响的随机滤波预测剩余寿命。赵志草等人[8]在应力下失效分布函数基础上对加速寿命试验进行可靠性评估。尽管上述文献从机理模型出发对可靠性预测方面进行了相关研究,但传统的贝叶斯等机理模型很大程度上依赖于先验分布及对机理的认知。而军品的结构、功能、失效模式、贮存的环境条件等虽然相似,但对贮存可靠性变化影响差异较大,指标与相关变量之间具有非线性关系。在机理不明确条件下,传统的数学机理模型所建立的贮存可靠性预测方法并不适用。
在可靠性预测方法上已有在人工神经网络及智能优化预测方法的相关研究。邹心遥等人[9]将支持向量机和Bayes方法结合评估小子样可靠性。章恩泽等[10]提出区间多目标粒子群算法解决可靠性优化问题。Liu等人[11]针对导弹部件在变温条件下的贮存可靠性评估进行研究。陈海建等人[12]提出基于BP和RBF两种神经网络对弹药贮存可靠性进行预测方法研究。已有研究表明人工神经网络对可靠性的预测研究具有较好的预测效果。尤其是神经网络描述输入输出可实现任意复杂的非线性函数映射,容错能力强,易于实现。然而许多军用产品试验样品不多,需要长期观测且样本量偏少。尽管文献中已有基于人工神经网络对可靠性进行的预测研究,但在基于小子样的贮存可靠性预测的泛化能力受到一定影响,进而影响预测结果。当样本数据量不充分时,如何有效利用贮存历史数据挖掘出产品可靠性变化,改进神经网络预测方法及分析质量规律是亟待解决的问题。
综上分析,本文从数据、模型、预测方法上对贮存可靠性预测进行研究,主要贡献如下:(1)针对贮存年限、可靠度的历史数据,基于年限与可靠度的时间序列建立贮存可靠度预测模型。直接从数据中揭示变化规律作为输入与可靠度作为输出之间的关系,消除由于不明确机理带来的模型误差。(2)为提高预测的泛化能力,采用横向数据进行样本数据集扩充,提高样本的数量与质量,解决样本量偏少对预测的泛化能力和精度影响。(3)将粒子群(PSO)算法的全局搜索和BP神经网络的局部搜索相结合,通过迭代预测未来武器产品贮存的变化趋势。引入进化策略改进PSO算法,根据进化状态优化BP神经网络的拓扑结构,进行神经网络权值和阈值优化,提高神经网络收敛速度和训练质量,提高贮存可靠性预测精度。
1 BP神经网络及PSO算法
1.1 数据处理
贮存可靠度R(t)是保持规定功能的概率,是衡量储存可靠性的指标,表示为:R(t)=P(ξ>t),其中ξ为产品失效前贮存的时间,t为规定的贮存时间。根据产品的可靠性结构、寿命模型及其他试验数据,利用概率方法对产品或部件可靠度的特征量R(t)进行统计推断。贮存寿命的可靠性预测是指通过贮存可靠度的已知数据对未来时刻的可靠度进行估计。设某型号部件可靠度在年份时间序列t1,t2,…,tn上的贮存可靠度为R(t1),R(t2),…,R(tn),对于未来年份tn+1的可靠度R(tn+1)进行预测,预测函数表示为:R(tn+1)=f(R(t1),R(t2),…,R(tn),tn+1)。年份与可靠度形成时间序列作为数据的输入与输出,进行神经网络结构的训练与测试。
1.2 BP神经网络
BP神经网络是一种包括正向传播和反向传播学习的有监督、多层前馈神经网络。前向传播过程是指训练样本由输入层通过隐含层训练进行网络输出。当输出值与期望输出值误差较大时,转入误差反向传播过程。通过误差值调整神经网络的权值和阈值,使得网络输出逼近期望值。设输入层为n个神经元,表示在时间序列t1,t2,…,tn上贮存可靠度的历史数据,输出层m为1个神经元,代表贮存可靠度在tn+1时刻的预测值。
BP神经网络训练过程描述如下:
Step1输入数据和输出数据的归一化处理:
(1)
其中Rmax和Rmin表示数据集中贮存可靠度的最大值和最小值,为贮存可靠度的历史数据实际值。
Step2计算隐含层所有节点的输出,i=1,…,n;j=1,…,h,
(2)
(3)
其中节点j的激活变量为netj,输入层节点i到隐含层节点j的连接权值为wij,节点j的输出阈值与输出量分别为bj和yj,选用S型函数f(·)为隐含层激活函数。
Step3计算神经网络的输出结果:
(4)
其中隐含层节点j到输出层连接权值为woj,输出层阈值为bo,第k组训练样本的可靠度预测值为Rk,输出层激活函数为g(·)。
Step4运用反向传播,修正神经网络的权值和阈值,最小化训练误差MSE:
(5)
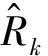
1.3 基本粒子群优化算法
粒子群算法[14](PSO)是一种来源于对鸟群觅食行为模拟的智能优化算法。随机初始化一群粒子,通过迭代找到个体极值与全局极值更新粒子的位置,寻求最优解。假设存在N个粒子的种群在D维解空间中进行搜索,Xi=(xi1,…,xiD)代表第i个粒子的位置矢量,Vi=(vi1,…,viD)为第i个粒子的飞行速度,i=1,…,N。根据公式(6)(7)更新自身的速度和位置,产生新种群。由适应度函数计算每个粒子的适应度值,进而确定个体与全局最优值。
(6)
(7)
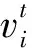
(8)
其中wmax和wmin分别为惯性权重的最大值和最小值,通常取0.9和0.4,Tmax为最大迭代次数。
1.4 进化策略(ES)改进PSO算法
本文根据粒子群的进化状态采用Schwefel[15]提出的进化策略,使用适应高斯突变优化参数。进化策略产生小高斯突变的概率较大,能有效避免局部最优,提高PSO优化算法收敛速度寻求全局最优解。进化策略(ES)思想为:将粒子状态划分为正常和早熟两种状态,设置阈值limit,记录全局最优值连续没有更新的次数。若次数>limit时Pg没有更新,则认为种群处于早熟状态,否则为正常状态。早熟状态时通过改变步长的速度,粒子速度更新公式为(9)(10),重新更新Pib和Pg。
(9)
(10)
2 优化BP神经网络
训练样本的数量、质量、初始权值和网络结构复杂性等影响自身的拟合程度和预测精度,是影响网络泛化能力的决定因素。由于BP神经网络初始权值的随机性可能会导致不同预测精度,训练容易陷入局部最优,存在多个局部极值,使得网络结构难以确定。而武器产品长期储存,样本数据的数量不够充分,直接采用BP神经网络进行预测,其泛化能力及预测精度均受到影响。本文采用以下三种方法进行神经网络的改进与优化。(1)扩大样本数量,避免过拟合。(2)根据输入层、输出层的神经单元数和样本数量,确定隐含层节点数,避免参数的盲目选择。(3)基于改进的进化策略PSO算法,优化初始权值阈值,克服BP神经网络的缺点,提高预测精度。
2.1 数据集扩充
对于样本数据量不充分的数据集,不同的输入数据集选择方法将导致不同预测结果。本文采用横向数据集作为输入数据集。
将原始数据按照时间序列从1到n进行编号,确定输入数据集维度d=5。假设i为样本选择的开始点,则训练样本的第一组输入为R(ti+1),…,R(ti+d),输出为R(ti+d+1)。训练样本的第二组输入为R(ti+d+1),…,R(ti+2d),输出为R(ti+2d+1)。以此类推,训练样本的第k组输入为R(ti+(k-1)d+1),…,R(ti+kd),输出为R(ti+kd+1)。测试样本根据下列规则进行选择:测试样本的第一组输入为R(ti+2),…,R(ti+d+1),输出为R(ti+d+2)。测试样本的第二组输入为R(ti+d+2),…,R(ti+2d+1),输出为R(ti+2d+2)。以此类推,测试样本的第k组输入为R(ti+(k-1)d+2),…,R(ti+kd+1),输出为R(ti+kd+2)。训练集与测试集的选择过程如图1所示。
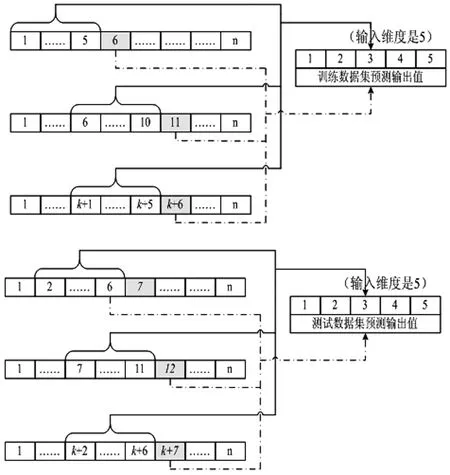
图1 构造数据集的过程
2.2 隐含层确定
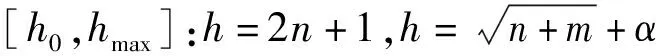
2.3 ES-PSO-BP算法
粒子群算法具有较强的全局搜索最优解能力,BP神经网络具有较强的局部搜索最优能力,其初始权值和阈值在[0,1]之间产生。因此,将权值阈值定义为PSO中的粒子位置,基于进化策略,将种群分为正常和早熟状态。通过最优粒子位置的寻优过程优化网络结构,提高算法的收敛速度和贮存可靠度的预测精度。
ES-PSO-BP模型的整体流程如图2所示,算法具体描述如下。
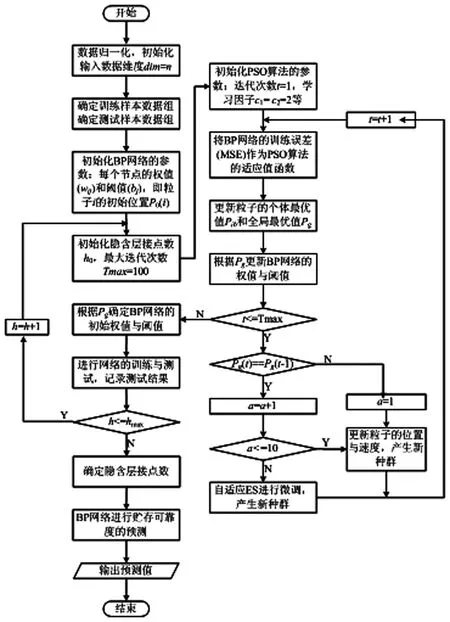
图2 ES-PSO-BP模型的流程图
Step1数据集归一化,构建网络结构。
Step2根据年限形成的可靠度时间序列,确定训练样本集与测试样本集。
Step3初始化粒子群参数。种群规模、最大迭代次数、权值、学习因子、状态划分阈值limit等参数。
Step4在[0,1]范围随机初始化N个粒子的位置与速度,粒子维度D=(n+m)*h+h+m。
Step5计算粒子的初始个体与全局最优适应度值。设定粒子的适应度函数为BP神经网络的训练误差函数,根据适应度值确定粒子个体最优和种群全局最优值。
Step6根据种群进化状态,更新粒子速度与位置。比较全局最优值连续没有更新的次数与阈值limit。若次数>limit时,种群处于早熟状态,则根据进化策略式(9)与(10)更新粒子速度和位置产生新种群。否则处于正常状态,根据式(6)与(7)更新粒子的速度和位置产生新种群。粒子的速度和位置不能超过[-vmax,vmax]和[-xmax,xmax]的范围。
Step7计算粒子的适应度值与全局最优适应度值,若当前粒子适应度值优于历史最优值,则更新当前个体最优值为Pib,同时更新全局最优位置Pg。若达到最大迭代次数,则转向Step 8,否则回到Step 6。
Step8将Pg映射到BP神经网络的权值与阈值。对BP神经网络进行网络训练,若隐含层节点数满足最大值hmax,执行Step 9,否则执行Step 4。
Step9根据网络训练性能指标确定隐含层节点数,输入测试样本集进行贮存可靠度预测。
3 实验仿真
为验证本文所提出的算法对贮存可靠性预测的有效性,以某弹药部件的贮存历史可靠度数据为例进行实验。R(t1),R(t2),…,R(tn)形成的时间序列为BP神经网络的输入数据,R(tn+1)为网络的输出值即预测值。根据历史数据,选取某型号弹药部件4年(48个月)的平均贮存可靠度数据,样本数据如表1所示。将原始数据按照时间序列从1到48进行编号,确定输入数据集维度d=5。

表1 样本数据集
3.1 参数选择及性能指标
为说明ES-PSO-BP算法预测的准确性,将BP、PSO-BP和ES-PSO-BP神经网络三种算法进行对比分析。参数设置如下:
BP神经网络结构:输入n=5,输出m=1,选取“tansig”和“purelin”为传递函数。选取动量BP法“traingdm”为训练函数,最大训练次数设为10000,期望误差设置为0.001,学习率为0.01。由经验公式计算的隐含层节点数的取值范围:h0=4,hmax=13。
ES-PSO算法:粒子数N=30,解的维度(及粒子位置的维度)D=(n+m)*h+h+m=78。学习因子c1=c2=2.0,阈值limit=10,最大迭代次数Tmax=100。
选取4个性能指标评估预测精度:
平均误差:
(11)
平均绝对误差:
(12)
均方差:
(13)
平均绝对百分误差:
(14)
需要指出:MAE表示平均绝对误差值,避免误差有正有负的中和问题。MSE表示预测均方误差平均值,用来评价预测结果的变化程度,其中MSE值越小表明预测效果越好。MAPE用来评价预测方法的准确性。
3.2 隐含层节点数的确定
对BP神经网络、PSO-BP和ESPSO-BP在节点数[4,13]范围内依次进行50次试验,训练结果的平均数据如表2所示。本文通过网络MAPE值确定隐含层节点数,三种网络都在隐含层节点数为8时取到最小的MAPE值,三种网络训练效果都较好。因此,选取隐含层节点数8进行网络训练。
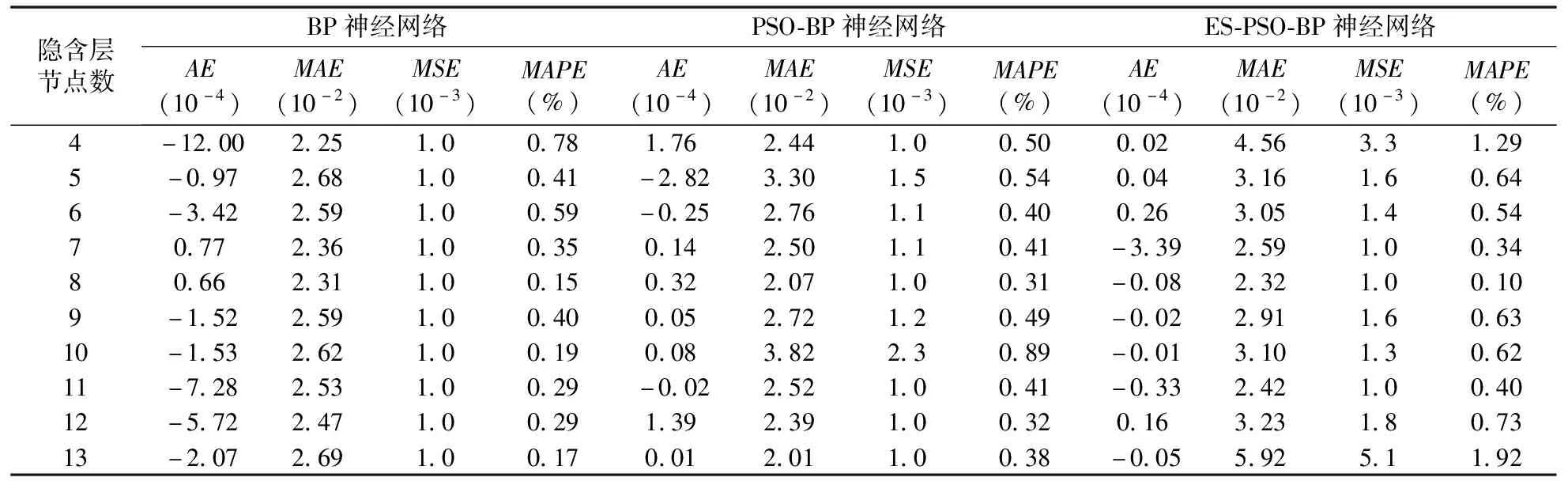
表2 三种网络训练的性能指标
3.3 训练过程分析
如图3、图4所示,网络均可以达到期望误差精度MSE=0.001,但ES-PSO-BP神经网络收敛速度最快,BP网络在迭代4877次达到期望误差,PSO-BP网络迭代530次,而ES-PSO-BP网络迭代274次可实现收敛。从MSE变化曲线可知,PSO-BP和ES-PSO-BP网络的训练过程明显比BP网络更平稳。图5~7表明,BP神经网络的训练拟合精度达到98.42%,PSO-BP网络达到98.43%,而ES-PSO-BP网络达到98.45%。显然ES-PSO-BP网络训练拟合精度逼近能力最强,与BP和PSO-BP网络相比,相应的贮存可靠度的预测精度最高。图8表明ES-PSO算法找到6次最优解,适应度值为0.001,均方差MSE更小。
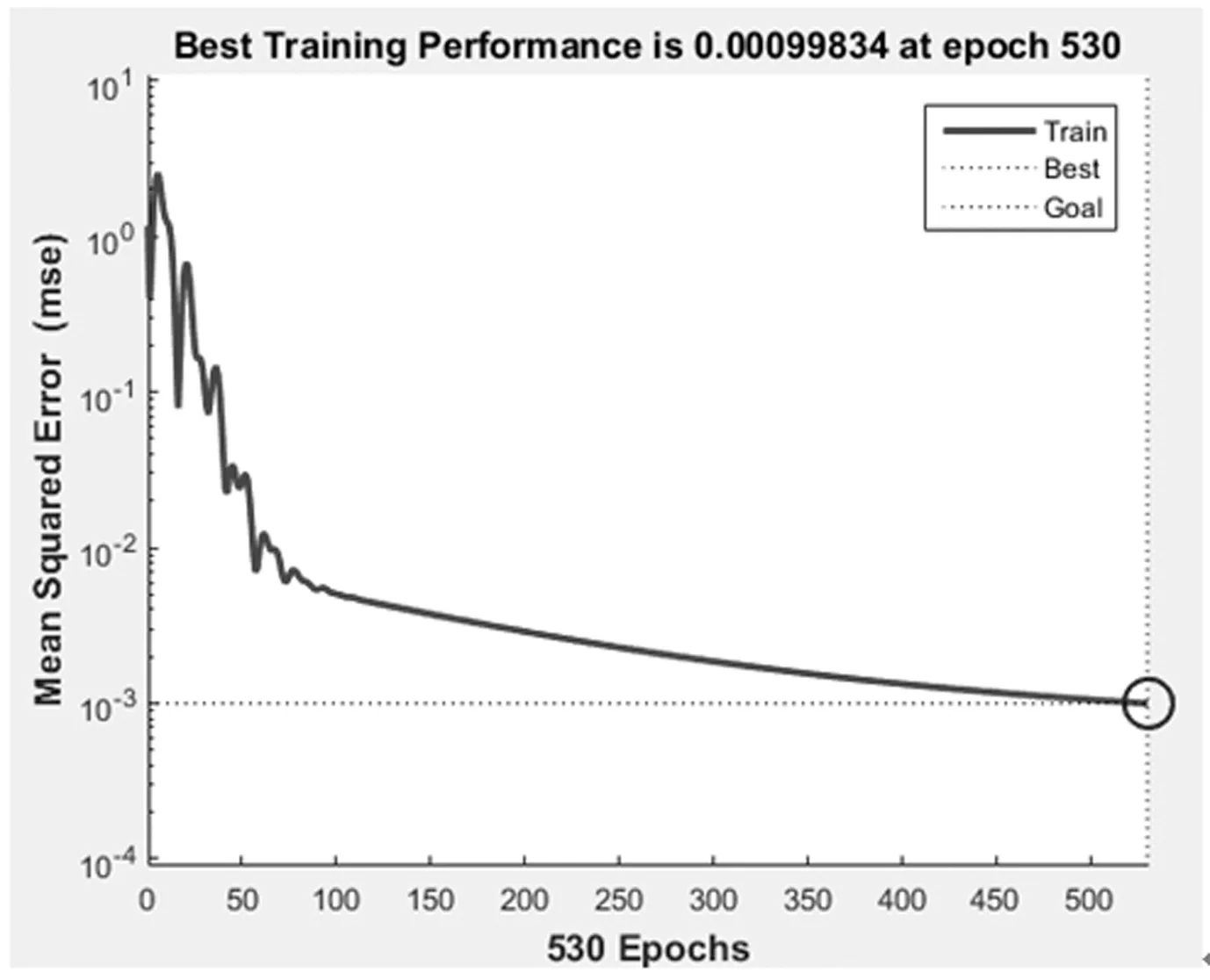
图3 PSO-BP网络训练曲线
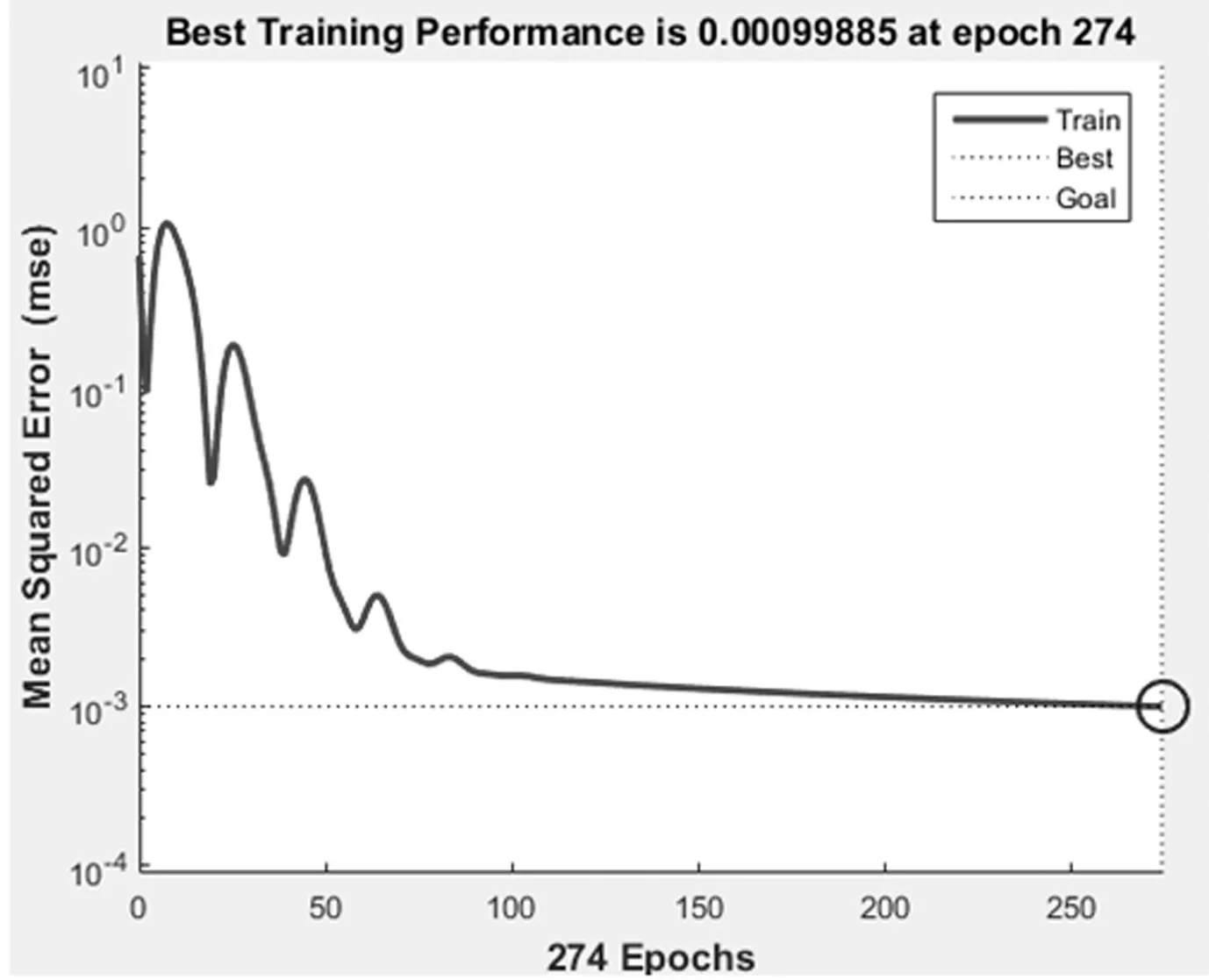
图4 ES-PSO-BP网络训练曲线
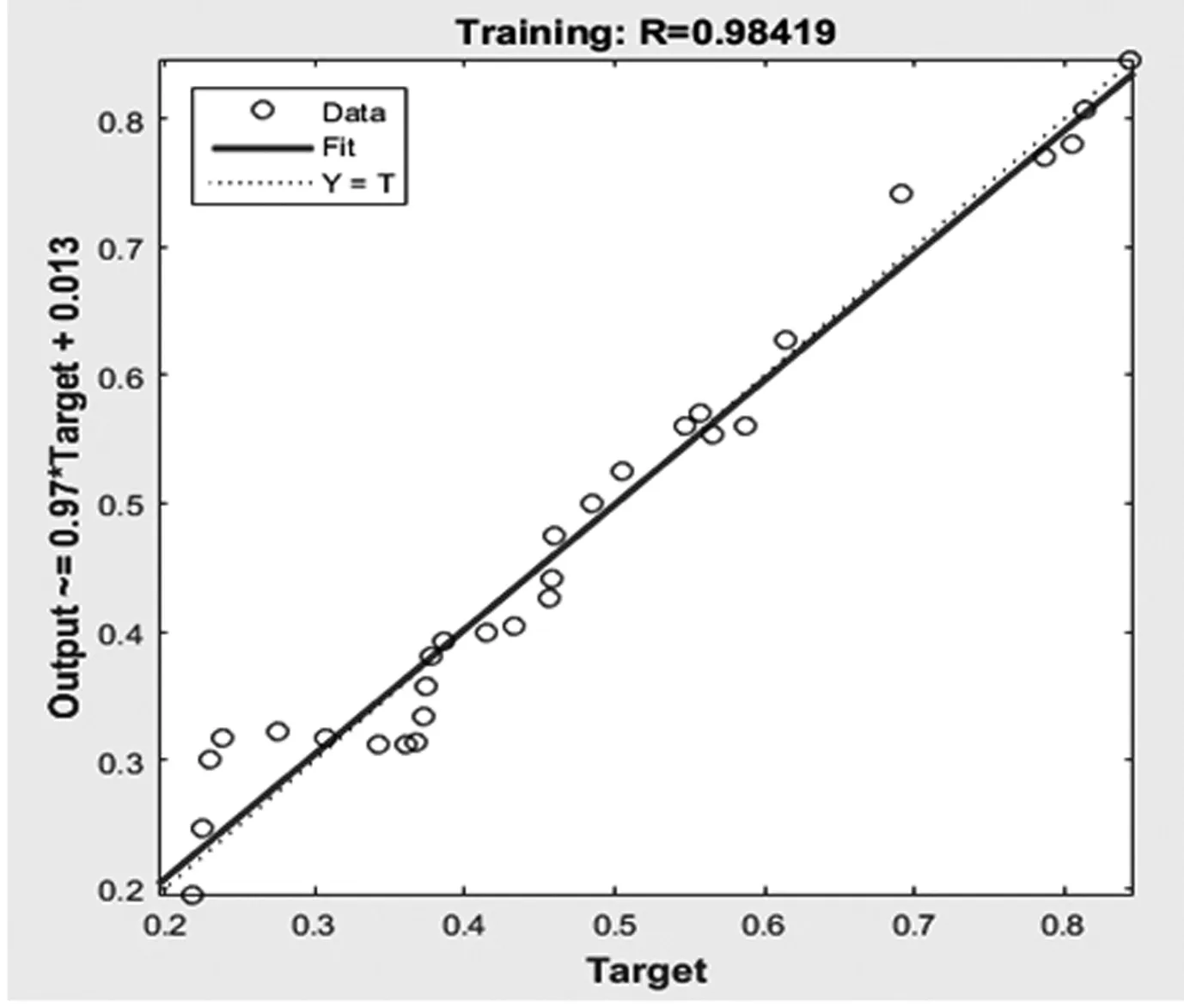
图5 BP网络训练拟合精度
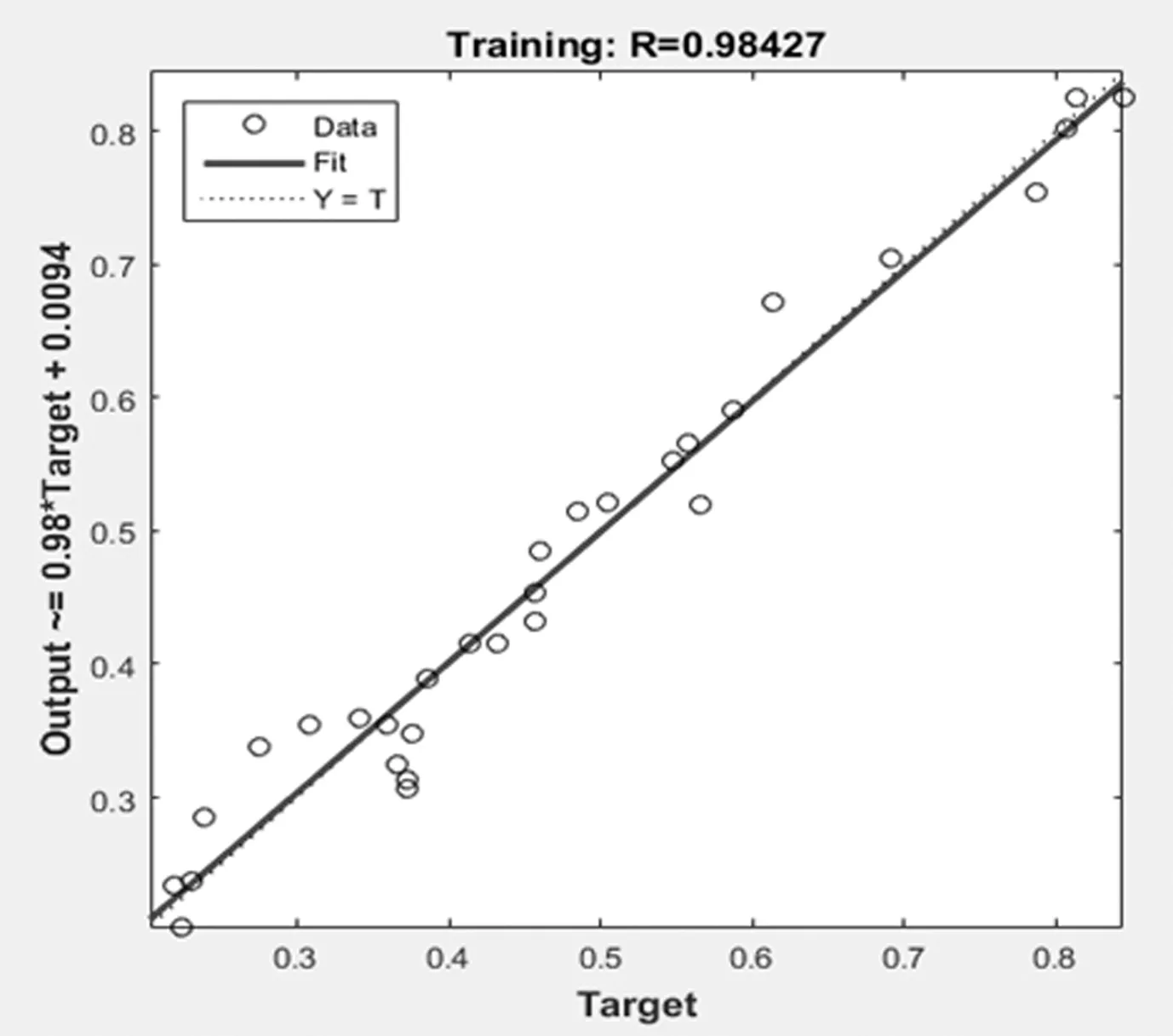
图6 PSO-BP网络训练拟合精度
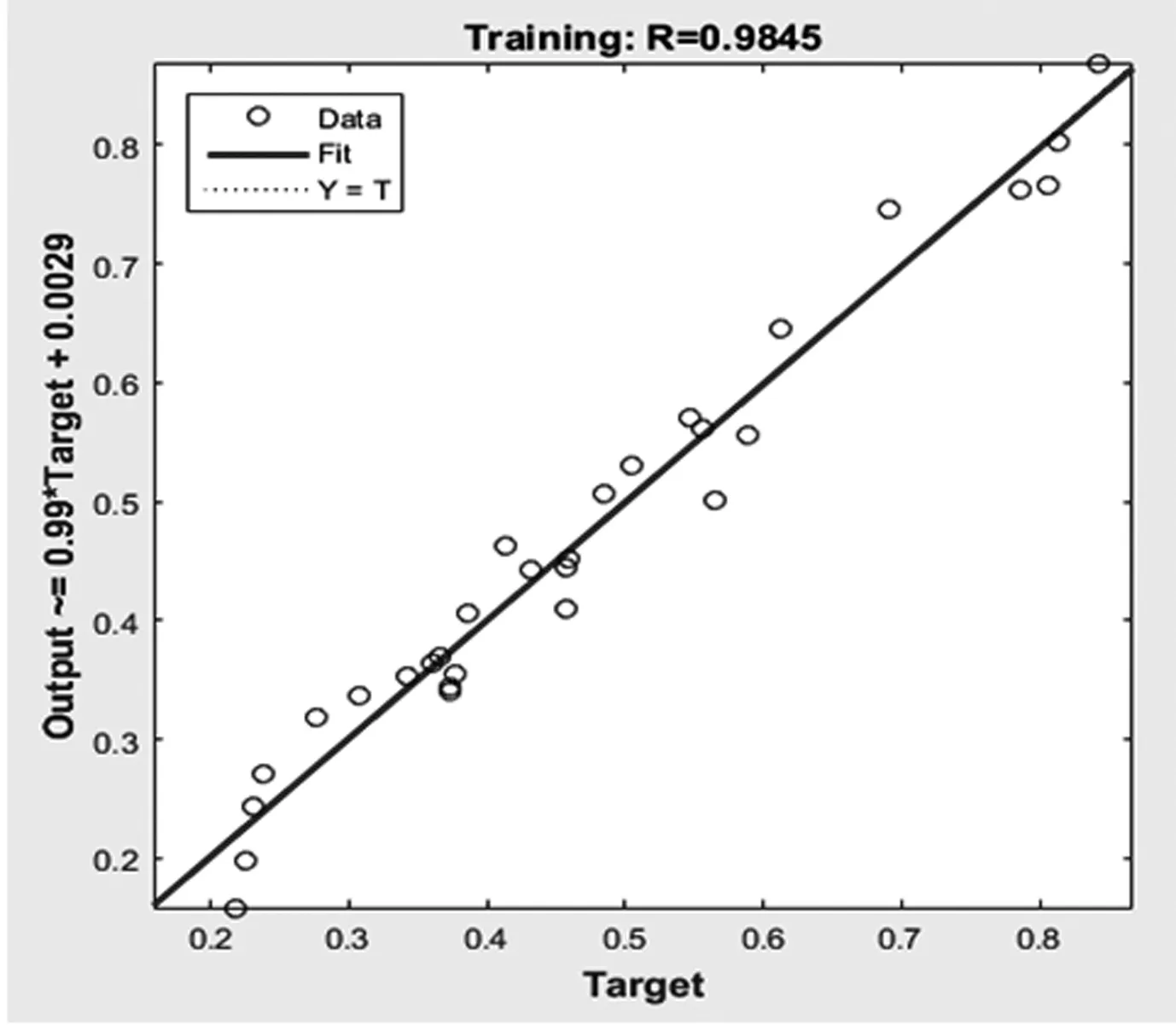
图7 ES-PSO-BP网络训练拟合精度
3.5 结果比较
图8表明PSO-BP粒子寻优过程迭代6次后收敛,出现早熟现象。当全局最优值连续10次不变时,提出的进化策略优化PSO-BP算法,从ES-PSO收敛曲线中可以看出粒子多次跳出最优值进行搜索,避免了过度拟合与陷入局部最优。表3对弹药贮存可靠度进行的三种预测模型结果进行对比,ES-PSO-BP网络模型的鲁棒性和预测性能更好,获得更小的AE、MAE、MSE和MAPE值。与BP神经网络与PSO-BP网络相比,图9~10表明ES-PSO-BP网络的预测值更逼近期望预测值,绝对误差和与误差波动范围更小。
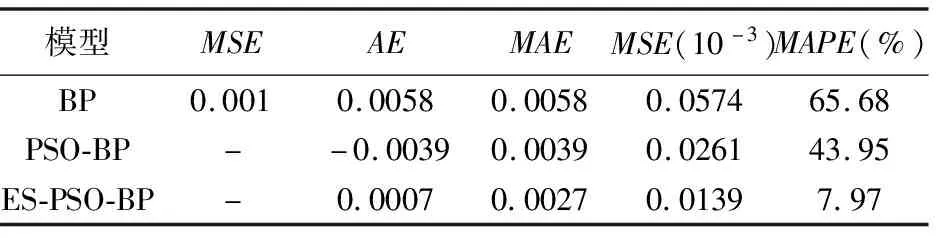
表3 三种网络的预测结果的比较
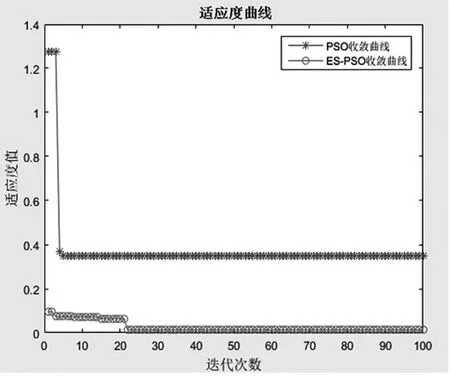
图8 PSO与ES-PSO的收敛曲线
4 结论
针对军用产品非线性结构及机理不确定情况,根据贮存年限和可靠度历史数据构造时间序列,采用横向数据集方法扩充数据,提高样本的数量与质量,从而建立贮存可靠度预测数学模型。通过进化策略改进粒子群的方法优化BP神经网络中的网络权值和阈值,通过确定隐含层节点数训练网络模型,优化神经网络的拓扑结构。实验结果表明,本文提出的ES-PSO-BP算法与BP神经网络、PSO-BP算法相比,能够显著提升神经网络收敛速度和训练质量,提高贮存可靠性预测精度,进而提升军事决策与评估的科学能力。

