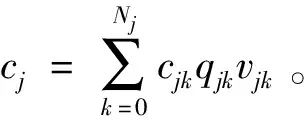多态防护系统可靠性及重要度分析
兑红炎, 白光晗
(1.郑州大学 管理工程学院,河南 郑州 450001; 2.国防科技大学 智能科学学院,机电工程研究所兼国防科技重点实验室,湖南 长沙 410073)
0 引言
中央军委《关于提高军事训练实战化水平的意见》正式将国防建设的一系列活动推向“实战化”。所谓“实战化”,即一切国防建设活动应以“实战”为标准,并向其转化的过程。但在实际演训过程中装备可靠度只有25%,这种情况对指挥员在实战化训练和未来作战中战术制定和兵力部署都将造成严重的不利影响,甚至影响到战争的胜负和国家国防战略的制定。在实际装备系统中,应根据对抗因素的工作原理,分别分析攻击机理和防护机理,分析攻击因素的攻击性能和装备的防护性能与装备失效之间的关系。如激光驾束制导金属射流穿甲导弹与装甲车的防护系统的对抗时,导弹在驾束激光的指引下与装甲车相遇,在攻击时,通过金属射流进行穿甲,毁坏装甲车内部设备或杀伤人员从而使装甲车失效。而装甲车首先使用激光告警装置来发现照射激光,继而采用烟幕干扰和机动对驾束激光进行防护,使对方失去目标,如上述措施失效,导弹与装甲车辆相遇,则启动复合反应装甲,使导弹引信提前作用,进而使金属射流提前激发降低金属射流毁伤效果。
在对攻防模式分析、防御资源的分配、外因对系统性能影响方面,Paulson Gjerde和Slotnick[1]分析了内外两种因素随时间对系统质量的影响。司书宾等[2]对外部因素对多状态系统组部件的可靠性影响给出了定量分析。Korczak和Levitin[3,4]分析了外部因素对易受攻击的多态混联系统的影响。Levitin和Hausken[5~7]研究了暴露被攻击环境下的系统的防御资源分配方法。兑红炎等[8]给出了外部因素对部件状态概率变化的规律,分析了多状态系统中外部因素变化对系统性能的影响。
重要度理论[9]是系统可靠性理论的重要分支,是可靠性工程的重要基础理论之一,其伴随着可靠性理论和可靠性工程的发展得到了长足的进步,并在航空、航天、核能、交通等领域的可靠性优化、风险分析中得到了广泛应用。Birnbaum[10]首先提出了可靠性重要度的概念,是指系统中单个部件失效或状态改变时,其对系统可靠性的影响程度,它是系统结构和部件可靠性参数的函数。高雪莉和崔利荣[11]分析了Birnbaum可靠性重要度在系统可靠性设计、故障诊断和优化中的应用方法。吕震宙等[12]针对航空机翼设计阶段的可靠性优化问题,利用不确定重要度分析了影响机翼的不确定因素,通过对机翼结构的冗余设计来提高系统的可靠性。何爱民等[13]针对连续n中选k系统,应用马尔可夫链法对该系统进行了研究,在给出可靠度计算公式的基础上,进一步给出系统中每一个单元的重要度计算公式,从而为系统优化设计提供依据。司书宾等[14]综合考虑部件状态转移率、状态分布概率及其对系统性能的影响,给出了综合重要度理论。在系统设计、运行、维护阶段,任何行为的变化将导致部件的状态概率分布变化,部件的状态概率分布函数是关于状态转移率的函数,则部件的状态转移率对状态概率分布函数具有重大的影响。兑红炎等[15~17]充分考虑半马尔科夫过程中的状态转移情况,把综合重要度扩展到带状态转移系统和变结构系统,并分析了其变化规律及其对系统性能的影响。
在以上分析中,未将实战条件下的对抗防护因素与装备可靠性关联起来,并没有系统地研究防护因素的作用机理及多种对抗因素对系统可靠性的影响,也没有形成防护因素之间的相互关系对系统可靠性影响的评估方法。本文基于多态装备防护系统,研究部件防护层的状态变化规律,分析当部件受到攻击存活和故障时的平均性能变化机理。并给出防护层的Birnbaum重要度和综合重要度,分析当部件防护层的状态发生变化时,系统性能的变化规律;并考虑部件防护层的状态转移率,分析了在多种状态变化情况下的防护层提升对系统性能的影响。
1 多态防护系统可靠性分析
在多态装备防护系统中,所有部件都可能会受到攻击,防护能降低攻击成功的概率。如果攻击成功,那么被防护的部件将完全故障。部件j的防护层有Nj+1个不同的状态,状态空间为{0,1,…,Nj},其中0表示防护层的完全失效状态,Nj表示防护层的完好状态,状态从0到Nj的防护功能依次增加。
当部件j的防护层处于状态k时,如果部件j被攻击,那么防护层完全失效的概率为vjk。因为部件j的防护层状态从0到Nj的防护功能依次增加,所以防护层处于状态Nj时,它完全失效的概率是最小的,那么随着防护层状态k的增加,vj0≥vj1≥vj2…≥vjNj。当防护层处于完全失效状态0时,防护功能丧失,所以vj0=1。当防护层处于完好状态Nj时,那么防护层能完全抵御攻击,所以vjNj=0。则我们有1=vj0≥vj1≥vj2≥…≥vjNj=0。
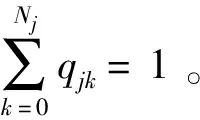
当部件j受到攻击存活时,它的性能为uj(z),当部件j受到攻击故障时,它的性能为u0(z),那么当部件j的防护层处于状态k时,部件j的性能可以表示为uj(z)(1-vjk)+u0(z)vjk。考虑部件j的所有Nj+1个状态,我们可以得到部件j的平均性能分布为
(1)
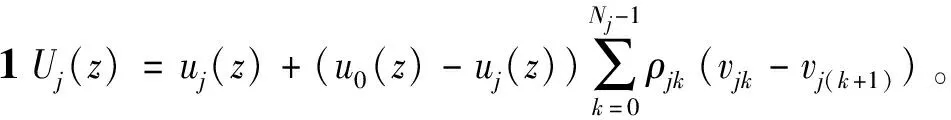
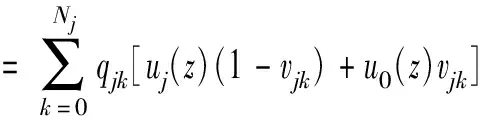
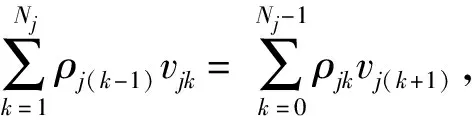
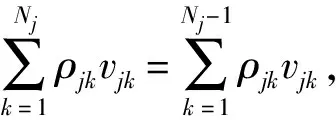
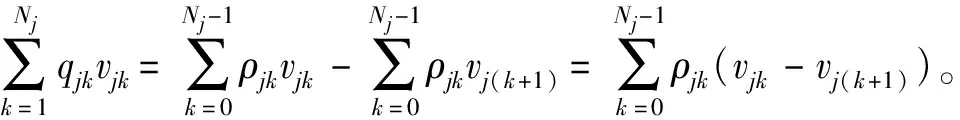
推论1如果u0(z)=uj(z),那么Uj(z)=uj(z),即部件j的平均性能等于当部件j受到攻击存活时的性能。
证明由定理1易得。
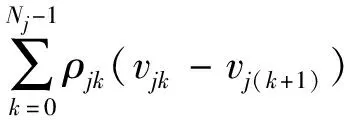
推论3如果u0(z)>uj(z),那么Uj(z)是qjNj单调递减函数,即随着部件j的防护减少,部件j的平均性能增大。
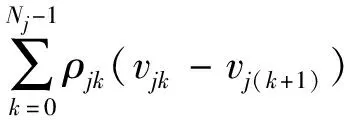
由推论2和3可得,在部件运行过程中的早期,存活部件的性能大于破坏部件的性能,此时需要增加对部件的防护;在部件运行过程的晚期,存活部件的性能小于破坏部件的性能,此时需要减少部件的防护。
2 防护重要度
假设一个系统由N个部件组成,那么系统性能G可以表示为部件性能U1(z),U2(z),…,UN(z)的函数,如公式(2)所示。
G=f(U1(z),U2(z),…,UN(z))
(2)
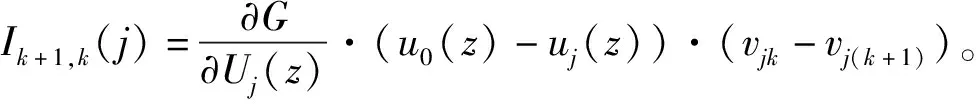
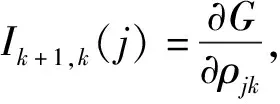
基于定理1和公式(2),我们有
肉桂醛是麝香保心丸中促血管新生最强的活性成分。韩琳等发现肉桂醛可以促进HUVECs的增殖,促进VEGF的分泌,诱导细胞的迁移,促进内皮细胞管腔形成。肉桂醛通过激活PI3K/AKT/eNOS和c-Raf/MEK/Erk1/2信号通路发挥细胞生物效应。肉桂醛能够促进斑马鱼ISVs新生,促进小鼠伤口处新血管的生成,促进VEGF蛋白表达。其肉桂醛作用效果与时间、浓度相关。吕超等发现麝香保心丸及其入血成分人参皂苷Rg3、Rh2均能够促进HUVECs增殖、迁移、管腔结构形成,其效果与时间、剂量浓度相关。高浓度麝香保心丸、人参皂苷Rg3、Rh2能够促进血管内皮细胞出芽,从而促进血管新生。
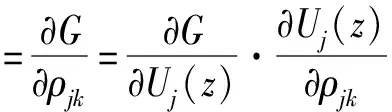
证毕。
在定理2中,针对不同的系统,G=f(U1(z),U2(z),…,UN(z))的表达式不同,以下我们以串联和并联系统为例来说明其不同。
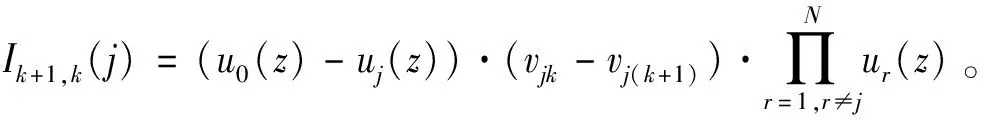
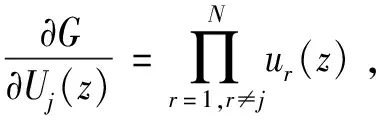

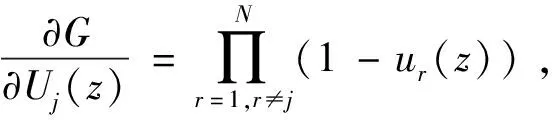
定理2表现了当部件j的防护层从状态k提升到状态k+1时,系统性能的变化。所以当部件j的防护层从状态l提升到状态m时,我们有以下推论。
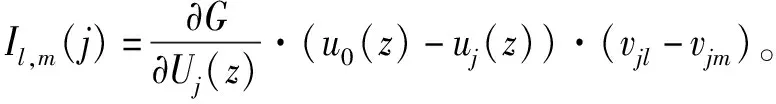
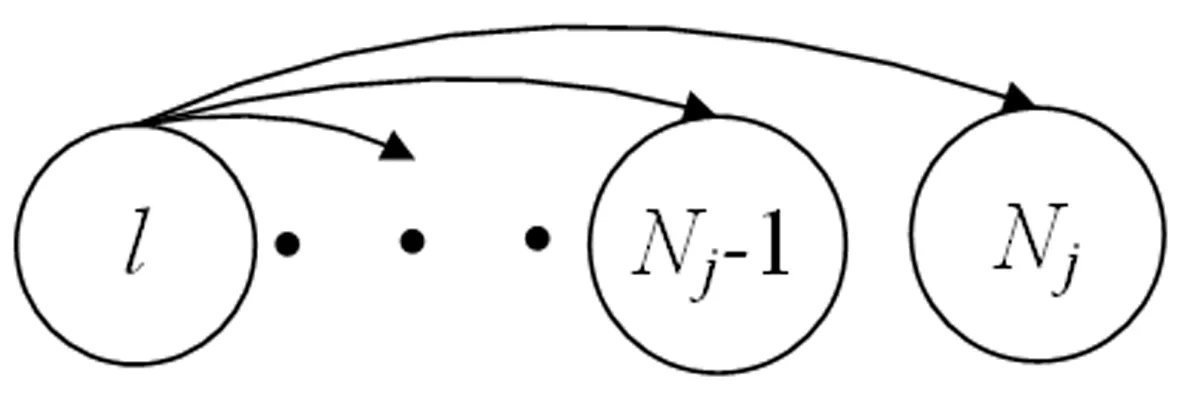
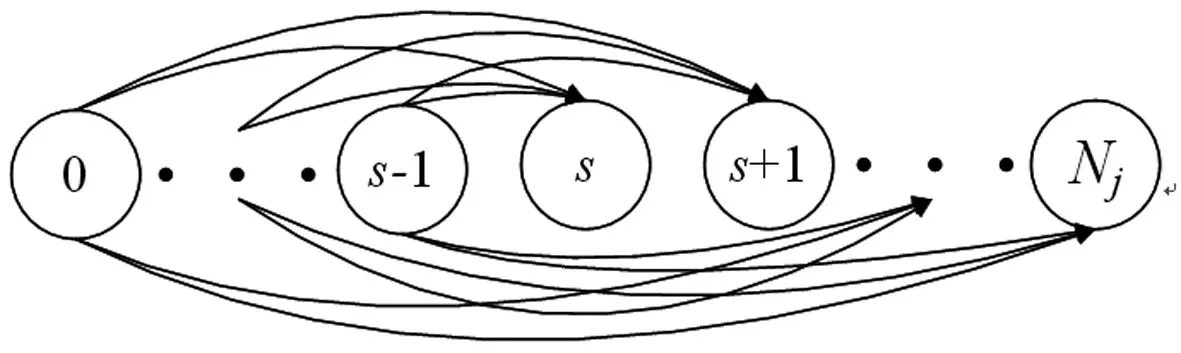
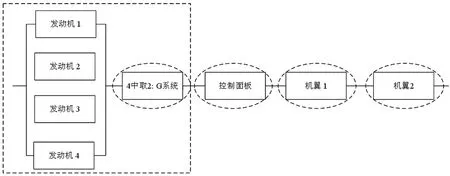
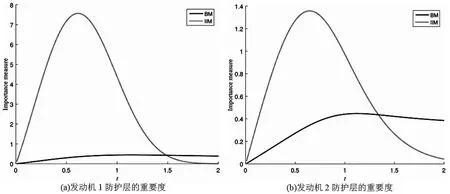
证明Il,m=Il,l+1+Il+1,l+2(j)+…+Im-1,m(j),l 证毕。 类似于综合重要度(Integrated importance measure, IIM),考虑部件j的防护层从状态l提升到状态m时的转移率,我们可以得到当部件j的防护层从状态l提升到状态m时,部件j防护层的综合重要度如公式(3)所示。 IIMl,m(j)=qjl·μl,m(j)·Il,m(j) (3) μl,m(j)表示部件j的防护层从状态l提升到状态m时的转移率。考虑了防护层的转移率,表示了单位时间内当部件j的防护层从状态l提升到状态m时,系统性能的变化。 图1 保持部件j的防护层的状态在l 以上的变化图 Il(j)表示了当部件j的防护层的状态从l到l以上转移时的系统性能变化率,可以用来衡量基于状态l的防护层提升对系统性能的影响。 假设部件j的防护层的阈值状态为s,即当防护层状态大于s时,防护层能防护对部件j的攻击,能保证部件j的工作状态,反之亦然,其状态变化如图2所示。那么系统性能变化为 图2 部件j的防护层状态变化图 Is↑(j)表示了当部件j的防护层从阈值状态s以下到阈值状态s以上转移时的系统性能变化率,可以用来衡量基于阈值状态s的防护层提升对系统性能的影响。 航空动力装置的可靠度反映了动力装置保证飞行安全的可能性。对于多发飞机而言,其动力装置为n中取k冗余子系统。一般说来,飞机所装的发动机不多于4台,现以四发直升机的动力装置为例。为保证飞行安全,4台发动机中必须有2台同时工作正常,即发动机组成了4中取2:G系统。另外发动机与控制面板、机翼等关键单元组成串联系统,其可靠性框图如图3所示。 图3 某直升机系统 在图3中,为了保证飞机的飞行安全,分别对发动机,控制系统,机翼进行防护,椭圆的虚线圈表示防护层。假设每个部件有工作和故障2个状态,部件的防护层有3个状态。部件和防护层的状态分布满足同分布的两参数的威布尔分布F(t)=1-exp[-(t/θ)γ],θ,γ>0,θ是尺度参数,γ是形状参数,同时假设部件的形状参数和尺度参数都是1。飞机最重要的是发动机,并且控制面板和机翼处于串联系统,所以这里我们以其他部件代替控制面板和机翼,防护层的形状参数和基于定理2的防护层Birnbaum重要度和公式(3)的防护层综合重要度,以下分析发动机和其他部件的防护层对系统性能的影响。因为形状参数表示了威布尔分布变化的形状,所以这里我们假设所有部件防护层满足一样的分布,尺度参数θi=1,且vj0=1,vj1=0.5,vj2=0。我们分析不同形状参数γi=0.1,γi=1,γi=3下发动机和其他部件防护层之间的BM和IIM的差别,如图4。如果部件防护层的形状参数小于1,那么转移率随着时间降低,部件防护层的BM大于IIM。如果部件防护层的形状参数大于1,那么转移率随着时间增加,部件防护层的IIM大于BM。 图4 不同形状参数的发动机和其他部件防护层之间的BM和IIM比较 四个发动机组成了4中选2:G子系统,为了分析不同发动机防护层对系统可靠性的影响,假设发动机1,2,3,4防护层的形状参数分别是γ1=3,γ2=2,γ3=1,γ4=0.1,控制面板,机翼1和机翼2的防护层形状参数是γ5=γ6=γ7=3。下面我们分析不同发动机防护层之间BM和IIM的差别,如图5所示。发动机防护层的IIM随着形状参数的增加而增加,四个发动机防护层的BM和IIM的排序为发动机1>发动机2>发动机3>发动机4,这与威布尔分布的形状参数大小相对应。 图5 不同发动机之间BM和IIM比较 本文针对多态装备防护系统的性能提升问题,基于不同的重要度变化规律,分析了部件防护层的状态变化对系统性能的影响。通过研究某直升机系统中的部件和防护层满足威布尔分布的系统可靠性变化情况,得出随着形状参数的增加,部件防护层对系统可靠性的提升增加。如果部件防护层的形状参数小于1,部件防护层的BM大于IIM。如果部件防护层的形状参数大于1,部件防护层的IIM大于BM。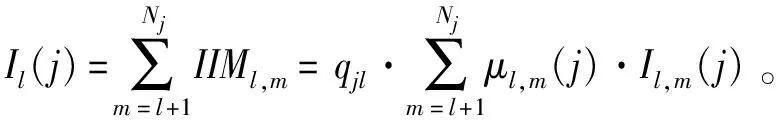
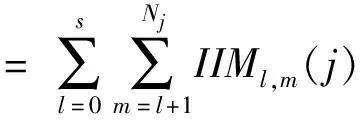
3 案例分析

4 结论