Heston随机波动率模型下带负债的投资组合博弈

杨 璐， 朱怀念， 张成科

(1.广东工业大学 管理学院,广东 广州 510520; 2.广东工业大学 经济与贸易学院,广东 广州 510520)

0 引言

投资组合问题一直是学术界研究的热点，无论从理论还是实践的角度，都具有很大的价值。Merton[1]是连续时间投资组合的先导者，其开创了“连续时间金融”这个领域。从投资的角度讲，资产负债管理问题就是投资人的财富过程扣除负债后的投资组合问题。近些年，资产负债管理问题引起了学者们的广泛注意，同时在理论界和金融机构也得到了快速发展。在目前的文献中，大部分学者采用均值-方差准则或者效用最大化准则进行研究。对于前者，Chiu和Li[2]研究了连续时间下风险资产的价格和负债过程均服从几何布朗运动的资产负债管理问题。Leippold等[3]研究了离散时间的多期资产负债管理问题。Chen等[4]、Chen和Yang[5]把Chiu和Li[2]以及Leippold等[3]的模型扩展到了Markov体制转换市场进行研究。Pan和Xiao[6]研究了随机利率和通胀风险下的资产负债管理问题。最近，一些文献开始专注时间一致的资产负债管理问题。Wei等[7]及Wei和Wang[8]研究了马尔科夫体制转换市场中的时间一致资产负债管理问题。Zhang等[9]研究了状态依赖风险规避的资产负债管理问题。对于后一种效用最大化准则，Pan和Xiao[10,11]研究了随机利率和流动约束下的最优资产负债管理问题。曾燕等[12]以最大化投资人终端时刻资产负债比率为目标，研究了连续时间框架下的资产负债管理问题，得到了最优投资策略和值函数的解析表达。在风险资产服从Heston模型方面：谢超强等[13]用指数效用准则研究了风险偏好视角的资产负债管理问题；而马娟等[14]用HARA效用准则研究了资产负债管理问题。

上述研究都是针对单个投资人展开分析的，然而现实环境错综复杂，有必要把竞争因素考虑进去，而博弈论可以对该因素进行很好地阐释。在关于投资组合微分博弈方面的文献，主要有零和微分博弈和非零和微分博弈。在零和微分博弈方面：Browne[15]是最早进行研究的；Elliott和Siu[16]研究了马尔科夫体制转换模型下保险人同金融市场之间的零和随机微分博弈问题，通过求解该博弈的均衡策略得到了保险人的最优投资策略；Mataramvura和Øksendal[17]在跳扩散金融市场中研究了风险最小化的投资组合博弈问题；杨鹏[18]研究了具有交易费用和负债的投资人与金融市场之间的零和随机微分博弈问题。然而，对于金融市场之间的非零和博弈问题：Espinosa和Touzi[19]最先研究；吴辉和马超群[20]研究了常弹性方差模型下的非零和投资组合博弈问题；Basak和Makarov[21]研究了Black-Scholes模型下的非零和投资组合博弈问题；Guan和Liang[22]研究了通胀风险下两个DC型养老金投资者的随机Nash微分博弈问题，通过最大化投资者终止时刻个人财富与竞争对手的财富之比的效用，运用随机动态规划的方法，Nash均衡策略的显式表达式被求解出来。由此，可以看出，在带负债的投资组合管理问题中,很少考虑到投资人之间的竞争因素，且目前在效用最大化准则下基于Heston模型的资产负债管理问题尚未有学者进行研究。所以，我们研究基于期望效用最大化准则带负债的投资组合博弈问题是一件有意义且富有挑战性的工作。

1 金融市场

本文是在不考虑交易成本和税收费用连续的金融市场中进行研究的。首先，我们进行了一些设定。然后，给出了金融市场中无风险资产和风险资产的价格过程。最后，给出了投资人扣除负债后的净财富过程。

1.1 基本设定

设(Ω,F,{Ft}t∈[0,T],P)是一个完备的概率空间，其中P是给出的参考概率测度，{Ft}t∈[0,T]是定义在完备的概率空间上满足常规假设的σ-域流。B(t)=(BS(t),BV(t))是在完备的概率空间上定义的一个标准的二维布朗运动，且BS(t)和BV(t)相互独立。

1.2 资产价格过程

假设金融市场中无风险债券的价格S0(t)满足如下的常微分方程

dS0(t)=rS0(t)dt,S0(0)=1

(1)

其中r为无风险利率。风险资产股票的价格过程S(t)在t时刻服从如下方程

(2)

股票价格波动的方差满足如下的随机微分方程

(3)

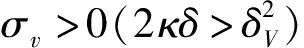
1.3 投资人的财富过程

假设金融市场中有两个投资人，记为k，k∈{1,2}。

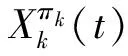
(4)

其中xk0表示投资人k的初始财富。

类似Li等[23]，假设两投资人在时间区间[0,T]内面临一个相同但不可控的与随机波动有关的外生负债L(t)，其演化过程服从如下随机微分方程

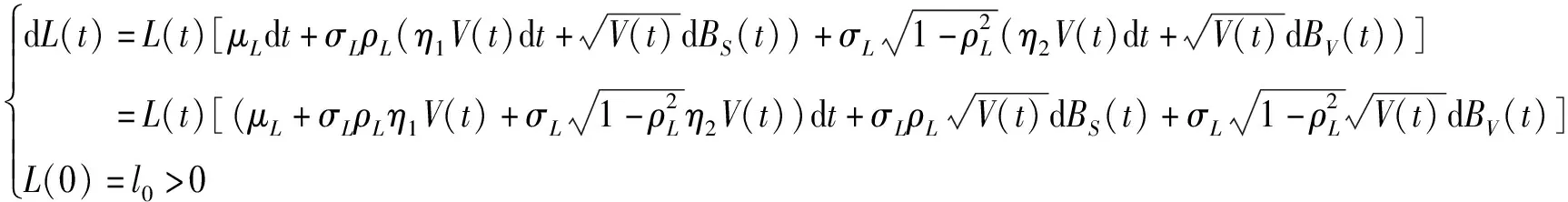
(5)

其中μL≥0和σL≥0分别为外生负债的预期增长率和波动率，ρL∈(-1,1)为负债和股票价格方差之间的相关性，η2表示风险源BV(t)的市场价格参数，l0表示初始负债。

投资过程中，投资人往往关注的是其净资产的多少。因此，扣除负债后，投资人k∈{1,2}的净资产可表示为

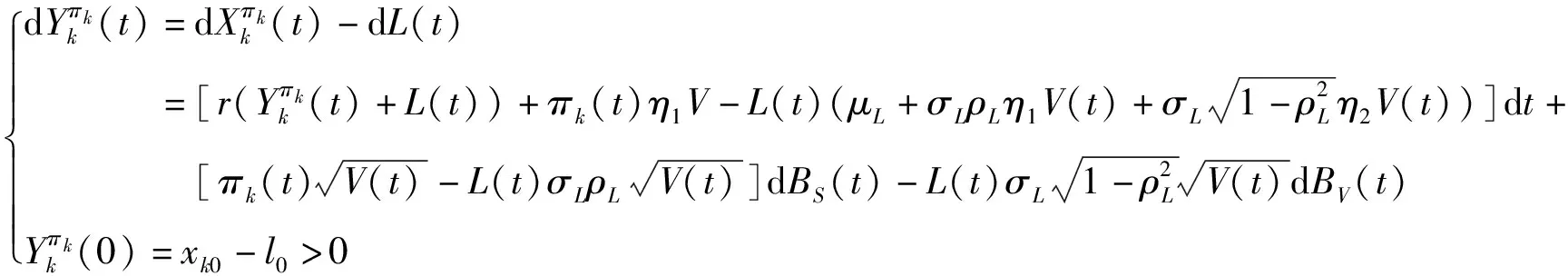
(6)

投资人k的所有可行策略πk(t)的集合记为Πk(k∈{1,2}),其所有可行策略应当满足如下的条件

①πk(t)是Ft-循序可测、右连左极的实值过程；

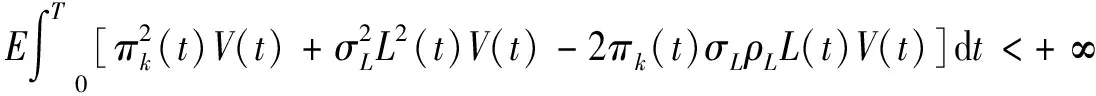
2 非零和博弈问题

下面基于期望效用准则研究非零和随机微分博弈问题。

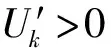
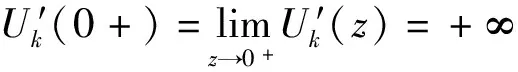
(7)

类似于Espinosa和Touzi[19]及吴辉和马超群[20]，投资人k的目标是最大化终端时刻T相对于其竞争对手相对财富的期望效用，即投资人k相对于投资人m≠k∈{1,2}的财富过程的效用如下式

=zk,L(t)=l,V(t)=v]

(8)

式(8)为投资人自身与竞争对手终端时刻财富相对差距的效用，其中投资人k对其竞争对手相关排名的看重程度记为λk∈[0,1]，也表示权重因子。

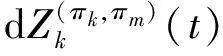
(9)

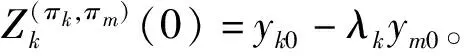
(10)

下面考虑问题(10)在幂函数下的最优问题，即投资人k∈{1,2}的效用函数形式如下

(11)

其中γk<1，γk≠0表示相对风险厌恶系数。

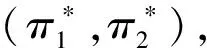
(12)

3 最优投资策略

在这一部分，我们将借助动态规划原理给出问题(12)的纳什均衡策略。定义值函数为

=zk,L(t)=l,V(t)=v]

(13)

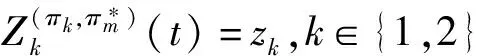
对任意的函数Ψk(t,zk,l,v)和可行策略πk∈Πk，定义生成元为

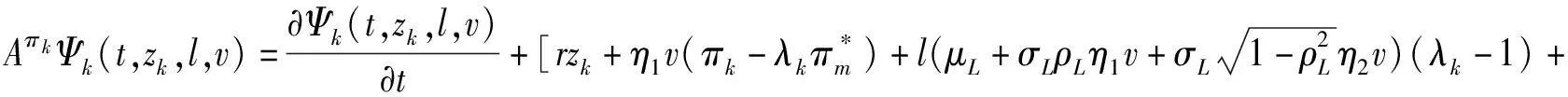
(14)

根据动态规划原理，可得生成元满足

(15)

类似Guan和Liang[22]，效用最大化问题(10)的HJB方程可表示为

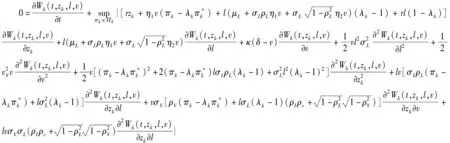
(16)

我们对上式中的πk求一阶导数，可以得到

(17)

对式(17)中的k和m赋值，解方程组可以得到

(18)

把式子(17)代入式子(16)，经过化简整理得到

(19)

设值函数为

(20)

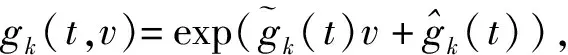
(21)

(22)

把式子(22)代入到式子(19)，经过化简整理分离变量得

(23)

式子(23)若要成立，则需要满足下式

(24)

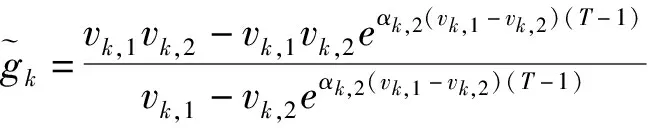
(25)

其中

(26)

综合上述分析可得下述定理。

定理1对于非零和博弈问题(10)，假设λkλ2≠1，且投资人k={1,2}的效用函数为式(11)，则投资人k={1,2}的最优投资策略和最优值函数分别为

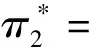
(27)

(28)

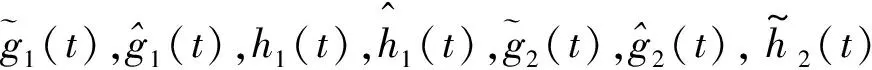
4 数值模拟

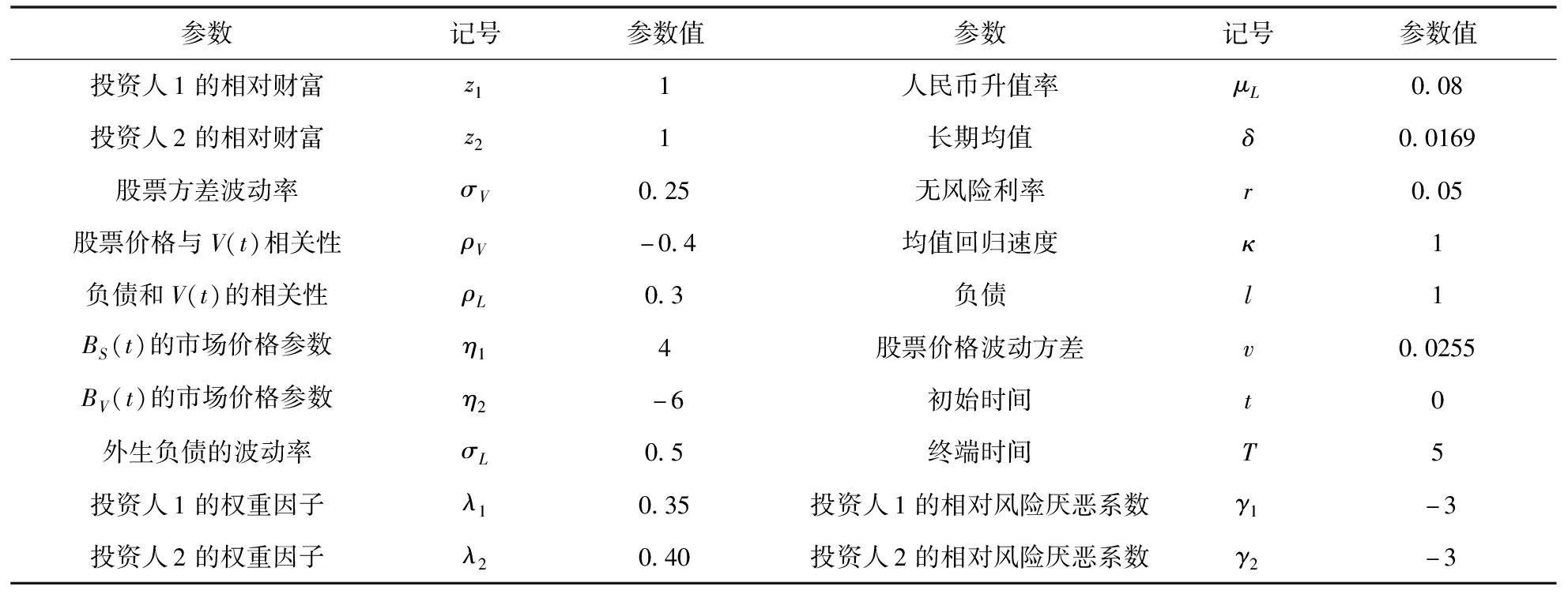
表1 基本参数的取值

由图1和图2知，投资人1的最优投资策略随着均值回归速率κ的增大而减少，随着波动系数σV的增大而增大。当ρV<0时，股票价格波动V与股票价格S的运动方向相反。股票价格波动V的平均回复速率κ越大，风险资产会具有更加不稳定的波动性，投资风险加大，故投资人1会减持股票的投资份额。当σV越来越大时，由于风险资产的波动性与其价格之间的负相关性，波动性越大，风险资产的价格就越有可能上涨。因此，随着σV的增加，投资人1将增加对风险资产的投资。投资人2的最优投资策略和投资人1的变化趋势一致。

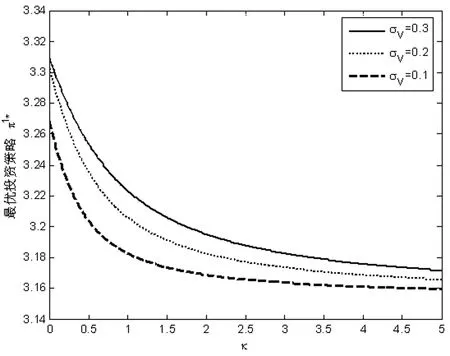
图1 κ和σV对π*1的影响

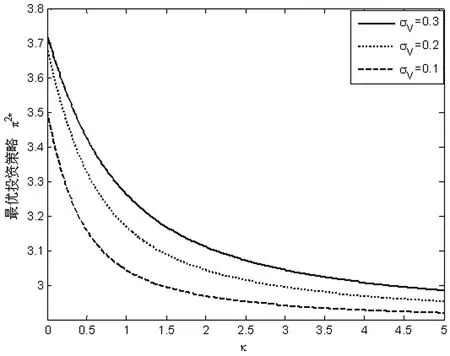
图2 κ和σV对π*2的影响

由图3和图4可以看出，相对风险厌恶系数的绝对值γk(k=1,2)越大，投资人1和投资人2减少风险资产的投资。当投资人1和投资人2的权重因子增大即与竞争对手的相关排名的看重程度不断增大时，均会加大投资。

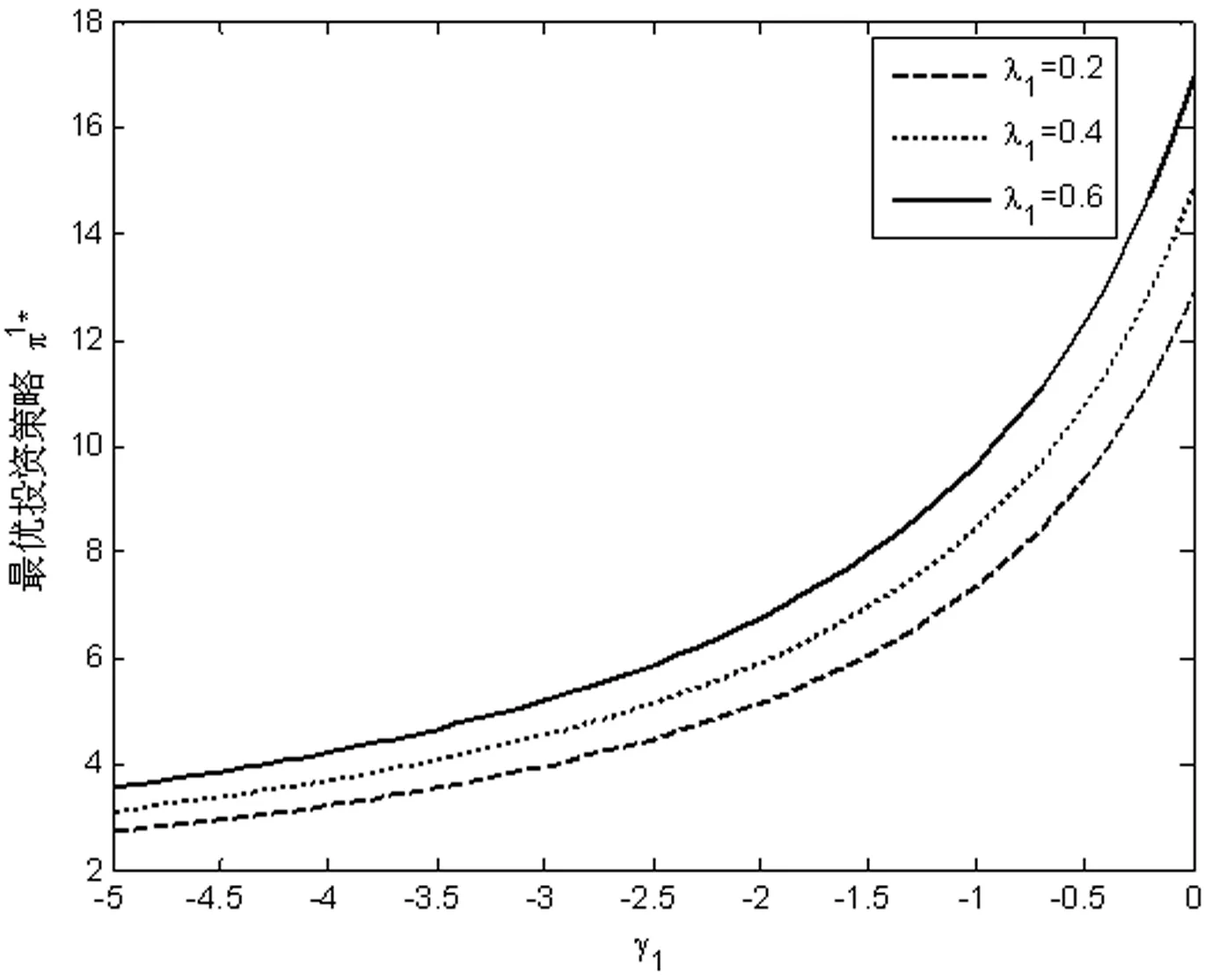
图3 γ1和λ1对π*1的影响

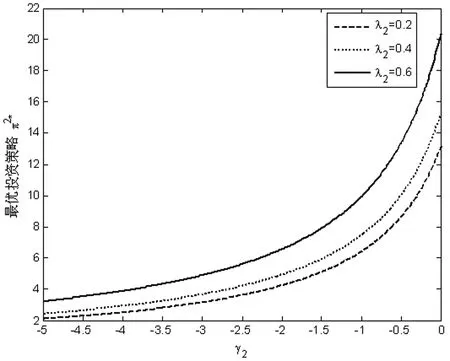
图4 γ2和λ2对π*2的影响

从图5可知，两个投资人的值函数随着的增大而减小直至趋于稳定。当逐渐增大的时候，投资人会减少投资直至不投资，故其值函数逐渐减少而趋于稳定。

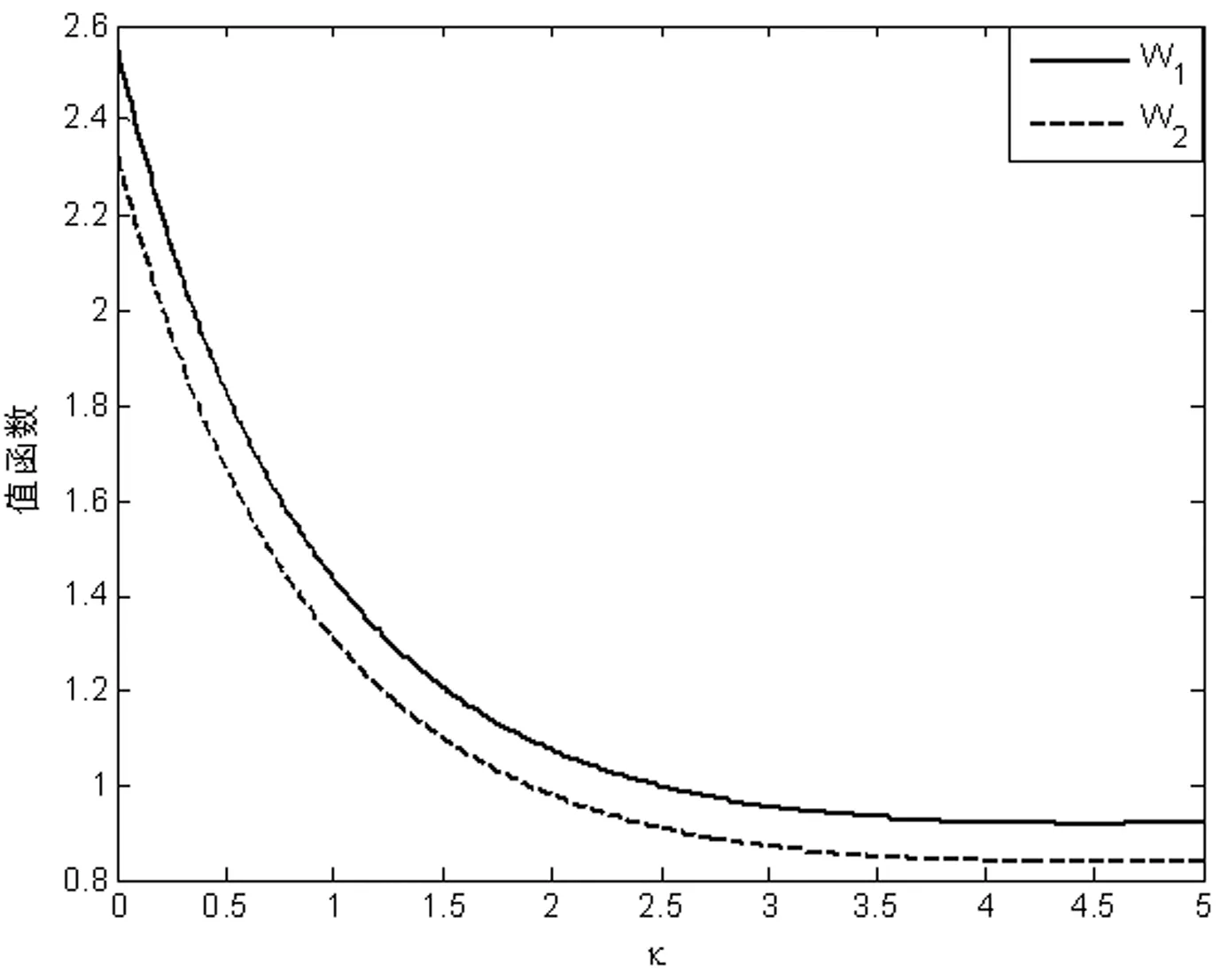
图5 κ对W1和W2的影响

5 结语

在竞争日趋激烈的投资市场，考虑投资者的相对排名也变成了一个重要的因素，所以研究资产负债投资组合的博弈问题极其重要。即研究增加负债因素的两个投资者考虑与竞争对手的相对排名时，如何在金融市场中进行投资达到效益最大。文中的非零和博弈问题被转化成投资人的期望效用最大化问题，期望效用包括投资人本身的财富和与竞争对手财富的相对差距。假设股票的收益过程服从更符合实际环境的Heston模型，通过动态规划方法，在幂函数效用框架下，推导出了均衡投资策略与值函数的显式表达。进一步，在数值结果分析中，讨论了均值回归速率κ、波动系数σV、竞争系数λ1和λ2以及相对风险厌恶系数γk等参数对均衡投资策略和值函数动态行为的影响。结果表明：(1)投资人对排名比较看重，排名越靠前，越会加大投资。(2)投资人对风险越厌恶，越会减少投资。(3)当ρV<0时，κ越大，V波动的抵消效用就越弱，股票的价格波动会加剧，会加大投资的风险，则投资人会减少风险资产股票的投资。当σV越来越大时，V波动的互补效用就越强，股票价格就会有更高的收益率，投资人会增加投资。