双目标函数约束下的停车场分配优化模型

王韩麒

(宁波宁工交通工程设计咨询有限公司，浙江 宁波 315211)

汽车保有量急剧增加，停车位供需矛盾日益凸显。特别是市中心区域因停车供给缺口较大，出行者因找不到停车位而不断巡游，加剧了区域道路的通行压力。若停车诱导系统智能化水平较低，出行者无法提前知晓停车场的使用状况，到达后车位已满，需要转移至其它停车场，耗费大量时间[1]。互联网技术的快速发展，出行者在出行前或出行中，可利用互联网及手机等智能终端，推荐最优停车场及停车位分配方案，有效改善停车难的问题[2]。国内外许多学者对停车分配进行了大量的研究。段满珍[3]等人为了弥补群体停车诱导的不足，考虑个性化的停车诱导概念及服务流程，构建了基于个性化诱导需求的停车场分配模型。陈群[4]等人以总行程时间为目标函数，考虑出行者起讫点出行及停车场周转率，对区域内停车位分配进行优化。Shao[5]等人提供了一个解决时间窗停车位共享的预约与分配模型。张硕[6]以上班族群体为研究对象，对商务区地下停车场的车位分配及定价模型进行了优化。林小围[7]等人在停车场管理中，引入合作机制，运用合作博弈理论，为出行者提供了最优车位和成本的分配方案。但是这些研究多数从出行者自身最优出发，没有考虑到智能停车诱导系统的停车分配，且只有少量利用单目标函数对停车分配方案进行约束。因此，作者拟在双目标函数的约束下，基于灰熵理论，同时兼顾考虑出行者的利益，构建停车场分配模型，求解停车场最优分配方案，以期提高区域的停车率和通行率。

1 问题的提出

假设某商业中心，附近有i个停车场，在某一时刻，处于不同位置的n辆车，同时向智能停车诱导系统申请该商业中心附近的停车场。若目的地附近没有智能停车诱导系统，则无法对车辆进行精确引导。车辆需要根据行程时间和停车成本，对停车场及停车位展开竞争。当多辆车同时竞争时，最早到达目标停车场的车辆能够优先选择停车位，最后到达目标停车场的车辆只能选择剩余的停车位或转移至其他停车场，加剧了对区域交通的影响，如图1 所示。

若目的地附近安装了智能停车诱导系统，则系统可以根据车辆的需求，针对性地制定停车场分配方案，对车辆进行快速精确的引导，提高车辆的通行率及停车场的停车率，降低停车行为对区域通行的影响，如图2 所示。

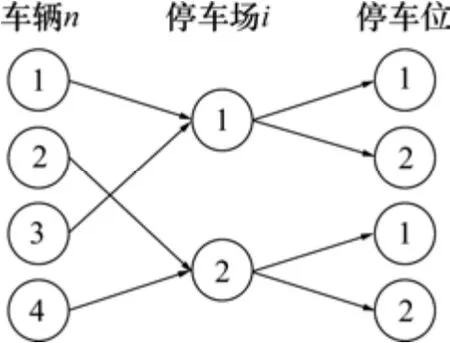
图2 有诱导系统下的停车场分配示意Fig. 2 Schematic diagram of parking lot allocation under intelligent parking guidance system

2 基于灰熵理论的停车场分配模型

构建停车场分配模型时，需明确出行者对于停车场选择的影响因素。通过对停车场的影响因素进行分析，停车场的分配，实际上是一个多属性决策问题。而基于灰熵的多属性决策模型，在属性权重已知或未知的情况下，均具有较好的应用效果。因此，采用灰熵理论[8]构建停车场分配模型。

2.1 停车场选择影响因素

在选择停车场时，影响出行者选择停车场的因素主要有4 个：

1) 行程时间toi

行程时间指的是出行者提交停车需求后，由当前位置o行驶至停车场i的时间。行程时间可由行驶时间函数(Bureau of Public Road，简称为BPR) 计算得到，同时考虑拥堵等因素，对行程时间的影响。

2) 步行距离lid

步行距离指的是出行者从停车场i，步行至目的地d的距离。通常情况下，出行者倾向于选择步行至目的地距离较短的停车场。

3) 停车场收费情况Fi

停车场收费情况指的是根据停车收费政策，不同停车场i所执行的收费标准，主要与停车场所处位置、停车场类型等有关。

4) 剩余停车位数量Qi

剩余停车位数量指的是停车场i剩余可利用的停车位的数量。当剩余停车位数量越多，越容易吸引出行者。

2.2 停车场影响因素权重的确定

停车场影响因素权重的确定，采取熵权法，其计算步骤[9]为：

1) 第i个停车场第j项决策指标的特征比重：

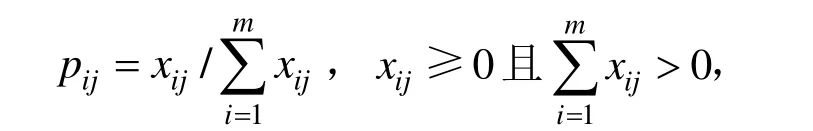
2.3 停车分配模型构建

在停车场选择中，理想决策方案e*主要为出行者根据自身情况选择的最优停车场。

4) 求解灰色关联度

以理想决策方案e*为参考序列，各具体决策方案为比较序列，计算灰色关联系数矩阵L，其计算式为：

3 双目标函数构建

在确定停车场分配方案后，需要对方案进行评价及优化。由于采用单目标函数，难以全面地衡量分配方案的优劣，存在局限性。因此，从停车诱导系统的多角度考虑，构建一个双目标函数调整和优化停车场分配方案。

3.1 系统最优目标函数

假设系统最优目标函数是进入目标区域后，所有发出停车需求的车辆，以完成整个停车行为的总耗时最小为目标。该目标函数主要目的是引导车辆快速到达目标停车场，降低因寻找泊位而造成的巡游、绕行等行为，缓解周边区域的通行压力。其函数式为：

3.2 用户最优目标函数

假设用户最优目标函数是所有车辆完成停车行为，以总停车成本最小为目标。该目标函数的主要目的是考虑出行者的停车需求，合理分配停车场，以期减少所有车辆停车成本及系统停车成本，提高停车资源的利用。其函数式为：

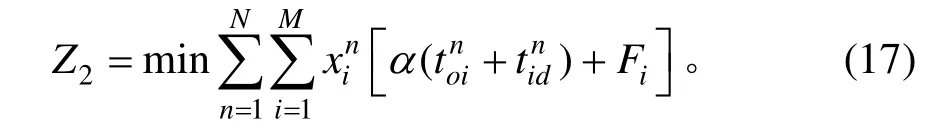
式中：α为出行者的时间价值系数；Fi为停车场i的停车费用。

根据系统最优目标函数及用户最优目标函数，从所有车辆总耗时最短的方案中，选择总停车成本最小的方案，即：在降低寻泊车辆对道路交通流的影响下，选择系统停车成本最低的停车场分配方案。

双目标函数为：

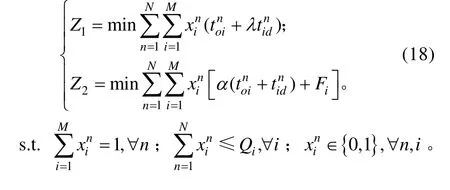
3.3 双目标函数的求解

双目标函数约束的停车场分配时，由于双目标函数之间可能存在矛盾，往往无法同时达到各自的最优解。目前，对于多目标函数优化的求解方法主要有2 种：①化多为少，将多目标函数通过简单加权的方法，简化为单目标函数进行求解。②多目标平行求解，即：并行搜索空间中的多个解。主要有粒子群算法、遗传算法等。本研究采用粒子群算法，进行模型求解。

粒子群优化算法[10](Particle Swarm Optimization,简称为PSO)是Kennedy 等人提出一种基于群体智能的全局随机搜索算法。通过迭代搜索，求解最优值。假设在一个D维的目标搜索空间中，有N个粒子组成一个群落，其中，第z个粒子表示为一个D维的向量：

3.4 停车分配模型求解流程

双目标函数约束下，停车场分配模型求解流程如图3 所示。

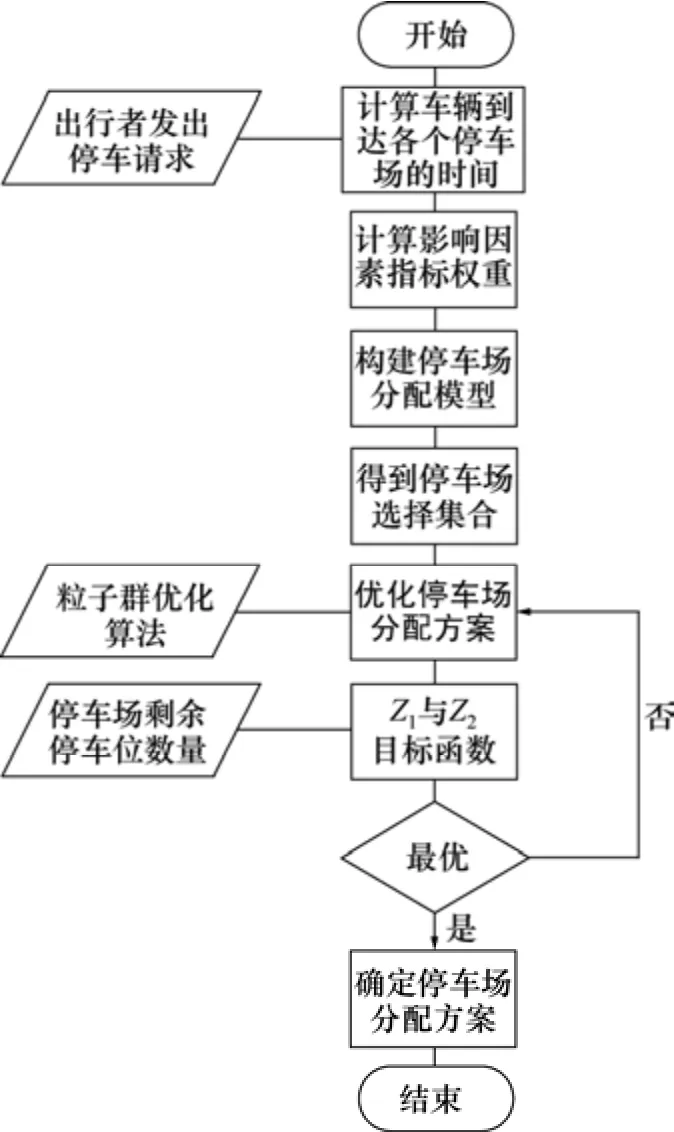
图3 模型求解流程Fig. 3 Model solution flow chart

4 算例分析

假设某商业中心，其地下停车场为P1，周边可供选择的停车场为P2及P3，如图4 所示。各个停车场的基本情况及收费情况等见表1。定义模型中α=15，λ=1.5。

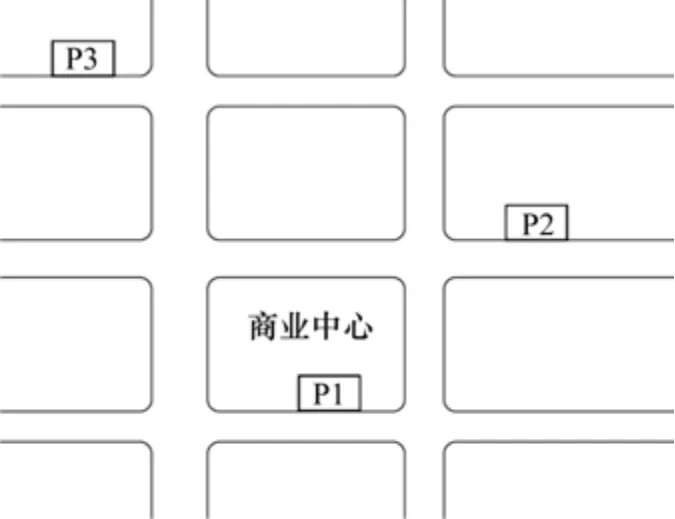
图4 路网结构Fig. 4 Road network structure

表1 停车场基本情况Table 1 Basic situation of parking lot

若有6 辆车辆同时向智能停车诱导系统发出停车申请，根据车辆的当前位置，可以得到6 辆车辆Li到达各个停车场的行程时间：

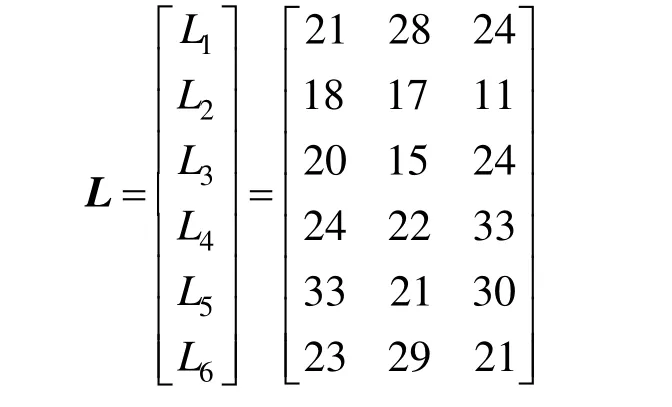
根据车辆的总行程时间及停车场各项影响因素的属性值，确定停车场选择的属性矩阵为X：

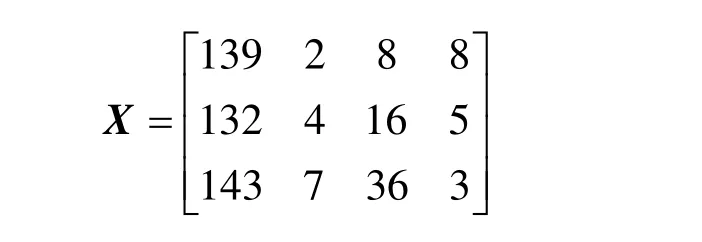
根据公式(1)计算停车场的特征比重矩阵Y。

按照公式(2)～(5)依次求解信息熵值S(pj)、输出熵值Sj、差异系数Gj，即：

然后确定停车场选择影响因素的指标权重系数为：

将影响因素的指标权重代入到构建的停车场分配模型中，根据公式(6)～(14)求解，得到各车辆停车场选择集合。

考虑到3 个停车场的剩余停车位数量均满足需求。因此，选取2 个停车场作为车辆的选择集合，即：第1 个为推荐方案，第2 个为备选方案。得到停车场初始分配方案Pre。

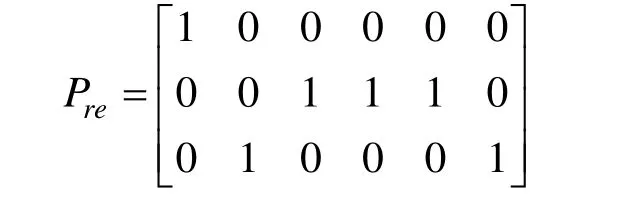
在双目标函数的约束下，借助Matlab 软件，利用粒子群优化算法，对停车场推荐分配方案进行调整和优化，得到系统最优状态下的停车场分配方案Pbest为：

在没有智能停车诱导系统的情况下，根据先到先得原则，所有车辆会优先选择P1，在P1饱和情况下，转移至其他停车场，此时，用户自身选择的停车场分配方案Puser为：

系统最优方案与用户自身选择方案各指标见表2。由表2 可知，最优方案的各项属性明显优于用户自身选择方案。最优方案中，虽然步行时间较长，但是车辆能够更快地到达目标停车场，对区域道路的通行影响更小。最优方案充分考虑出行者的利益，无论是出行者的停车成本，还是系统总停车成本，均低于用户自身选择的分配方案。

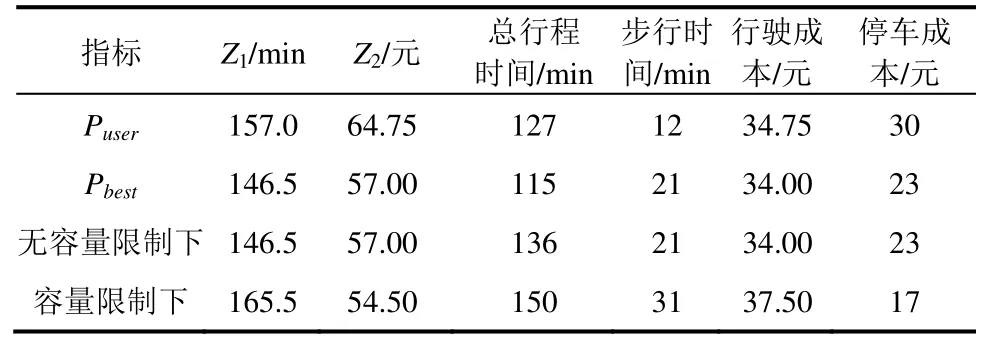
表2 停车场分配方案的指标对比表Table 2 Indicator comparison table for different parking lot allocation schemes

考虑停车场容量限制下，停车场分配结果。假设6 辆车辆同时发出停车需求时，P1剩余停车位1个，P2剩余停车位2 个，P3剩余停车位3 个。

根据停车场分配模型，计算得到停车场容量限制下的最优方案为：

对比有无停车场容量限制下的停车场分配方案，由表2 可知，容量限制下最优方案的各项属性均要高于无容量限制下的最优方案，这是当停车场剩余停车位数量大于车辆停车需求时，系统可为各车辆选取最优的停车场方案。当停车场剩余停车位数量小于车辆停车需求时，由于停车场容量限制，系统为各车辆选取停车场时，选择集合有限，因此，部分车辆的停车场选择并非最优。

5 结语

通过出行者选择停车场的影响因素，建立了双目标函数约束的停车场分配模型。基于灰熵理论，求解停车场选择集合，并根据算例，验证了停车诱导系统的最优停车场分配方案。得出的结论为：

1) 在停车场容量充足的情况下，出行者会根据自身偏好，选择最为便捷的停车场，较少考虑行程时间、费用等因素的影响。

2) 智能停车诱导系统从用户自身和系统两方面出发，并充分考虑出行者利益。通过诱导出行者到达目标停车场，从而降低对区域道路通行的影响。当停车场容量受限制时，由于出行者无法自行判断偏好的停车场是否饱和。因此，带来的绕行及巡游，增加了区域的交通拥堵。而智能停车诱导系统在有限选择集合中，为车辆选择合适的停车场。虽然部分车辆的选择并非最优，但从整体来看，无论是出行者的停车成本，还是系统总停车成本，均低于用户自身选择的分配方案。

3) 因所有的出行者均假设为同质，没有考虑出行者的选择偏好对于停车场选择的影响。同时，行程时间的计算简单，没有考虑道路拥堵程度和拥堵时段对行程时间的动态影响。未来有待进一步研究，如：利用聚类分析方法，确定出行者的选择偏好和道路行程时间动态变化对停车场分配的影响。