基于Pythagorean模糊熵的风险型决策方法——考虑后悔与失望规避

李 娜，高雷阜，王 磊

(1.辽宁工程技术大学 运筹与优化研究院,辽宁 阜新 123000; 2.辽宁工程技术大学 基础教学部,辽宁 葫芦岛 125105)

0 引言

多属性决策是指具有多个属性的有限方案排序和选择问题，其理论与方法在经济、管理、工程和军事等诸多领域具有广泛的应用[1]。自Yager[2,3]提出了Pythagorean模糊决策以来，众多学者对Pythagorean模糊多属性决策进行了研究。Peng[4]定义了Pythagorean模糊集一些新的相似测度和距离测度，并将他们应用到Pythagorean模糊决策环境。Chen[5]构建了Pythagorean模糊VIKOR决策模型。刘卫锋等[6]提出了Pythagorean模糊Hamacher加权平均算子，Pythagorean模糊Hamacher有序加权平均算子，Pythagorean模糊Hamacher加权几何算子以及Pythagorean模糊Hamacher有序加权几何算子，并应用到多属性决策问题。Wei等[7]提出了一些Pythagorean模糊幂集结算子，李娜等[8]提出诱导型广义Pythagorean模糊Choquet积分算子，并将其应用到多属性群决策问题。考虑到隶属度和非隶属度的相互作用，Wei[9]提出了交互式Pythagorean模糊集结算子。Biswas 和 Sarkar[10]将传统的TOPSIS方法拓展到Pythagorean模糊决策环境。李娜等[11]提出了区间Pythagorean模糊AQM决策方法。Garg[12]提出对数形式的Pythagorean模糊集结算子并应用到多属性决策问题，Liu等[13]提出了带有可能度的区间Pythagorean模糊决策方法。李鹏等[14]在Pythagorean模糊群决策环境下，提出了一种灰色关联决策方法。Ilbahar等[15]提出了Pythagorean 模糊AHP决策方法，并用于健康安全评价。

作为决策理论与方法中的重要内容，风险型多属性决策问题考虑了不同状态的概率可预估，备选方案的选择具有一定的风险的排序问题。考虑到决策者的心理行为，谭春桥和张晓丹[16]提出了基于后悔理论[17,18]的风险型决策方法。张浩[19]在应急方案选择与调整过程中既考虑了决策者后悔行为也考虑到了失望行为[20,21]。目前，在Pythagorean模糊环境下的风险型决策方法较少，Liang等[22]基于前景理论提出了Pythagorean模糊TODIM多属性决策方法，Peng等[23]分别利用前景理论和后悔理论研究了Pythagorean模糊风险型多属性决策问题，并利用算例对两种方法进行比较分析。

模糊熵刻画了模糊集的不确定程度，Joshi和Kumar[24]提出了直觉模糊熵，刻画了直觉模糊集的不确定程度，Li等[25]研究了直觉模糊集的相似测度和熵的关系，Hussain和Yang[26]提出了犹豫模糊熵，刻画了犹豫模糊集的不确定程度，王坚强等[27]提出了语言D数模糊熵，刻画了语言D数的不确定程度。目前，模糊熵并未完全扩展到Pythagorean模糊集中[10,28]。

风险决策过程中决策者常常表现出风险规避、后悔规避和失望规避等行为，其中，后悔行为是由于备选方案比决策者主观选择的方案要好时产生的；失望行为是同一选择有多个可能结果时，外在环境导致决策者选择的实际结果较差时产生的[29]。决策者在选择备选方案时会追求后悔最小化或失望最小化，因此，风险决策需要考虑决策者的后悔与失望行为[19]。鉴于此，本文考虑到决策者的后悔与失望规避心理行为，针对属性值为Pythagorean模糊数的风险型多属性决策问题进行探究，定义了新的Pythagorean模糊熵，由此获得不同状态下属性权重，并通过加权求和获得综合属性权重。同时将决策者的后悔心理和失望心理行为特征加以考虑，提出一种基于Pythagorean模糊熵的考虑后悔与失望规避的决策方法。最后，通过算例分析验证了本文方法的有效性和优点。同时，分析了后悔规避系数δ和失望规避系数τ对决策结果的影响。

1 预备知识

1.1 Pythagorean模糊集

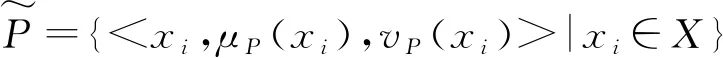
若μQ(xi)≥vQ(xi),则μP(xi)≥μQ(xi),vP(xi)≤vQ(xi);

若μQ(xi)≤vQ(xi),则μP(xi)≤μQ(xi),vP(xi)≥vQ(xi)。

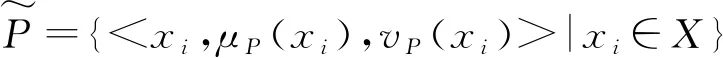
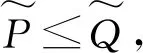
1.2 后悔与失望理论

后悔理论是由Bell[17]和Loomes等[18]分别提出来的，基本思想是决策者会将自己考虑选择方案的结果与其他方案可能获得的结果进行比较，如果发现选择其他方案可以获得更好的结果，那么其心中会感到后悔；反之，则会感到欣喜。在悔理论提出后Bell又提出了失望理论[20]，其基本思想是决策者会把实际的决策结果与期望进行比较，当实际决策结果小于期望值时，决策者会感到失望；反之，则会感到愉悦。在决策过程中，决策者会对潜在的结果有所预期，并且避免选择会使其感到后悔和失望的方案[17,18,20]，即决策者在决策过程中是后悔和失望规避的。

令x1，x2和x3分别表示选择方案A1，A2和A3所能带来的结果。依据后悔理论和失望理论[17,20]，决策者的感知价值由三部分组成，即关于当前选择方案的效用值、后悔-欣喜值和失望-愉悦值，于是决策者对方案A1的感知价值[19,21]为

u(x1,x2,x3)=u(x1)+kR·R(Δv)+kD·D(Δθ)

(1)

其中，kR和kD分别表示后悔和失望对决策的影响程度。Δv=v(x1)-v(x2)，v(x1),v(x2)分别表示决策者从选择备选方案A1和A2的结果中获得的效用值，R(Δv)表示后悔-欣喜值，当R(Δv)>0时，R(Δv)为欣喜值，表示决策者对选择方案A1而放弃选择方案A2感到欣喜的值； 当R(Δv)<0时，R(Δv)为后悔值，表示决策者对选择方案A1而放弃选择方案A2感到后悔的值；D(Δθ)表示失望-愉悦值，Δθ=v(x1)-v(x3)，v(x1),v(x3)分别表示决策者从选择备选方案A1和A3的结果中获得的效用值，当D(Δθ)>0时，D(Δθ)为愉悦值，表示决策者对选择方案A1而放弃选择方案A3感到愉悦的值；当D(Δθ)<0时，D(Δθ)为失望值，表示决策者对选择方案A1而放弃选择方案A3感到失望的值。

2 模型的构建与方法设计

2.1 决策问题描述

表1 决策矩阵

2.2 Pythagorean模糊风险型决策方法

针对属性值由Pythagorean模糊数表示的风险型多属性决策问题，下面利用后悔与失望理论提出一种新的决策方法。基本思路如下：

(2)

(3)

其中，α为决策者的风险规避系数，满足0<α<1。α越大，则相同属性值的效用值越大，表明决策者对该属性的偏好程度越大。

(4)

若x服从正态分布，则

i∈M,j∈N,t∈H

(5)

(6)

R(Δv)=1-exp(-δΔv)

(7)

其中，δ为决策者的后悔规避系数[16]，δ越大，决策者的后悔规避程度越大，Δv为两个方案的效用之差。

根据式(7)，确定状态St下方案Yi针对属性Cj相对于理想点的后悔-欣喜值，表达式如下:

(8)

再次，计算每个方案下，各个状态针对各个属性相对于理想点的失望值。 这里，首先确定失望-愉悦函数D(Δθ)，由于决策者对于失望和愉悦都是风险规避的，因此，函数D(Δθ)是单调递增的凹函数[19,20]，满足D′(Δθ)≥0且D″(Δθ)≤0,D(0)=0。本文采用如下的函数[19,21]:

D(Δθ)=1-τΔθ

(9)

其中，τ为决策者的失望规避系数[19]，τ越大，决策者的失望规避程度越大。

根据式(9)，确定方案Yi下状态St针对属性Cj相对于理想点的失望-愉悦值，表达式如下

(10)

注1式(8)中的理想点是在同一状态同一属性下，由不同方案的决策信息相互比较确定的；式(10)中的理想点是在同一方案同一属性下，由不同状态所对应的决策信息相互比较确定的。

在上述基础上，根据式(1)建立状态St下方案Yi针对属性Cj的感知效用

(11)

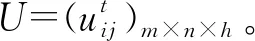
最后，利用属性权重获得方案Ai的综合感知效用:

(12)

其中，pt为状态St发生的概率，ωj(j∈N)为属性Cj的权重，通常情况下属性的权重信息并不已知。依据综合感知效用ρi对方案进行比较排序，确定最优方案。

2.3 求解属性权重

由于决策情形的复杂性，属性权重信息常常难以确定。在每一状态下，属性信息越模糊越不确定，表明决策者对该属性的了解程度相对越少，则赋予较小权重。反之，则赋予较大权重。而这种属性信息的模糊性和不确定性可以用模糊熵来衡量。

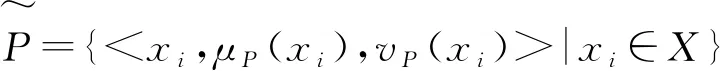
(13)

下面，利用Pythagorean模糊熵确定属性权重。

(14)

进一步，简单的加权得到属性Cj的权重

(15)

其中，由于pt为状态St发生的概率，t∈H。

2.4 决策方法步骤

Step5利用式(14)-(15)求解属性权重ω=(ω1,ω2,…,ωn)。

Step6利用式(12)得到备选方案的综合感知效用ρi(i∈M)，依据ρi越大，方案越佳，确定最佳方案。

3 算例分析

某计算机图书出版社要出版一本畅销书(改编自文献[23])。有4个方案可供选择，分别为：《机器学习》A1；《数据挖掘》A2；《大数据》A3；《深度学习》A4；主要评价指标(属性)有：普及性C1；创新性C2；图书价值C3。根据市场预测，在出版期间有3种可能的状态S={S1,S2,S3}分别表示好、中和差，对应发生的概率分别为p1=0.2,p2=0.5,p3=0.3。该出版社给出4个备选方案关于3个评价指标的评价结果如表2所示。在上述条件下，试确定最佳的出版书籍。

表2 决策矩阵

3.1 计算过程

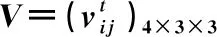
表3 效用值矩阵

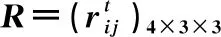
表4 后悔-欣喜值矩阵

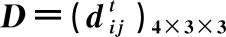
表5 失望-愉悦值矩阵

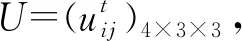
表6 感知效用矩阵

Step5利用式(14)～(15)求得属性权重ω=(0.4100,0.3006,0.2894)T。

Step6利用式(12)求得备选方案的综合感知效用值:ρ1=0.4874,ρ2=0.4768,ρ3=0.4958,ρ4=0.4957。由于，ρ3>ρ4>ρ1>ρ2，获得方案排序：A3≻A4≻A1≻A2。故，最佳方案为A3，即最佳出版书籍为《大数据》。

3.2 参数δ和τ的变化对决策结果的影响

下面，讨论后悔规避系数δ和失望规避系数τ对决策结果的影响。

首先，固定一个参数，分析另一个参数的变化对决策结果影响。固定后悔规避系数δ，取δ=0.3，分析失望规避系数τ在区间[0.1,0.9]变化，获得排序结果如表7所示。

表7 δ=0.3时不同τ对应的排序结果

由表7可以看出，失望规避系数τ取较小值时，如：0.1,0.2，排序结果为：A4≻A3≻A1≻A2，当失望规避系数τ超过0.2后，排序结果变为A3≻A4≻A1≻A2。方案A3和A4的排序发生改变。

接下来，固定失望规避系数τ，取τ=0.3，分析后悔规避系数δ在区间[0.1,0.9]变化，获得排序结果如表8所示。

表8 τ=0.3时不同δ对应的排序结果

由表8可以看出，后悔规避系数δ取较小值时，如：0.1,0.2，排序结果为：A4≻A3≻A1≻A2，当后悔规避系数δ超过0.2后，排序结果变为A3≻A4≻A1≻A2。同样，方案A3和A4的排序发生改变，如图1所示。

图1 不同δ下的综合感知效用

由图1反映出，随着后悔规避系数δ的增加，4个方案的综合感知效用都在递减，方案A1和A2的排序不变，方案A3和A4排序发生改变。

图2 4个决策区域

接下来分析当2个参数δ，τ同时变化对决策结果的影响。经分析计算得，在(τ,δ)的允许取值范围G={0<τ<1,0<δ<1}内，存在4个不同的区域G1={0<τ≤0.193,0<δ<1},G2,G3,G4={0.37≤τ<1,0<δ<1}，如图2所示。其中，区域G2和G3的分界曲线表达式为δ=-0.0002335e18.08τ+7.824e-10.66τ,0.193<τ<0.37，进一步的分析获得如下结果：

当参数(τ,δ)在区域G1或G3变化时，排序结果为：A4≻A3≻A1≻A2，最佳方案为A4，当(τ,δ)在区域G2或G4变化时，排序结果为：A3≻A4≻A1≻A2，最佳方案为A3。表明当失望规避系数τ较小且满足0<τ<0.193时，无论后悔规避系数δ取多大的值，排序结果始终为：A4≻A3≻A1≻A2。当失望规避系数τ较大且满足0.37≤τ<1时，无论后悔规避系数δ取值多小，排序结果始终为：A3≻A4≻A1≻A2。

当参数(τ,δ)按照关系式δ>-0.0002335e18.08τ+7.824e-10.66τ,0.193<τ<0.37变化时，排序结果为：A3≻A4≻A1≻A2，而当参数(τ,δ)按照关系式δ<-0.0002335e18.08τ+7.824e-10.66τ,0.193<τ<0.37变化时，排序结果为：A4≻A3≻A1≻A2。 说明参数(τ,δ)的变化对决策结果具有重要影响。实际决策过程中后悔规避系数δ和失望规避系数τ的取值通常都较大些，这样避免决策过程中出现较大可能的后悔行为和失望行为。

3.3 对比分析

(1)可行性分析

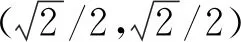
表9 前景决策矩阵

其中， 参数α=β=0.88,θ=2.25,γ=0.61,δ=0.72。取属性权重ω=(0.4100,0.3006,0.2894),利用Pythagorean加权平均算子获得每个方案的综合前景值：V1=(0.3028,0.0055),V2=(0.3412,0.0034),V3=(0.3500,0.0042),V4=(0.3323,0.0062)，在此基础上计算得分函数[23],S(V1)=0.5743,S(V2)=0.5965,S(V3)=0.6020,S(V4)=0.5910，进而获得方案排序：A3≻A2≻A4≻A1，最佳方案为A3，与本文的一致，表明本文方法的可行性。

(2)优点分析

本文的决策方法既体现了后悔规避又体现了失望规避，相比文献[5,10,14,15]中的决策结果更符合决策者的心里特征，同时相比文献[19,23,29]，本文方法更适合复杂的模糊决策环境。具体分析如表10所示。

表10 不同方法特征比较

4 结论

本文针对属性权重完全未知且属性值为Pythagorean模糊数的风险型多属性决策问题进行了研究，提出一种基于Pythagorean模糊熵的考虑决策者后悔与失望规避心理行为的决策方法。该方法的特点是决策过程中同时考虑了决策者可能出现的后悔行为与失望行为，更符合决策者的心理特征。运用Pythagorean模糊熵获得的属性权重减少了权重确定的主观性，而且该Pythagorean模糊熵既考虑了隶属度与非隶属度的偏差对其影响，又考虑了犹豫度对其影响。算例分析表明了本文决策方法的可行性和优点，同时也说明后悔与失望规避系数(τ,δ)的变化对决策结果具有重要影响。