装备维修器材生产路径双目标问题优化决策方法研究

滕尚儒，何成铭，丛 彬

(1.陆军装甲兵学院 装备保障与再制造系,北京 100072; 2.陆军装备部信息保障室,北京 100072)

0 引言

装备维修器材供应保障是装备保障工作的重要组成部分，其基本职能是弥补器材供需之间在空间上和时间上的不一致，以保证平时和战时器材供应的不间断[1]。其主要任务涉及到生产和库存计划的制定、运输方式和运输工具的合理选择、配送路径规划等[2]。研究合理地制定生产、库存及配送计划，使得供应链上总成本最低，该优化问题被称为生产路径问题(production routing problem，PRP)。PRP一般研究：已知各客户点物品的初始存储量、每天消耗规律、最大库存能力，以及生产厂家的生产、库存水平、配送车辆运输能力，需要确定生产厂家的生产策略、客户的库存策略，以及给各客户配送物品的时间、数量、配送路径，以保证在各客户不缺货的情况下，规划周期内的总成本最小。

在一般的单目标PRP中，最小化总成本或最大化总利润是最常见的优化目标，但在实际问题中，决策者通常需要用多个目标来比较，而这些目标有时不甚协调，甚至是矛盾的。同样对器材供应保障工作而言，如果只考虑成本，而对部队的需求反应滞缓，不能在一个合理的期限内，将部队所需的器材送达目的地，其后果也许是相当严重的，提出申请的部队会因此失去应有的战斗力，甚而整场战争也会因此而失利。同时，现代战争具有节奏快、攻防转换频繁的特点，部队用户往往对器材保障的精度有严格要求。超过部队用户的实际需求量，会增加部队用户的仓储成本，浪费人力物力，而且过多的辎重会影响部队的机动性，使部队受到攻击的风险增大。这种情况下，衡量一个器材保障优化方案的好坏往往难以只用经济指标来判断。器材保障能否在保证经济效益的前提下，在恰当的时间和恰当的地点为部队用户提供恰当品种、数量器材，亦即精确保障理论中的“适时、适地、适量”保障[3]，成为保障部队用户实现军事效益的关键。

装备维修器材PRP优化涉及到时间、经济、效用等诸多目标，这种多目标、多约束、多要求、动态性等特点，使得传统优化方法和模型的应用受到很大限制[4]。关于多目标优化问题，目前国内外有较多研究。龚延成[5]在分析战时物流运输路线选择时，综合考虑了安全性、时效性和经济性三个决策目标，通过无量纲化转化成单目标决策问题，并用最短路径方法求解最优路径。石玉峰[6]针对目标的模糊性，建立了基于时间、风险和保障代价三个方面的模糊多目标决策模型，通过消弧和最小费用路法求得了最优解。Amorim和Almada-Lobo[7]研究了一个带时间窗的双目标生产运输问题，同时优化了运输费用和用户满意度。

本文以总成本最小为主要目标和订单精准执行率最高为辅助目标，建立装备维修器材PRP双目标优化决策模型，并开发一个基于ε-约束法的两阶迭代启发式算法进行求解之后采用一种模糊逻辑决策法帮助决策者选择折中最优解，最后利用实例验证提出的模型与算法。

1 问题描述与建模

1.1 问题描述与符号说明

假设用有向图G=(N,A)表示配送网络，其中N={0,1,…,n}表示节点集，A为弧集。节点0表示装备维修器材生产工厂，其库存能力记为U0，最大生产能力记为C。工厂可生产单品种器材，并可调用一组容量为V的相同类型车辆K={1,2,…,|K|}。图G中分布有一组部队用户R={1,2,…,n}，每个部队用户i∈R的最大库存能力为Ui，在计划期T={1,2,…,|T|}内，对器材的需求具有确定性和时变性。

装备维修器材PRP的双目标优化决策问题是指在满足各部队用户需求的前提下，对生产计划、库存计划和运输路径规划进行整合，以最小化生产、库存、运输总成本，同时最大化订单精准执行率。其中，订单精准执行率是器材精确保障中重要的指标，它包含多方面因素，如供货准时率、数量准确率、质量合格率、资料齐备率等。本文利用每个时间段结束时部队用户的库存持有量与该阶段实际需求量的比值来表示订单精准执行率，这里需要注意的是，该比值越小，表示订单精准执行率越高。

每阶段需要决策的问题如下：(1)工厂生产多少；(2)给每个部队用户交付多少；(3)工厂和每个部队用户各需持有多少库存；(4)如何确定最佳运输路径。

为公式化该问题，定义了以下参数和变量：

cij：(i,j)∈A之间的运输成本；

at：阶段t∈T的单位生产成本；

bt：阶段t∈T的生产准备成本；

C：工厂的生产能力；

gi：i∈N的初始库存；

Ui：i∈N的库存能力；

hi：每阶段节点i∈N的库存成本；

V：车辆最大允许装载量；

引入决策变量如下：

pt：阶段t工厂生产的器材量；

wt：0-1决策变量，若阶段t工厂启动生产，则wt=1，否则其值为0；

为了简化建模过程，在上述供应保障过程描述的基础上，做出如下几点假设和说明：(1)每辆车在完成每次配送任务后返回工厂；(2)每阶段每辆车至多执行一次配送任务；(3)每阶段每个部队用户仅能由同一车辆为其提供一次服务。

1.2 模型建立

本文提出的装备维修器材PRP双目标优化决策模型P表示如下：

目标函数：

(1)

(2)

约束条件:

(3)

(4)

(5)

pt≤Cwt,∀t∈T

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

pt≥0,∀t∈T

(14)

(15)

(16)

wt∈{0,1},t∈T

(17)

(18)

(19)

其中，目标函数(1)由生产、库存和运输成本三部分组成；目标函数(2)表示最大化订单精准执行率，这里目标值越小，订单精准执行率越高。式(3)～(5)确保工厂和部队用户之间的库存守恒；式(6)确保工厂每阶段的生产量不超过工厂最大生产能力；式(7)限制了每个节点的最大库存；式(8)确保车辆在配送过程中的实际载货量不超过其最大允许装载量；式(9)表示只有部队用户被访问时才允许车辆交付器材；式(10)表示每个部队用户至多被一辆车访问；式(11)表示车流量守恒，即车辆到达一个节点后必须从该节点离开；式(12)确保每辆车每阶段至多执行一次配送任务；式(13)消除了子回环，避免了子回路解产生；式(14)～(19)界定了决策变量的范围。

2 求解算法

从上述的模型可以看出，装备维修器材PRP双目标优化决策问题是一个复杂的最优化问题。为此，本文开发了一个基于ε-约束法的两阶迭代启发式算法(ε-constraint-based two-phase iterative heuristic,ε-CTIH)并利用模糊逻辑决策法，帮助决策者在两个目标之间找到平衡点，实现双目标函数在给定区域上的最优化。

2.1 双目标优化问题原理

一般的双目标优化问题可以用如下公式表示：

minf1=φ(x)

(20)

minf2=ω(x)

(21)

约束条件：

x∈X

(22)

式中，f1和f2表示两个可能矛盾的目标，即，可能不存在使和同时达到最小的解；X是双目标优化模型的约束集，φ(x)和ω(x)分别对应于两个目标函数。

若φ(x)≤φ(x′)且ω(x)≤ω(x′)，称一个可行解x∈X不劣于另一个可行解x′∈X，当且仅当x不劣于x′，同时两个不等式中至少有一个不等式取严格小于号，则称解x占优于x′，记为x′x。如果不存在其他x′∈X，使得x′x，则称x∈X是多目标优化模型的Pareto最优解，或称为非劣解，其对应的目标值φ(x)和ω(x)形成一个Pareto最优点，在目标函数可行解空间里所有的未被占优的点构成Pareto前沿。综上，Pareto解集可定义为PS={x∈X|x为Pareto最优}，Pareto前沿定义为Pf={(φ(x),ω(x))|x∈PS}。

2.2 ε-约束法

ε-约束法的基本思想是通过适当处理将最初的多目标问题转化为一系列单目标问题。首先求得目标函数ω(x)的最优值ε，之后将其转化为ω(x)的约束条件，即在ω(x)≤ε约束下，寻找另一目标φ(x)的最优值，从而获得一组Pareto解。对于给定的ε值，单目标问题M(ε)描述如下:

min{φ(x)|ω(x)≤ε,x∈X}

(23)

求解该问题可得x*(ε)∈X，f1(ε)=φ(x*(ε)),f2(ε)=ω(x*(ε))<ε。这里可以很容易地证明，对任意x∈PS，存在一个ε，使得x=x*(ε)。因此，然后逐渐增加或减少ε的值并以此为约束求得φ(x)的最优值，通过多次求解，逐渐求得多组在ω(x)不同值情况下φ(x)的Pareto解，获得Pareto解集PS，便是初始问题的最优解集，决策者可以根据偏好从中选择理想的Pareto解。对于本文研究的问题，可将第二个目标订单精准执行率转化为一个约束条件，得到如(23)所示的单目标模型M(ε)。

(24)

(25)

(26)

(27)

理想情况下，通过列举ε的所有可能取值来求解一系列M(ε)，可以生成精确的Pareto前沿。但由于参数ε的连续性，该步骤需要求解大量复杂且耗时的M(ε)，可行性不强。实践中，决策者期望在合理的计算时间内获得一些有代表性的Pareto解来构成近似Pareto前沿AF。因此，本文提出了一个基于ε-约束的两阶迭代启发式算法ε-CTIH来获取近似Pareto前沿。根据ε的|M|个不同取值，首先对一组共计M=1,2,…,|M|个单目标M(ε)进行求解，并利用两阶迭代启发式算法(two-phase iterative heuristic, TIH)来求解第m个单目标问题M(εm)。

2.3 两阶迭代启发式算法

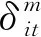
2.3.1 子问题LSP求解

求解LSP(εm,δm,λm)可确定工厂在哪个阶段生产和相应的生产量，以及每阶段给每个部队用户交付的器材量，但无法确定每个车辆具体的配送路径。在此基础上求解一系列VRP(εm)，可将求解LSP(εm,δm,λm)确定的每阶段给每个部队用户交付的器材量分配给每个车辆。

目标函数:

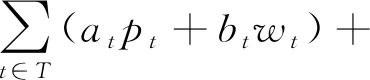
(28)

约束条件：(3)，(6)，(7)，(17)～(19)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

其中，目标函数(28)表示最小化生产，库存和近似访问总成本；式(29)表示订单精准执行率受εm约束；式(32)确保给所有部队用户的总交付量不超过所有车辆的总装载量与车辆载荷利用率的乘积；其它约束式与模型P中相应约束式含义相同。

2.3.2 子问题VRP求解

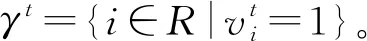
目标函数：

(36)

约束条件：

(37)

(38)

(39)

(40)

(41)

(42)

(43)

其中，目标函数(36)表示最小化配送路径总成本；式(37)～(41)为车辆路径约束。

本文之后调用Groör等[8]提出的VRPH算法对VRP(t,εm)进行求解，可确定每个车辆具体的配送路径Rkt，路径的数量NRt，和配送总成本RC。在所有VRP(t,εm)的解中，如果路径的数量NRt不超过物流服务商提供的车量总数|K|，LSP(εm,δm,λm)和VRP(εm)这两个子问题的解便可构成M(εm)的一个可行解。

2.3.3 参数更新机制

为寻得近似最优解，需要依次迭代地求解LSP(εm,δm,λm)和VRP(t,εm)这两个子问题，每次迭代过程中，算法会根据上一次迭代中VRP(t,εm)的解来更新参数集δm和λm。

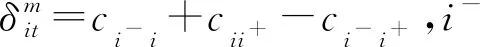
2.4 基于ε-约束的两阶迭代启发式算法

一般的ε-约束法只利用ε作为链接，而本文提出的ε-CTIH则通过ε、δ和λ这三个参数链接了M(εm)和M(εm+1)。

2.5 偏好解选择

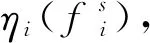
(44)

(45)

综上，利用ε-CTIH获取偏好解的主流程如图1所示。

图1 ε-CTIH获取偏好解的主流程图

3 实例计算与结果分析

3.1 实例背景

本文以某重型合成旅陆地阵地进攻战斗装备保障为背景，装备保障指挥部需协调某兵工厂临时应急生产单品种装备维修器材，并调用3辆相同类型车辆配送给阵地上的40个部队用户。决策者需要依据以往战斗装备损坏规律，为未来7天的战斗制定一个集成的器材供应保障计划，包括工厂每天生产多少，每天给每个部队用户交付多少，如何为给定的交付计划规划好配送路径，在降低总成本的前提下尽可能地最大化订单精准执行率。表1给出了该实例详细的参数设置。

表1 实例参数设置

本文首先设计了一个简单的三阶启发式算法来对总成本目标直接寻优。假设生产的器材只能存储在工厂，决策者首先根据各部队用户的需求确定每天的器材生产量以最小化生产成本，在此基础上求得一个最小化总库存成本的交付计划，最后根据确定的交付计划来生成车辆配送路径。本文之后调用CPLEX求解部分子问题，得到了一个总成本为439,630RMB，订单精准执行率为71.8%的方案。

3.2 结果对比分析

通过所提出的模型和ε-CTIH获得的Pareto解集如图2。图中，支配解已被剔除，纵坐标和横坐标分别表示订单精准执行率和总成本。求得Pareto解集后，可直接将所有解提供给决策者参考，也可以通过模糊逻辑决策法帮助决策者选择一个折中最优解。

图2 近似Pareto前沿

求解上述实例共获得29个Pareto解，从获得的Pareto前沿可以看出，两个优化目标之间存在一定的冲突。图中的两个实心正方形分别表示两个目标的近似下界和上界，实心三角形表示三阶启发式算法求得的解。显然，ε-CTIH求得的部分解占优于该三阶启发式算法求得的解。在订单精准执行率相同的情况下，ε-CTIH求得的解中成本降低了5.6%；在成本相同的情况下，ε-CTIH求得的解中订单精准执行率提高了近30%。

为帮助决策者根据偏好选择一个折中最优解，本文假设根据情况不同，决策者有3种不同的偏好：第一种情况下，决策者更注重总成本的控制，给第一个目标赋予的权重为ω1=0.7；第二种情况下，决策者同样重视两个目标，即ω1=0.5；第三种情况下，决策者更注重订单精准执行率，给总成本目标赋予的权重为ω1=0.3。图1显示了在上述3种不同的偏好下选择的解，从中可以看出不同的权重设置导致了不同的Pareto解。

表2 偏好解的详细信息

从表2可以看出，隶属度的取值范围从0.81到0.93，相对较高。如果决策者更注重成本的控制，选择的解中成本会增长6.28%，订单精准执行率提高37%；如果决策者更注重订单精准执行率，选择的解中成本会提高31.65%，订单精准执行率提高81%。从表中最后四列可以看出，订单精准执行率权重的增加会导致：(1)生产启动次数增多，生产成本增长；(2)给部队用户交付器材的频率更高，相应的运输成本也会增长；(3)每阶段结束时剩余的器材较少或无剩余，库存成本降低。

3.3 算法性能评估

在单目标优化中，可以利用下界或上界与获得的解进行比较来直接评价解的质量，而在双目标优化中，评价近似Pareto解集AF的质量相对较复杂，通常需要参考另一个Pareto解集，记为RF。为评估ε-CTIH的性能，本文基于ε-约束法框架，设计了一个新的运用CPLEX求解每个单目标问题M(εm)的算法，记为ε-CC。ε-CC的基本框架与算法2类似，但在调用CPLEX进行求解时，计算时间限制在14400s内，且M(εm)和M(εm+1)之间只通过参数ε来链接。本文中的AF和RF分别由ε-CTIH和ε-CC提供。

表3 参数生成规则

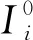
对比实验采用基数|Ar|、|RF|和计算时间T来评估算法性能，实验结果如表4。表中，第5至第8列统计了算法在5个实例上运行后各个评估指标的均值，TC和TH列分别表示ε-CC和ε-CTIH的平均求解时间，TLC和TLH列分别表示ε-CC和ε-CTIH求解5个相同规模实例所用的最长计算时间。

图3进一步给出了表中6个评估指标的详细对比结果。

表4 小规模实例对比实验结果

图3 ε-CTIH和ε-CC对比实验结果

比较表4和图3中的实验数据可以看出：

(1)从表4的基数列和图3(a)可以观察到，对包含10个部队用户和1辆车的实例，ε-CTIH与ε-CC生成的Pareto解的数量相差不大；在超过16个部队用户的实例上，ε-CTIH与ε-CC相比，能够提供更多的Pareto解；在规定的求解时间内，ε-CC无法为包含25个部队用户和2辆车的实例提供Pareto解。

(2)在求解时间方面，表4显示ε-CTIH和ε-CC求解的平均计算时间分别为159s和7546s，前者是后者2.1%，表明ε-CTIH的计算效率更高；从表4的最后一列可以看出，在所有实例上，ε-CTIH求解的最长计算时间的平均值比平均计算时间仅高出66s，表明ε-CTIH在求解时间上的稳定性较强；ε-CC求解的最长计算时间的平均值与平均计算时间之间有很大差异。此外，从图3(b)可以看出，随着问题规模的增大，ε-CC的求解时间呈指数级增长，增幅明显高于ε-CTIH。

4 结论

本文以经典的生产路径优化决策问题为基础，研究了装备维修器材PRP双目标优化决策问题。

(1)以总成本最小和订单精准执行率最大为优化目标，构建了一个双目标混合整数线性规划模型。

(2)针对模型非线性有约束的特点，开发了一个基于ε-约束法的两阶迭代启发式算法生成近似Pareto前沿，之后采用一种模糊逻辑决策方法帮助决策者根据偏好在诸多Pareto解中选择折中最优解。

(3)将提出的模型与算法应用于某次装备保障的实例，结果表明本文提出的模型真实有效，开发的算法和偏好解选择方法能够很好地帮助决策者做出器材供应保障决策。基于不同规模测试问题的数值实验表明，所设计的ε-CTIH求解双目标问题的效果好、计算效率高。