某条形承台的桩基受力探讨

麻洪辉 叶建龙 余茂峰

(浙江省交通规划设计研究院有限公司 杭州 310006)

桩基承台结构是桥梁中最常见的结构形式之一，上部荷载通过墩柱将力传至承台，再由承台将荷载传递给桩基，整个传力途径清晰可靠，在工程中已经得到广泛应用。桩顶力计算时一般都假定承台为刚体，根据现行《公路钢筋混凝土及预应力混凝土桥涵设计规范》(以下简称《公预规》)[1]第8.5.1条，单桩作用于承台底面的竖向力设计值计算方法见式(1)。

(1)

式中:Nid为第i根桩作用于承台底面的竖向力设计值；Fd为由承台底面以上的作用组合产生的竖向力设计值；Mxd、Myd为由承台底面以上的作用组合绕通过群桩形心的x轴、y轴的弯矩设计值；n为承台下面桩的总根数；xi、yi为第i排桩中心至y轴、x轴的距离。

由式(1)可知，不考虑弯矩影响，作用在桩顶的竖向轴力平均分配。而承台不是绝对刚体，它的变形仍受多种因素影响，承台下桩基内力也不是简单的均匀分配，按现行《公预规》计算的桩顶力与实际受力存在出入。

为研究某条形承台下桩基受力分配及影响因素，使桩基实际受力均匀，本文将建立承台受力模型，简化外部荷载，不考虑承台墩柱自重及承台底土面的支撑，利用有限元软件midas Civil分别模拟承台抗弯刚度、桩径及桩基间距等因素对桩基受力分配的影响，并对各影响因素进行规律分析，提出改进桩基不均匀受力的措施。

1 工程基本情况

某桥梁上跨地方国道，需在国道中央分隔带内设置桥墩。受空间等制约因素影响，墩柱采用独柱墩，墩底接条形承台，并在承台底布设3根桩基，桩基均为摩擦桩。

墩柱采用矩形截面，长、宽分别为2 m；承台长为B(m)、宽3 m、厚h(m)；桩基采用钻孔灌注桩，桩径为D(m)，桩间距为B1(m)；以上结构的材料均采用C30混凝土，弹性模量Ec=3×104MPa，结构简图见图1，有限元模型见图2。

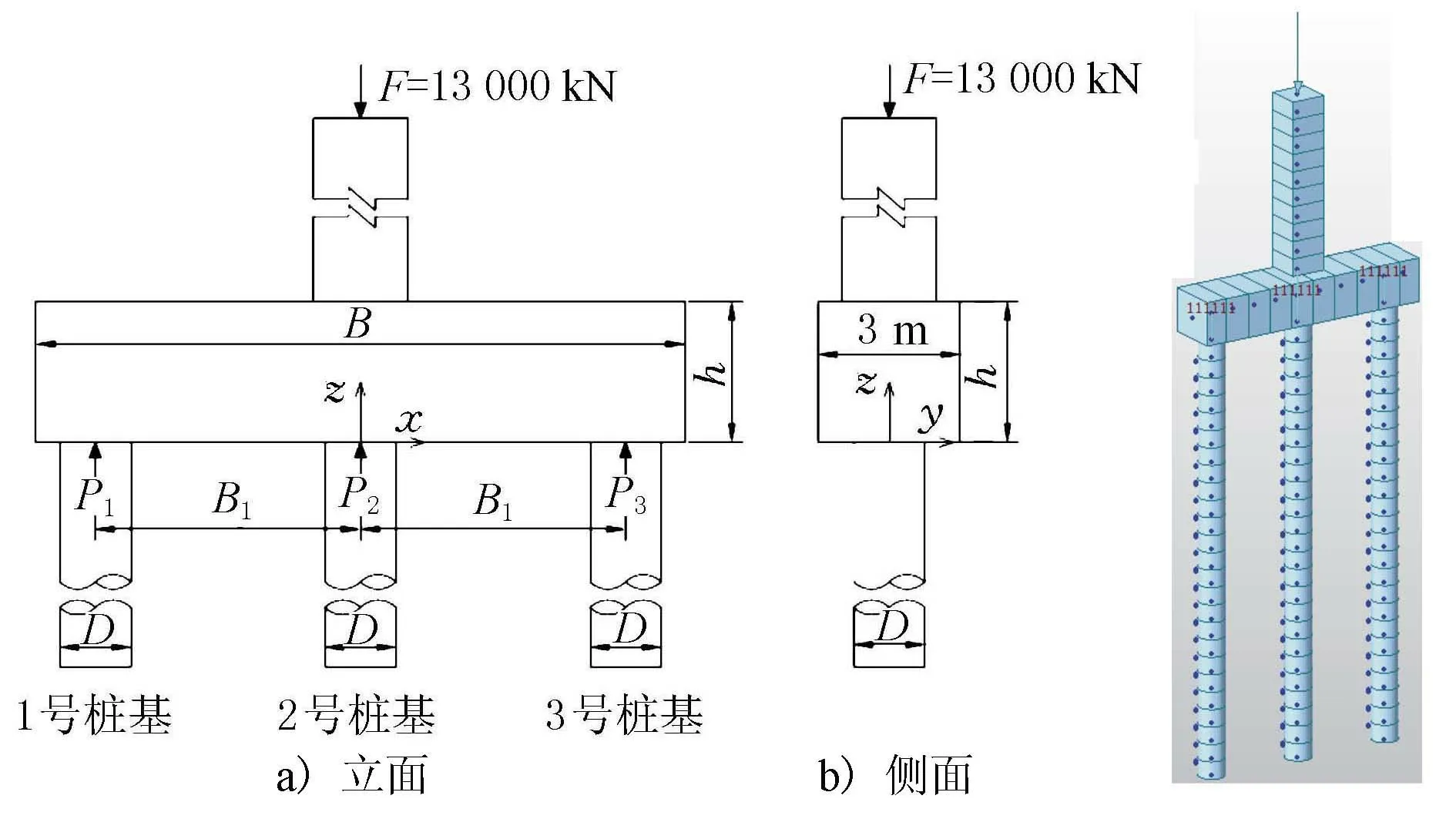
图1 独柱承台基础结构立面简图 图2 有限元模型侧面简图

本模型采用midas Civil 2019 V880软件计算，墩柱承台及桩基均采用梁单元，墩底与承台、承台与桩基采用刚性连接。在桩基各节点左侧建立塑性土弹簧单元，土弹簧上节点与桩基各节点分别刚接，下节点采用固定约束，根据实际地质层计算出各层土质的桩基侧摩阻力值和桩端承载力值，通过拟定塑性材料的弹性模量和初始单轴屈服应力建立土弹簧单元的竖向变形与侧摩阻力的相关性，同时，桩基各节点赋予水平方向弹性支撑，桩底节点另赋予竖直方向弹性支撑，各弹性支撑的刚度按m法算得，从而模拟桩基真实受力情况。以下分析均基于摩擦桩进行。

2 承台抗弯刚度对桩基受力的影响

承台的抗弯刚度直接影响承台的变形和桩基的不均匀沉降，从而影响桩顶的作用力[3-4]。现假定同一承台底下的地质土分层均匀，则各等径桩基承载力均一致[5-6]。

基于承台不同刚度对桩顶力的影响，拟定桩径D=1.5 m，B1=5.6 m，B=13.7 m，通过改变承台厚度h值，从而改变承台抗弯刚度EIy，建立方案A1～A5进行比较分析，具体方案见表1。

表1 不同承台抗弯刚度方案列表

为简化受力分析，在墩柱顶部仅施加F=13 000 kN竖直向下的集中荷载，并将承台顶部荷载按10级等分逐级加载，每级1 300 kN。得到不同外荷载下的桩顶力值，然后将该值与《公预规》桩顶力计算值Fd/3相比较，比较结果见图3、图4。

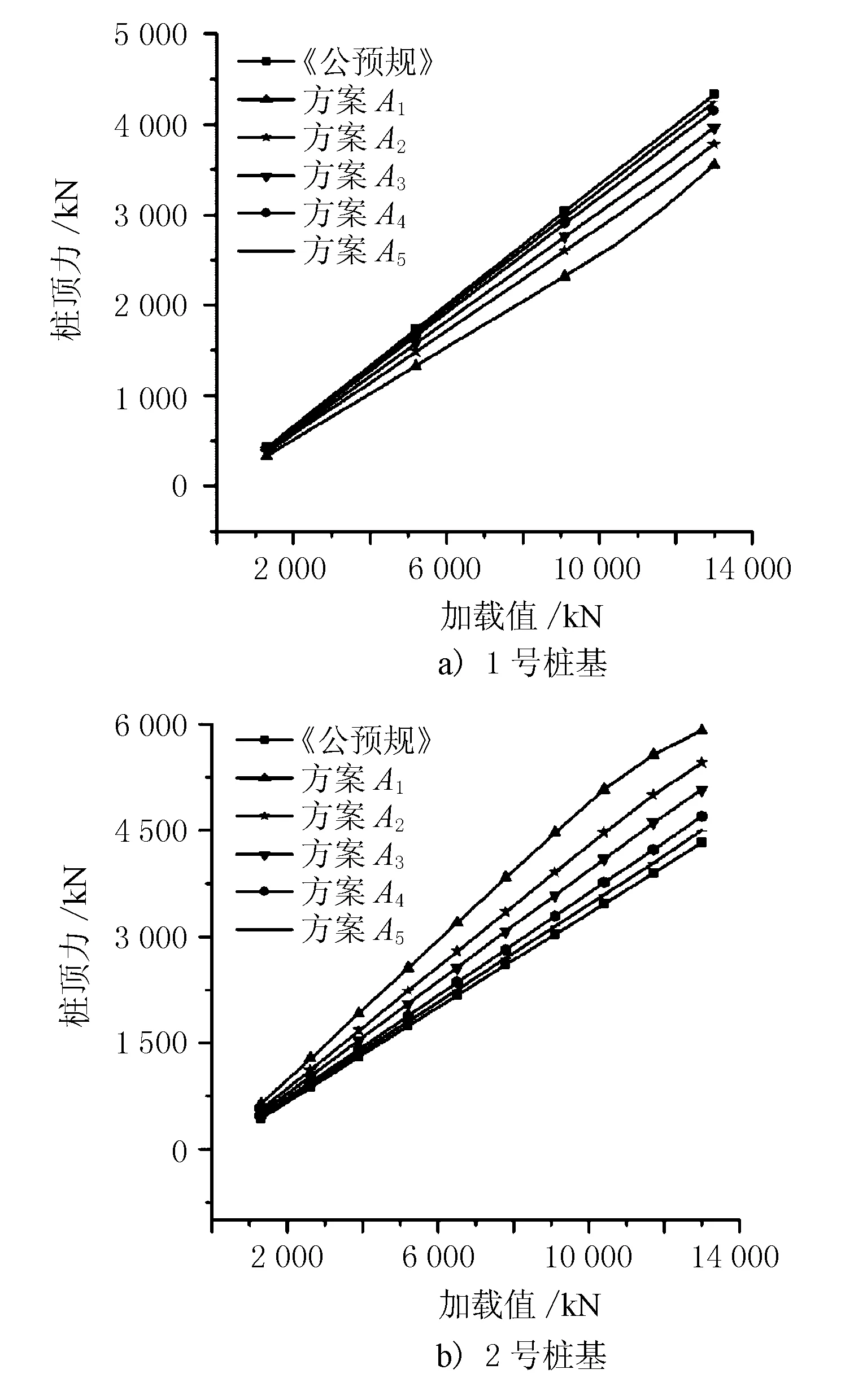
图3 不同方案下分级加载桩顶力

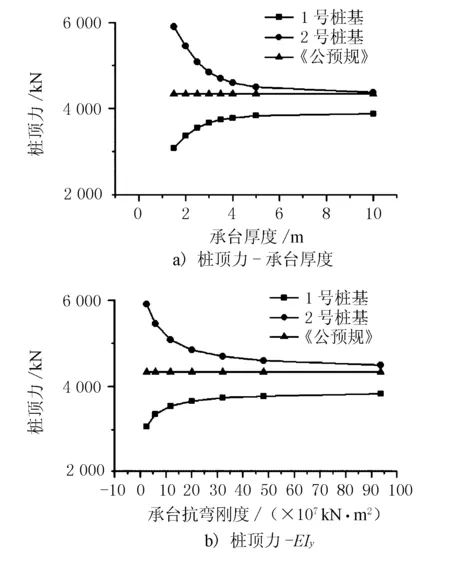
图4 桩顶力敏感性分析

由图3可知，①桩顶力和外荷载作用力基本呈现线性关系，随着承台抗弯刚度的增大，桩顶力值逐渐向《公预规》计算值靠拢；②当承台抗弯刚度比较小时(方案A1)，整个承台变形呈碟形分布，上部荷载主要由中桩(2号桩)承担，桩顶力为5 910 kN，占45.5%，边桩(1号桩)受力较小，桩顶力为3 545 kN，占27.3%，边中桩受力分布很不均匀。

由图4可知，承台厚度由1.5 m过渡到2.5 m时，边中桩的桩顶力变化剧烈，表明承台刚度由半刚性转化为刚性；而承台厚度由2.5 m过渡到4.0 m时，边中桩的桩顶力变化值已相对趋缓，表明承台刚性逐渐加强，此时承台的抗弯刚度为4.8×107kN·m2；承台厚度由4.0 m往更大厚度变化时，边中桩的桩顶力变化值很小，表明承台已趋于刚体。

图5为满载时边中桩受力漂移率图。

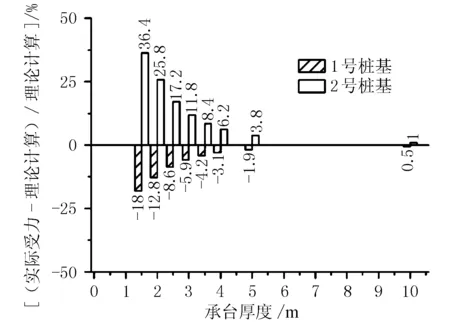
图5 边中桩受力漂移率(满载)

由图5可知，加至满载后，桩顶实际受力与理论计算值偏差值在25%以内时，承台厚度不应小于2 m；桩顶实际受力与理论计算值偏差值在20%以内时，承台厚度不应小于2.5 m；桩顶实际受力与理论计算值偏差值在10%以内时，承台厚度不应小于3.5 m。当承台厚度达到3.5 m后，继续提高承台厚度对承台底桩基受力分配影响较小。

综上所述，由于墩柱与中桩形心轴重合，在承台刚度有限的情况下，上部荷载由中桩承担的比例均高于边桩，中桩桩顶力均高于现行规范计算值；在承台达到一定刚度后，继续提高承台刚度对桩基受力分配影响很小。

3 桩径对桩基受力的影响

桩基顶部刚接承台，桩径的增加将增强桩基的承载力和抗压刚度，减小桩基沉降和自身变形，从而影响承台底部桩基的内力分配。

根据图1模型，拟定h=2.5 m，B1=5.6 m，B=13.7 m，修改桩径D为变量，建立方案B1～B4进行比较分析，具体方案见表2。

表2 不同桩径方案列表

加载方式同上，分10级加载，每级1 300 kN。计算不同加载值下的桩顶力值与规范计算值作比较，比较结果见图6、图7。

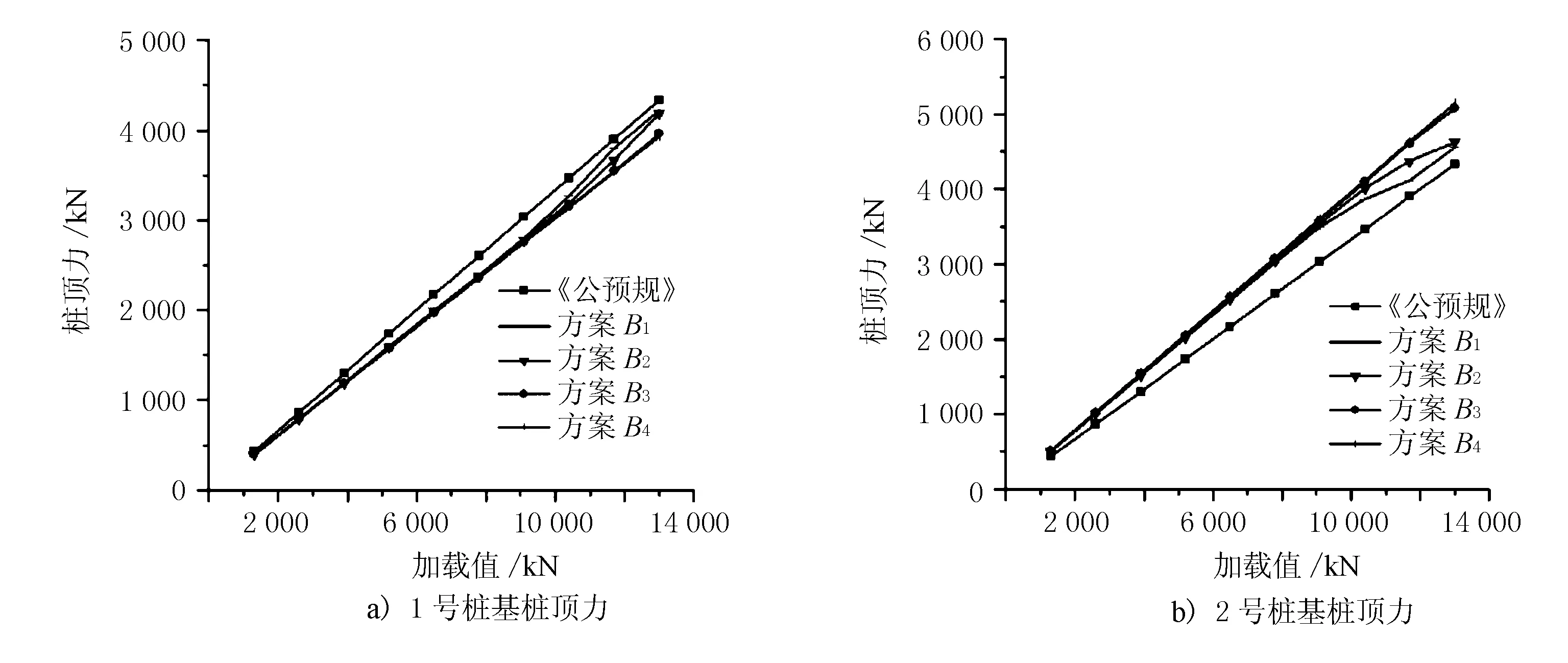
图6 1、2号桩基桩顶力(满载)

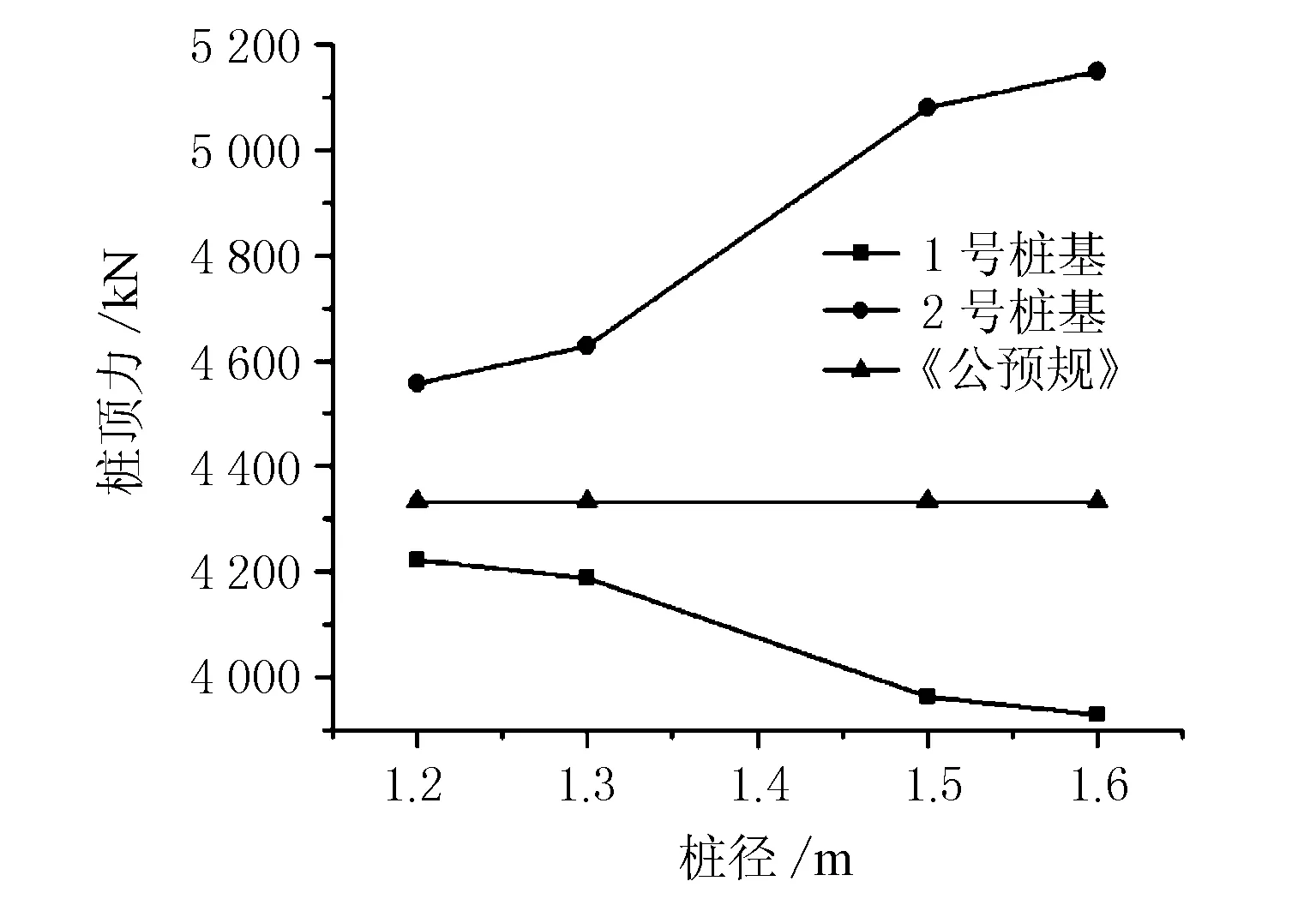
图7 桩径-桩顶力关系

由图6可知，①在桩基承载能力满足要求的情况下，加载值与桩顶力基本呈线性关系；②桩径较小时(方案B1和方案B2)，当外荷载加载至10 000 kN后，中桩(2号桩)的变形变大，边桩(1号桩)分担的承载力比例也明显增大；③中桩(2号桩)桩顶力大于现行规范计算值，最大增加了约18.8%，边桩(1号桩)桩顶力小于现行规范计算值。

由图7可知，加载至13 000 kN后，桩径从1.2 m增大至1.6 m时，中桩(2号桩)桩顶力由4 558 kN增大至5 149 kN，共增加了13%；边桩(1号桩)桩顶力由4 222 kN减小至3 929 kN，共减小了7%。

综上所述，在承台刚度一定的前提下，墩柱荷载将按照承台刚度进行内力分配传递至桩基。但由于墩柱与中桩形心轴的重合，中桩将先于边桩达到承载力极限值，并且随着桩径的增大，边中桩受力的不均匀性也将变大，建议边中桩可采用不同桩径设计以改进受力不均匀性。

4 桩基间距对桩基受力的影响

桩基间距直接影响承台在外荷载作用下的内力值和不同位置的竖向变形，从而影响桩顶力的分配。

根据《公路桥涵地基与基础设计规范》[2]第6.2.6条，钻孔桩中距不应小于桩径的2.5倍。在图1模型的基础上，承台厚度h取2.5 m，桩径D为1.5 m，修改桩间距B1为变量，建立方案C1～C5进行比较分析，具体方案见表3。

表3 不同桩基间距方案列表 m

加载方式同上，分10级加载，每级1 300 kN。计算不同加载值下的桩顶力值与规范计算值作比较，比较结果见图8、图9。

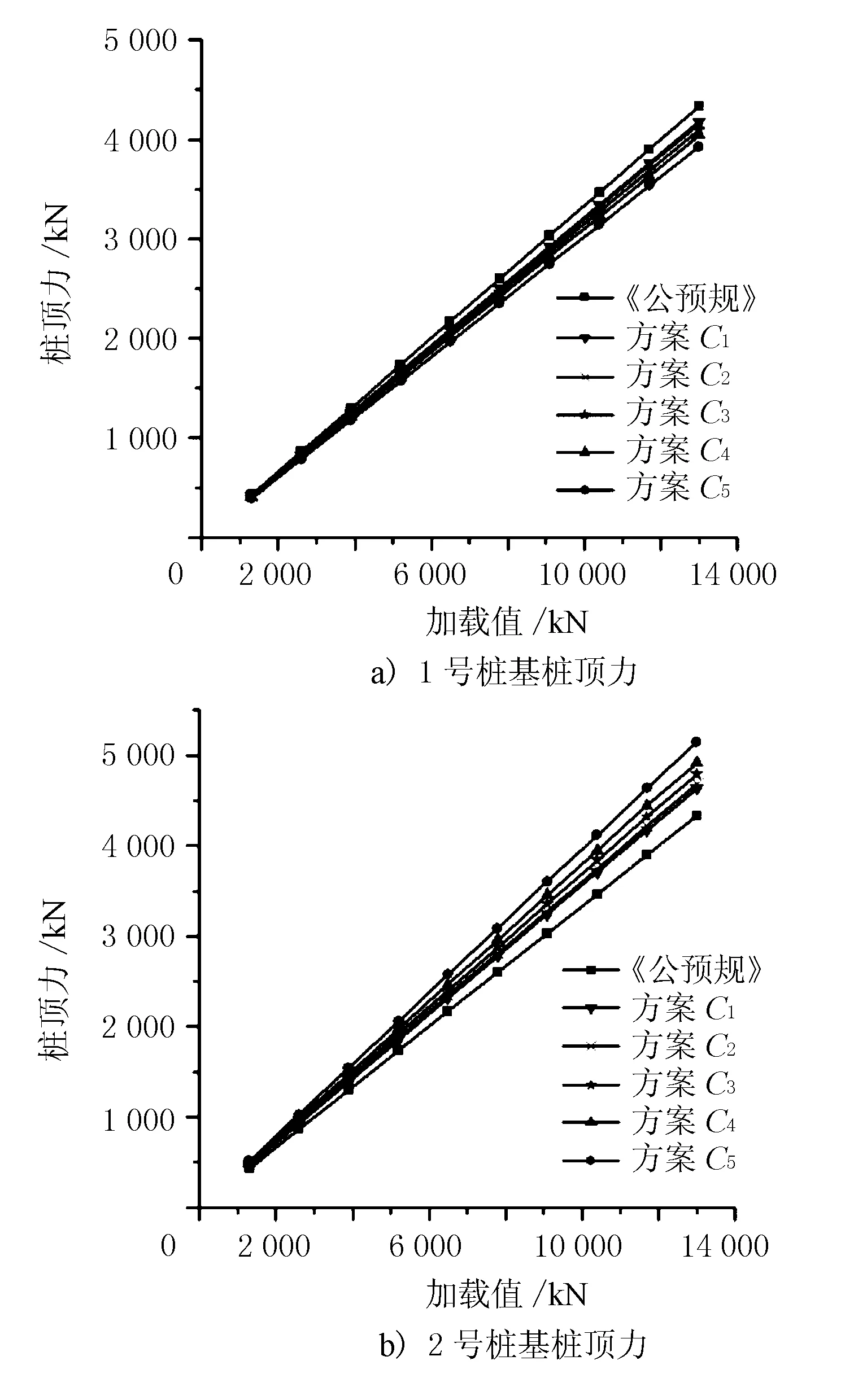
图8 1、2号桩基桩顶力(满载)

由图8可知，①在承台刚度一定时，加载值与桩顶力基本呈线性关系；②中桩(2号桩)桩顶力大于现行规范计算值，最大增加了约17.3%，边桩(1号桩)桩顶力小于现行规范计算值。

由图9可知，承台桩间距从3.75 m增大至5.6 m，中桩(2号桩)桩顶力由4 634 kN增加至5 149 kN，共增加了11%，边桩(1号桩)桩顶力由4 181 kN减小至3 929 kN，共减小了6%。

综上所述，在承台刚度一定的前提下，中桩桩顶力值将随着桩间距的增大而增大，边桩桩顶力值则随着桩间距的增大而减小。并且随着桩间距的增大，边中桩受力的不均匀性逐渐变大，建议尽量减小桩间距以改进边中桩受力不均匀性。

5 结论及建议

本文研究桩基承台在集中荷载作用下，通过分别改变承台抗弯刚度、桩径及桩基间距等因素，研究以上因素对桩基受力分配的影响规律，得出以下结论及建议。

1) 随着承台刚度的增大和桩间距的减小，桩基受力分配趋于均匀，但是承台刚度到达一定强度后，再增加承台刚度对桩基受力分配影响很小，建议根据工程实际合理采用承台的厚度。

2) 中桩桩顶力值将随着桩间距的增大而增大；并且随着桩径的增大，中桩桩顶力值还将继续增大。

3) 为准确计算桩基的内力分配，建议设计人员运用有限元软件对桥梁下部结构进行真实模拟，以提高设计的严谨性和准确性。

4) 改进桩基受力不均匀性的措施：边中桩可采用不同的桩径，同时应尽量减小桩基间距。