集中频段交通噪声垂直分布特性研究

乔 跃，袁嘉泽，张阳伟，卢振生，王迎辉，罗 毅

(绥化学院，黑龙江 绥化 152061)

0 引言

道路交通的发展和汽车数量的急剧增加导致了道路交通噪声污染日益严重，交通噪声成为四大污染物之一，是一个严重的社会公害问题[1]，严重影响了人们的生活和健康。所以为了更有效减少交通噪声的困扰，研究交通噪声的分布特性显得尤为重要。交通噪声纵向传播规律的研究是确定道路交通污染范围和污染区域界定的基础[2]。然而，迄今为止，关于交通噪声纵向传播规律的研究较少。交通噪声的垂直分布也严重影响城市居民生活状况，尤其城市对于声屏障的建立，需要以交通噪声垂直分布特性为参考依据进行设置[3]。本文以齐齐哈尔市内交通噪声污染严重路段两侧建筑物为研究对象，进行距地面垂直高度的交通噪声数据采集，依据声能量计算方法，找出此路段噪声能量占比严重的频段，再运用spss进行数据处理，找出交通噪声垂直分布特性。为高层的每层楼提出具体的防治措施；也可为声屏障的设置与设计提供参考，对于搞好噪声功能区规划、噪声污染防治及创造良好的城市环境具有重要意义。

1 实验数据采集与分析

1.1 试验条件

实验仪器：噪声频谱测量仪采用HS6288B型。定期进行了性能检验。

气象条件：风向保持不变，测量时风速不超过5 m/s。避免在湿的路面情况下进行测量。

测量时间：工作日车流量较大的高峰时段(07:30～8:30和16:30～18:30)

实验地点：采集纵向衰减规律所需要的数据时，所选择的测量地点是齐齐哈尔市车流量较大的新玛特附近卜奎大街两侧居民楼，全楼有十六层(每层楼的楼高3.3 m)。此楼符合纵向衰减研究的测量要求。

1.2 实验数据采集方法

数据采集方法：测量高层建筑交通噪声时，将HS6288B型频谱噪声仪放置在离任何反射物(即居民楼墙壁)2 m外，在早晚高峰进行测量，相隔10 min测量一次，每次测量15 min。测量时使用风罩。每次测量前后，都使用声校准器进行了校准。

2 交通噪声数据分析

由于不同道路车道宽度、车流量、行车速度以及汽车鸣笛情况的不同，其交通噪声的分布也不尽相同，为了探究某一特定道路交通噪声在垂直方向的分布特性，本文选取齐齐哈尔市车流量较大的卜奎大街新玛特附近两侧居民楼为研究对象。测量时，将靠近新玛特其中一侧的居民楼所有楼层窗户都打开，把仪器伸出窗外2 m，每层楼中各设多个测量点，一层接着一层的进行测量，每个测量点测量15 min，多次测量然后取平均值，之后统计15 min内交通噪声的等效声级(Leq(A))。测量标准按照GB/T14623—1993《城市区域环境噪声测量方法》的交通噪声测量办法。数据测量并整理结果见表1。

表1 新玛特附近居民楼高峰时段不同频率纵向交通噪声值

根据噪声频率调查结果，依据ISO226-1987噪声频段划分中的规定及声能量计算公式，求出各个频段的声能量分布，找到研究路段交通噪声最主要的影响频段，计算结果见表2。

表2 新玛特附近居民楼各层交通噪声声能量分布

声能量计算公式为

(1)

(2)

(3)

式中ηI——各频段声能量占总噪声能量的比值；

EI——各频段声能量/J；

EA——总声能量/J；

PI——各频段声压/Pa；

PA——总声压/Pa；

LI——各频段声压/Pa；

LA——总声压/Pa；

LIi——各频段各倍频程声压级/dB。

由表1和表2可知，新玛特附近居民楼各楼层噪声均为中频能量占比较大，随着楼层的增加中频占比更突显，说明随着楼层的增加，交通噪声主要影响频段在250～1 000 Hz范围内。低频能量分布在楼层低的时候占比和中频能量占比相接近，交通噪声高频段在每层的占比都较小，影响不显著。

研究城市道路交通噪声在空间的垂直分布，其主要目的是研究噪声对道路两旁高层住宅的影响。不同的楼层其噪声值不同，对居民生活的影响程度也是不一样的。交通噪声纵向传播规律的研究是确定道路交通污染范围和污染区域界定的基础。由上述分析得到新玛特附近居民楼受交通噪声中频段影响较大，所以找到在中频段(250 Hz、500 Hz、1 000 Hz)高度与交通噪声存在的对应关系，使城市降噪、创造良好居住环境更有针对性，能够可靠有效的降噪，减少其他次要因素干扰。

3 建立交通噪声垂直分布关系模型

由表1可知，频率在250 Hz、500 Hz、1 000 Hz时，在中间楼层出现了噪音最高点，噪声分布与高度的关系总体趋势大致相同，都呈现先增加后降低的趋势。所以可以选择主要影响特定路段的频段(250 Hz、500 Hz、1 000 Hz)对应的数据来推测出交通噪声与高度是否存在数学关系。交通噪声值的衰减状态与垂直高度的关系可通过以下方法求得：将数据导入SPSS数据分析软件中，选中可能形成的曲线模型(线性、二次、三次、指数方程)，最后得到拟合结果。

由图1和表3可知，线性曲线及指数的显著值都大于等于0.8，说明两个模型均不显著，拟合效果差，线性曲线与指数曲线均不适合来描述样本。二次曲线模型与三次曲线模型统计量的显著值都等于0.000，远远小于0.01，说明两个模型都显著，并且都具备常数项,分别为：64.133和61.917。二次曲线模型的拟合度”低于“三次曲线模型拟合度”(0.801<0.811)，所以交通噪声垂直分布特性更符合一元三次曲线模型。根据表3曲线估计结果，得到三次曲线方程为：噪声值=0.008×楼层数3-0.43楼层数2+1.789楼层数+61.917。

表3 模型汇总和参数估计值(因变量:频率250)

图1 250 Hz时曲线估计拟合图

由图2和表4可知，线性曲线及指数的显著值分别为0.136和0.128，远大于0.01，说明两个模型均不显著，拟合效果差。二次曲线模型与三次曲线模型统计量的显著值都等于0.000，远远小于0.01，说明两个模型都显著，并且都具备常数项,分别为：73.366和74.866。二次曲线模型的拟合度低于“三次曲线模型拟合度”(0.952<0.960)，所以交通噪声垂直分布特性更符合三次函数方程。根据表4曲线估计结果，则三次函数曲线方程为：噪声值=-0.005×楼层数3-0.006楼层数2+0.633楼层数+74.866。

表4 模型汇总和参数估计值(因变量:频率500)

图2 500 Hz时曲线估计拟合图

由图3和表5可知，线性曲线及指数的显著值分别为0.728和0.763，远大于0.01，说明线性曲线与指数曲线均不适合来描述样本。二次曲线模型显著值为0.002>0.01也不显著，拟合效果差，三次曲线模型统计量的显著值等于0.000，远远小于0.01，说明显著，具备常数项：72.604。三次曲线模型拟合度为0.866，所以交通噪声垂直分布特性更符合一元三次曲线方程。根据图3曲线估计结果，三次曲线方程为：噪声值=-0.02×楼层数3+0.43楼层数2-0.493楼层数+72.604。

表5 模型汇总和参数估计值(因变量:频率1 000)

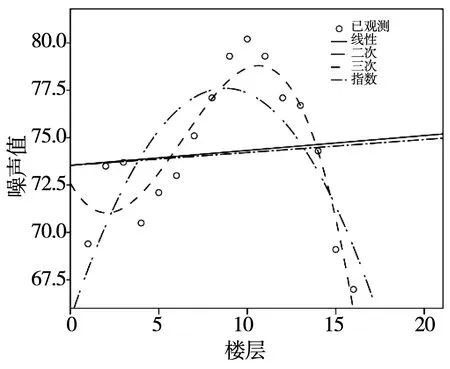
图3 1 000 Hz时曲线估计拟合图

4 结论

本文选取交通噪声污染严重的路段(齐齐哈尔市新玛特附近居民楼)为研究对象，采集了距地面不同垂直高度所对应的噪声数据，进行整理分析后得到：

(1)所测路段(齐齐哈尔市新玛特附近居民楼)交通噪声主要来源为中频段噪声。

(2)频率在250 Hz时，垂直高度与对应噪声值的关系：噪声值=0.008×楼层数3-0.43楼层数2+1.789楼层数+61.917。

(3)频率在500 Hz时，垂直高度与对应噪声值的关系：噪声值=-0.005×楼层数3-0.006楼层数2+0.633楼层数+74.866。

(4)频率在1 000 Hz时，垂直高度与对应噪声值的关系：噪声值=-0.02×楼层数3+0.43楼层数2-0.493楼层数+72.604。噪声值与垂直距离之间呈三次曲线模型分布。

掌握交通噪声垂直方向上的分布规律可以来防治道路交通噪声对高楼居民生活的影响，针对高层楼的每层楼提出具体的防治措施；尤其对于需要设置声屏障的路段，可作为声屏障的设置与设计参考依据，对于搞好噪声功能区规划、噪声污染防治及创造良好的城市环境具有重要意义，为营造城市良好的声环境提供理论支撑。