平行板电容器极板间电场及电容的计算探讨*

孙云娟

(河南师范大学新联学院，河南 新乡 453007)

0 引言

1 一个“无限大”均匀带电平面激发的电场

设平面上的电荷面密度为σ，由于电荷在平面上的分布是均匀的，因此在平面两侧的电场具有平面球对称性，与平面等距离的各点，其电场强度的大小相等，方向与平面垂直。过场点P和平面左侧对称的点P′，作一个圆柱形的高斯面，其轴线与平面垂直，两底面与平面平行，面积为ΔS，如图1、图2所示[1]。

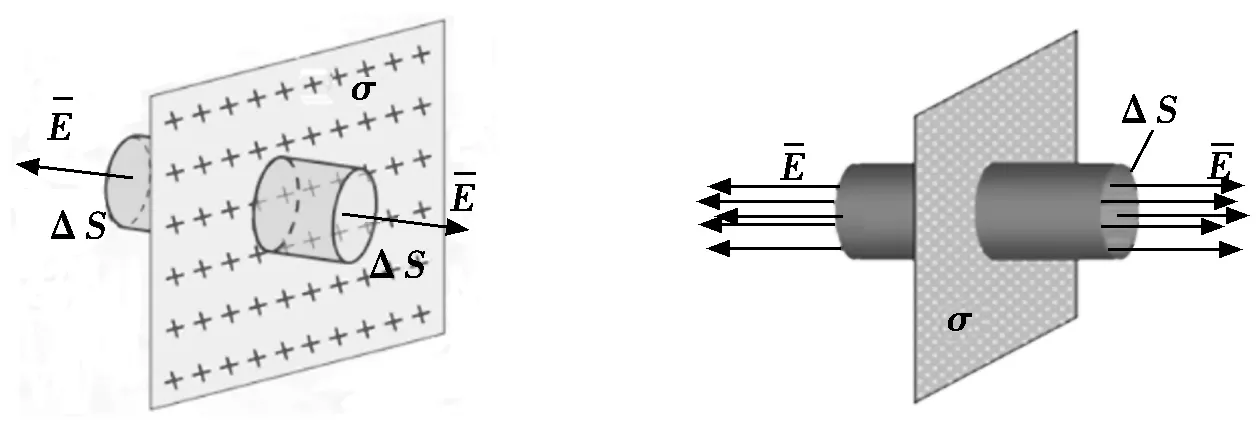
图1 “无限大”均匀带电平面的电场 图2 “无限大”均匀带电平面电场线与高斯面的关系

根据高斯定理：

设通过图1、图2中圆柱形高斯面的电场强度通量为ΨE，即:

考虑到挤压制粒过程中，当模孔入口处的挤压力被撤去时物料仍紧紧束缚在模孔中不会脱落，说明物料与模孔内壁在下一次挤压开始之前就存在预应力PN0，则计算PN时应考虑预应力PN0对制粒挤出过程的影响，因此PN应改写为如下形式：

2 平行板极板间的电场强度

利用上题结论，证明一对电荷面密度均为σ，等值异号的“无限大”均匀带电平行平面间电场强度的大小[2]。

图3平行板电容器极板间的 图4A点的电场强度方向

匀强电场

3 平行板极板间的电容C的推导计算

根据平行板电容器的电容公式：

(1)

Q=σS.

(2)

(3)

将式(2)和式(3)带入式(1)，得到：

(4)

式中常量ε0称为真空电容率(permittivity)，或真空介电常量(die-electric constant of vacuum)，是电磁学的一个基本常量，2010年国际推荐值为

(5)

将式(5)带入式(4)，可得：

(6)

式中k为静电力常量，k=8.9875×109N·m2/C2

如果平行板电容器极板间充满电容率为ε的电介质[4]，则

(7)

4 结语