基于双向长短期记忆神经网络的风电预测方法

刘永强，续 毅，贺永辉，柳文斌

（1.国网吕梁供电公司，山西 吕梁032200；2.山西合邦电力科技有限公司，山西 太原030006）

随着能源短缺和环境问题的日益突出，开发可再生能源成为应对该问的重要举措[1-3].可再生能源如风电、光伏发电等在近年来得到快速发展，截止到2018年底，全球可再生能源总发电量（不包括水电）为2 480.4 TWh，比2017年增长14.5%，其中风力发电和光伏发电分别为1 270 TWh和584.6 TWh[4].中国的可再生能源总发电量（不包括水电）为640.7 TWh，其中风力发电和光伏发电分别为367.7 TWh和180.2 TWh，可再生能源在未来一段时间内还将继续增长[4].

越来越多的可再生能源接入电网，对电网带来了新的挑战[5-6].本文针对风力发电展开相关研究，风电是一种具有间歇性和波动性的可再生能源，这种特性对其并网、调度等带来一定不利影响.风力发电的预测技术成为缓解这种影响的一种有效方式，它可以根据风力发电的预测数据进行日前或实时的调度，或利用储能系统平抑其波动性[7-9].

针对风电的预测方法，国内外已有诸多研究.差分滑动平均自回归模型（Autoregressive Integrated Moving Average model，ARIMA）是一种常见的时间序列预测模型[10，11]，文献[12]提出了一种基于ARIMA模型的风电预测方法，对模型的窗口长度等进行了系统选择.相对于ARIMA模型，神经网络（Neural Networks，NN）模型在拟合变量之间的非线性关系方面具有优势，它是由输入层、隐含层和输出层组成的网络，每个神经细胞间的信息通过加权后传递给下一层，并进行相关计算[13].通过对给定的输入与输出相对应数据的进行训练学习，可以得到细胞间的权重值，进而拟合输入与输出之间的关系.文献[14]提出了一种改进神经网络的风电预测方法，提高了收敛速度和预测精度.

针对NN模型在预测时无法计及较早之前的信息，循环神经网络（Recurrent Neural Network，RNN）应运而生，它的特别之处在于在细胞上加入了循环结构，通过该结构来记忆较早之前的信息[15].长短期记忆（Long Short-Term Memory，LSTM）神经网络是一种特殊的RNN，它将RNN的细胞结构进行了改进，避免出现梯度消失或梯度膨胀的问题[16-17].文献[18]提出了一种考虑空间相关性采用LSTM的预测方法，考虑了将具有空间相关性的光伏与目标电站的预测结合，提高了光伏预测的准确性.文献[19]提出了将小波分解与LSTM相结合的方法，在对风电进行分解的基础上，利用LSTM分别对各个分量进行预测建模.

以上的结构均基于利用过去信息预测当前值，双向长短期记忆（Bidirectional LSTM，BiLSTM）神经网络对LSTM进行了改进，增加了反向隐含层，既可以在前向隐含层利用过去数据，又可以在反向隐含层利用未来数据，这样得到的预测结果更加准确[20].文献[21]提出了利用双向LSTM对蛋白质残基相互作用进行预测的方法，将预测精度提高10%以上.

本文基于BiLSTM对风力发电进行预测，首先介绍了LSTM和BiLSTM的基本原理，其次介绍了利用BiLSTM进行风电预测的基本框架结构，及预测的评价指标.最后在MATLAB中编写仿真程序，并与多种预测方法进行了对比，用实际算例表明了仿真结果的正确性.

1 神经网络模型

1.1 单向LSTM神经网络

在传统的神经网络中，预测所使用的历史数据是预测时刻前n个时刻的信息，每次预测所用的历史信息是向前滚动的，但是在预测时这种方法会造成对较早以前的信息忽略的情况.RNN的设计则可以避免这一问题，它将隐含层的输出值返回输入当中，成为一个循环的单元，这种学习训练过程可以将较早的信息作为预测参考因素.RNN的典型单元如图1所示，左侧为其在神经网络中的表示方法，右侧为其在时间轴上的展开形式，可见，在t时刻的输入细胞的信息中包含了t-1时刻的输出值，并依次进行下去.

图1 RNN的循环结构Fig.1 The loop structure of RNN

RNN在每一个时刻的训练都计及了过去所有时刻的部分信息，并将该时刻的信息传递下去.但是，RNN的神经单元只包含一个函数，如图2（a）所示，每经过一个时刻，就要在原来函数的基础上叠加函数，多次叠加则会造成梯度消失或者梯度膨胀问题，即损失了较早之前的信息或者之前的信息占比非常大.

LSTM是一种特殊的RNN，由于独特的设计结构，LSTM适合于处理和预测时间序列中间隔和延迟非常长的重要事件.LSTM通过设计来避免长期依赖问题.如前所述，所有RNN都具有一种重复神经网络模块的链式的形式，在标准的RNN中，这个重复的模块只有一个非常简单的结构，例如一个tanh层.不同于单一单元结构，LSTM的单元结构有四个组成部分，四个部分之间存在交互，分别是遗忘门、输入门、信息更新和输出门，如图2（b）所示.

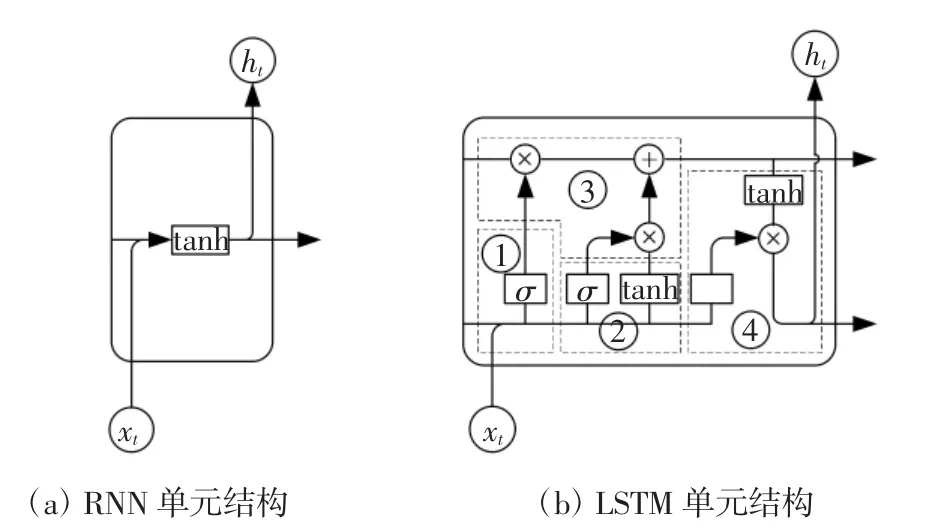
图2 两种类型的神经单元对比Fig.2 Comparison of two types of neural units

LSTM的第一个组成部分为遗忘门，图2（b）中①所示，即通过sigmoid函数从上一个时刻的输出和本时刻的输入值中丢弃部分信息，其表达式为：

第二个组成部分为输入门，图2（b）中②所示，该部门的功能是确定需要更新哪些信息，输入门的输出值分别通过sigmoid和tanh函数进行选择过滤，需要更新的信息的表达式如下.

经过σ函数：

经过tanh函数：

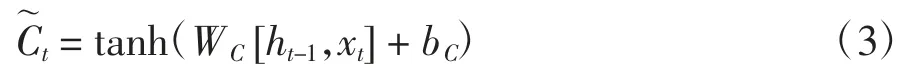
第三部分为信息更新，图2（b）中③所示，它将遗忘门和上一时刻的信息更新值相乘并与输出门的两个值的乘积相加，细胞状态的更新公式为：

第四个组成部分为输出门，这个输出值基于以上三个步骤.首先，由sigmoid函数选择输入门的部分信息；其次，利用tanh函数将更新后的信息进行选择过滤；最后，将两个选择后的信息相乘得到该时刻的细胞输出值，其表达式如下.

经过σ函数：

以上各公式中，xt为时刻t的输入值，ht-1为t-1时刻的输出值，Ct为细胞状态更新值，W[·]为权重值，b[·]为偏置值.

本文选取神经网络中常用的sigmoid函数作为σ函数，tanh函数也为神经网络中的常用函数，其表达式分别如（7）和（8）所示.

1.2 双向LSTM神经网络

单向LSTM具有处理和预测时间序列中间隔和延迟非常长的重要事件的特点，但是它只能考虑过去数据的信息来进行预测，如用过去几个时刻的天气预报预测数据，预测可再生能源发电的功率.这将导致只利用的距离预测时刻最近的若干个历史数据，忽略了较早的历史数据包含的信息.双向LSTM具有利用过去和未来数据的信息进行学习的能力，即可以利用过去和未来的天气预报预测数据来推导可再生能源发电功率.双向LSTM的示意图如图3所示，从下向上依次为输入层、前向层（Forward）、后向层（Backword）和输出层.双向LSTM的基本思想是每一个训练的序列向前和向后分别是两个长短期记忆神经网络，而且这两个层都连接着输入层和输出层.输出值综合了过去（前向）和未来（反向）的信息，在风电功率预测中，则是过去和未来的风速预测数据，根据风速的预测信息进而实现对风电功率的预测.

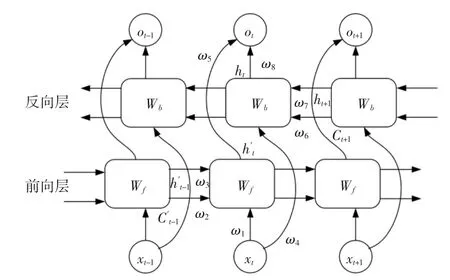
图3 BiLSTM示意图Fig.3 Schematic diagram of BiLSTM

双向LSTM的每一个时刻都有8个独特的权重值被重复利用，8个权重值分别对应：输入到前向和后向隐含层的权重值（w1，w4），前向隐含层到前向隐含层（w2，w3），后向隐含层到后向隐含层（w6，w7），前向和后向隐含层到输出层（w5，w8）.需要注意的是，前向隐含层和后向隐含层之间没有信息传递，这样可以避免两个隐含层的相邻两个时刻之间形成死循环.其计算方式为：在前向层从1时刻到t时刻正向计算一遍，得到并保存每个时刻向前隐含层的输出；在后向层沿着时刻t到时刻1反向计算一遍，得到并保存每个时刻向后隐含层的输出.最后在每个时刻结合前向层和后向层的相应时刻输出的结果得到最终的输出，数学表达式如下

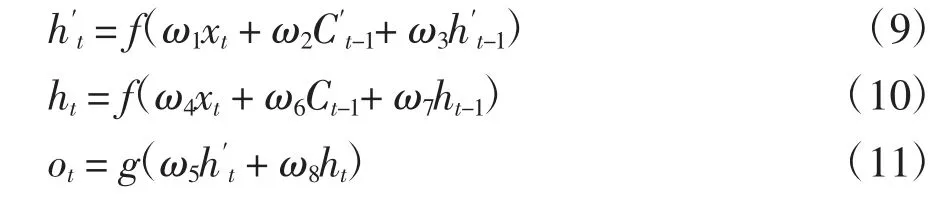
2 风电预测模型及评价指标

2.1 双向LSTM神经网络风电预测模型

利用神经网络模型进行预测，通常利用历史数据训练神经网络，建立输入与输出的关系，训练完成后，利用现有输入数据预测未来的数据.本文通过对历史数值天气预报（NWP）风速数据与风电功率的历史SCADA数据进行分析，使风电的功率与NWP风速数据建立联系.由于利用过去的风速数据信息预测风电功率具有一定的局限性，因此，双向LSTM利用过去的风速数据信息和未来的风速数据信息进行预测得到的风电功率会更加准确.

基于双向LSTM的新能源日前预测方法的框图如图4所示，首先对历史NWP风速预测数据和历史SCADA风电功率数据进行处理，提取对应的值；其次，建立双向LSTM预测模型，将对应数据输入预测模型进行训练；再利用评价指标对预测模型进行评价并选择最佳模型；最后，将日前NWP的风速预测数据输入训练好的LSTM神经网络，得到风电功率的日前预测值.

在预测模型中，用于训练的数据为一年的风速和风电数据，训练时输入层为历史NWP风速预测数据，输入层的个数为2 m+1个，输出层为历史SCADA风电功率数据，个数为1个，即历史NWP风速数据：St-m，St-2，St-1，St，St+1，St+2，St+m，其单位为m/s；历史SCADA风电功率数据：St，其单位为kW.由于过去和未来的风速数据与此时刻的风电功率之间的关系不同，输入层的数量需要通过敏感度分析确定，神经网络训练的目的是学习输入变量和输出变量之间的关系，因此通过对输入层个数敏感度的分析，并以预测精度为指标对输入层个数进行评价，进而选择最佳的输入层个数.

2.2 评价指标

不同预测模型的新能源预测结果是不同的，如BP神经网络、LSTM神经网络、双向LSTM神经网络等，此外，输入层个数也会影响预测精度.本小节总结了以下几种常用的指标对预测结果进行评价，并在仿真结果中对三种指标的适用性进行分析.

图4 BiLSTM风电预测框图Fig.4 Wind power forecast block diagram of BiLSTM

1）均方根误差评价指标，指标越小，预测误差越小.

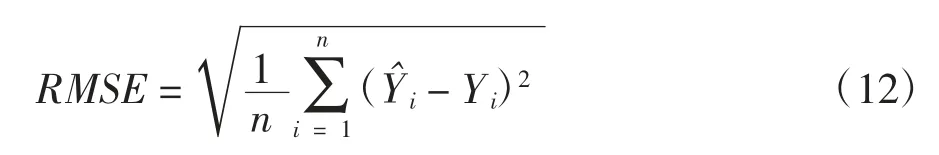
2）对称均值绝对值百分比误差，该指标的值越小表示预测误差越小.

3）希尔不等系数，它介于0-1之间，数值越小表示预测误差越小.

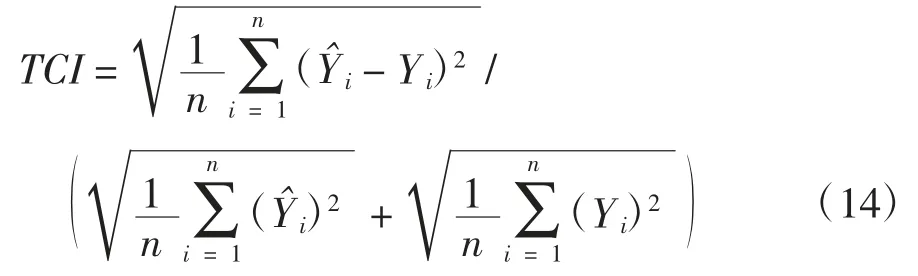
3 算例分析

本文采用某风电场一年的数据对所提出的方法进行仿真验证，采样时间为15 min.本节截取了一段时间的数据，如图5所示，为标幺化后的风速和风电功率曲线，风速和风电功率具有很强的相关性.本节将对BILSTM模型所采用预测数据个数的敏感度进行分析，并对不同方法下的风电预测结果进行对比，根据评价指标选择最佳模型.

图5 风速与风电功率曲线Fig.5 Wind speed and wind power curve

隐含层的神经单元的个数不仅会影响神经网络的学习效果，还会影响训练时间，因此，首先需要确定隐含层神经单元的个数.本文以RMSE为指标对不同神经单元个数进行了仿真分析，如图6所示，由于以1个单元为间隔的RMSE值和仿真时间相差不明显，本文以5为单位进行仿真.随着神经单元数量的增加，训练时间的增长趋势加快，但学习精度减小的趋势变慢，因此，本文中选取隐含层神经单元的个数为35.

图6 隐含层神经单元个数与时间、RMSE关系Fig.6 The relationship between the number of neural units in the hidden layer and time and RMSE

如2.1节中所述，用于预测风电功率的风速预测值数据个数2 m+1是不确定的，需要以2.2节中的评价指标对预测数据个数进行敏感度分析.如图7所示，本文对不同指标下的风速预测值个数的敏感度进行了对比分析.纵轴为指标的大小，横轴为2m+1中的m.由图可见，指标RMSE与TIC、SMAPE相比，当m变化时，RMSE没有反复的上下波动，有先减小后增加的趋势；TIC次之，但其波动幅度不大，也有先减小后增加的趋势；SMAPE的趋势最不明显，出现多次波动，相对难以确定最佳的m.可间三种评价指标中，RMSE的评价效果最理想，更适用于本文对风电预测结果的评价.RMSE和TIC的最小值均出现在m=19的时候，而SMAPE在m=19出的值也相对较低，因此，在本文的算例中，当m=19时，基于BiLSTM的风电功率预测效果最好.

图7 不同m下的指标对比Fig.7 Index comparison under different m

如图8所示，为BiLSTM的学习过程，横轴为迭代次数，纵轴为指标RMSE.由图可见，可以将学习过程分为三个阶段，125次之前，随着迭代次数增加，RMSE迅速减小并带有较大的波动性；253次之前，出现了明显的趋势变化，波动幅度减小，趋势更加平滑，但RMSE仍有较大的减小；253代之后，变化趋势减缓，RMSE的变化很小.整个训练过程的迭代时间为123 s.如图9所示，为m=19时，BiLSTM的风电功率预测值与实际值的曲线，两者相差较小，均方根误差RMSE为0.069.

表1为不同风电预测方法的指标对比，对于传统神经网络，其预测效果是最差的，与LSTM和BiLSTM相比，RMSE和TIC指标均大一倍以上，SMAPE相差较小.LSTM次之，BiLSTM的效果最好.以RMSE、TIC和SMAPE指标衡量，BiLSTM效果相对于LSTM分别提高了10.25%、6.71%和12.18%.

图8 BiLSTM的学习迭代过程Fig.8 Iterative learning process of BiLSTM

图9 风电实际值与预测值曲线Fig.9 Curve of actual and forecast wind power values

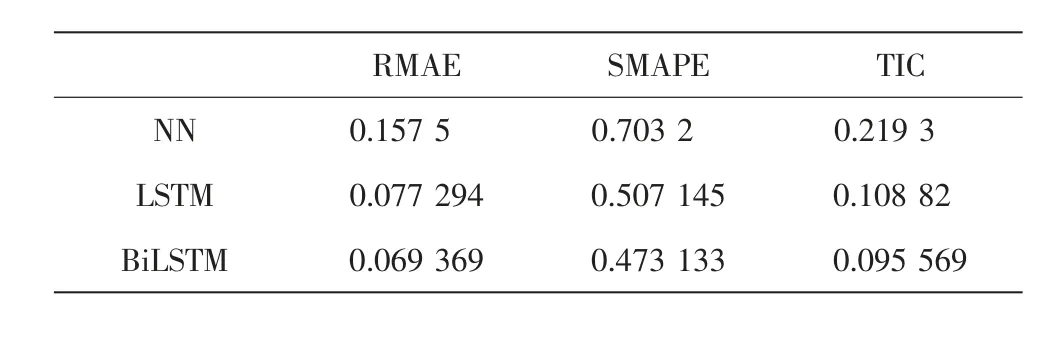
表1 不同方法的指标对比Tab.1 Comparison of indicators of different methods

4 结论

本文提出了利用BiLSTM进行风电功率预测的方法，介绍了LSTM和BiLSTM的数学模型，建立了利用风速预测数据进行风电功率预测的模型及其评价指标.以实际的风电数据对所提方法进行了仿真验证，得到了BiLSTM隐含层的最佳神经单元个数；计算了不同风速个数对预测结果的影响并得到最佳风速个数；对比了不同预测方法的预测效果，BiLSTM效果相对于LSTM分别提高了10.25%、6.71%和12.18%.该方法为风电的预测打下了理论基础，对风电场的调度、平滑功率波动等实际应用提供了一定的依据.