复合Mlinex损失下艾拉姆咖分布参数的Bayes估计

张 晗, 周菊玲, 董翠玲

(新疆师范大学 数学科学学院, 新疆 乌鲁木齐 830017)

0 引言

艾拉姆咖分布是武器装备维修理论中的常用分布.张月等利用概率密度函数的变窗核估计方法,讨论了艾拉姆咖分布参数θ的经验Bayes检验问题[1].王敏在复合Linex对称损失下对不同先验分布的艾拉姆咖分布参数进行了估计[2].吕佳等讨论了当参数的先验分布为Gamma分布时,在复合Linex对称损失下,艾拉姆咖分布的参数估计并证明其容许性[3].龙兵在定数截尾数据下给出了不同先验分布的艾拉姆咖分布参数的Bayes点估计和区间估计,还讨论了在全样本场合不同损失函数对参数估计的影响[4-5].季海波分别在平方损失、二次损失、Linex损失、熵损失、对称熵损失和平衡损失函数下研究了k阶Erlang分布参数的Bayes估计问题[6].复合Mlinex损失是金秀岩在Mlinex损失函数的基础上定义的一种对称损失函数[7].本文基于复合Mlinex对称损失函数,得到了艾拉姆咖分布在先验分布为共轭先验、无信息先验以及Jeffreys先验下的Bayes估计,并通过随机模拟对估计进行了比较.

单参数艾拉姆咖分布的概率密度函数和分布函数分别为

(1)

其中x>0,且θ>0是参数

金秀岩提出的复合Mlinex对称损失函数[7]形式为

(2)

其中δ为θ的估计.

设X1,X2,…,Xn为来自艾拉姆咖分布总体的一个随机样本,则X=(X1,X2,…，Xn)的联合概率密度为

(3)

1 参数θ的Bayes估计

引理1[8]在复合Mlinex对称损失函数和模型下,对任一先验分布π(θ),θ具有唯一的Bayes估计:δ=[E(θc|X)/E(θ-c|X)]1/2c,且估计是容许的.

1.1 共轭先验下的参数估计

定理1 设随机变量X服从艾拉姆咖分布,当参数θ的先验分布服从逆伽玛分布IG(a,b)时,在损失函数式(2)下,θ具有唯一的Bayes估计

(4)

证明已知参数θ的先验分布服从逆伽玛分布IG(a,b),其密度函数为

(5)

根据Bayes公式,由式(3)、(5)可得θ的后验概率密度函数:

(6)

即θ的后验概率密度函数服从逆伽玛分布IG(2n+a,b+2t).

又因为

(7)

同理

(8)

所以,根据式(7)、(8)可得θ的唯一Bayes估计

(9)

定理得证.

1.2 无信息先验下的参数估计

定理2 设随机变量X服从艾拉姆咖分布(1),当参数θ的先验分布服从无信息先验时,在损失函数式(2)下，θ具有唯一的Bayes估计

(10)

证明参数θ的无信息先验分布为

π2(θ)=1

(11)

由式(3)、(11)可得θ的后验密度为

(12)

因此在复合Mlinex损失函数下,θ的Bayes估计为

(13)

定理得证.

1.3 Jeffreys先验信息下的参数估计

定理3 随机变量服从艾拉姆咖分布(1),当参数θ的先验分布服从Jeffreys先验时,在损失函数式(2)下，θ具有唯一的Bayes估计

(14)

证明取参数θ的先验分布为Jeffreys先验

(15)

由式(3)、(15)可得θ的后验密度为

(16)

则在复合Mlinex损失下有

(17)

定理得证.

2 数值模拟与实证分析

2.1 数值模拟

利用MATLAB进行数值模拟,通过Monte-Carlo法产生一组容量n=30的艾拉姆咖分布随机样本,根据不同的先验分布由定理1、定理2、定理3计算出参数θ的Bayes估计值.

1) 在复合Mlinex对称损失下,当参数θ的先验分布为逆伽玛分布时,Bayes估计值如表1和表2.

表1 n=30,θ=1,t=30.1400,a=1时δB的结果

表2 n=30,θ=1,t=30.1400,b=1时δB时的结果

观察表1和表2中的数据,可以看出在复合Mlinex对称损失下,当参数θ的先验分布为共轭先验IG(a,b)时,超参数a,b的取值对参数θ的估计没有明显的影响.

2) 在复合Mlinex对称损失下,当θ的先验分布为无信息先验和Jeffreys先验时,参数的Bayes估计值如表3.

表3 n=30,θ=1,t=30.1400时δN、δJ的结果

根据表1、2、3中的极差R，可以看出在复合Mlinex对称损失下,三种先验分布下参数θ的Bayes估计值的精确度和稳健性没有明显的差别；并且c的θ变化对的影响也不明显.

3) 三种先验分布下参数θ的Bayes估计值,如表4所示.

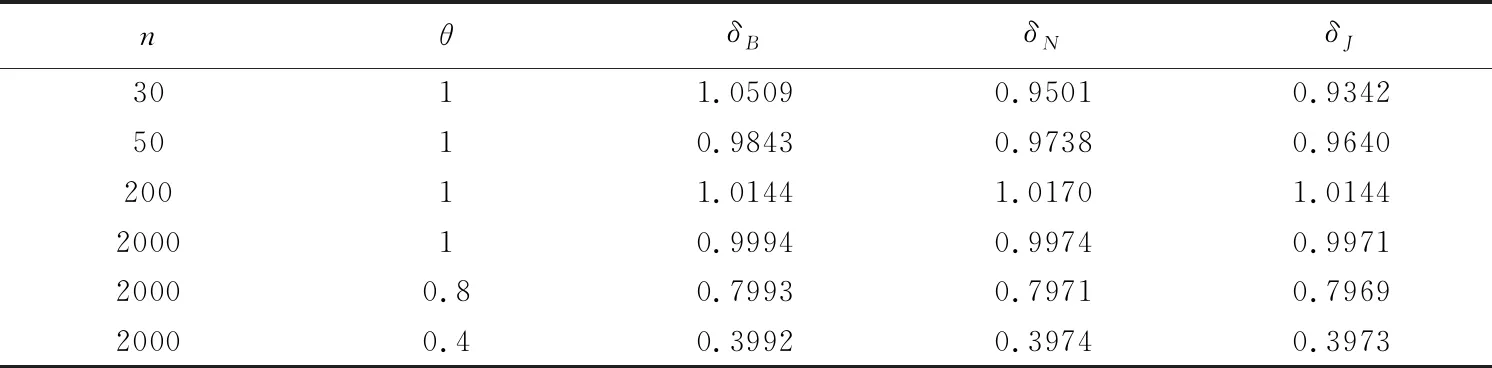
表4 参数θ的Bayes估计

从表4中可以看出,对于θ的不同取值,三种先验分布下的估计都是一样稳健的.通过比较,在复合Mlinex对称损失函数下,当参数的先验分布为共轭先验时,计算所得的Bayes估计比其他先验分布下的估计更加精确并且样本容量越大，估计越接近真值.

为了进一步表明艾拉姆咖分布在复合Mlinex对称损失函数下的Bayes估计值更加精确,与其他损失函数进行对比.下面直接给出两个结论:在先验分布为共轭先验时，艾拉姆咖分布参数的Bayes估计在二次损失函数和熵损失函数下的表达式为

比较结果如表5所示.

表5 n=30,θ=1,t=30.1400时复合Mlinex对称损失、二次损失和熵损失下的Bayes估计

表5说明了先验分布为共轭先验时，通过选择合适的逆伽玛分布参数和c的值,艾拉姆咖分布参数在复合Mlinex对称损失函数下的Bayes估计比在二次损失函数和熵损失函数下更接近真值.

2.2 实证分析

例1[9]在某型坦克维修过程中,经过47次观察得到基层I级预防性维修二级保养时间的观测值，如表6所示.

表6 预防性维修二级保养时的实验统计观测值

通过文[9]可知, 上述观测值近似地服从参数θ=5.46的艾拉姆咖分布.对该数据进行统计分析, 见表7.

表7 复合Mlinex对称损失、二次损失和熵损失函数下的参数估计

观察表7可知,在同一损失函数下,参数θ的先验分布为共轭先验时,Bayes估计更稳健.同时数据也表明艾拉姆咖分布参数在复合Mlinex对称损失函数下的Bayes估计比在二次损失函数和熵损失函数下更精确.

3 总结

本文主要研究了当艾拉姆咖分布参数θ的先验分布为共轭先验、无信息先验和Jeffreys先验时,在复合Mlinex对称损失函数下的Bayes估计.数值模拟的结果表明,损失函数中的参数c不影响θ的估计值；当先验分布为共轭先验时,Bayes估计值最接近艾拉姆咖分布的真值.和二次损失和熵损失进行了简单对比,结果表明艾拉姆咖分布参数θ在复合Mlinex对称损失下的Bayes估计更精确.最后通过实证分析证明了模拟的结果.