生态系统害虫防治的一种脉冲控制数学模型的全局稳定性

左冰冰， 金浩城， 郭俊荣

(浙江农林大学 理学院，浙江 杭州 311300)

引 言

我国作为一个农业大国，在农业生产过程中生物灾害频频发生，害虫对农作物的危害不可忽视[1]。为了保证农作物的产量和质量，农业上尽可能使用各种措施防治害虫[2]。

目前，相对于其他防治措施，化学防治高效、速效、使用方便、适应性广、经济效益显著，然而化学防治仍存在着很多不足[3-5]。化学防治常用的防治手段是喷洒农药，而农药中的有效成分在消灭害虫的同时，也会对自然天敌产生毒害作用，严重时可能会导致敏感型生物的种群衰落和灭亡，破坏农田的生态平衡和物种多样性[6]。

生物防治是目前有害生物治理中较为成功、节约和对环境安全的方法[7]。在早期的生物防治中，最好的方法是利用自然天敌来防治对植物造成毁灭伤害的昆虫[8]。但这一类天敌一般只有成虫期可以捕食害虫[9]。生物防治的缺点在于没有化学防治效果明显，见效慢，需要一定的反应周期，且防治植物病虫害的种类不多，受到环境等诸多条件的限制，需要与其他防治方法结合进行[10]。

鉴于上述讨论，本文开发的脉冲控制数学模型，用瞬时脉冲模拟对生态系统无害的天敌和化学杀虫剂，从数学角度分析害虫防治。通过模拟结合生防与化防为一体的害虫综合治理措施，可以既安全又有效地将害虫虫口密度控制在防治指标以下。

1 脉冲控制数学模型的建立

种群动力学属于生物数学学科，是一种研究种群宏观现象的科学，研究种群和环境两者之间的关系，研究不同种群之间的关系。研究不同种群之间的关系时，我们时常能从动力学的角度加以分析，进而建立数学模型，以此类推，生态学现象也可以用模型来研究，以期达成控制某些生态问题的目标[11]。

在本模型中讨论的相互作用类型为害虫幼虫为害，且仅有成熟天敌可取食害虫幼成虫。

图1中直线代表取食关系，虚线代表害虫形态转化。

图1 模型中种群关系模式图

在本模型中植物与有害生物种群之间的相互作用通过Holling Type-2来表示，因为它包含了有害生物处理食物和搜寻猎物所需的时间。这些时间与Holling Type-l相区别并可以得到更好的结果。除了用公式表达数学模型，还研究了系统有界性，害虫灭绝平衡点的局部稳定性，解释分析系统的全局吸引性，系统的持久性。

(1)植物种群x(t)以r为增长率呈指数增长，且环境承载量为k，α为食饵所承受的捕食压力，b1为害虫繁殖率，即幼虫虫口密度y1(t)取食植物种群x(t)的虫均取食率用αx(t)y1(t)来表示。

(2)y2(t)是在时间t时该区域的有害生物成虫虫口密度，假定只有成熟的天敌才能捕食害虫种群，γ是捕杀率常数。此外，d2是害虫种群的自然死亡率。

(3)未成熟天敌群体z1(t)的增长率取决于成熟天敌z2(t)。天敌的死亡率和成熟率分别为d3和m1，ε是天敌的捕食转化率。

(4)成熟天敌群体z2(t)因未成年天敌群体z1(t)的增长而增长。此外，d3是成熟敌人的死亡率，T为添加杀虫剂脉冲的周期。

据此，我们建立以下模型：

(1)

2 预备知识和引理

以下内容,将给出一些对后续证明非常有用的符号、定义以及引理。

定义2.1当脉冲微分方程

(2)

Δx=x(t+)-x(t)=Bkx(t),t=τk,k∈Z

满足以下条件时：

(H1)A(t)∈PC(R,Cn*n)且A(t+T)=A(t)(t∈R)，

(H2)Bk∈Cn*n,det(E+Bk)≠0,τk<τk+1(k∈Z),

(H3)存在q∈N，使得Bk+q=Bk,tk+q=tk+T(k∈Z)，

那么我们称系统(1)是线性的T-周期脉冲微分方程。

设φ(t)是系统(2)的基解矩阵，且存在唯一的非奇异矩阵

M∈Cn*n，

使得

Φ(t+T)=Φ(t)M

(3)

定义2.2我们把方程(3)中的常数矩阵M称为相应于基解矩阵φ(t)的单值矩阵。

注：系统(2)的所有单值矩阵都相似，从而有相同的特征值。

定义2.3称脉冲系统(2)的单值矩阵的特征值M1,M2,…Mn为其Floquet乘子。

引理2.1(Floquet乘子理论)，设条件(H1)…(H3)成立，则线性T-周期脉冲系统(2)是：

(1)稳定的，当且仅当它的所有乘子μj(j=1,…,n)的模小于1或等于1，即|μj|≤1，而且模等于1的乘子μj有相应的单重初等因子；

(2)渐近稳定的，当且仅当它的所有乘子μj(j=1,…,n)的模小于1，|μj|<1；

(3)不稳定的，如果存在某个乘子μj，使得|μj|>1。

定义2.4设，如果：

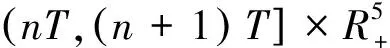
(2)V关于x是局部Lipschitzian的，那么称V是属于V0类的。

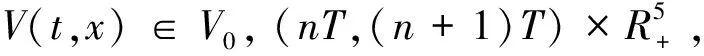
引理2.2设x(t)是系统(1)的解，并且满足初值条件x(0+)≥0，那么对所有的t≥0均有x(t)≥0。若x(0+)>0，则当t>0时，有x(t)>0。

我们将用到下面比较重要的引理。

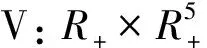
假设

D+V(t,x)≤g(t,V(t,x)),t≠nT

V(t,x(t+))≤ψn(v(t,x)),t=nT

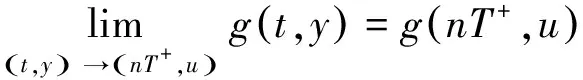
设r(t)是下列方程：

u′(t)=g(t,u),t≠nT

u(t+)=ψn(u(t)),t=nT

u(0+)=u0

在[0,∞)上的最大解。那么由V(0+,x0)≤u0就可得到：

V(t,x(t))≤r(t),t≥0，

其中x(t)是系统(1)的任意解。

引理2.4对下面的脉冲微分方程：

我们有此方程的正周期解：

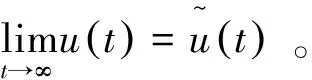
证明：

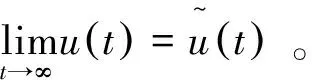
由于

故当t→时，即证毕。

现在我们回到系统(1)，当害虫灭绝时(即y1(t)=y2(t)=0)我们有以下脉冲微分方程：

(4)

(5)

对方程(4)使用引理1，可得，

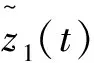
(6)

g(t)=z2(t)exp(d3(t-nT)),t∈(nT,(n+1)T]

由于

另一方面，

所以，我们结合上式可得

因为

z2((n+1)T+)=z2((n+1)t)+μ2，

容易发现有唯一的正不动点

因此，我们有

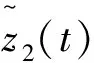
3 主要结果

定理3.1对任一系统(1)的解：x(t),y1(t),y2(t),z1(t),z2(t)。

存在一个常数M>0，使得对充分大的t，有：

x(t)≤M,y1(t)≤M,y2(t)≤M,z1(t)≤M,z2(t)≤M

证明：

将系统(1)带入上述值可得：

由于

考虑

u(t+)=u(t),t=nT，

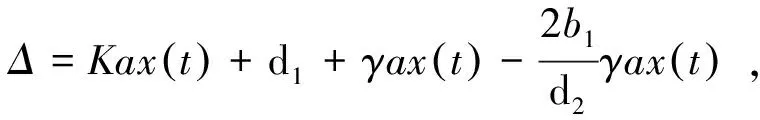
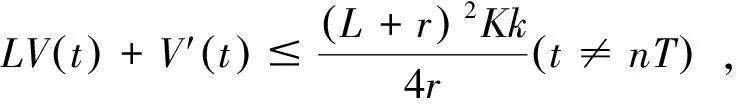
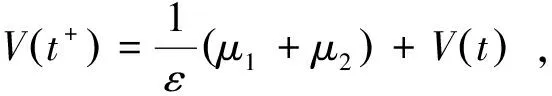
当t→∞时，故V(t)是一致有界的。V(t)≤M′，当t充分大时，

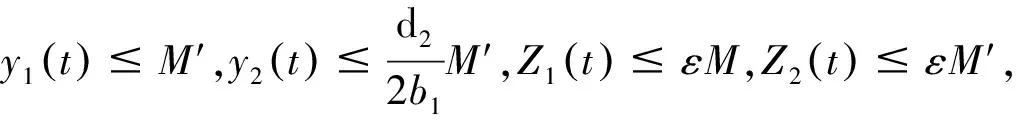
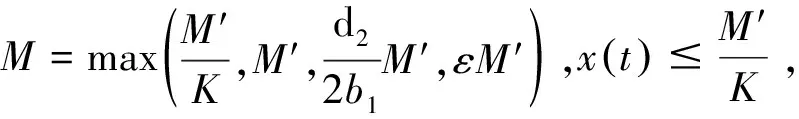
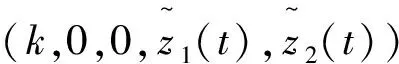
证明：

x(t)=k+Φ1(t),y1(t)=Φ2(t),y2(t)=Φ3(t),

其中：φi(t),i=1,2,3,4,5为相应的小振幅扰动，系统(1)可以扩展为如下的线性形式：

令φ1(t)=(φ1(t),φ2(t),φ3(t),φ4(t),φ5(t))则上述线性形式可记为：

设φ(t)为此系统的基解矩阵，φ(t)满足

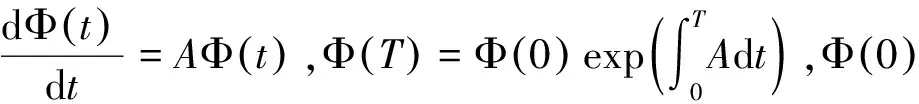
λ1=exp(-rT)<1,

λ2=exp(-d3T)<1,

λ3=exp(-(d3+m1)T)<1,

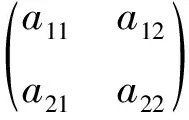
a21=e-d2T;

证明：

由于(x(t),y1(t),y2(t),z1(t),z2(t))为系统(1)的任意解

考虑如下比较系统：

对于u(t)具有不稳定解u(t)=0和稳定解u(t)=k。由比较原理可得x(t)≤u(t)，故对任意小的正值ε1，存在N1>0，对于所有t>N1，有x(t)≤k+ε1。

对于z1(t)，有：

考虑如下比较系统：

由引理1，我们可以得到正周期解

且此周期解具有全局渐近稳定性。

对于z2(t)同样有如下系统：

由

利用引理1，可得

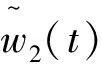
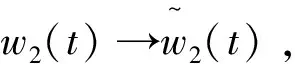
对于y1(t)与y2(t)，

(1)如果b1-d2≤0，必有y1(t)+y2(t)趋于0；

(2)如果b1-d2>0则有：

=(b1-d2+βM)(y1(t)+y2(t))-(b1-d2+d1+βM)y1(t)

由于y1(t),y2(t)非负，故有y1(t)趋于0；当t趋于∞时，y2(t)趋于0。当t趋于∞时，下面讨论x(t)：

由于前面对t>N1，有x(t)≤k+ε1，且存在

∃N4>0，∀t>N4有x(t)≥s(t)>k-ε1，

这就证明了当t趋于∞时，x(t)→k。

当t→∞时，已得

因为y1(t)→0，故

∃N5>0，∀t>N5,

z1(t+)=z1(t)+μ1,t=nT,

将z1(t)与下面的系统比较，

由引理1，

z2(t+)=z2(t)+μ2,t=nT

4 结果讨论

本文基于固定时刻，利用脉冲微分方程建立相应的数学模型，周期释放天敌并喷洒农药来进行害虫治理，我们可以得出以下结论：在生物防治和化学防治结合的综合治理下，如果添加脉冲的周期T小于阈值Tmax，那么系统存在一个全局渐近稳定的害虫灭绝周期解。这也符合实际的生物学现象，通过本文所建立的模型，我们提出了新的问题，例如：如何优化表示天敌释放量的参数？如何把握季节性虫害的防治时期？如何将害虫与天敌的取食习性更加细化？如何将不可控制的气候因素用参数表示？如何得到害虫控制阈值？如何证明当T大于阈值Tmax时系统处于动态平衡？如何证明系统存在周期解、拟周期解及混沌？基于上述问题，我们今后将继续研究。