基于模糊综合评价方法的中性点接地方式选择方法及算例分析

赵帅　徐祥征　胡文广　王利娜

摘 要：随着配电网电缆线路的使用比例逐渐增加，为了保证电网供电的可靠性，选择了最佳的中性点接地方法.根据南昌市供配电线路统计，不同中性点接地方式失效时系统参数的特点，建立了包含故障电流、弧光接地过电压和发生故障时的线路跳闸率在内的安全性能评价指标.建立Fuzzy-AHP模型，得到三个主要安全绩效指标的隶属函数，利用层次分析法得到的相应权重，进行模糊综合评价，进行最优中性点接地方式选择，经过算例验证了该方法的实用性和一定的工程参考价值.

关键词：中性点接地;弧光接地;线路跳闸率;隶属函数

中图分类号：O159;TP301.6  文献标识码：A  文章编号：1673-260X（2020）03-0008-04

低压配电网的中性点接地方法是集继电保护，绝缘水平和系统运行的综合问题[1]，世界各地由于网络结构差异、电压等级不同、用电端要求等原因，一直存在着中性点接地方式选择的分歧，也缺少综合性考虑且可行性较好的选择方法[2].目前，中国低压配电网的中性点接地方式有中性点不接地，小电阻接地，通过高阻接地，通过灭弧线圈接地等几种方式，但都存在一些优缺点[3-4].本文根据201X年南昌市供配电线路故障统计情况，进行简要事故分析.并在变电站故障数据的基础上，综合分析了故障电流、弧光接地过电压倍数、故障跳闸情况及系统规划等因素，根据层次分析法总结其影响，利用模糊评价法对其进行分析，并根据综合评分得出给定条件下中性点接地方式的最优选择.该选择法综合考虑了中性点接地方式与各大故障因素之间的关系，综合电网要求，对中低压配电网中性点选择有着一定参考作用.

1 南昌市配电线路故障统计分析

根据南昌市201X年配电网络变电站数据统计分析，故障电流、接地过电压及跳闸情况具体数据在此隐去，部分故障统计情况如表1.

由数据可知南昌配电线路跳闸857条次，重合闸成功468条次，重合闸不成功389条次，重合闸成功率为54.61%;接地229条次，应急抢修342条次;因故障停电960条次，因用户申请8条次，重合闸成功率为54.61%.变电站合计10kV线路跳闸超过10次的变电站有11个，变电站合计10kV线路跳闸超过5次的变电站有24个.线路跳闸超过3次及以上的线路有33条，其中跳闸超过5次的线路有15条，变电站10kV线路接地超过10次的变电站有9个，变电站接地超过5次的变电站有20个，频繁接地线路超过5次及以上的线路有7条线路，接地超过3次及以上的线路有24条.

由此故障统计也可以看出，随着南昌市区电力电缆应用的增多，消弧线圈的弊端也渐渐暴露，电容电流已达到了相当高的级别，主要体现在[5-6]：（1）消弧线圈补偿残流大，容易发生弧光接地过电压.（2）消弧线圈无法有效补偿高频电流.（3）消弧线圈的容量受到限制.因此很多实际工程开始研制开关型消弧装置.面对增加城市电缆比例的趋势，变电站中性点接地方式的选择对整个配电网的可靠性有着非常重要的影响.因此，需要一种更合理的中性点接地方法选择方法，为提高电网的安全运行能力提供参考.

2 基于模糊评价-层次分析法的中性点接地选择

2.1 安全性评价指标建立

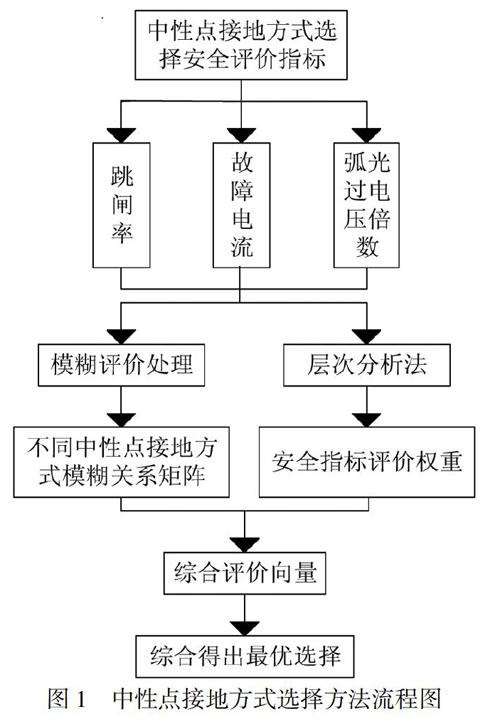
根据对中性点接地方式影响因素程度的分析，选取了故障电流、弧光接地过电压倍数及故障跳闸情况等作为此次数学模型分析的重点.其选择流程结构如图1所示.

2.1 Fuzzy-AHP模型

Fuzzy-AHP模型是基于层次分析法（Analytic Hierarchy Process）得出权重的模糊综合评价方法，这种该综合法根据模糊数学的隶属度理论将定性评价转化为定量评价.由于中性点接地方式的具体适用性难以量化，属于典型的模糊非线性问题[8]，因此采用了Fuzzy-AHP模型对其进行处理.可以根据其清晰明确的结果进行系统地评价.

模糊评价方法需要根据评价量化体系，将评价分为：满意度高、满意度较高、满意度一般、满意度较低、满意度低五个等级.具体如表2所示：

根据评估，构建并量化分层隶属函数，并进行进一步的模糊评估处理.由于X1故障跳闸率、X2故障相接地电流/A、X3弧光接地过电压倍数都属于越小越良好型，于是有隶属度函数：

对与某中性点接地选择时，其测定量为U=（？覬1，？覬2，？覬3），其对应的评价指标的模糊关系矩阵为：

通过引进层次分析法对各安全影响指标进行权重分级，将其重要性进行量化，从而得到判断矩阵.其判断标准如表3所示：

根据此评价指标重要性量化分级准则，可以得到相应的判定矩阵A.通过计算一致性比例CR，来判断矩阵一致性是否可接受[9].

经推导计算，得到各安全评价指标的权重向量Q=（q1，q2，q3），其中q1计算公式为：

则根据式（7）、式（8），可得综合安全指标评价向量为：

3 实例验证

本文选取南昌市某变电站10kV段，其线路参数如表4所示，利用ATP-EMTP进行仿真计算得到不同中性点接地方式，发生单相接地故障的故障电流与过电压倍数，和相关统计的故障跳闸率，如表3-2所示，其中新型接地方式为仿真数据，所有电缆线路路为YJV22-240/10kV，架空线型号为JKLYJ-120/10kV其跳闸率按45%计算.

根据式（1）至式（5）所得的隶属函数，得到相应的模糊关系矩阵：

计算得到一致性比率为0.0068，满足一致性要求.随后，根据式（8），求得权重向量为：Q=（0.52 0.27 0.14），最终得到综合评价向量为：

P小电阻=（0.03 0.27 0.43 0.69 0.61）

P消弧線圈=（0.11 0.7 0.82 0.3 0.13）

P不接地=（0.1 0.27 0.92 0.75 0）

P新型=（0.03 0.27 0.43 0.57 0.73）

判定准则：取综合评价向量max（pi）对应的评价指标重要性量化分级中的满意度vi作为该中心的的评价结果，最终选取满意度最高对应的中性点接地方式作为最优选择[7].

结果为小电阻接地方式满意度为v4级别满意度较高、经消弧线圈接地方式满意度为v3级别满意度一般、不接地系统接地方式满意度为v3级别满意度一般，新型接地方式满意度为v5级别满意度高，因此得出结论，新型接地方式理论上为接地方式改造的最优选择，其次是应用传统的小电阻接地方式.

4 总结

本文根据201X年南昌市配电线路故障统计数据的情况提出了评价方法，总结工作如下：

（1）总结了南昌市配电网故障的发生情况，并简要分析了消弧线圈接地的中性点系统存在的问题;针对当今城区配电网络电缆线路比例增大，配电网络自动化建设的需求，提出中性点接地方式简易选择方法—层次分析法.

（2）针对不同中性点接地方式发生故障时的系统参数特点，建立包含故障电流、弧光接地过电压和发生故障时的线路跳闸率在内的安全性能评价指标;建立Fuzzy-AHP模型，得出三大安全性能指标的隶属函数，利用层次分析法得到的相应权重，进行模糊综合评价，进行最优中性点接地方式选择.

（3）根据Fuzzy-AHP模型，经过算例验证了该方法的实用性和一定的工程参考价值，

同时也验证了本文提出的新型接地方式在配电网电缆比例结构逐渐增大的趋势下，新型接地方式在供电可靠与系统安全运行对比传统接地方式的优势，为其进行工程试验提供理论依据与参考指导.

该方法理论思路清晰，可以通过大量的实际运行数据再与实际情况相结合，有着进一步改进优化的潜力.

参考文献：

〔1〕苏继锋.配电网中性点接地方式研究[J].电力系统保护与控制，2013，41（08）：141-148.

〔2〕刘明岩.配电网中性点接地方式的选择[J].电网技术，2004（16）：86-89.

〔3〕Kingrey， L.J.， Painter， R.， Locker， A.S.. Applying high resistance neutral grounding in medium voltage systems[P]. Petroleum and Chemical Industry Conference （PCIC）， 2010 Record of Conference Papers Industry Applications Society 57th Annual，2010.

〔4〕呂军，陈维江，齐波，王晓刚，周毅.10kV配电网经高阻接地方式下过电压及接地故障选线[J].高电压技术，2009，35（11）：2728-2734.

〔5〕刘衍.开关型消弧方式激发PT过流的试验与仿真研究[A].江西省电机工程学会.2017年江西省电机工程学会年会论文集[C].江西省电机工程学会：江西省电机工程学会，2018.6.

〔6〕刘衍，龙国华，周求宽，邹阳，王羽，陈斌.开关型消弧激发PT过流的试验与仿真研究[J].高压电器，2017，53（02）：87-94.

〔7〕马春雷，龙毅，丁健，杨明波，马格土.基于模糊综合评价方法的中压配电网中性点接地方式选择方法[J].电气应用，2018，37（11）：70-74.

〔8〕肖峻，王成山，周敏.基于区间层次分析法的城市电网规划综合评判决策[J].中国电机工程学报，2004（04）：54-61.

〔9〕董仲慧.基于双层模糊综合评价的复杂产品维修决策方法[J].机械制造，2016，54（05）：93-96.