自适应信息反馈NSGA-III算法

王启翔 许峰

摘  要：为了提高NSGA-III算法求解大规模高维多目标优化问题的能力，提出了一种基于自适应信息反馈机制的改进NSGA-III算法，其基本思想是：根据信息反馈原理，将当前代第k个个体与用NSGA-III算法求得的第i个个体加权平均后作为下一代第i个个体。k的选取有指定和随机两种方式，可以根据目标函数的梯度自适应地选择。采用大规模高维测试函数对新算法进行了性能测试，并与相关算法的结果进行了比较。

关键词：高维多目标优化;NSGA-III;信息反馈;自适应;目标函数梯度

中图分类号：TP312 文献标志码：A 文章编号：2095-2945（2020）30-0020-04

Abstract： In order to improve the ability of NSGA-III to solve large-scale many-objective optimization problems， an improved NSGA-III based on adaptive information feedback mechanism is proposed. Its basic idea is： according to the principle of information feedback， the weighted average of the kth individual in current generation and the ith individual obtained by NSGA-III is taken as the ith individual in next generation. There are two ways to select k： named and random， which can be adaptively selected according to the gradient of the objective function. The performance of new algorithm is tested by the large-scale many-objective test function， and the results are compared with those of related algorithms.

Keywords： large-scale many-objective optimization; NSGA-III; information feedback; adaptive; objective function gradient

通常，有两个或三个目标的优化问题称为多目标优化问题（Multi-objective Optimization Problems，MOP），而有四个或更多目标的问题称为高维多目标优化问题（Many-objective Optimization Problems，MaOP）。多目标进化算法（Multi-objective Evolutionary Algorithm，MOEA）已被公认为求解MOP最有效的优化算法，但被用于求解MaOP时性能往往会有不同程度的下降。

MOEA主要分为两大类：一类是基于精英选择的多目标进化算法;另一类是基于多目标分解的多目标进化算法。基于精英选择的多目标进化算法中最具代表性的算法是NSGA类算法。1994年，K.Deb提出了基于非支配排序的NSGA[1];2002年，K.Deb将精英选择引入NSGA算法，提出了NSGA-II[2];2014年，K.Deb又在NSGA-II中引入参考点，提出了NSGA-III[3]。

2017年，Bi[4]提出了一種基于小生境的改进NSGA-III;2018年，M. Carvalho[5]系统研究了NSGA-III中的参考点对算法性能的影响;2020年，Gu[6]提出了一种基于信息反馈的改进NSGA-III。

本文在文献[6]的基础上，提出了一种在算法中同时采用这两种选择方式的算法，基本思路是根据目标函数的梯度自适应再选择这两种方式。采用标准测试函数对改进算法进行了性能测试，并与NSGA-III及文献[6]中算法的结果进行了比较。

1 NSGA-III算法

NSGA-III是在NSGA-II基础上发展起来的，基本步骤如下[3]：

步骤1 初始化参考点和种群（种群规模为N）。参考点根据Das和Dennis的方法[7]进行预设置。

步骤2 对父代种群Pt，通过选择、交叉、变异产生子种群Qt。

步骤3 混合Pt和Qt得到一个新种群Rt，即Rt=Pt∪Qt，其规模为2N。对Rt进行非支配排序，将其划分为不同的非支配解集（F1，F2，...，Fl，...，Fw）。

步骤4 产生一个新解集St，其方法是：从F1开始，每次移动一个非支配解集到St，直到首次出现|St|≥N，其中|St|为St中解的个数。假设Fl是首次满足|St|≥N的解集，则

步骤5 从St中选择解产生下一代父种群Pt+1。若|St|=N，则St直接被视为Pt+1。否则，首先将St＼Fl放入Pt+1，然后再从Fl中根据选择机制选取其余解。

在NSGA-III中，解的选择是基于参考点。基于参考点的选择方法如下：

首先找到种群St的理想点z*=（z1*，z2*，…，zm*），其中zi*是种群St中所有解中第i个目标函数值的最小值，然后归一化种群和参考点。此时，需要计算St中的每个解到每条参考线的垂直距离，然后用最短的距离连接解与参考点。这样，就可以在Fl中用一种新的小生境保护方法选择个体。生境数？籽j是种群St＼Fl中与第j个参考点相连的个体数。这种小生境技术的基本目的是提高NSGA-III的分布性，所以首先需要找到具有最小生境数？籽i的参考点i，然后确定Fl中有没有个体与参考点i相连。如果有个体与参考点i相连，则根据？籽i的值选择一个个体进入Pt+1。否则，这次迭代将不考虑这个参考点，而是用另外具有最小生境数的参考点重复上述操作，直到满足|Pt+1|=N。

步骤6 若满足终止条件，则输出最终的解，否则重复步骤2。

2 信息反馈NSGA-III算法

大量数值实验显示，NSGA-III在求解大规模高维多目标优化问题时性能欠佳[6]。

2019年，Wang[8]提出在启发类算法中可以引入信息反馈机制以提高算法的收敛性。据此，2020年，Zhang[9]提出了基于信息反馈机制的增强MOEA/D算法，专门用以求解大规模高维多目标优化问题;2020年，Gu[6]系统研究了在NSGA-III中如何应用信息反馈机制以提高其求解大规模高维多目标优化问题的性能。

信息反馈的基本思想是：用算法求得的结果并不直接作为t+1代的结果，而是仅作为一个中间结果，将此结果与 t代中的若干结果进行加权平均后再作为t+1代的结果。根据t代结果选取个数以及选取方式的不同，信息反馈有不同的形式。考虑到算法的复杂性，t代结果选取的个数一般不超过3，而t代结果选取的方式有固定和随机两种，即信息反馈通常有6种形式。由于基于不同信息反馈形式的算法结构类似，本文仅研究t代结果选取个数为1的情形。

当t代结果选取个数为1时，信息反馈模型定义如下[6]：

其中，Xp，Xc分别表示父代和子代个体。

在进化的早、中期，当？酌ij小于设定的阈值？着（通常取为10-2）时，意味着算法有极大的可能陷入局部最优，此时选择随机方法进行信息反馈，否则选择固定方法进行信息反馈。在进化晚期，为了防止随机方法破坏算法的收敛性，将直接选择固定方法。在编程时，通常设定总进化代数的后30%为进化晚期。

基于自适应信息反馈机制的NSGA-III（NSGA-III based on adaptive information feedback， NSGA-III-AIF）的步骤如下：

步骤1 初始化。产生初始种群P0，参考点集？撰和初始理想点Zmin。

步骤2 种群更新。

（1）对父代种群Pt，根据NSGA-III的选择、交叉、变异方法得到u;根据目标函数梯度自适应地确定信息反馈方法;代入式（1）和式（2）即得到子种群Qt。

（2）将Pt和Qt合并为Rt。

（3）按照NSGA-III中的方法，产生新解集St。

（4）按照NSGA-III中的方法，根据参考点和小生境技术，产生下一代父种群Pt+1。

步骤3 若满足终止条件，则输出最终的解，否则重复步骤2。

4 数值实验与算法性能评测

衡量多目标进化算法性能的指标分为四类[11]，考虑到本文的改进算法主要改进的是NSGA-III的收敛性，所以选用收敛性指标（GD）和综合指标（IGD）进行评测，其定义如下：

其中，O是理论Pareto最优解集，A是算法求得的Pareto Front。在GD中，di为O中第i个个体与A中个体的最小欧几里德距离。相反地，在IGD中，di为A中第i个个体与O中个体的最小欧几里德距离。显然，GD和IGD越小，表明算法取得的非支配解集逼近理论Pareto最优解集的程度越高，即算法的收敛性越好。

算法基本参数设置：种群规模100，交叉概率为0.95，变异概率为0.05，进化代数为10000。其他参数均采用相应文献中的推荐值。测试函数选用LSMOP1～9[12]。LSMOP1～9中的目标函数数m从3到15，具体为3，5，8，10，15。LSMOP1～9中含有幾十至上百个决策变量，属典型的大规模高维多目标优化测试问题。

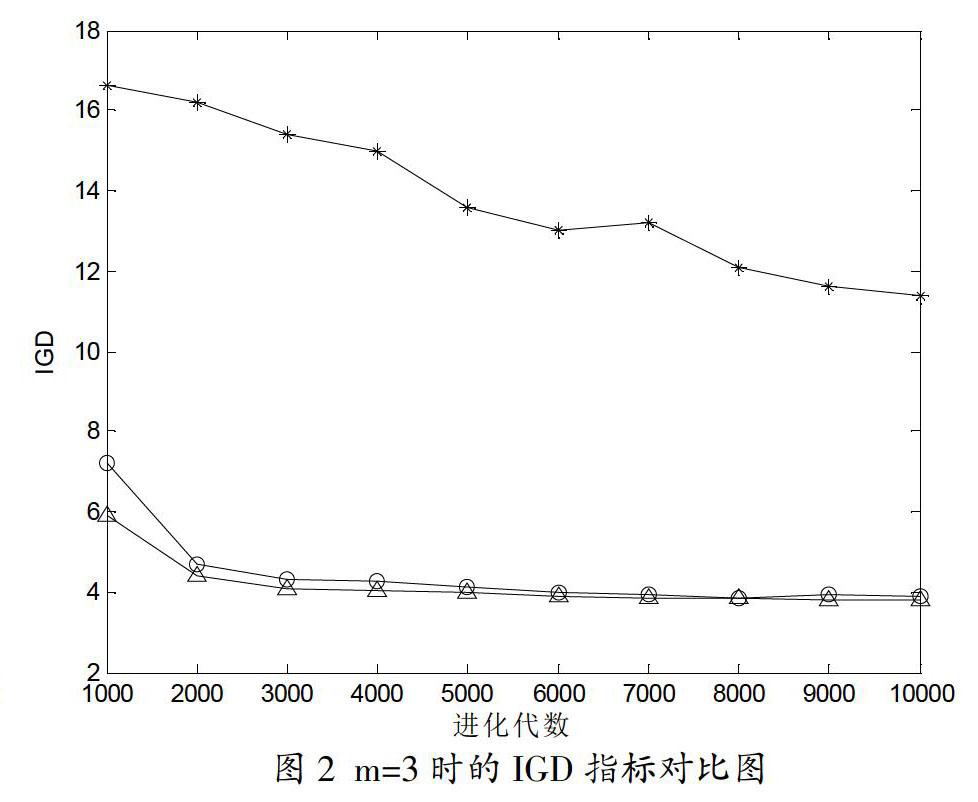
图1～图6分别给出了NSGA-III、NSGA-III-F1和NSGA-III-AIF三种算法优化LSMOP（m=3，8，15）的GD和IGD指标对比数据图。其中，*， △， ○分别为NSGA-III、NSGA-III-F1和NSGA-III-AIF的指标数据。

由于算法具有随机性，图中数据均为各算法独立运行10次的平均值。

图1～图6显示：（1） NSGA-III-AIF的GD和IGD指标明显小于NSGA-III，这表明NSGA-III-AIF在求解大规模多目标优化问题时收敛性较NSGA-III有明显提高;（2） NSGA-III-AIF的GD和IGD指标不同程度地小于NSGA-III-F1，且随着m的增大，小于的幅度也随之加大。这在一定程度上表明，基于自适应信息反馈机制的NSGA-III与基于单一信息反馈机制的NSGA-III相比，的确可以进一步改善算法的收敛性。而且，问题的维数m越高，改善的程度越明显。

5 结论

在相关工作的基础上，本文提出了基于自适应信息反馈的改进NSGA-III算法。通过对比此改进算法与NSGA-III、基于固定信息反馈的改进NSGA-III的性能指标，验证了改进算法在求解大规模高维多目标优化问题时，性能有了一定程度的提高。必须指出的是，本文的工作尚需进一步完善。比如，进化晚期的定义采用了一种人为划定的方式;由于程序所限，仅与NSGA-III和NSGA-III-F1进行了比较。

参考文献：

[1]N. Srinivas， K. Deb. Muilti-objective optimization using non-dominated sorting in genetic algorithms[J]. Evol. Comput.，1994，2（3）：221-248.

[2]K. Deb， S. Agrawal. A fast and elitist multi-objective genetic algorithm： NSGA-II[J]. IEEE Transactions on Evolutionary Computation，2002，6（2）：182-197.

[3]K.Deb， H. Jain. An evolutionary many-objective algorithm using reference-point-based nondominated sorting approach， Part I： Solving problems with box constraints [J].IEEE Transactions on Evolutionary Computation， 2014，18：577-601.

[4]Xiaojun Bi， Chao Wang. A niche-elimination operation based NSGA-III algorithm for many-objective optimization [J]. Applied Intelligence， 2017，48：118-141.

[5]Matheus Carvalho. Influence of reference points on a many-objective optimization algorithm [C]// Brazilian Conference on Intelligent Systems，2018，7：31-36.

[6]Zi-Min Gu， Gai-Ge Wang. Improving NSGA-III algorithms with information feedback models for large-scale many-objective optimization [J]. Future Generation Computer Systems， 2020，107：49-69.

[7]I. Das， J.E. Dennis. Normal-boundary intersection： A new method for generating the pareto surface in nonlinear multicriteria optimization problems [J]. SIAM. J. Optim.， 1998，8（3）：631-657.

[8]G. Wang， Y. Tan， Improving metaheuristic algorithms with information feedback models [J]. IEEE Trans. Cybern.， 2019，49（2）：542-555.

[9]Yin Zhang， Gai-Ge Wang， Keqin Li. Enhancing MOEA/D with information feedback models for large-scale many-objective optimization [J]. Information Sciences， 2020，522：1-16.

[10]刘雪东，许峰.基于目標函数变化率的混合蚁群遗传算法[J].计算机工程与应用，2013，49（18）：41-44.

[11]S. Jiang， Y. Song， J. Zhang. Consistencies and contradictions of performance metrics in multi-objective optimization[J]. IEEE Trans. Cybern.， 2014，44（12）：2391-2404.

[12]R. Cheng， Y. Jin， M. Olhofer， B. sendhoff， Test problems for large-scale multi-objective and many-objective optimization[J]. IEEE Trans. Cybern.， 2017，47（12）：4108-4121.