小学生空间观念的培养策略
蔡冬梅
(晋江市陈埭中心小学,福建 晋江 362200)
数学是研究数量关系和空间形式的科学。抽象是数学学科的一大特点,而数学学习几大区域中,图形几何的内容尤为抽象。在小学数学中,如何设计有效的学习活动,培养小学生的空间观念?如何通过图形与几何的学习,落实培养学生空间观念的目标?下面谈谈几点教学活动策略。
一、联系生活,设计问题情境
在数学教学中,对抽象的学习内容,如果能合理选择直观的教学方式,可以使复杂的问题简单化。巧设问题情境,可以让学生产生身临其境的感觉,从而激发兴趣,引起思考。数学教学要体现数学来源于生活又应用于生活的特点,使学生感受数学与现实生活的密切联系。[1]
例如,在黄爱华老师经典的课例《圆的认识》中,从学生的生活经验出发,课的起始就把问题聚焦于“井盖为什么是圆的”,让学生基于生活经验,在探究中明确,井盖中总有一条最长的线(圆的直径)卡在井口,使它不会掉下去,从圆的直径开始串起整节课的学习活动。华应龙老师在教学《角的认识》时,从学生最熟悉的滑滑梯问题情境入手,提问:滑梯应该设计成哪个角度合适呢?教师应善于在生活中寻找数学素材,将其提炼成数学问题,数学知识在学生眼中就变得鲜活、有生命力。诸如此类的问题情境设计,拉近了抽象知识与学生思维间的距离,对图形几何的教学、发展学生的空间观念尤为重要。
二、提供直观材料,形成空间表象
空间观念的形成,离不开大量的实践活动。如何让抽象的数学知识变得可视、可感?这就需要教师根据教学内容,提供直观材料,通过对教具和学具的直接观察,将抽象的问题直观地展示出来。在这一过程中,多种感官参与学习活动,不仅能使学生学得生动活泼,而且对知识的理解更深刻,从而认识概念,形成空间表象。[2]
例如,《认识厘米》是一年级学生认识度量单位的起始课。如何让学生形成“量”感?笔者先让学生观察尺子,再通过小组合作,利用许多1 厘米长的牙签、木板等材料制造一把尺子。在这一过程中,随着1 厘米牙签的有序摆放,学生不断进行对量的累加,5 厘米里含有5 个1 厘米的认识就自然到位了。在后续的练习中,设计用没有刻度的尺子测量铅笔的长,学生产生认知冲突:这能用吗?通过讨论,有学生提出可以对尺子进行改造,标上数字;有学生提出可以直接利用尺子上的长竖线测量,这样测量的关键点就凸显出来了。只要明确一个基本单位,以这个单位为标准,通过计数或累加,就能得到测量的结果。教师也可以寻找学生手中的断尺(没有零刻度),以断尺为研究材料,测量铅笔的长度,和上面用没有刻度的尺子测量的设计可谓是异曲同工之妙。
再如,四年级学面积概念时,教师提供1 平方厘米的小图片,让学生测量图形面积。再从铺图形的活动中,进一步感知面积的意义。用不同方式——铺满图形,铺一行一列,铺在心里(测量长与宽)。通过三个层次,学生顺利地悟出长方形面积计算公式的道理。在这一教学过程中,操作与观察相结合,丰富数学感知,学生把这些面积单位的表象熟记于心,从而正确应用来解决问题。
三、发展想象,凸显数学本质
史宁中教授指出,“空间观念的本质就是空间想象力”。想象是发展学生空间观念的重要途径。要为学生精心设计激发想象力的活动,将想象、思考、推理和分析综合运用,才能有效地促进学生空间观念的形成。
例如,推导长方形面积计算公式,设计课堂学习活动时,从铺有形的砖到无形的砖,其实也是发挥学生的想象,把砖铺在心里。学生有了“铺砖”意识,把求长方形面积等同于铺砖,就不会和求长方形的周长问题产生混淆。推导长方体体积计算公式时,在延续铺砖问题(求底面积)的基础上,演变成“盖楼”问题,先铺一层砖,再一层一层地往上搭。通过通俗易懂的语言,把冰冷的数字变得有温度、生活化。在练习巩固阶段,可设计这样的习题:“一个体积是24 立方厘米的长方体,它的长宽高可能是多少?”借助盖楼的模型,引导学生通过想象,先铺一层长为4 厘米、宽为2厘米的砖,再往上搭2 层……将知识化难为易、化抽象为直观,学生积累数学活动经验,发展空间观念。
四、变式练习,提升数学思维
平时学生最不愿意做的习题是按照公式计算图形的面积、体积等问题。例如,计算无盖金鱼缸的表面积,题目里出现了长85cm、宽44cm、高60cm 的信息,问题是至少需要多少平方米玻璃?题目中需要单位换算,可是大部分学生熟视无睹,算出了表面积为1万多平方米的答案后,也并未意识到自己的错误。说明学生对问题里的数字“无感”,究其原因,一旦学习了某个计算公式,学生接触的就是常规的计算公式题,所以表现得麻木、应付。教师应针对知识点的特征,设计变式练习,以调动学生学习的积极性,并充分发挥练习的巩固、提升知识经验的作用。
例如,教学《圆的面积》一课后,可以设计这样的变式题:如图1,只知道这个阴影部分的面积为10 平方厘米,圆的面积是多少?学生发现,题目条件不充分,半径不能求出来,这个圆的面积怎么计算出来?教师提醒学生认真观察图形,换一个角度思考问题,已知阴影部分的面积还蕴含着什么信息?学生通过观察、讨论后顿悟,将求半径问题转化为求半径的平方,圆的面积等于10 乘3.14 的乘积,顺利地解决了问题。
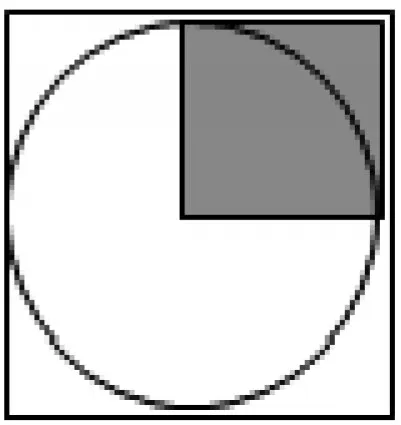
图1
当学生认识长方体的特征后,教师提出以下问题:
问题1:4 个棱长为1 厘米的正方体,能拼成大一点的正方体吗?
有学生赞同,有学生反对。这时,请赞同的学生利用正方体摆一摆,通过动手操作,发现自己的错误。
问题2:一个棱长为3 厘米的正方体,可以切成几个体积为1 立方厘米的小正方体?
让学生在交流中辨析,找到正确答案,从而为学习正方体的体积计算公式搭桥铺路,奠定良好的知识基础。
问题3:一个棱长为3 厘米的正方体,表面先涂上油漆,切成一个个1 立方厘米的小正方体,三面都涂油漆的小正方体有几个?
先请学生试着想象,然后通过摆小正方体、画草图的办法,验证想法、获取答案,从而进一步体会长方体的特征,发展空间观念。
一道命题就像一张“通行证”,指向的是学生发展的方向和路径。[3]这样的变式练习,充分调动学生的数学思考,激起探究欲望,从而锻炼思维,获得能力,提升水平。
总之,空间观念的培养是一个包括观察、想象、比较、综合、抽象分析的过程。[4]在课堂教学中,联系生活,设计问题情境,在情境中自然地拉近数学与生活的距离。提供直观、感性材料,发挥直观经验的作用,帮助学生建构概念、形成表象,变机械学习为有意义的学习。加强动手操作和实验观察相结合,发挥想象作用,凸显数学本质。设计变式练习,让学生在运用概念解决问题时,将知识融会贯通,巩固、完善、拓展概念,提升数学思维。只有精心设计教学活动,把抽象的数学知识变得触手可及,把枯燥乏味的数学学习过程变得生动活泼,学生才能在这一过程中掌握数学概念、感悟数学思想、发展空间观念。

