开孔层合板双轴拉伸渐进损伤分析与试验验证
徐传奇,温卫东,郭俊华
(南京航空航天大学 a. 能源与动力学院; b. 机械结构力学及控制国家重点实验室,江苏 南京 210016)
0 引言
树脂基复合材料具有比重小、抗疲劳、耐腐蚀等优点,目前已在航空航天、能源机械等领域代替传统的金属材料,获得了较为广泛的应用。仅飞机而言,复合材料用量已从占机体总重的2%~3% 增加至10%~15%,在更先进机体结构上,其用量甚至高达40%~60%。在设计加工复合材料结构件时,某些部位如机械连接处、维护口盖等位置,必不可少地要在结构件上开孔。在工作状态下,复合材料构件常处于多轴应力状态,这使得开孔部位应力分布更加复杂、应力集中更加严重,可能引起复合材料纤维断裂、基体损伤及分层等多种破坏,进而威胁整体的结构安全[1]。因此,为提高复合材料结构件承载力与耐久性,需对含孔复合材料在多轴载荷状态下的承载性能与破坏特征深入研究。
近年来,含孔复合材料层合板在不同载荷作用下的破坏行为受到了国内外研究者的广泛关注。肖梦丽等[2]结合试验分析建立拉伸载荷下合理的二维有限元模型,并分析对比不同失效准则对剩余强度的影响,发现其可较准确预测含孔层合板的剩余强度。朱建辉等[3]基于逐渐损伤分析方法,建立压缩载荷下含孔层合板的三维有限元模型,可模拟压缩载荷下损伤直至失效的过程。CHANG K Y等[4]提出了复合材料含孔层合板在拉伸载荷作用下的逐渐损伤模型,数值模拟结果与试验结果吻合较好。MAA R H等[5]基于连续损伤力学理论,提出包含3种损伤模式的层内损伤模型,研究计算开孔复合材料层合板的单轴拉伸极限破坏强度。
目前复合材料在双轴载荷作用下的力学行为也受到广泛的关注。陈秀华等[6]基于非线性渐进失效理论与Hashin失效准则,研究CFRP单向板与层合板在双轴载荷下损伤初始状态与最终失效应力。RASHEDI A等[7]通过数值模拟与试验分析,对比玻璃纤维增强复合材料在单轴和双轴拉伸下的破坏形式,建立了一种精确预测GFRP破坏形式的新模型。
本文采用逐渐损伤模型研究含孔复合材料层合板在双轴拉伸载荷作用下的承载能力与破坏行为。以十字架结构为研究对象,分析对比不同加载比对其双轴拉伸强度与破坏行为的影响,并通过相应的试验分析,验证此模型的准确性、可靠性。
1 渐进损伤分析
1.1 逐渐损伤模型
逐渐损伤模型主要由应力求解分析、单元失效判断准则及损伤材料性能退化3大部分组成。本节利用ANSYS软件建立三维有限元模型,并进行应力分析,利用Hashin失效准则判断有限元单元的失效,在材料损伤失效之后,采用折减刚度的方法计算损伤材料的性能退化。
a) 应力求解分析
假设载荷P由第n-1步增加到第n步,即P=nP时,由于层合板内无体积力,则平衡方程为:
nσij,j=0 (i,j=1,2,3)
(1)
此时力的边界条件可表示为:
(2)
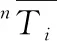
假设载荷由第n-1步增加到第n步时,应变增量为Δεij,位移增量为Δuij,则根据虚位移原理,式(2)可变为:
(3)
应力增量Δσij与应变增量Δεij可分别表示为:
nσij=n-1σij+Δσij
(4)
(5)
将式(4)代入式(3)中,可得:
(6)
假设每一步增加载荷足够小,以确保应力-应变关系按线性关系处理,则:
Δσij=n-1CijklΔεkl
(7)
式中n-1Cijkl为第n-1增量步中的模量,其取决于每个载荷增量。将式(5)与式(7)代入式(6)可获得应力与位移增量的表达式:
(8)
随着载荷的增加,材料将出现损伤,这些损伤会导致材料性能变化,即材料模量值发生变化,此时应力、应变也将重新分配,需重复使用式(8)进行计算,直至层合板失效。
b) 双向载荷下失效准则
材料失效准则采用三维Hashin失效准则[8],可较好地预测层合板的失效模式和各失效模式的扩展过程。其表达式如下:
1) 纤维拉伸失效(σ11>0)
(9)
2) 纤维压缩失效(σ11<0)
(10)
3) 基体拉伸失效(σ22>0)
(11)
4) 基体压缩失效(σ22<0)
(12)
5) 纤维-基体剪切失效(σ11<0)
(13)
6) 法向拉伸失效(分层)(σ33>0)
(14)
7) 法向压缩失效(分层)(σ33<0)
(15)
式中:σii、σij分别为单层板各主方向及相应面内的切应力;Xn、Yn、Zn、Sij为单层板各主方向及相应面内的剪切强度;n为T时表示拉伸;n为C时表示压缩。
c) 双向载荷下材料退化准则
随着载荷逐渐增加,层合板将出现损伤,损伤区域材料的性能将发生退化。采取CAMANBO P P等[9]提出的退化方式,认为损伤区域的刚度退化可用内部状态变量表示,可以将其看作刚度折减系数。退化具体方式如下:
1) 纤维拉伸、压缩失效:E1、E2、E3、G12、G23、G13、V12、V13、V23发生刚度退化,刚度折减系数为0.07。
2) 基体拉伸、压缩失效:仅E2发生刚度退化,刚度折减系数为0.14。
3) 纤维-基体剪切失效:G12、V12发生刚度退化,刚度折减系数为0。
4) 分层失效:E3、G13、G23、V13、V23发生刚度退化,E3刚度折减系数为0.14,G13、G23、V13、V23刚度折减系数为0。
1.2 有限元模型
参照文献[10]中的有限元模型,采用含孔开缝十字架试验件,其具体几何尺寸如图1所示。
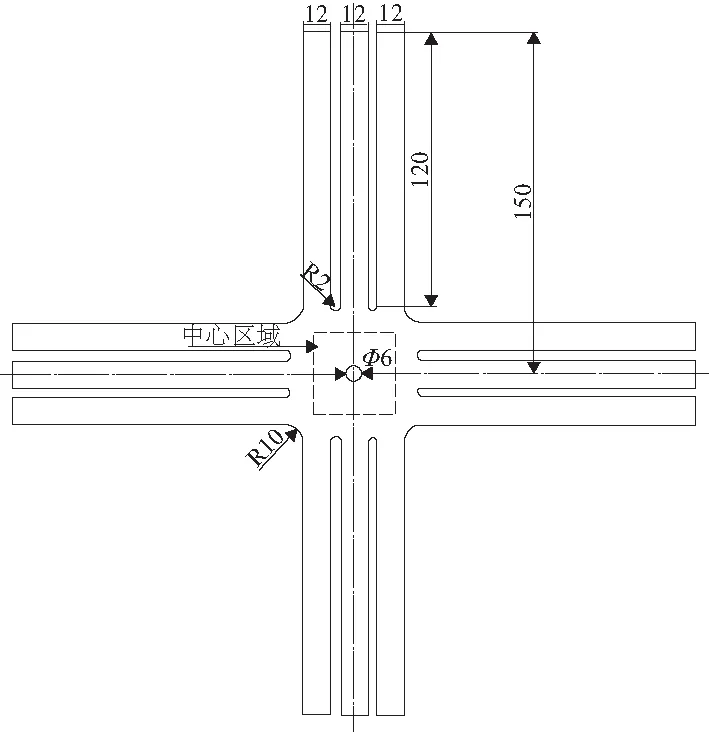
图1 十字架尺寸设计图
中心区域网格划分如图2所示。
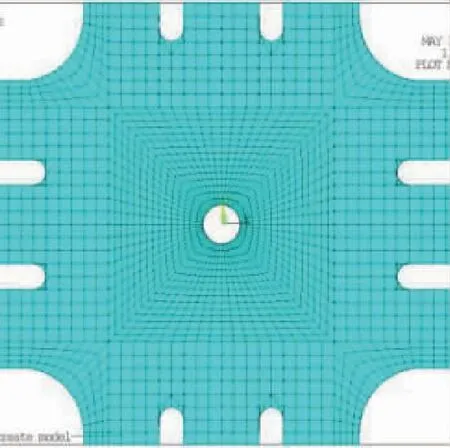
图2 中心区域网格划分
由于圆孔周围应力集中,所以对圆孔孔周进行局部网格加密。所选取单元类型为soild185,在模型左端与下端分别施加x、z方向与y、z方向约束,右端与上端施加位移载荷。
1.3 材料参数选取
采用碳纤维/环氧复合材料,材料的基本属性如表1所示,所选择铺层顺序为[0/90]4s。

表1 材料基本属性表 (除V12外其他单位均为MPa)
1.4 损伤失效分析
采用本文的渐进损伤分析方法,对3种双轴加载比下的含孔十字架层合板进行逐步损伤失效分析,各损伤分类如图3所示。3种加载工况下表面0°层与内部90°层的极限损伤失效图如图4-图6所示(本刊黑白印刷,有关疑问咨询作者)。

图3 损伤分类图
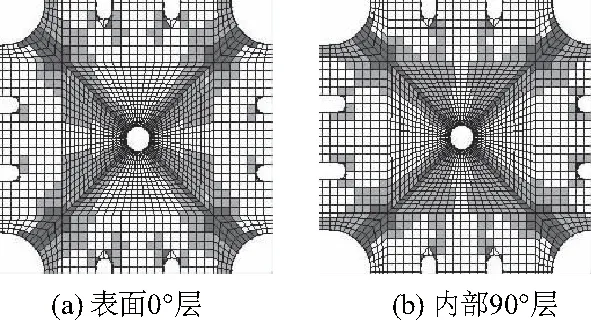
图4 加载比Fy∶Fx=1∶1时极限损伤失效
如图4所示,对于加载比为1的情况,0°层与90°层的极限失效损伤都包含基体与纤维损伤,其主要破坏形式皆为纤维与基体损伤从孔端沿45°向十字架倒角处扩展,而0°层与90°层的基体损伤都会延伸至竖直加载臂的缝端。
如图5所示,对于加载比为2的情况,0°层基体大部分损伤,纤维损伤主要从孔端延伸至水平加载臂的缝端,倒角处也存在些许纤维损伤。而90°层主要受纤维损伤控制,纤维损伤扩展至水平加载臂的缝端,伴随部分基体损伤向上端倒角处扩展。
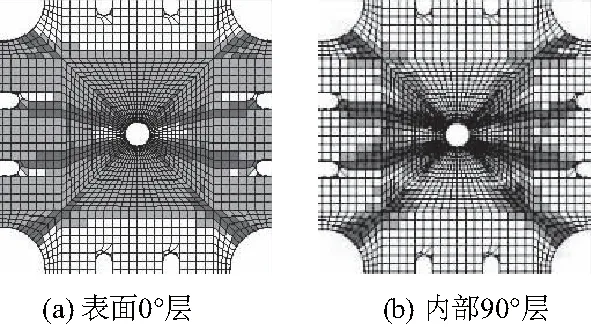
图5 加载比Fy∶Fx=2∶1时极限损伤失效
如图6所示,与加载比为2时的损伤类似,在加载比为3的0°层与90°层,纤维损伤主要从孔端延伸至水平加载臂的缝端,只在倒角位置出现部分纤维与基体损伤。
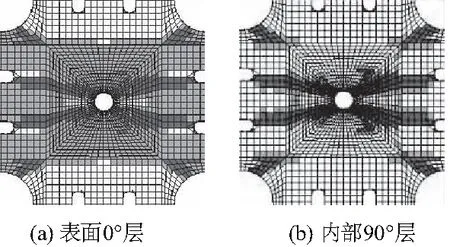
图6 加载比Fy∶Fx=3∶1时极限损伤失效
2 试验验证
张江涛等[10]对含孔正交层合板进行了双轴静拉伸试验,试验件尺寸与材料属性等均与计算模型相同。试验获得的加载位移曲线与计算结果对比、试验与计算的强度结果对比及试验所获得的试件表面断口图展示如下。
2.1 加载-位移曲线
在3种加载比下,试验获得的载荷-位移曲线与有限元模拟所得的载荷-位移曲线作对比如图7-图9所示。
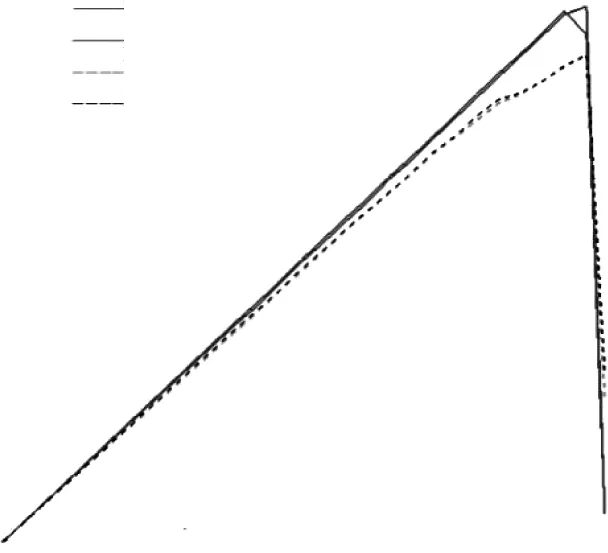
图7 试验载荷-位移曲线与有限元 结果对比(Fy∶Fx=1∶1)
由图7可见,载荷与位移的曲线在加载前期基本呈线性,随位移增加曲线斜率也逐渐降低,在达到极限状态时曲线陡降,即发生脆性破坏。
图8所示为加载比为2的情况,x向与y向的载荷-位移的曲线初始也基本呈线性,在试验加载中后期由于界面脱粘,y向载荷会出现突降现象[10],随后加载曲线与有限元模拟曲线会基本重合。
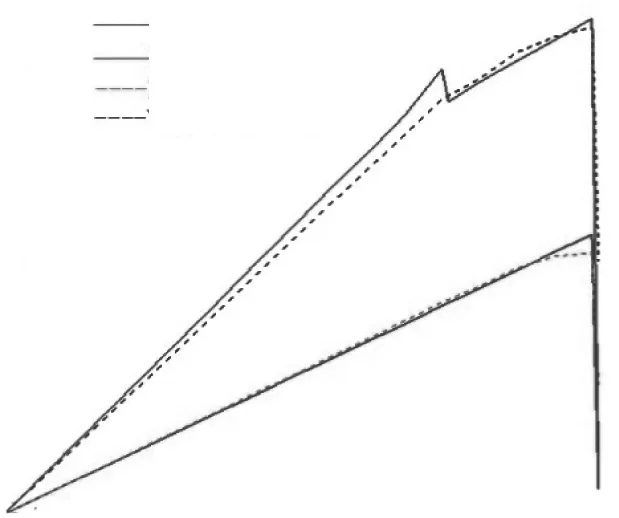
图8 试验载荷-位移曲线与有限元 结果对比(Fy∶Fx=2∶1)
图9所示为加载比为3的情况,与加载比为2时的特征类似,但其发展更迅速。试验加载中后期由于界面脱粘,y向载荷会出现稍微突降现象[10]。而在y向载荷达到极限时,x向拉载由于较小,未达到层合板极限承载能力,所以仍可随位移增加一段时间。
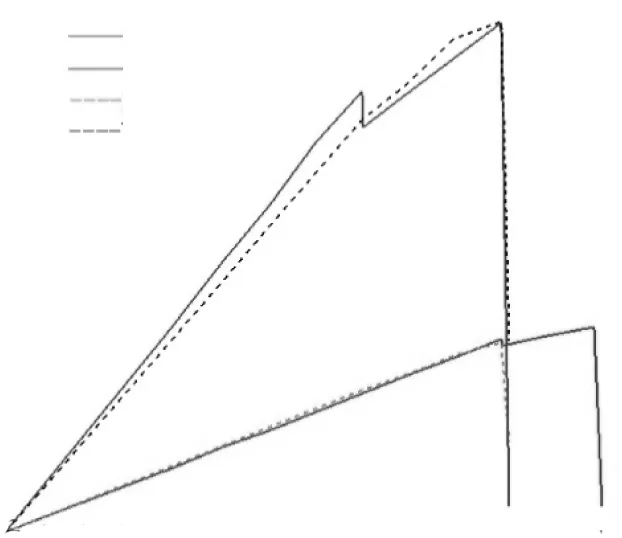
图9 试验载荷-位移曲线与有限元 结果对比(Fy∶Fx=3∶1)
2.2 强度结果分析
3种加载工况下双向拉伸强度的试验与有限元计算值对比如表2所示。
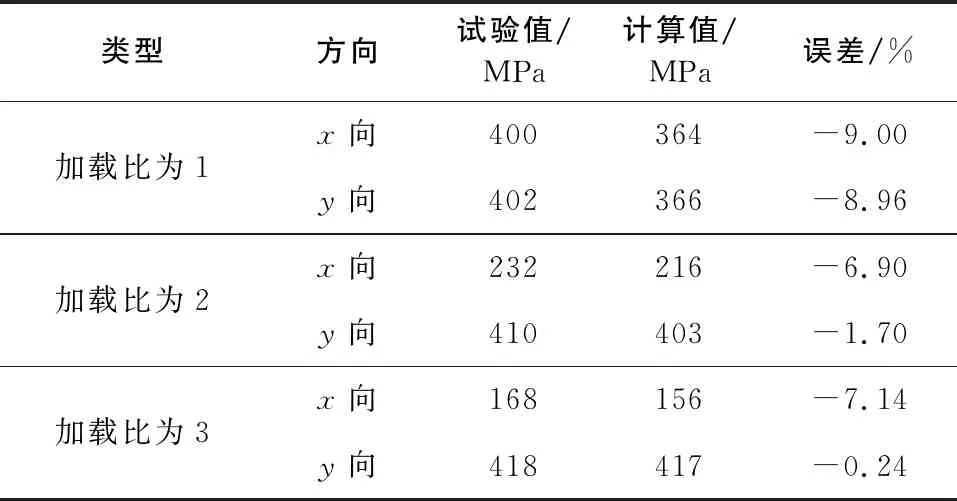
表2 双向拉伸强度试验与计算对比
由表2可见:随着加载比的增加,十字架试件主拉方向的拉伸强度也不断增加;不管是x向还是y向强度,本文预测值与试验值误差都在9%以内,可见预测精度较高,证明此逐渐损伤模型的可靠性。
2.3 试件断口破坏
各加载比下试验件的表面破坏图[10]如图10所示。

图10 试验件表面破坏图
由图10(a)可见,加载比为1时,表面基体裂纹会向上扩展至加载臂的缝端,右上沿45°出现纤维破坏至倒角处。图10(b)中,加载比为2时,表面裂纹扩展至左侧水平加载臂缝端及右上45°倒角处。图10(c)中,加载比为3时,表面裂纹主要向水平加载臂的缝端扩展。综上,各加载工况下试验件破坏形式与有限元模拟获得的损伤失效形式匹配较好,再次验证本文模型的有效性。
3 结语
本文采用三维逐渐损伤模型,研究对象为开缝的中心开孔十字架试件,分析不同加载比对其双轴拉伸强度与损伤行为的影响,获得主要结论如下:
1) 对于等双轴加载,试验与有限元计算的载荷-位移曲线变化趋势较一致,且基体损伤都会扩展至上加载臂的缝端。
2) 对于非等轴加载,试验主方向的载荷-位移曲线在加载过程中存在突降现象;随载荷比增加,主拉方向的损伤发展更快,导致两方向拉力比逐渐降低;主要损伤形式的扩展方向更垂直于主拉方向。
3) 随着加载比的增加,含孔正交层合板主拉方向的拉伸强度呈现逐渐增加的趋势。
4) 本文所建立的层合板三维渐进损伤分析模型,计算获得的极限载荷与试验值之间最大误差在9%之内,且预测值都低于试验值,工程应用方面偏安全。

