多任务模糊聚类驱动的多任务TSK模糊系统模型

蒋亦樟，华 蕾，张 群,2，钱鹏江，夏开建,3,4

1.江南大学人工智能与计算机学院,江苏无锡214122

2.江南大学图书馆,江苏无锡214122

3.苏州大学附属常熟医院信息科,江苏苏州215500

4.中国矿业大学信息与控制工程学院,江苏徐州221116

经典的机器学习方法已广泛用于如聚类、分类、回归[1]等实际应用.很多方法因其简单性和优越性而闻名，如k均值[2-3]、模糊c 均值（FCM）[4-6]、神经网络[7-8]、支持向量机[9-10]、模糊系统[11-17].但这些经典方法都面向单任务学习场景，不能有效满足当前多任务学习场景的需求.以生化发酵过程[18]为例，其谷氨酸发酵过程需要同时处理多个任务.这种学习场景就是一个典型的多输入多输出（multiple-input-multiple-output,MIMO）系统，对应的数据集可分解为多个多输入单输出（multiple-input-single-output,MISO）的数据集.如果将每个MISO数据集视为一个任务且所有任务具有相同的输入但每个任务的输出不同，那么经典的单任务建模方法（如传统的Takagi-Sugeno-Kang(TSK)模糊系统[14]）可以独立地对这些MISO 数据集进行建模并取得一定的性能.但相较于用多任务学习机制的模型而言，这些经典的单任务学习模型显得效率低[19-21].

对于一个明确的多任务场景问题，一种有效地方式是设计出新的具有多任务协同学习能力的学习框架.当前，针对不同的机器学习问题，提出了各种多任务学习机制并已广泛应用于聚类[22-24]、分类[20-21,25-26]、回归[16,17,27-29]问题中，本文工作重点将放在回归问题上.模糊系统作为一种经典的回归方法，因其可解释性和学习能力而广泛应用于智能控制、信号处理、模式识别[14,15,30-34]等领域.

众所周知，模糊系统建模优化通常包括前件参数优化和后件参数优化两个步骤.为了将多任务学习机制整合到以上两个步骤中，本文首先提出了一种多任务模糊c 均值（multi-task fuzzy c-means,MT-FCM）聚类算法用于优化多任务TSK模糊系统（multi-task TSK fuzzy system，MT-TSK-FS）的前件参数.所提出的多任务模糊c 均值聚类算法具备在每个任务上得到最优的共享前件参数和独立前件参数用于后期多任务模糊系统的构建.其次，设计了一种具备多任务协同学习机制的后件参数优化方法，用于优化多任务TSK 模糊系统的后件参数.该方法源自经典的L2-范数TSK 模糊系统后件学习策略[16-17]，通过融入新的多任务协同学习机制改进了目标函数最终用于优化多任务TSK 模糊系统的后件参数.最后，基于优化的前件参数和后件参数构建出具体的多任务TSK 模糊系统用于实际应用.大量的模拟实验和真实数据实验表明本文所提之多任务TSK 模糊系统具有更加的性能以及良好的解释性.

1 相关工作

基于聚类的模糊系统是目前常用的TSK 模糊系统，模糊规则的前件和后件参数时往往分阶段计算.模糊规则的前件参数通过聚类结果计算得到，模糊规则的后件参数通过一定的学习策略得到.由于常规聚类是将数据空间的划分视为单个任务，因此单任务聚类构建的规则前件也是单任务的，如文献[35-37].单任务模糊系统只能对各个独立的任务分别进行建模学习，是因为无法充分利用每个任务数据之间的联系.面对多个任务的建模场景，单任务模糊系统的性能往往不能令人满意.为了提升模型在多任务建模中的性能，一些研究者提出了多任务模糊系统.如文献[38]将动态集成选择的方法引入TSK 模糊系统，构成含多个分类器的动态系统，其动态生成和集成分类器的机制可以为特定分类对象选择合适的分类器.文献[39]提出了基于模糊集的在线多任务学习进化系统，该系统使用数据流驱动的递归更新信息粒，并将它解释为If-Then 模糊规则的前件部分.信息粒的交集则解释为If-Then 模糊规则之间的稀疏结构关系图和多任务学习中任务间的关系桥梁.文献[40]提出了一种紧凑的模糊规则和共享的结果参数的多任务模糊系统，该方法通过在模型的学习准则中设计新的稀疏正则化来考虑模糊规则的约简和任务间的参数选择，同时实现了任务间关系的整合.文献[16-17]则将传统的TSK 模糊系统扩展到多任务学习场景的方法.在文献[16]中，基于经典的L2-范数TSK 模糊系统，提出了一种称为MT-TSK-FS 的多任务TSK 模糊系统.多任务学习机制用于重构目标函数以学习不同任务的结果参数.新的目标函数不仅可以利用每个任务的独立信息，而且可以有效地利用任务间的相关信息.在文献[17]中，低维子空间假定为在所有任务之间共享，因此所有任务的隐藏相关信息都用于多任务学习.因此通过挖掘上述常见的隐藏结构，提出了一种称为MTCS-TSK-FS 的多任务TSK 模糊系统模型.这两种多任务学习策略仍然存在一些不足：1）MT-TSK-FS 和MTCS-TSK-FS 都共享TSK-FS 模型的先验参数，对于每个任务显然与多任务学习机制相矛盾，而更合理的是每个任务的前提都应包含与其他任务共享的公共部分和单个部分；2）文献[16-17]中的结果参数的学习仍然很薄弱，要服从共享的先验参数；3）模糊系统的可解释性受共享前件参数的阻碍，导致规则的IF部分对所有任务都是相同的，因此对于不同的任务生成的模糊规则的可解释性变得很弱.为了克服上述局限性，本文构想了一种基于多任务聚类的多任务TSK-FS 建模方法，需要建立一个多任务学习机制来学习相应的参数.总体上，提出了一种新的多任务TSK 模糊系统学习框架，并通过为模糊系统的前件参数和后继参数提供多任务学习来进行区分.表1总结了所提方法与相关工作的简要比较，例如经典的单任务TSK模糊建模方法[35-37]与我们已提出的多任务TSK 模糊建模方法[16-17].

表1 基于TSK 模糊系统的回归方法Table 1 TSK fuzzy systems based methods for regression

2 多任务模糊c 均值算法

模糊c 均值算法（fuzzy c-means，FCM）是传统单任务聚类的经典算法之一[4-6].本文将以此模型作为基础，提出一种多任务模糊c 均值聚类算法（multi-task fuzzy c-means,MT-FCM）.

2.1 经典的单任务FCM 算法

经典FCM 算法的主要目标函数为

式中，xj为第j个样本，vi(vi1,···,vik)为第i个聚类中心，µij为第i个样本隶属于第j个类中心的程度，模糊指数m满足条件m >1.通过使用拉格朗日优化来最小化式(1)，可得出中心vi和模糊隶属度µij的更新规则为

基于迭代更新学习原理，可得最佳的隶属度U和类中心V.

作为一种经典的数据驱动的类别划分方法，FCM 算法在不同的应用中获得了较大的成功[14-17,41-42].但经典的FCM 算法仅针对传统的单任务聚类场景而设计，不能直接用于同时处理多任务场景中的所有数据集.因此，在面对多任务聚类问题时，一种常见的解决方案是用经典FCM 算法对多任务数据集中每个任务的数据进行单独的聚类.这种做法由于算法自身的限制性导致任务间的关联信息无法被使用，进而造成最终聚类效果普遍不佳的情况.因此，本文提出了一种用于多任务场景的多任务FCM 聚类算法.

2.2 多任务模糊c 均值算法

在多任务聚类问题中，若给定一个包含K个任务的多任务数据集，每一个任务对应Nk个数据，该数据集可表示为Xk={xi,k,i=1,···,Nk}，xi,k ∈Rd.为了从多任务数据中提取共有和私有信息及个人信息，在FCM 框架中引入多任务学习机制，本文重新设计了新的目标函数为

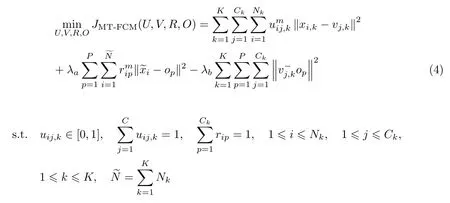
式中，Ck和P分别为独立类中心和公共类中心的总数；xi,k为第k个任务中的第i个样本；表示包含所有任务数据样本中的第i个数据样本；Uk=[µij,k]Ck×Nk为第k个任务的私有模糊划分矩阵；Vk=[v1,k,···,vCk,k]为第k任务的私有聚类中心；R=[r1]为所有任务的公有模糊划分矩阵；O=[o1,···,oP]为所有任务的公有聚类中心；λa和λb是两个可人工调节的正则化参数，用于控制不同项对整体目标函数的影响，可用交叉验证的方式来确定.

接下来，可以求解方程(4)以获得多任务FCM 聚类的最优解.式(4)的拉格朗日函数可以表示为

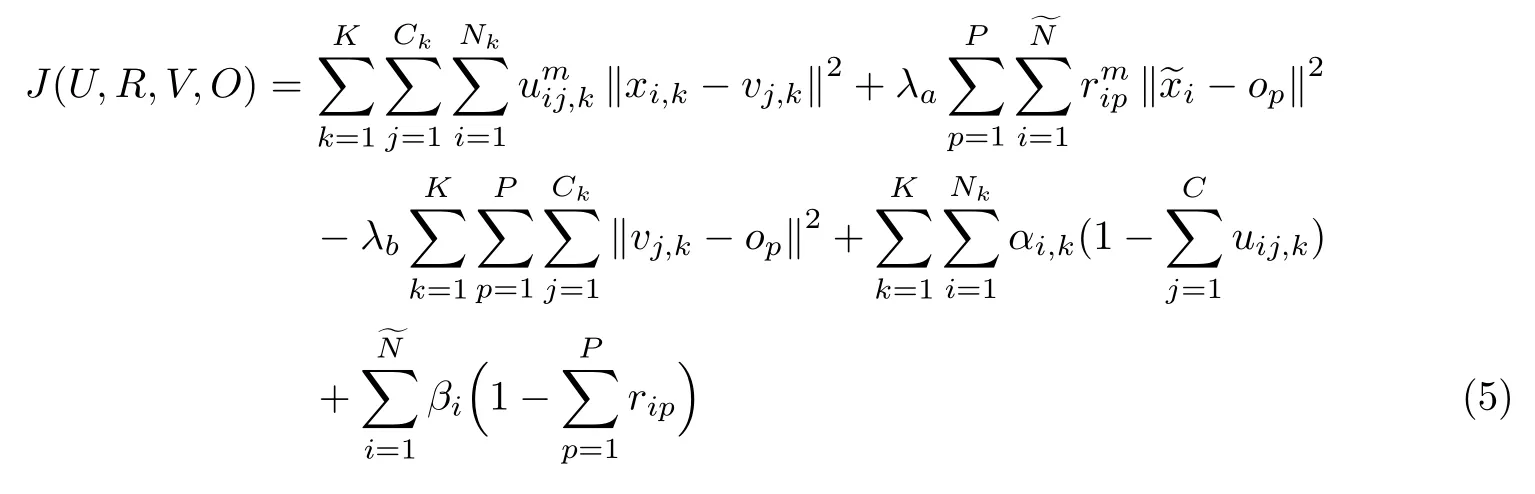
通过对各项求导数，最终可得到各参数的优化更新公式如下：

根据上述更新公式，本文所提出的MTFCM 算法的具体计算步骤可总结如下：

步骤1给定K个任务，需预先设定Ck(2CK < Nk)，P(2P <)，收敛阈值ε，模糊指数m，正则化参数λa(λa >0)，λb(λb >0)，最大迭代次数T；此外，还需初始化每个任务的独立聚类中心vj,k和所有任务的公共聚类中心op，设置迭代次数的初始值s=1.

步骤2用式(6)更新私有模糊隶属度

步骤3用式(7)更新私有聚类中心

步骤4用式(8)更新公有模糊隶属度

步骤5用式(9)更新公有聚类中心

步骤6如果|J(s+1)−J(s)| < ε或迭代次数l > T，迭代终止，否则使l=l+1 并跳转到步骤2.

3 多任务模糊c 均值算法驱动的多任务TSK 模糊系统

3.1 系统架构

为了克服我们已经提出的两种多任务TSK 模糊系统建模方法所存在的局限性[16-17]，本文将基于提出的多任务模糊c 均值聚类算法构建一种新的多任务TSK 模糊系统模型（multitask fuzzy c-means based multi-task TSK fuzzy system,MTFCM-MT-TSK-FS），以实现以下两个目标：

1）在文献[16-17]中，每个任务的模糊系统前件参数均是私有化的无公有参数，MTFCMMT-TSK-FS 方法将首次提出公有前件参数和私有前件参数并用的全新形式.

2）通过更有效的多任务学习机制，进一步优化模糊系统后件参数的学习策略，进而增强模糊规则的可解释性.

为了实现上述目标，可以借助图1来理解MTFCM-MT-TSK-FS 的构建框架.

图1 多任务模糊系统：多任务学习策略Figure 1 Fuzzy systems for multiple tasks:multi-task learning strategy

图1显示了MTFCM-MT-TSK-FS 模型的框架.对于这个多任务模糊系统构建框架，每个任务的模糊规则定义如下：

1）所有任务的公有模糊规则

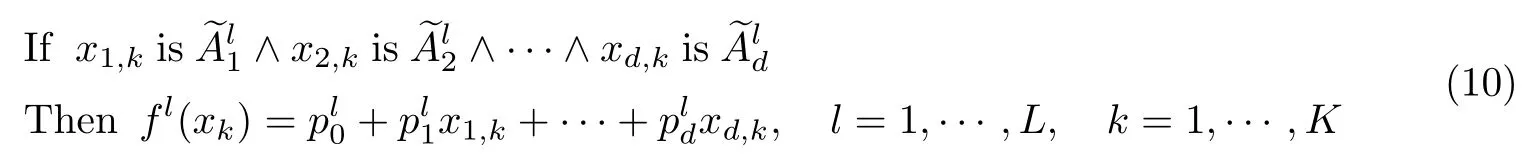
2）第k个任务的私有模糊规则

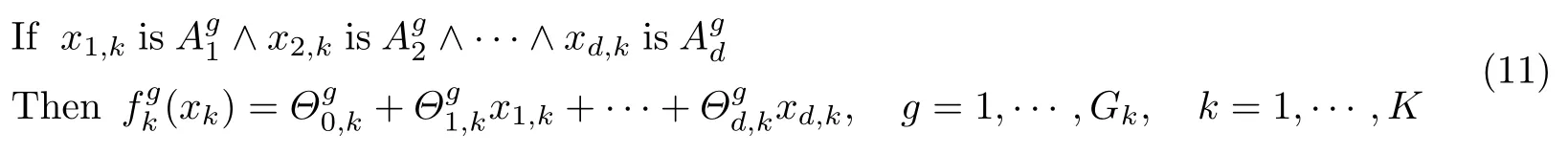
式(10)和(11)中，xk为第k个任务的样本，表示输入变量xi为所有任务的第l个公有模糊子集；表示输入变量xi,k为第k个任务的第g个私有模糊子集；Gk表示第k个任务的单个模糊规则的数量；∧为模糊合取运算符.根据模糊推理，最终第k个任务的多任务TSK 模糊模型的输出可表示为

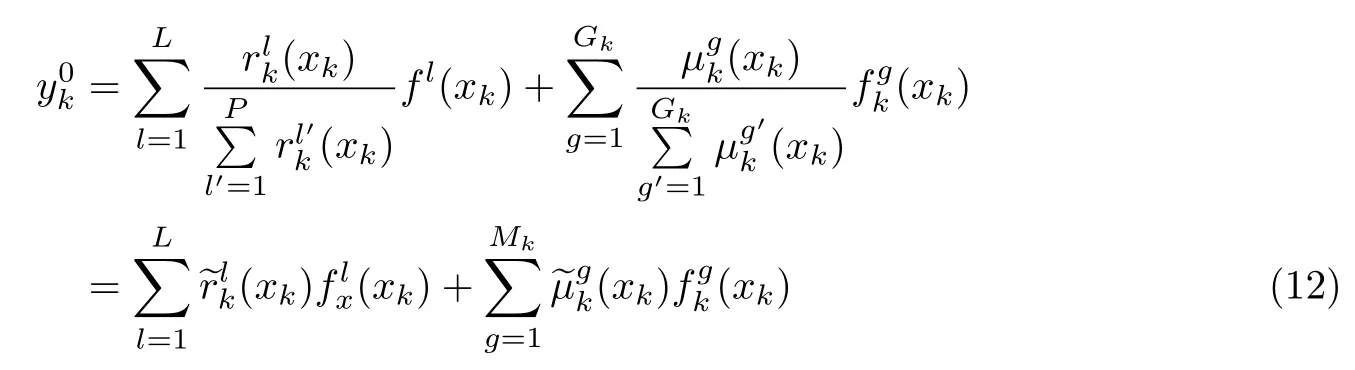
式中，和表示模糊隶属函数，和表示为归一化后的模糊隶属度，和分别与任务k中公有和私有模糊集和相关联.

3.2 学习算法

模糊系统的学习包含前件和以及归一化后的和，其计算方法如下：

然后，本文选用高斯隶属度函数作为模糊隶属度函数

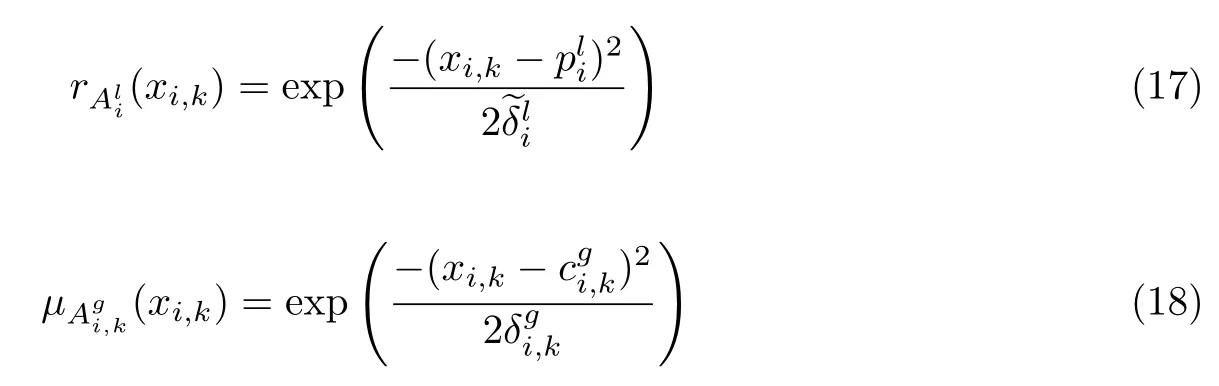
式中，rjl表示所有任务中第j个数据点隶属于第l个聚类中心的公共模糊隶属度，ujg,k表示第k个任务中第j个数据点=(xj,k,yj,k)=(xj1,k,···,xjd,k,yj,k)T隶属于第g个类的私有模糊隶属度，h和hk为自定义参数，可以手动设置或通过交叉验证进行优化.本文参考以前的工作将h和hk参数值固定为0.5[16-17].

对于多任务TSK 模糊系统的后件参数学习，首先令

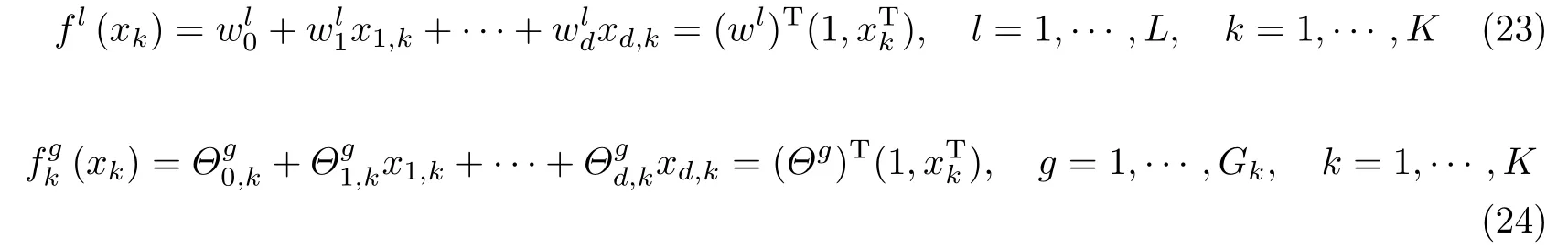
式中，fl(xk)为第l个公有模糊规则的后件输出；为第k个任务中第g个私有模糊规则的后件输出，wl为第l个公有模糊规则的后件参数；Θg为第k个任务中第g个私有模糊规则的后件参数.将式(23)和(24)代入式(12)可得

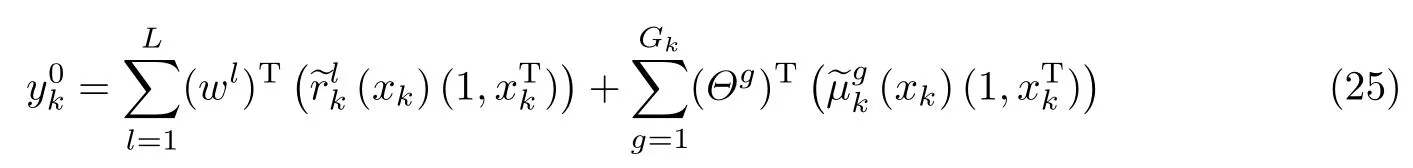
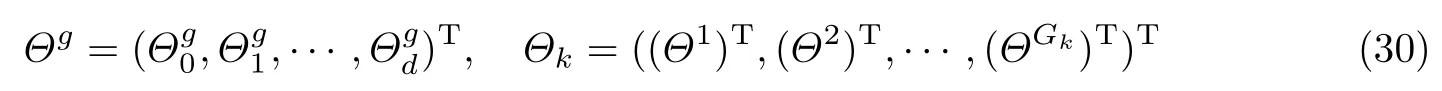
因此，上述多任务TSK 模型的训练问题可以转化为相应线性回归模型中参数的学习问题.参照文献[14,17,35]，本文基于经典的不敏感准则和L2 范数惩罚项设计了多任务TSK 模糊系统的后件优化目标函数

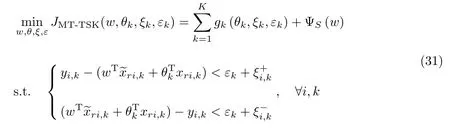
其中，

式(31)中第1 项用于学习任务k的私有后件参数θk，而式(33)则用于学习所有任务的公有后件参数w.值得注意的是，正则化参数τk >0 需手动设置，也可以通过交叉验证策略来确定[43].

为了获得最佳的后件参数w和θk，给出拉格朗日函数JMT-TSK(w,θk,ξk,εk)如下：

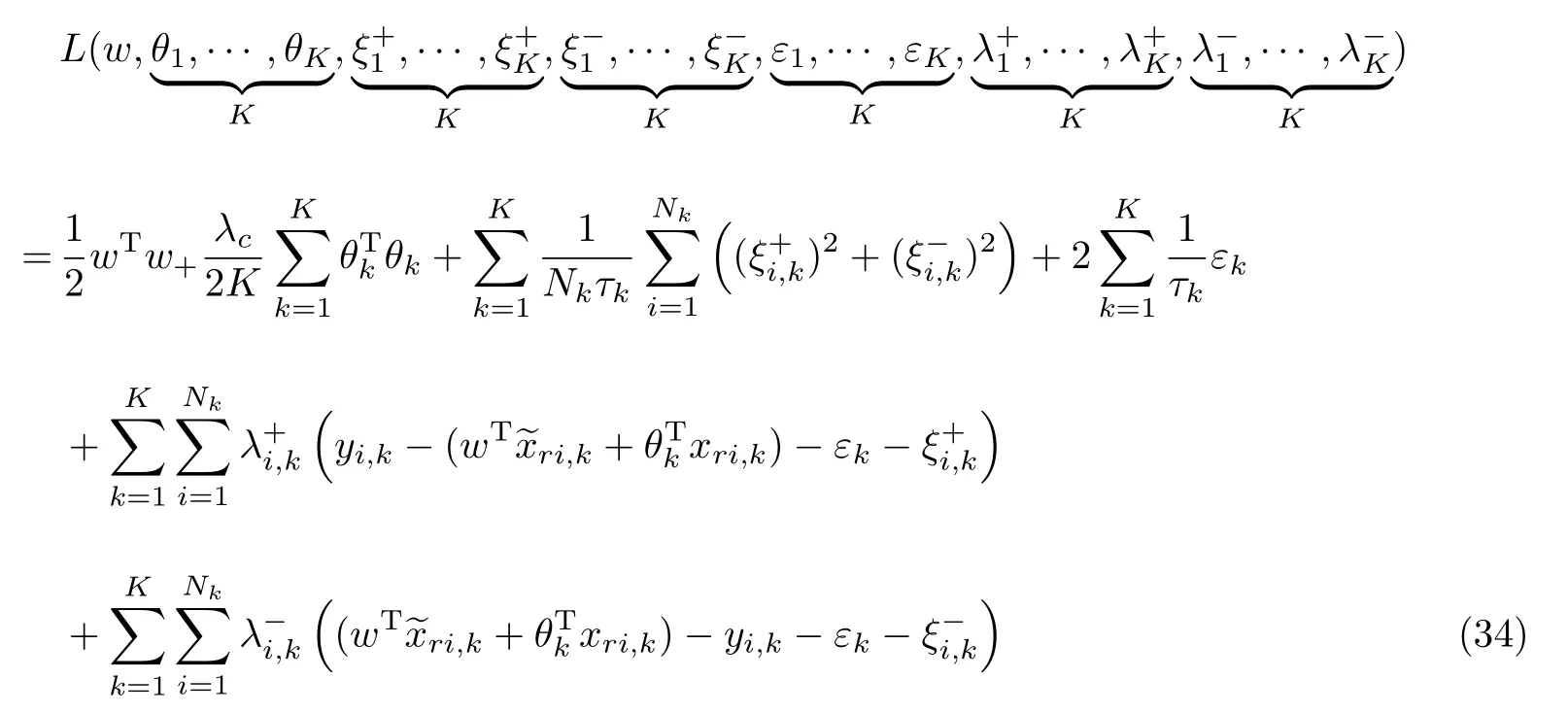
通过设置函数L(•)关于w,θk,,和εk的导数为0，可以获得

当将式(35)∼(39)代入式(34)时，则可获得其对偶问题

根据拉格朗日最优化理论，令

则式(31)可进一步表示为

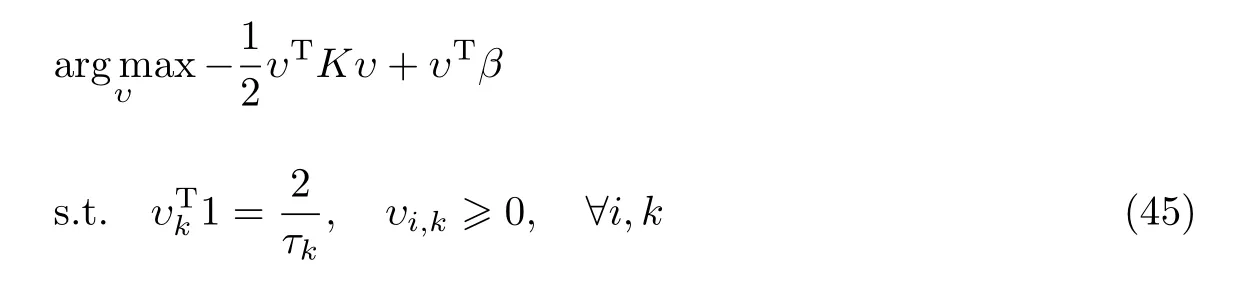
其中，

综上，MTFCM-MT-TSK-FS 的后件参数优化问题则转化成了一个典型的Quadratic Programming(QP)问题.本文使用传统的QP 算法[44]求解式(45)得到对偶的最优解公有后件参数和私有后件参数的计算式可以写为

基于上述推导，则所提的MTFCM-MT-TSK-FS 模型的学习算法可以描述如下：

算法MTFCM-MT-TSK-FS

步骤1设置每个任务的正则化参数τk和λ，公有模糊规则数L，私有模糊规则Gk.

步骤2使用多任务聚类算法MTFCM 根据输入数据x和输出y确定先行参数，并生成每个任务的公有回归数据集和私有回归数据集Dk={xri,k,yi,k}.

步骤3使用式(40)或式(45)输出拉格朗日乘子

步骤4根据步骤3，分别为所有任务和每个任务k获取最终的私有后件参数w和θk.

步骤5利用步骤2 的最终前件参数和步骤4 的后件参数，为每个任务生成所需的多任务TSK 模糊系统.

最后，我们来分析MTFCM-MT-TSK-FS 模糊系统的时间复杂度.MTFCM-MT-TSK-FS使用MTFCM 聚类得到规则前件，其时间复杂度是其中T是算法迭代的次数，是k个任务总的样本数目；是私有聚类数，P是公有聚类数.用多任务后件优化学习后件参数的时间复杂度是O(N3).因此，MTFCM-MT-TSK-FS的时间复杂度是

4 实 验

本节将评估由多任务模糊c 均值算法驱动的多任务TSK 模糊系统MTFCM-MT-TSK-FS模型的性能，并与3 种单任务TSK 模糊系统学习方法（L2-TSK-FS模型[35]、TSFS-SVR模型[36]、FS-FCSVM 模型[37]）及2 种多任务TSK 型模糊建模方法（MT-TSK-FS[16]和MTCSTSK-FS[17]）进行性能比较.为了进行公平地比较，本研究用4 组合成的多任务数据集和3 组真实的多任务数据集.

4.1 实验设置

4.1.1 实验环境

实验所使用的计算机的CPU 为Intel Core i5-3317U 1.70 GHz，RAM 为16GB，开发环境为MATLAB.

4.1.2 性能评估方法

泛化性能指标J[16-17,35]：其中N为测试数据集中的样本个数；yi为第i个测试数据的输出；y＇ 第i个测试数据的模糊模型输出，J值越小，泛化性能越好.

4.1.3 参数设置

1）对于L2-TSK-FS、TSFS-SVR、FS-FCSVM、MTCS-TSK-FS，采用与文献[17]相同的实验设置.

2）对于MTFCM-MT-TSK-FS 模型，采用以下实验设置：a）模糊规则数量：对于合成数据集，在参数集{5,10,15,20,25,30} 内设置单独的和通用的模糊规则的数量.对于真实数据集，根据数据集的规模，分别在参数集{5,10,15,20,25,30} 和{2,3,4,5,6,7,8,9,10,11,12,13,14,15} 内设置个体规则和公共模糊规则的数量.b）针对所提出的MTFCM 的设置，将模糊系数m设为2，阈值Θ设为0.95，MTFCM 中的λa，λb设置范围为{2−6,2−5,···,25,26}；c）MTFCM-MT-TSK-FS 的正则化参数τ和参数λc，它们的取值范围均为{2−6,2−5,···,25,26}.

4.2 合成数据实验结果与分析

4.2.1 合成数据集描述

为进行公平地比较，采用文献[17]中的4 种合成多任务数据集，这些数据集能够模拟不同的多任务场景，具体如表2所述.

表2 4 种合成数据的详细描述Table 2 Detailed descriptions and settings of four multi-task synthetic datasets

4.2.2 性能比较

本节采用5 种基于TSK 模型的相关模糊系统建模方法，对4 种不同的多任务数据集进行了比较研究.这些方法的相应结果示于表3和图2中.该实验设计了两个不同的比较方向：一是性能比较如表3所示，二是模糊规则数的比较如图2所示.通过对表3和图2的详细分析，可得到如下结论：

表3 不同模糊系统在合成数据集上的泛化性能Table 3 Generalization performance of different fuzzy systems on synthetic datasets

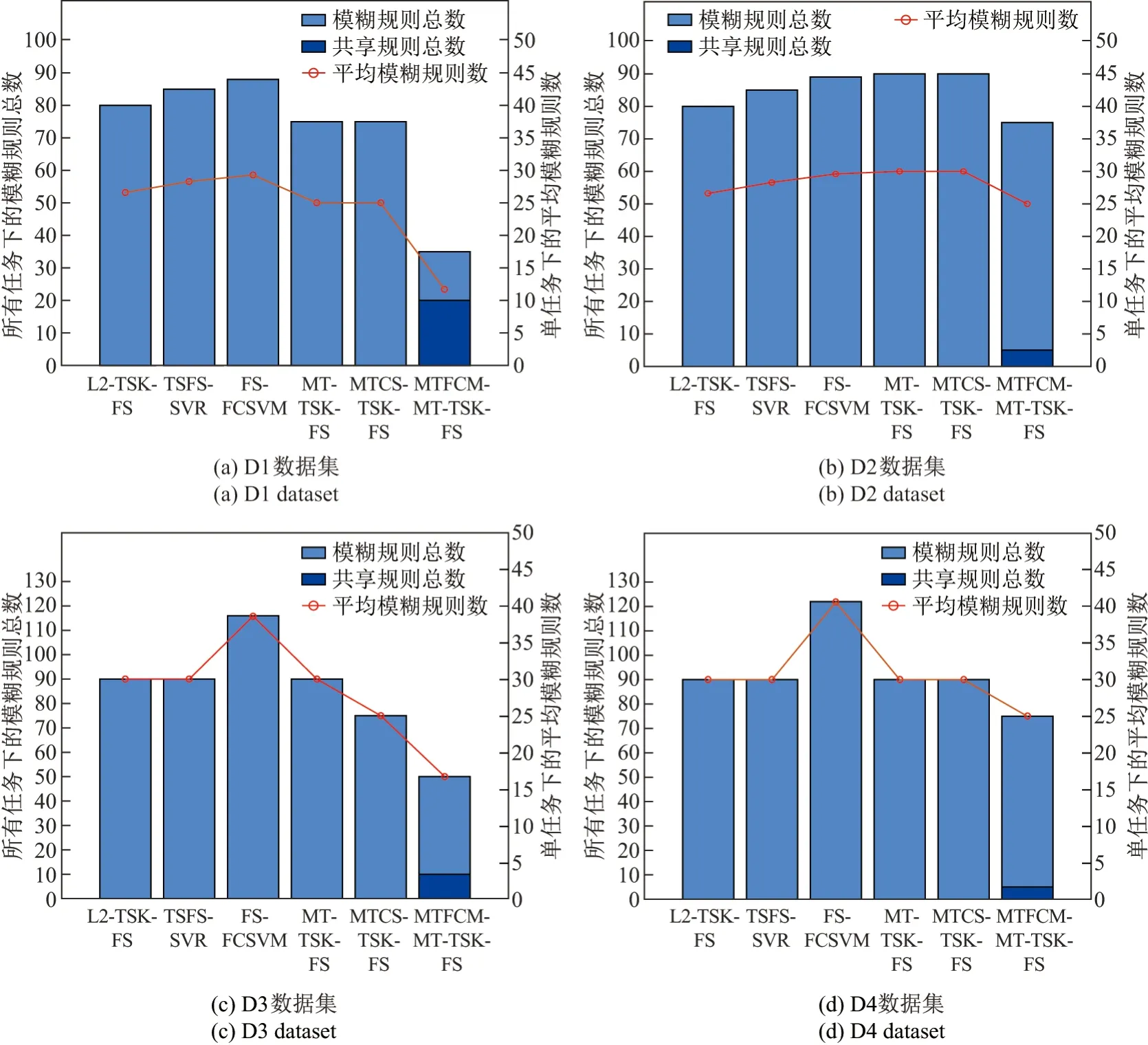
图2 各个模型在5 种合成数据集上得到的模糊规则数Figure 2 Numbers of fuzzy rules obtained by different methods on five synthetic datasets

1）在表3中，在不同的多任务场景中，MTFCM-MT-TSK-FS 的泛化性能明显优于L2-TSK-FS，TSFS-SVR 和FS-FCSVM 这3 种单任务TSK 模糊系统建模方法.结果表明，与3种单任务建模方法相比，所提出的MTFCM-MT-TSK-FS 模型可以有效地利用每个任务的私有信息和所有任务之间的公有信息，而单任务TSK 模糊系统建模方法仅可利用每个任务的私有信息.因此，提出的MTFCM-MT-TSK-FS 模型建模方法获得了较之其他3种方法更好的泛化性能.

2）通过与两种多任务TSK 模糊系统建模方法MT-TSK-FS 和MTCS-TSK-FS 比较，表3中的结果表明，所提的MTFCM-MT-TSK-FS 模型建模方法可以与现有的多任务模糊系统建模方法性能相当.结果进一步表明，所提出的用于学习前件参数的多任务模糊c 均值聚类方法和用于学习后件参数的多任务协同学习后件优化方法能够提升多任务TSK模糊系统的泛化性能.

3）图2中浅蓝色的柱子表示由各方法构成的模糊系统的规则总数，深蓝色的柱子表示公有模糊规则的数量.红线表示各方法构成的模糊系统的模糊规则的平均数.根据图2中的结果，MTFCM-MT-TSK-FS 比其他方法拥有更少的模糊规则，间接地说明本文提出的方法具有更好的可解释性和更简洁的模型结构.

4.3 真实数据实验结果与分析

4.3.1 真实数据描述

为了进一步评估所提出的MTFCM-MT-TSK-FS 方法在实际应用中的性能，本节给出了5 个真实多任务建模问题.这些数据集简要描述如下：1）谷氨酸发酵过程建模问题[16-18]；2）聚合物测试工厂建模问题[17]；3）葡萄酒偏好建模问题[16-17,45]；4）混凝土坍落度建模问题[17]；5）多值（MV）数据建模问题[17].

4.3.2 性能比较

表4给出了6 个模型在5 个真实多任务回归数据集上获得的实验结果.图3给出了各个方法在5 个真实数据集上的模糊规则数.实验结果与合成数据类似，结果进一步表明，所提的MTFCM-MT-TSK-FS 模型建模方法比单任务TSK 模糊系统建模方法具有更好的泛化性能.此外，图3也进一步说明了MTFCM-MT-TSK-FS 模型再保持泛化性能的同时具有更少的模糊规则数.总体而言，基于真实数据的应用结果表明，所提出的MTFCM-MT-TSK-FS 模型建模方法在泛化性能和可解释性两个方面均优于现有的单任务或多任务TSK 模糊系统[16-17].

表4 不同TSK 的模糊系统在真实多任务数据集上的泛化性能Table 4 Generalization performance of different TSK-based fuzzy systems on real-world multitask datasets

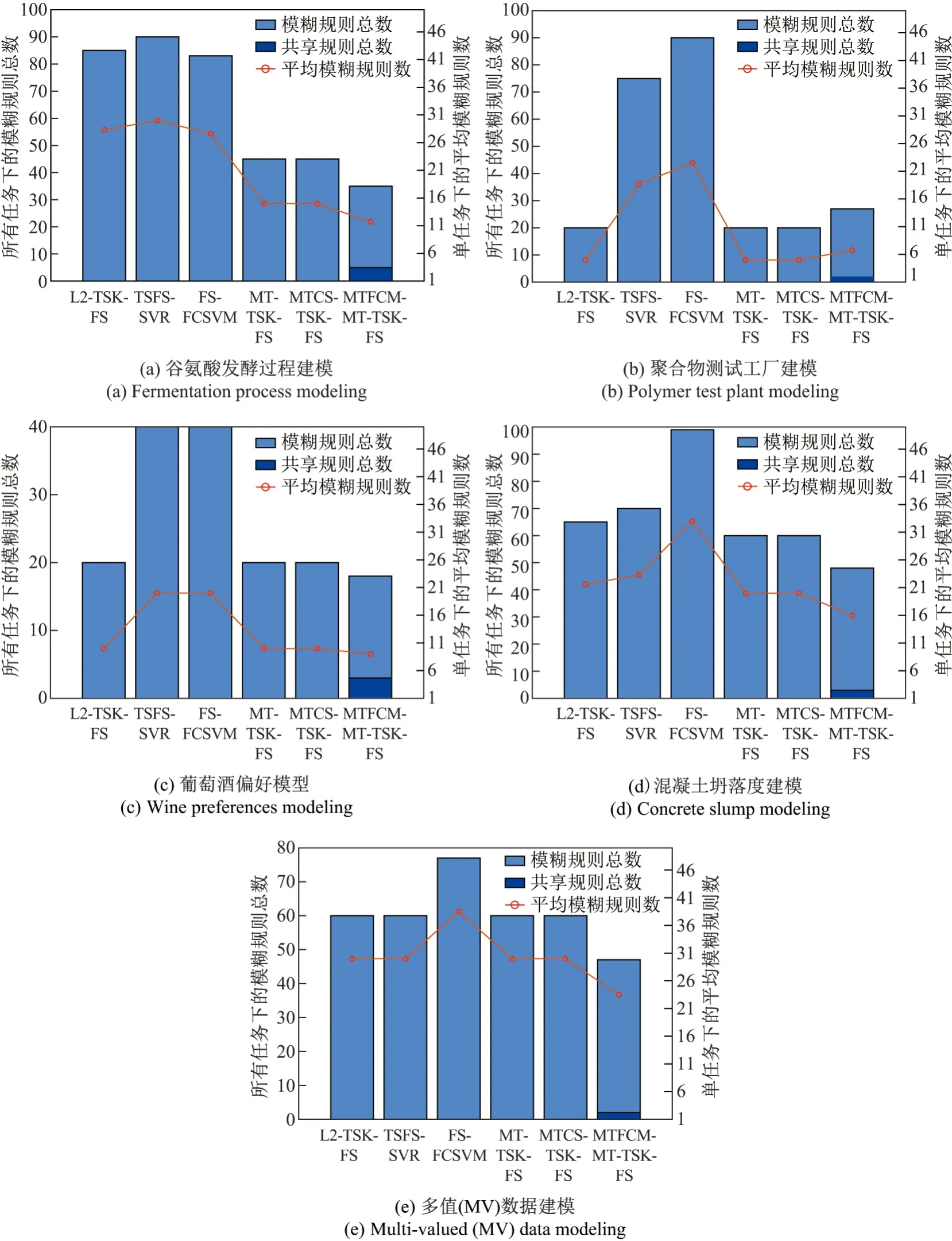
图3 各个方法在5 个真实数据集上的模糊规则数Figure 3 Numbers of fuzzy rules of different methods on five real-world datasets

5 结 语

本文旨在提出一种多任务聚类机制用于优化多任务TSK 模糊系统的前件参数，以及一种具备多任务协同学习能力的后件参数学习方法用于优化多任务TSK 模糊系统的后件参数.实验结果表明，所提出的MTFCM-MT-TSK-FS 模型建模方法在泛化性能和可解释性两个方面均优于现有的单任务或多任务TSK 模糊系统.尽管所提出的MTFCM-MT-TSK-FS 模型建模方法有诸多优势，但该模型仍有进一步研究的空间.具体地，MTFCM-MT-TSK-FS 模型建模方法拥有多个需人工预设的参数，如模糊指标和正则化参数，这将导致获取模型最优性能的计算代价过高.在本研究中，我们使用五重交叉验证的策略来确定这些预设参数，这需要耗费大量的时间成本.理论上，进化学习技术可以解决这一问题.然而，使用这些技术进行参数调优也面临一些挑战，如计算复杂度高、随机性强.今后我们将在此问题上开展更深入的研究工作.