基于逻辑回归算法的校园一卡通数据挖掘与应用

陈云川,宋 浩,赵 烨,刘发稳

(昆明冶金高等专科学校计算机信息学院,云南 昆明 650033)

0 引 言

随着校园一卡通系统的不断完善，学生不仅可以用一卡通食堂就餐，还可以在校内进行各种类别的消费与活动：超市购物、洗衣、洗澡、借阅图书、进出教室、进出宿舍、点名签到、查阅个人成绩——一卡通有了越来越多的使用场景。一卡通系统的不断升级完善，使校园管理日趋智能化和高效化。收集学生的一卡通刷卡记录[1]，从这些海量的数据中分析出一些“有用信息”，可以帮助学校更好地为学生服务。本文将数据挖掘技术应用于学生一卡通数据的分析，借助Rapidminer平台，采用逻辑回归算法构建训练数据集模型。模型不断被修调优化后，将用于预测分析测试数据集[2]，挖掘分析一卡通数据，精准识别品学兼优但家境贫寒的学生并提供帮助。

1 数据挖掘分析流程

数据挖掘技术可以从海量的数据中，通过建立相关的分析模型，找出数据中蕴藏的“有用信息”，对现实中的某个事物进行解释，或者对某个目标进行预测。一般数据挖掘需要经过如下几个步骤[3]：

1)数据获取与目标确定。在数据挖掘分析之前需要得到建模所需的原始数据集，并明确本次挖掘分析的目标。

2)数据清洗与属性规约。由于原始数据集中有很多缺失数据和噪声数据，会导致模型不稳定且准确度下降，这样的数据集是不满足挖掘建模条件的。所以在正式建模之前，需要先对数据集进行清洗:可以采用过滤的方式也可以采用中值填充或者特定值填充的方式处理缺失数据;而对于噪声数据，则需要结合具体的挖掘需求与数据集特征，认真分析它们出现的原因，并谨慎处理。若原始数据属性值太多，会加大直接建模难度，且模型的准确度不高。这个时候需要进行属性规约，根据挖掘任务及数据集内部结构特点，对数据集进行属性约减，一般采用主成分分析法和关联分析方法，观察各属性值与目标属性值之间的关系，将重要的属性筛选出来；最后根据挖掘模型对数据格式的要求，对原始数据按照模型要求进行归一化处理——这样就得到了挖掘建模所需的训练数据集。

3)挖掘建模。根据挖掘目标及训练数据集情况，选择合适的算法建模。根据任务，挖掘模型一般分为：分类、估计、预测、关联、聚类5种。分类模型可以将数据集按照需要，分为若干个类别；估计与预测模型可以为用户预测某一属性值并给出可能的相关概率；关联模型主要用来寻找多个属性变量之间取值的规律性和相关性；聚类和分类很像，但是聚类的簇不是事先人为设定的，而是根据数据集本身的内部结构和关系，主要依赖相似度计算来实现簇的划分。在选择算法进行建模时，一定要明确挖掘的目标和功能需求，然后用训练数据集构建模型，并进行多次修调。

4)模型应用。将训练集建模得到的挖掘模型，应用于测试集的分析预测。这个过程可以进一步检验和评估挖掘模型，判断预测分析结果是否符合最终的需求，并进一步评估模型的性能。

2 建模采用的挖掘分析算法——逻辑回归算法

用函数表达式拟合数据集的方法有很多，应用比较广的是线性回归算法与逻辑回归算法。线性回归算法主要是对属性的数值进行预测，而逻辑回归算法主要是用于属性的分类问题。逻辑回归算法属于典型的分类算法，类似于决策树算法或贝叶斯算法[4]。

线性回归模型，是通过寻找一个函数表达式f(x)，使数据点尽可能多地落在f(x)确定的图像上。表达式中，自变量x与因变量y之间是满足线性关系的，即随着x的变化y呈线性变化，并且训练得到的线性回归模型可以对新数据点进行属性值的预测[5]。在线性回归模型中，不论是自变量还是因变量都是连续型数据。线性回归图像如图1所示，随着自变量x的增加，因变量y也会增加。

图1 线性回归图像Fig.1 Linear regression image

当面临的数据是离散型数据时，采用线性回归拟合数据如图2所示：虽然自变量的值是连续的可以取任意数值，但是因变量值只有2个。自变量与因变量之间的关系不像线性回归模型那样是渐进式的，因变量y的取值有了跳变[6]。这时，如果还是采用线性回归的方式用一条直线来拟合数据集，那么绝大部分的数据点并不能落在这条直线上，这样一来训练得到的模型准确度就非常低了。为了解决这个问题，可以采用S型曲线对数据点进行拟合，采用逻辑回归拟合数据如图3所示，这样数据集中的绝大部分点就落在了这条S型曲线上了，这时只需要寻找到这条曲线的函数表达式，那么这个函数就能描述数据集了。逻辑回归算法就是用来解决离散型数据问题的。

图2 线性回归拟合数据

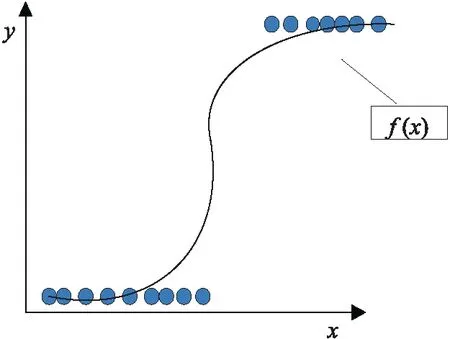
图3 逻辑回归拟合数据

在逻辑回归模型中，因变量是一个二元型的数据，即因变量只有2种取值——是或否、通过或不通过等。建立逻辑回归的目的是找到一个函数，将二元型因变量y和自变量x联系起来。在线性回归模型中，以一元线性回归为例，要找到一条直线拟合所给数据集，那么只要找到准确的斜率b1和截距b0这条直线就确定了。在逻辑回归中，需要找到的是曲线方程，用来描述因变量y与自变量x之间的关系。

其实，只要将因变量y出现的概率值取对数，得到新的因变量，那么这个新因变量和自变量x之间就是线性相关的。此时的新因变量y表示y=1或者y=0时的概率。详细过程如下。

1)逻辑回归模型中y为某一事件，是一个二元型数据，即y的取值是：通过或不通过，回应或拒绝、出现或不出现；

2)当y=1时，认为事件发生，概率为p；

3)当y=0时，认为事件不发生，概率为1-p；

4)那么该事件发生的概率就是p/1-p；

5)将p/1-p取对数，得到的新因变量log(p/1-p)，是与自变量x线性相关的，这个概率对数函数就称为logit函数，他们之间满足如下线性关系：

(1)

当数据集包含多个属性时则为：

(2)

通过式(3)，可以得到p的求解方式：

(3)

根据所给数据集，结合公式(3)(4)，可以比较方便地计算出p值。为了实现这一目标，需要事先假定一组参数b1，b2，b3，…，b0。读入一个训练样本，先计算下列表达式：

py·(1-p)(1-y)

(4)

式(4)中，y表示实际数据集中的具体数值;p可以根据式(3)求出。假设某个数据点的实际y=0，但是根据逻辑回归模型预测的y=1且概率是0.9，即模型预测错误，那么根据式(4)，计算值= 0.1。当逻辑回归模型预测出的y值准确，但是概率很小比如0.1，那么根据式(4)，计算值=0.9。式(4)是似然函数的一种形式，当模型对某个数据集的预测结果越正确，所求得的似然函数值越大;当模型对某个数据集的预测结果越错误，所求得的似然函数值越小;当数据集中所有点的似然函数值相加，如果和越大意味着模型训练的准确度越高，反之亦然。

3 仿真实验验证

3.1 实验环境、平台、数据集描述

本文的实验环境为：Win7 64位系统，8G RAM，intel Core i7 cpu。实验平台是：Rapidminer Studio 6.0。实验数据集为网上开源的一卡通实验数据，包含 7 000 条一卡通原始数据，每条数据有25个属性，包含每个学生的食堂消费记录、图书借阅记录、学习成绩、进出宿舍记录等信息。特别说明：本文实验仿真中会多次提到算子，在Rapidminer Studio 6.0平台中是完成特定功能的函数。这些算子是使用JAVA语言编写的功能模块，可以完成数据转换、数据过滤、交叉验证、数据读写等功能。

3.2 逻辑回归模型仿真实验

为了应用逻辑回归算法对pingkunsheng标签属性值进行预测，需要进行以下几个步骤：

1)通过对训练集的数据进行分析清洗、属性规约，从而构建逻辑回归模型；

2)评估构建的逻辑回归模型性能；

3)对逻辑回归模型的相关参数进行修调；

4)将得到的逻辑回归模型应用于测试集上，从而预测测试集数据的标签属性值。

逻辑回归模型详细仿真流程如图4所示。

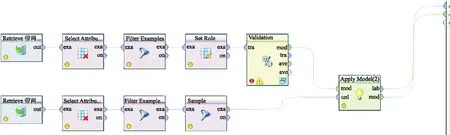
图4 逻辑回归模型详细仿真流程Fig.4 Detailed simulation flow of logical regression model

详细仿真流程介绍如下：

1)采用import csv file算子，导入原始数据集。

2)采用select attributes 算子，进行属性约减，约去消费方式和图书借阅时所在图书馆的序号等属性，留下建模用的16个属性。

3)缺失值过滤。由于在原始数据中，每一个属性下都有很多空白数据，会影响模型的生成。如果用均值或者某一个特定值填充这些空白数据，会造成模型的失真。所以对于含有缺失值的数据条目采取缺失值过滤的方式进行，最终得到 6 305 条数据。

4)引入set role角色设置算子，将pingkunsheng改为标签属性。

图5 逻辑回归模型AUC与ROC曲线 Fig.5 Logical regression model AUC and ROC curve

5)split validation划分验证算子是一个带有嵌套功能的算子，双击split validation算子可以进入嵌套设置界面。这个界面由左右2个窗口组成，在左边模型训练窗口添加logistic regression 逻辑回归算子，在右侧模型测试窗口添加apply model模型应用算子与performance模型性能表现算子，点击performance算子，勾选accuracy(准确率)、AUC、precision、recall这几个参数。

6)训练集建模结果：逻辑回归模型准确率、模型精度、模型召回率如表1所示，逻辑回归模型AUC与ROC曲线如图5所示。

7)测试集结果验证。为了保证测试数据属性个数、属性取值范围等与建模数据一致，测试数据也经过了与建模数据一致的数据清洗过程：属性约减与缺失值过滤的条件都一致，测试集中属性约减多删除pingkunsheng一项，因为这项属性是要预测的；然后选取其中的100个数据进行模型验证。sample算子：从清洗后的测试数据中选出100个来进行试验。apply model算子：将逻辑回归模型应用于测试集上，来预测测试集所属的类别，最终测试集标签属性被成功预测，而且每一条数据的标签后都有模型预测的相关概率值，逻辑回归模型性能如表1所示。

表1 逻辑回归模型与贝叶斯模型性能比较Tab.1 Performance comparion between logical regression model and Bayes model

8)对比试验。将建模算法改为经典的贝叶斯算法进行对比试验，对训练集数据的预处理和之前逻辑回归模型基本一致，也是经过了缺失数据的过滤和噪音数据的清洗，并根据主成分分析法进行了属性的规约，在split validation算子中选择贝叶斯算子，参数设置选择默认方式，仿真结果(贝叶斯模型准确率、模型精度、模型召回率如表1所示)，模型AUC与ROC曲线如图6所示。

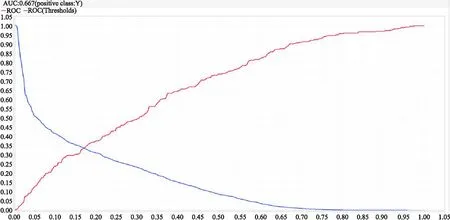
图6 贝叶斯模型AUC与ROC曲线Fig.6 AUC and ROC curves of Bayes model

逻辑回归算法实验结论：逻辑回归算法属于数据挖掘分类算法中的一种，作用是对标签属性值进行预测，从而实现数据集的分类。本次试验为了进行试验结果的对比验证，在仿真时引入了经典的贝叶斯算法。用逻辑回归算法和贝叶斯算法进行训练集建模，原始数据的处理都经过了属性约减、缺失值过滤和噪声数据清洗，最终得到如下结果：逻辑回归算法在准确度、精度、RUC值方面要优于贝叶斯算法，但是在召回率方面比贝叶斯算法要弱一些；将训练集建模得到的逻辑回归模型应用于测试集数据,可以成功预测标签属性pingkunsheng，而且每一条预测出的标签属性还提供了置信度这一指标。

4 结 语

校园一卡通建设是“智慧校园”的重要一环，一卡通中包含有食堂消费记录、图书借阅记录、超市消费记录、进出校园记录等数据。对这些数据进行数据挖掘和分析，可以得到一些“有用信息”，用以评估学生的生活方式、作息规律、消费情况、学习状况等，帮助学校更好地服务学生。本文提出挖掘一卡通数据、分析从而找出符合助学金认定的学生，只是理论层面的尝试和应用，在实际情况中还需要多方面多角度进行综合评判；接下来在对一卡通数据进行建模分析时，还需要引入聚类算法、关联算法等机器学习理论，在建模时采用交叉验证等集成建模方式进一步完善和改进分析预测模型。