一种欠驱动3D打印机械手的结构设计
赵英涛,Kevin Montes Dorrego,李 亚,毕德学
(天津市轻工与食品工程机械装备集成设计与在线监控重点实验室,天津科技大学机械工程学院,天津 300222)
近些年来,机器人技术快速发展,机器人被广泛应用于诸多领域,代替人类完成比较危险的任务.末端执行器是机器人去完成各种工作的关键执行部分.理想的末端执行器应该具有结构简单、易于控制[1-3]、通用性强等特点,能够抓取多类物体.国内外已有各种类型的机械手,例如,早期日本的 KONDO机械手[4]和 NASA开发的 Robonaud机械手,在国内有清华大学设计的拟人机械手TH-3B[5]以及赵思宇[6]设计的欠驱动机械手.本文采用欠驱动原理设计出一种结构简单、通用性更强的机械手.此欠驱动机械手采用 3D打印技术制作,不但能实现稳定抓取工件的功能,而且制作成本低、易修复且质量小,能满足UR5机器人对手臂质量限制的要求.
1 欠驱动机械手的机械设计
1.1 欠驱动原理及特点
欠驱动是相对于全驱动而言的,欠驱动是指驱动器数目少于本身自由度数目,而全驱动是指在正常工作条件下机构自由度的数目与驱动器数目相同[7].多指机械手的手指通常有很多关节,全驱动方式意味着每个关节都必须加装驱动器;而欠驱动方式下,通常只需要很少的驱动器驱动,依靠弹簧、限位装置等结构正常工作.如,一个两关节欠驱动手指的工作原理如图1所示[8-9].
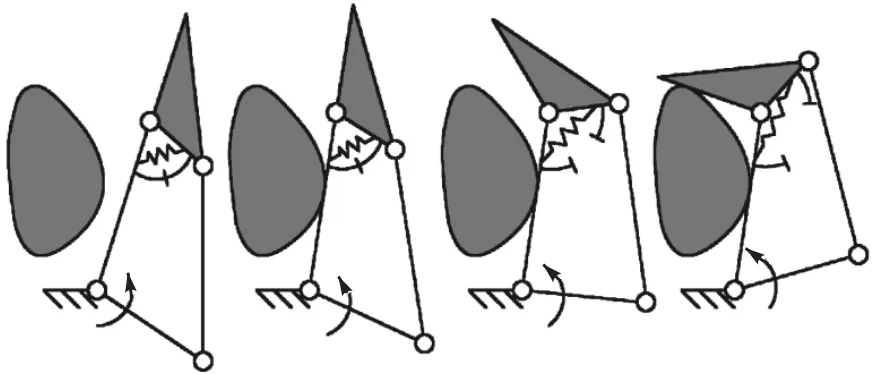
图1 两关节欠驱动手指工作原理Fig. 1 Working principle of underactuated fingers with two joints
1.2 欠驱动机械手机构设计
欠驱动3D打印机械手的总体设计示意图如图2所示.
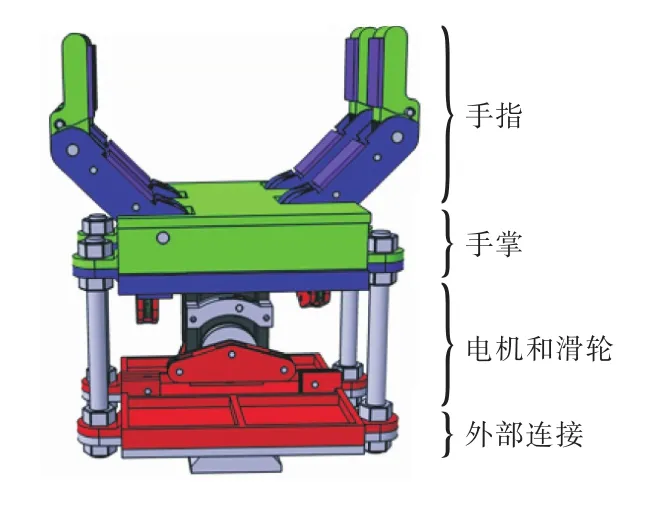
图2 机械手的总体设计示意图Fig. 2 Overall design of the hand
1.2.1 手指及手掌设计
机械手共有 4根手指,每根手指有两个关节.每根手指在闭合运动中有两个欠驱动自由度,利用肌腱和一个具有扭转作用的弹簧实现开启运动.手指被设计成一个紧凑和坚固的结构,以便更好地将肌腱和扭转弹簧安装在它的内部,如图3所示在手指关节处设计了开合角度的限制,可简化手指结构.
手掌连接手指和驱动系统,同时它还容纳部分滑轮系统.它由两部分组成:一是如图 4(a)所示的上盖为手指固定的位置,它的作用就像人的手掌是抓握物体时的接触点.它也是手指的近端旋转极限和扭转弹簧的固定点.二是如图4(b),蓝色盖板上有固定滑轮和电机的位置.它们通过4个M8的螺母与螺栓连接固定在一起,并与机械手的其他部分一起固定.

图3 手指设计Fig. 3 Finger design
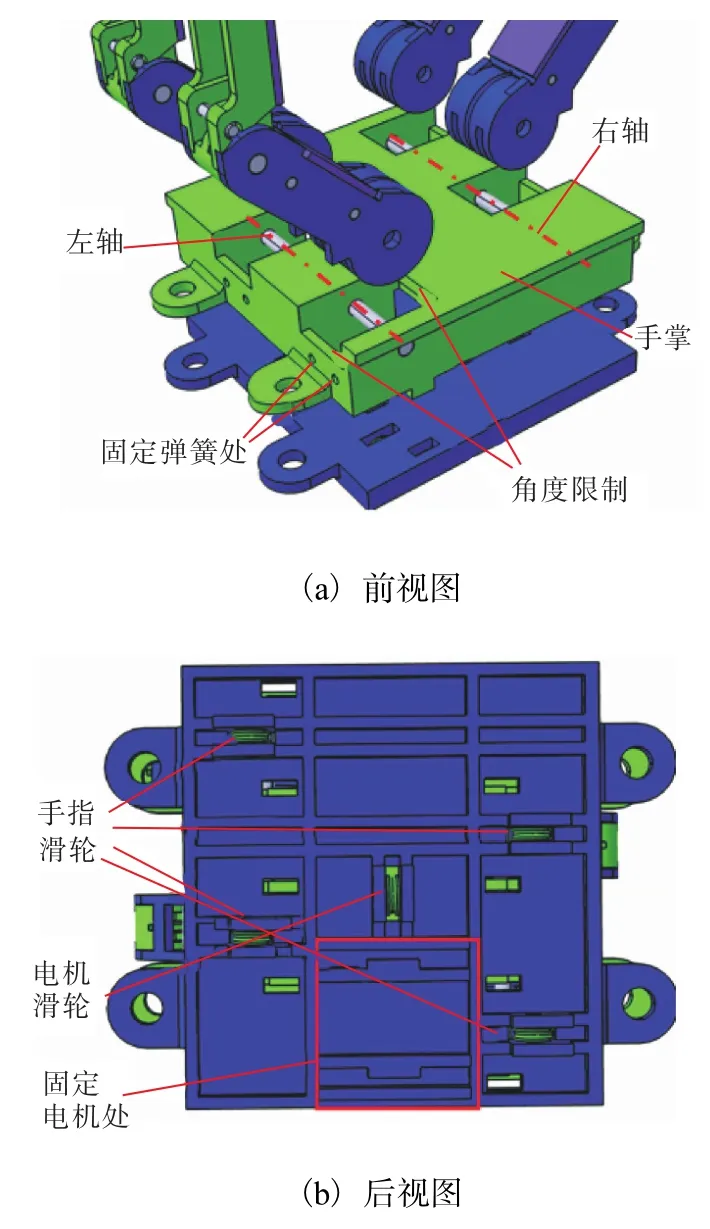
图4 手掌设计Fig. 4 Palm design
1.2.2 滑轮系统设计
图 5是差动滑轮系统实现欠驱动的示意图.伺服电机带动曲柄转动,曲柄拉动缆线.由缆线传递的力被滑轮差速器 1平分成两个相等的力.这些缆线所传递的力又被另外两个滑轮差速器2和3平分,所以 4条缆线上的拉力是相同的.每根缆线都能控制一根手指,这样所有的手指都能获得相同的扭矩.4条缆线输出的张力是相同的,但当左侧缆线位移受到限制时,动滑轮1会自适应平衡位置使右侧缆线位移不受限制,每个输出缆线可移动不同距离.
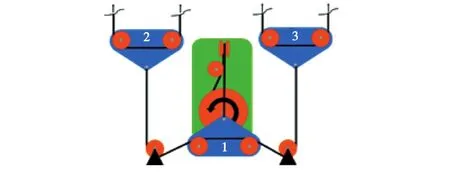
图5 手指间欠驱动系统图Fig. 5 Underactuated system diagram between fingers
当电机扭矩均匀分布在4根肌腱上,这些肌腱便开始控制手指移动,如图 6所示.每个指骨的入口滑轮半径(r2)决定了它传递的扭矩大小.
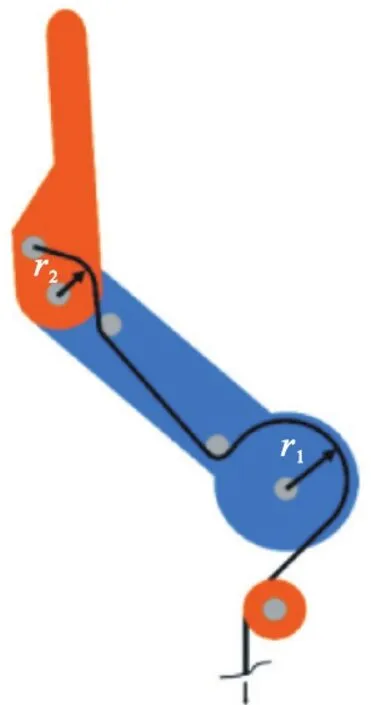
图6 手指上肌腱布线图Fig. 6 Routing map of superior tendon of a finger
1.2.3 底部盖设计
底部盖有两个作用,固定电机位置和连接滑轮系统底部,它附在机械手底座上,如图 7所示.机械手底座有两个部分,分别为具有位置调节功能的燕尾槽和连接法兰.
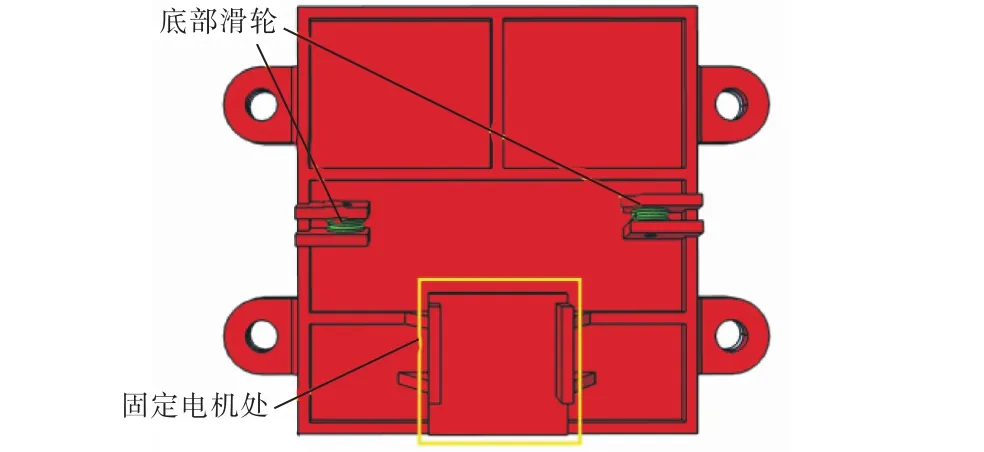
图7 底部盖设计Fig. 7 Bottom cover design
2 抓握类型分析与参数设计
2.1 抓握类型分析
机械手闭合及打开的动作与人手闭合及打开的动作相似.这意味着首先要关闭近端指骨,直到都完全接触到物体,远端指骨才开始进行闭合.开口运动是逆序的,首先打开远端指骨,然后再打开近端指骨.欠驱动也产生自定心作用,如图 8所示.这就减少了对机械手精确定位来抓住物体的必要性.对于不规则形状的物体,根据前面解释的顺序,机械手闭合会自动将物体集中到手中心并闭合指骨.在如图 9所示的平衡位置之前,由于差动作用,每个手指的位置都不同.

图8 抓取物体的自定心Fig. 8 Self-centering in grabbing objects

图9 手指对不规则物体的自动适应Fig. 9 Automatic adaptation of fingers to irregular objects
为了分析抓握类型,将考虑使用双指手和圆柱形工件.一个四指机械手的接触数将是图 8和图 9列出类型的两倍.5点抓握:在这种情况下,所有的指骨和手掌都与物体接触.由于接触点的数量最多,它是最稳定的握法.它限制了物体被挤压到手掌的力,当近端指骨失去接触,可变为 3点抓握.4点抓握:物体接触所有指骨,但不接触手掌.但如果一个物体受到垂直于手掌的力,它便不具有很好的抓握稳定性.3点抓握:物体接触手掌和远端指骨.这种抓握类型允许以最大的力将物体推到手掌上.但同时要求远端指骨必须足够长.2点抓握:用远端指骨抓住物体的类型.这种抓握类型抓取不稳定,一般不建议采用这种方法.
2.2 设计参数
四指机械手投影到平面上的各尺寸如图 10所示.本文将研究由两个手指组成的欠驱动机械手,但尺寸设计和驱动参数可直接适用于四指机械手.设计参数:手掌宽度的一半 L0、近端指骨的长度 L1、远端指骨的长度 L2以及关节和接触面处的手掌和指骨厚度 t.唯一的驱动参数是传动比 R,传动比是指远端指骨转矩T2与近端指骨转矩T1的比值.参考对象为圆,其半径为 robj.假定初始指骨是直的,近端指骨的最小和最大旋转角为 θ1o、θ1c,远端指骨最小和最大旋转角 θ2o、θ2c.包住物体意味着手指包住物体周长的一半以上.
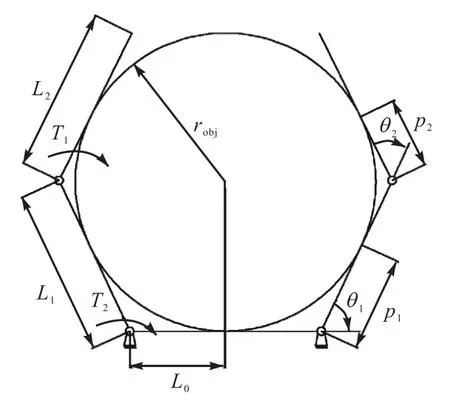
图10 机械手的尺寸参数Fig. 10 Dimensional parameters of the hand
2.2.1 几何方程边界条件
为了确定所抓握物体的最大和最小尺寸,用闭环方程来确定与指骨的接触点.近端指骨的接触点与关节的距离p1和近端指骨的旋转角度θ1可以通过式(1)确定.

其中 0<p1<L1,Yobj是物体中心和手掌之间的距离Yobj≥ robj+t ,假设Xobj关于Xobj=0的直线对称.远端指骨的接触点与关节的距离p2和远端指骨的旋转角度θ2可以通过式(2)计算.
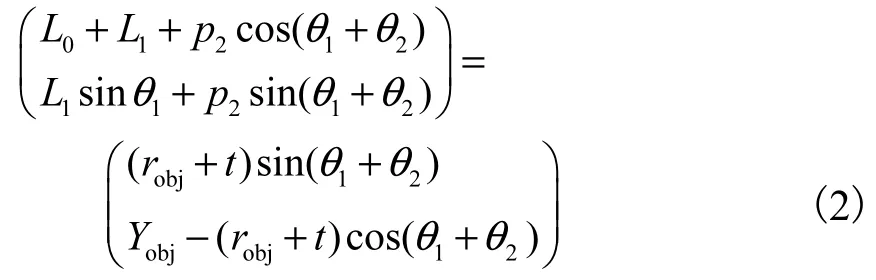
其中0<p2<L2.
5点抓握:须满足式(1)、式(2)和 Yobj=robj+t.对于圆柱形物体接触点几何条件为 p1=L0和p2= L1-L0.说明当 L0≤ L1≤ L0+L2时,此情况发生.要包住一个物体,指骨的旋转角度满足:θ1+θ2≥ π /2.θ1和 θ2可以由余弦规则求得.

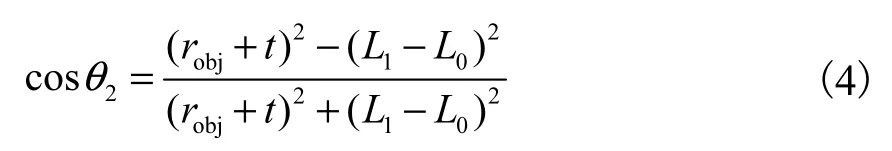
将式(3)和θ1+θ2≥ π /2 代入式(2),求得 5点抓握物体的robj
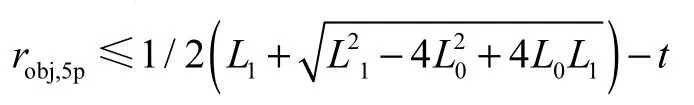
4点抓握:须满足式(1)、(2)和 Yobj> robj+t.此情况的发生取决于物体的大小和所在位置.接触点服从 p1> L0和 p2= L1-p1.说明当 L0< L1时,此情况发生.显然最小物体尺寸大于手掌宽度 robj,4p> L0.将p2=L1-p1和θ1+θ2= π /2代入式(1)和式(2)求最大物体尺寸:用笛卡尔公式得

3点抓握:当 Yobj=robj+t时,才满足指骨的闭环方程式(2).与 5点抓握相比,近端指骨的旋转角度更小.只有 L1≤L0+L2这种情况成立.将 Yobj=robj+t和θ1+θ2= π /2代入式(2)可获得 3点抓握的最大物体尺寸.当抓住最大的物体时,接触点在指尖.
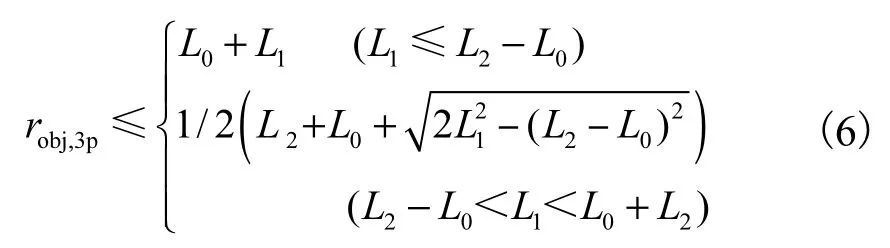
2点抓握:不适合2点抓取,故不研究.
2.2.2 驱动参数边界条件
现在,在物体和指骨中实现静态平衡的可能性还没确定.它取决于抓握的类型和传动比R.

为达到抓握平衡,指骨必须对物体施加力.如图11是对指骨和抓握物体间受力的分析,得
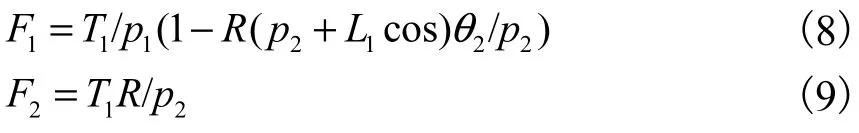
因为对称是假设的,所以必须只考虑合成的 Y方向力.对于5点和3点抓握,手掌的受力是正的.4点抓握手掌受力Fplam=0.当近端指骨没有使力,即1F=0时1

F=0的条件:
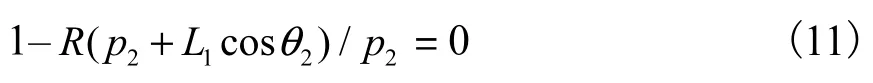
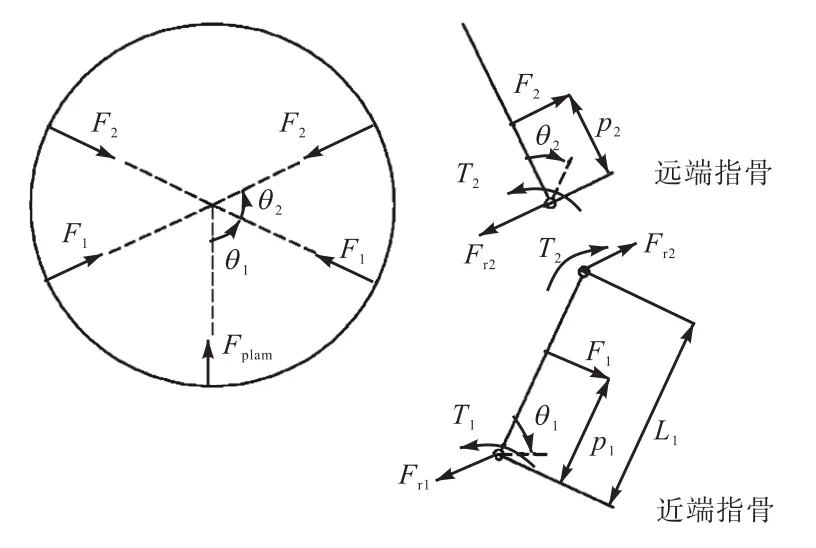
图11 指骨和物体受力分析Fig. 11 Force analysis of phalanges and objects
因机械手平衡和接触点数取决于R.故需确定各接触类型R的上下限.
5点抓握:当近端指骨失去接触(过渡到 3点抓握)时,R的上限达到.利用闭环方程,Yobj=robj+t和F1=0,解得rmax,5p
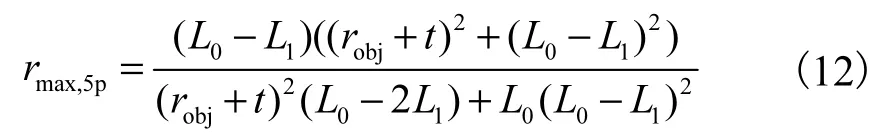
若式(11)要成立,则


4点抓握:当R为rmin,4p时,减小R将使物体远离掌心,从而导致物体从机械手弹出.反之,增大 R将使物体与手掌接触,直到过渡到 5点抓握.当 R=rmax,4p,根据 L2的大小,当 Yobj=robj物体接触手掌或当 p2=L2接触点在远端指骨的顶端.当 L1≤L0+L2时,抓握类型是从 4点抓握转换为 5点抓握,rmax,4p=rmin,5p.
rmin,4p受机械手开启物体弹射的限制.它须满足闭环方程,平衡方程(10),θ1+θ2≥π / 2,Yobj< robj+t和Fpalm=0,解得rmin,4p
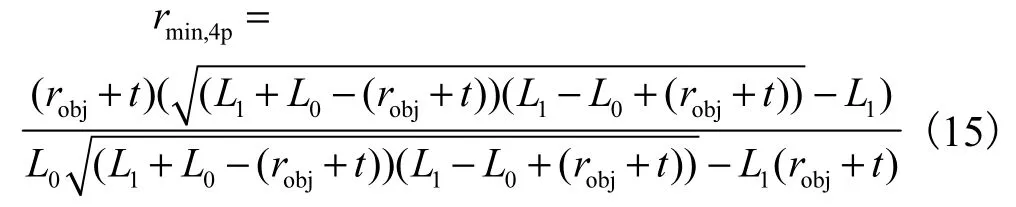
3点抓握:增大R导致远端指骨的接触点靠近手指顶端,而θ1将变小.当远端指骨的接触点超过其物理极限时,rmax,3p受机械手关闭物体弹出的限制.须满足以下条件:
远端指骨的闭环方程 p2=L2,F1= 0 ,Yobj=robj+t和Fpalm>0,解得
3点抓取的rmin,3p为向 5点抓取的过渡,所以rmin,3p= rmax,5p.
2.3 主尺寸和驱动参数
使用 2.2节的方法,以确保机械手能够实现对规定范围对象的稳定抓握.使用 3点、4点或 5点抓握,机械手必须能够成功地抓握直径为 25~100mm的物体,但最好是用 5点抓握.手指长度必须小于等于 100mm.由于制作精度原因,连接关节的直线处的手指宽度为 9mm.为了确保能够抓住直径为100mm 的物体,将增加 7.5%的加工余量.因此,设计对象的最大直径为107.5mm.
2.3.1 几何约束
要抓住圆柱,需满足 L1> L0和 L2> L1- L0.物体半径必须小于
由式(17)得当 L0=L1/2时,所抓握物体的尺寸是最大的.由 robj,max=53.75mm 和 t=9mm 可知:L1≥ 5 2mm ,L0=L1/2,L2> L1/2.
2.3.2 传动比R的约束
选择合适的传动比,机械手能拥有最大的抓取力,并对所抓取的物体具有抓握的稳定性.小伺服电机(扭矩为 7.3N·m)产生的转矩和肌腱传递这种力的能力是有限的,所以需要足够的力来抓住物体,这个力要尽可能高于给定的肌腱张力.
图12显示了不同尺寸的机械手、传动比R的接触点数是如何变化的.
图12 不同传动比(R)和机械手尺寸(L1,L2=100-L1和L0=L1/2)的接触点数Fig. 12 Contact points of different transmission ratio(R)and hand size(L1,L2=100-L1 and L0=L1/2)
在这些图形中有 5个不同的区域:在蓝色的线上,机械手闭合物体弹出;在蓝色和橙色线之间有一个 3点抓握类型;在被橙色和黄色线分隔的区域内,会出现一个5点的抓握;黄色线和紫色线之间的区域是4点抓握,在紫色线下面的区域可能会出现机械手闭合时物体弹出的现象.R小于 0的情况不可能出现.L1在 52~66mm 之间,因为它必须满足p2=L1-L0和θ1+θ2≥ π /2,手指总长度小于等于100mm.
当 T1为 1N·m、robj为 50mm 时,机械手尺寸对接触力的影响如图 13所示.抓握力被定义为物体在平衡位置上所有接触力的总和.可以看出,当 L1=66mm 时,抓握力最大.但是,误差不超过 8%,对于较小的物体,较短的近端指骨更方便.还必须考虑,如果近端指骨较长,则当机械手闭合时物体会弹出.因此,较短的近端指骨和较长的远端指骨具有更多的优势,保持力损失仅为 8%.故选择:L0= 2 6mm,L1=52mm,L2=48mm,R=0.5.
图 14为 T1=1N·m 时物体半径对接触力的影响,可以看出较小的物体所受的力较大.这张图也显示了抓握类型.图 14数据结果表明,半径小于48mm的物体有5个接触点.
图 13 T1=1N·m、robj=50mm 时,机械手尺寸 L1对接触力的影响Fig. 13 Influence of hand size L1 on contact force when T1=1N·m and robj=50mm
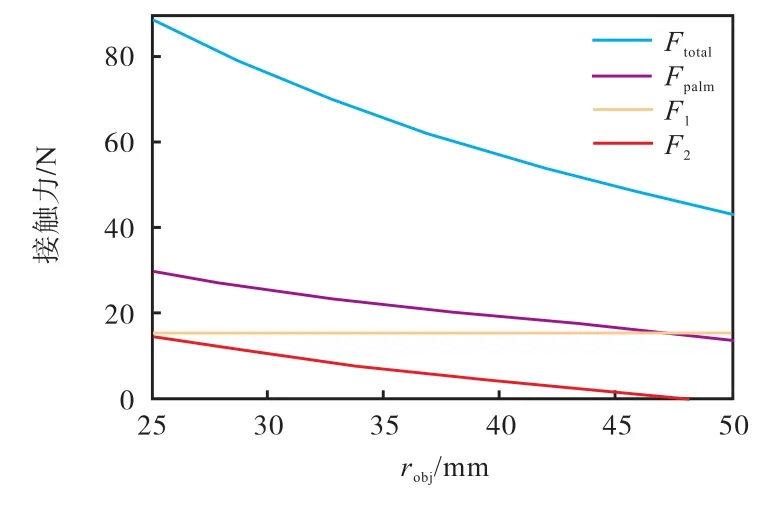
图14 T1=1N·m时物体半径对接触力的影响Fig. 14 Influence of object radius on contact force whenT1=1N·m
2.3.3 指骨角度的限制
指骨旋转角θ1和θ2必须具有最小的开口角(θ1o,θ2o)才能抓住最大的物体,必须有最大的闭合角(θ1c,θ2c)才能抓住最小的物体.
在 robj=53.75mm 时计算全开口最小角度,此情况适合 3点抓握.利用式(1)、(2)、(11)计算θ1o可得θ1o<0.7314rad.考虑一个裕度,取θ1o=π/4. θ2o必须确保让物体进入机械手,所以θ1o+θ2o≤π/2,θ2o≤π/4.
取θ2o=π/4,使得当机械手完全打开时远端指骨平行并避免物体在关闭之前被弹出.为了计算最小闭合角,考虑了直径为25mm的物体.由式(1)和(2)得:θ1c>1.760rad,θ2c>1.760rad,故取θ1c=θ2c=2rad.
为了避免可能的碰撞,必须满足以下等式:L1s inθ1c+ L2sin(θ1c+θ2c)>t,10.95mm>t=9mm.
当手指完全闭合时,远端指骨和手掌之间没有发生碰撞.
2.3.4 接触力计算
机械手的力由Dynamixel MX64AT伺服电机提供.该电机可提供高达 7.3N·m 的扭矩.使用直径10mm 的滑轮,初级肌腱的张力可达 1460N.这意味着手指的驱动力有365N.如2.3.3节所述,最关键的是抓取目标最大尺寸时.由式(8)、(9)、(10)计算接触力,其 Matlab模拟结果如图 15所示,在最坏的情况下(robj=50mm ),4个远端指骨最大力约为67N,掌心力约为61N.
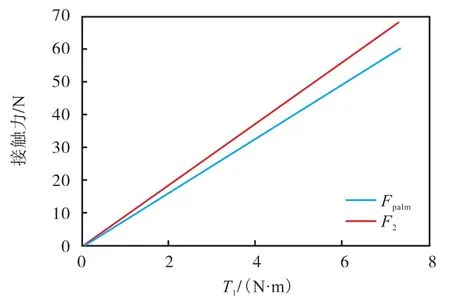
图15 T1对接触力的影响Fig. 15 Influence of T1 on contact force
3 手指滑轮的优化
手指滑轮负责将肌腱的张力传递给指骨使其闭合.如果滑轮设计不当,将导致内部产生巨大张力.为了承受这些力,手指需要更大更重[10].
为了得到更大的力矩,同时减小张力,需对欠驱动手指上主滑轮和副滑轮位置进行分析,故独立出一个指节对其进行分析.
Ge是张力σ在角平分线上的分力,G 是与两滑轮中心连线c垂直的力,两者夹角为β.

几何关系为
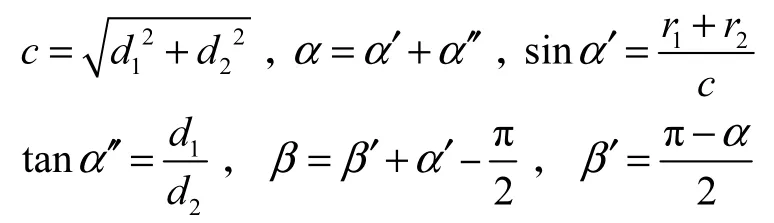
分析图 16 得到以下结论:(1)二级滑轮半径越小,指骨产生的扭矩越大;(2)使主滑轮和二级滑轮相切,使二级滑轮的进、出口平行,此时Ge可以达到最大值.
但二级滑轮的半径不可能为 0,因为这会增大摩擦导致切断肌腱.同时,不可能使主滑轮和二级滑轮相切,因为这样会引起它们之间的摩擦.另外,可以设计二级滑轮的进、出口,但这需要更多的滑轮,会增加机械手的质量和肌腱的摩擦.
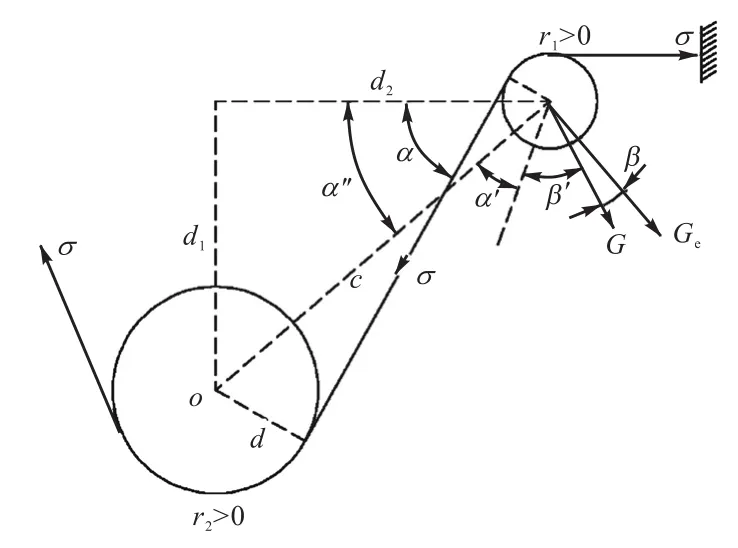
图16 滑轮组结构分析Fig. 16 Pulley structure analysis
综上,这些指导方案虽不能实现,但必须尽可能多地遵循,以尽量减少指骨的内力.
主滑轮的位置和半径都已经在2.3节确定,主滑轮半径是由近端指骨的扭矩和传动比的最大值所决定的.因此,还需要确定的参数是二级滑轮的半径和位置.
首先确定二级滑轮的最小可能半径.这个半径受到了肌腱和滑轮阻力的限制.由于没有足够的空间来使用旋转滑轮,所以决定使用钢条作为二级滑轮.这增加了二级滑轮和肌腱之间的力,但它允许设置一个更小的滑轮.选用半径为 1.5mm的杆作为二级滑轮,并验证了摩擦张力损失是可以接受的.更小的半径会损伤肌腱,导致更大的摩擦损失.
手指滑轮系统设计如图 17所示,为了使主滑轮和二级滑轮尽可能的相切,故需要对主滑轮和二级滑轮之间的最小距离进行测试.
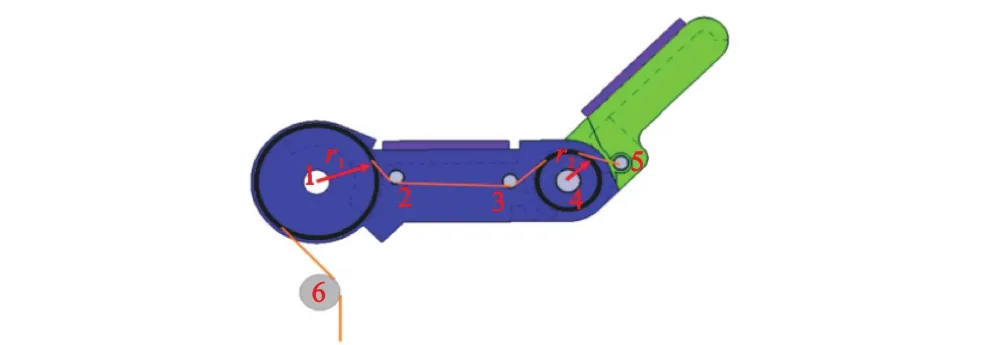
图17 手指滑轮系统设计Fig. 17 Design of finger pulley system
将近端指骨的二级滑轮(2)与主滑轮(1)的外径相切,此时圆心距为13.5mm,但摩擦过大,故须增大圆心距;当距离增加到 16.5mm 时,肌腱的滑动会更好.因为最大的摩擦损失都来源于主滑轮与肌腱之间的接触,所以将滑轮尽可能靠近手指的上半部分,以减小主滑轮与肌腱之间的接触长度.同样,远端指骨二级滑轮(5)的位置也应尽可能地与远端指骨主滑轮(4)相切,但远端指骨主滑轮的外径会限制它的位置,如图 18所示.为引导肌腱到远端指骨的主滑轮(4),故需要在(2)和(4)之间增加辅助滑轮(3).欠驱动3D打印机械手的实物图如图19所示.

图18 近端指骨的二级滑轮位置和远端指骨二级滑轮位置Fig. 18 Secondary pulley position of proximal phalanx and distal phalanx

图19 机械手实物图Fig. 19 Hand physical image
4 结 语
本文以欠驱动原理为基础,利用3D打印技术,制作了一种廉价、轻巧、便于更换零件的欠驱动机械手.介绍了欠驱动原理及特点,重点分析了抓握类型以及各抓握类型的边界条件,计算机械手尺寸和驱动参数,优化机械手手指机构.最终实现稳定抓取直径为 25~100mm 的圆柱形物体或具有相同尺寸的非圆柱形物体的功能,这使得机械手能够适应不同形状的物体.

