Lane-Emden型微分方程数值解的Euler小波方法

徐志刚，周凤英

(东华理工大学 理学院, 江西 南昌 330013)

Lane-Emden方程是与二阶常微分方程有关的奇异初边值问题，被用来模拟数学物理学和天体物理学中的如热爆炸、球形气体云的热行为和热离子流等现象[1-2]，此方程因由2位天体物理学家Lane和Emden共同研究而命名.带形状因子α的Lane-Emden方程[3-5]具体形式如下

(1)

考虑如下3种边界约束条件：

Dirichlet边界条件：

y(0)=α1，y(1)=β1；

(2)

Neumann边界条件：

y′(0)=α2，y′(1)=β2；

(3)

Neumann-Robin边界条件：

y′(0)=0,α3y(1)+β3y′(1)=γ3，

(4)

其中，αi,βi,i=1,2,3和γ3为常数,f(x,y)满足Lipschitz条件.

数值求解Lane-Emden方程的主要困难是x=0处的奇异性.已有学者提出了一些方法来求解带有Dirichlet和Neumann-Robin型的Lane-Emden方程，如配点法[6-7]、有限差分法[8]、样条有限差分法[9]、B-样条[10]、三次样条方法[11]、Adomian分解方法[12]、变分迭代法[13-14]、同伦分析法[15]和小波方法[15]等，但对于具有Neumann型边界条件的Lane-Emden方程数值方法的文献鲜有.

近年来，由于小波所具有的紧支撑性、消失矩、正交性等特点，基于小波的数值技术已在数值逼近领域守到广泛关注.其中由多项式经过伸缩、平移生成的小波被用于解决不同类型的线性和非线性(分数阶)常微分方程和偏微分方程，如Legendre小波[16]、Chebyshev小波[17]和Bernoulli小波[18].最近，Euler小波[19]首次提出并应用于非线性Volterra分数阶积分微分方程数值求解.目前关于Euler小波的文献很少，尚未有文献将其应用到Lane-Emden方程的求解.为了进一步推广Euler小波的应用，笔者利用Euler小波配置法求解具有Dirichlet，Neumann和Neumann-Robin类型边界条件的Lane-Emden方程.小波的应用主要是通过小波积分算子矩阵和微分算子矩阵将所求方程转化为代数方程组进行求解.现有Euler小波文献[19-20]借助Block函数构造了Euler小波函数的分数阶积分算子矩阵，与文献方法不同的是，笔者不使用积分算子矩阵，而是借助推导的Euler小波函数任意分数阶积分计算公式将所求方程转化为代数方程组进行求解，然后应用牛顿迭代法进行数值求解.数值实验结果表明本文方法的有效性.

1 Euler小波函数及收敛性分析

1.1 Euler小波函数定义[19]定义在[0,1)区间上的Euler小波共有4个参数，k是任意正整数，n=1,2,3,…,2k-1,m为Euler多项式的阶数，x为自变量，Euler小波定义如下

(5)

(6)

若将式(6)中的无穷级数截断，则式(6)能写成

其中，C和Ψ(x)是矩阵，由如下给出

C=[c10,c11,…,c1,M-1,c20,…,c2,M-1，…,c2k-1,M-1]T，

(7)

Ψ=[ψ10,ψ11,…,ψ1,M-1,…,ψ2k-1,M-1,…,ψ2k-1,M-1]T.

(8)

1.2 Euler小波收敛性

2 Euler小波函数任意分数阶积分公式推导

将推导Euler小波函数在如下Riemann-Liouville分数阶积分定义下积分计算公式

(9)

定理2定义在区间[0, 1)上的Euler小波函数ψn,m(x)的任意α>0阶积分计算公式如下给出

(10)

(11)

(12)

定理2得证.

3 算法描述

给出在3种不同边界条件下求解Lane-Emden方程的Euler小波配置方法，为叙述方便，记Euler小波函数列(8)的α阶分数阶积分为IαΨ(x).

3.1 Dirichlet 型边界条件首先设方程(1)中未知函数的二阶导数可由Euler小波函数表示即

y″(x)=CTΨ(x)，

(13)

对方程(13)从0到x分别进行2次积分并结合边界条件(2)，可得

y′(x)=(β1-α1-CTI2Ψ(1))+CTIΨ(x)，

(14)

y(x)=α1+x(β1-α1-CTI2Ψ(1))+CTI2Ψ(x)，

(15)

将式(13)、(14)和(15)代入方程(1)，得

(16)

3.2 Neumann 型边界条件设方程(1)中未知函数y(x)的二阶导数可由Euler小波函数表示即

y″(x)=CTΨ(x)，

(17)

对方程(17)从0到x分别进行2次积分并结合边界条件，可得

y′(x)=α2+CTIΨ(x)，

(18)

y(x)=xα2+y(0)+CTI2Ψ(x)，

(19)

将y(0)看作未知变量，并将式(17)、(18)和(19)代入方程(1)，得

(20)

由边界条件(3)，得

α2+CTIΨ(1)=β2.

(21)

3.3 Neumann-Robin 型边界条件设方程(1)中未知函数y(x)的二阶导数可由Euler小波函数表示即

y″(x)=CTΨ(x)，

(22)

对方程(22)从0到x分别进行2次积分并结合边界条件，可得

y′(x)=CTIΨ(x)，

(23)

y(x)=y(0)+CTI2Ψ(x)，

(24)

将y(0)看作未知变量，由边界条件(4)，结合式(23)和(24)可得

(25)

并将表达式(22)、(23)、(24)代入方程(1)，得

(26)

4 数值算例

例1 考虑如下带有 Dirichlet边界条件的Lane-Emden方程

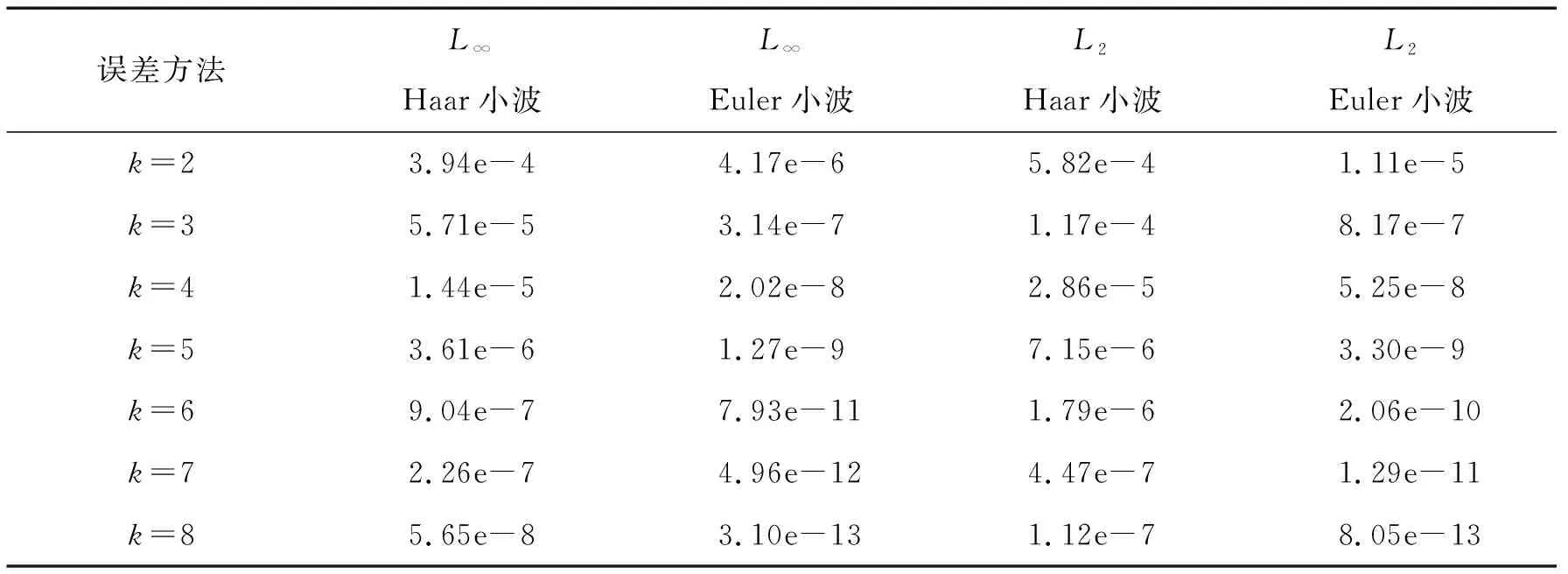
y(0)=ln 2，y(1)=0 0

表1给出了Haar小波[4]与本文算法的L∞和L2误差.从表1可以看出，固定M=4的值，通过提高Euler小波的分辨率尺度k产生稳定的收敛解.表 2给出了Euler小波在不同参数情况下的L∞误差.从表2知，固定Euler小波的分辨率尺度，提高M值，可以得到更高精度的数值解，这也与定理1的结论一致.表3给出了不同参数情况下的数值解与精确解的比较.

表 1 不同参数情况下的L∞与L2误差比较

表2 不同参数情况下的L∞误差

表3 不同参数情况下的数值解与精确解的比较

例2 考虑如下带有 Neumann边界条件的Lane-Emden方程

表4给出了Haar小波[4]与本文算法的L∞和L2误差.从表4可以看出，固定M=4的值，提高Euler小波的分辨率尺度k产生稳定的收敛解.表 5给出了Euler小波在不同参数情况下的L∞误差.从表5知，固定Euler小波分辨率尺度而提高M值，可以得到更高精度的数值解.

表 4 不同参数情况下的L∞与L2误差比较

表5 不同参数情况下的L∞误差

例3 考虑如下带有Neumann-Robin边界条件的Lane-Emden方程

表6中给出了Haar小波[4]的L∞和L2误差.从表6可以看出，固定M=4的值,提高Euler小波的分辨率尺度k产生稳定的收敛解.表 7给出了Euler小波在不同参数情况下的L∞误差. 从表7知，固定Euler小波的分辨率尺度而提高值M，可以得到更高精度的数值解.

表6 不同参数情况下的L∞与L2误差

表7 不同参数情况下的L∞误差

5 小 结

提出了一种求解非线性奇异Lane-Emden方程数值解的 Euler小波法.利用Euler多项式的解析形式，在Riemann-Liouville分数阶积分定义下，推导了Euler小波函数的一般分数阶积分计算公式.利用所推导的公式结合配置法将Lane-Emden方程求解转化为一组非线性代数方程，然后应用牛顿迭代法进行求解.通过数值算例与相关文献及精确解进行比较，验证了该方法的有效性和适用性.该算法编程简单、有效，使用非常小的和值就能得到高精度的近似解.