应用图像块的运动模糊图像盲恢复算法

郭立文，廖永忠

1(陕西国防工业职业技术学院 计算机与软件学院，西安 710300) 2(湖南第一师范学院 信息科学与工程学院，长沙 410205)

1 引 言

成像过程中的相机晃动是图像模糊的一个重要成因，去除这种运动模糊是图像去模糊研究的一个重要研究方向，图像去模糊过程本质是对一类病态的反卷积方程的求解，如何高效、准确的求解此类方程是图像去模糊研究的难点问题.

图像的盲去模糊是指在图像的模糊核函数未知情况下的图像去模糊方法，盲去模糊算法是当前图像恢复研究十分活跃的一个领域，一些学者在近几年取得很多高水平的研究成果，相关的期刊和会议上有很多此类研究的文章[1-4].MIT的Levin提出一种基于边缘概率密度函数的模糊核估计算法[5]，用高斯混合分布模型表示自然图像的先验分布，然后采用期望最大化(EM)算法交替迭代实现模糊图像的恢复.Taeg Sang Cho在文献[6]中利用图像直线边缘在模糊过程中发生变化，其Radon变换与模糊核函数之间有确定的对应关系，从而确定模糊核函数的方法，然后用最大后验概率(MAP)完成模糊图像的恢复.Bae H提出一种快速的模糊图像恢复算法[7]，其认为由于自然图像梯度的稀疏分布特性，图像模糊信息都包含在图像的边界中，对图像进行分块，然后提取一些包含较多信息边界的块，再把它们进行拼接，利用这个模糊图像块完成模糊核的估计，该算法能降低计算量.Lin Zhong 提出强噪声下大尺寸模糊核的图像去模糊图像算法，先利用方向滤波去噪，然后Radon变换重构模糊核函数[8].文献[9]以多组代价函数的优化为目标，实现图像去模糊效果且极大的提高了算法的实时性.与此同时基于传统的参数估计的图像盲去模糊算法也被提出[10，11].

这些算法的计算量十分巨大，且对计算机内存要求很高.本文提出了一种新的交替快速迭代算法，能极大的提高图像去模糊的速度，使得图像盲去模糊算法的实时实现成为可能.

2 原理与模型

2.1 图像模糊方程

一般来说，运动模糊图像的数学模型为：

g(x，y)=f(x，y)⊗h(x，y)+n(x，y)

(1)

式中g(x，y)表示降晰后的模糊图像，f(x，y)表示降晰前的清晰图像，h(x，y)为模糊核函数(PSF)，n(x，y)一般假定为零均值的高斯噪声.

2.2 Radon变换

对一个二维图像f(x，y)，其Radon变换可以看成图像f(x，y)沿与某一直线的一维投影，或者说是图像f(x，y)定义在与某一直线的线积分.所以f(x，y)的Radon变换数学表达式为[12]：

(2)

式中的直线l的方程为：b-xcosθ-ysinθ=0，利用冲激函数δ(·)的特性，Radon变换的数学表达式可以写成如下表达式：

(3)

式中b表示直线l到坐标原点的距离.

3 模糊核的估计

经验告诉我们，如果一幅自然图像中有直线轮廓，模糊后的结果是直线轮廓边缘会发生明显的变化，产生毛边，即边缘的模糊，而这些边缘的模糊与模糊核函数是有直接关系，这里通过利用图像边缘的模糊方程来推导其与模糊核函数之间的关系.

3.1 模糊核与模糊直线边缘关系

前面已经定义了一个二维图像f(x，y)的Radon变换，如式(3)所示，根据二维函数的卷积定义，不考虑噪声的影响，模糊图像的卷积方程写成积分方程的形式为：

(4)

假设二维图像f(x，y)是一个理想的直线，其与x轴夹角为θ′，且θ′=θ+π/2，直线方程可以写成如下表达式：

f(x，y)=δ(xsinθ′-ycosθ′)

(5)

又因为f(x1-x，y1-y)是f(x，y)的线性变换，所以也是直线，用冲激函数表达此直线为：

(6)

对于一个理想直线图像，模糊后所得到的模糊图像假设为gL(x，y)，其表达式可以重新写为：

(7)

代入θ′=θ+π/2，有：

(8)

根据Radon变换定义，有：

(9)

gL(x1，y1)=Rh(ρxy，θ)

(10)

由此可见，当f(x，y)是一个理想直线轮廓时，模糊后的直线法向截面轮廓等于模糊核函数的Radon变换，这给我们提供了一个思路，如果找到一幅图像中的模糊直线边缘，就可以通过求解反Radon变换来确定模糊核函数.

3.2 模糊核实验测试

这里选用了文献[5]的一个模糊核函数，如图1所示，其与一个只包含一条理想直线轮廓(不同角度)的黑白图像互相卷积来进行实验，对比结果如图2所示.

图1 测试用模糊核函数Fig.1 Kernel of testing

图2 测试结果Fig.2 Result of testing

3.3 模糊核的估计与图像的恢复

为简化起见，这里分别用f，g，h表示f(x，y)，g(x，y)，h(x，y)，根据图像的贝叶斯恢复理论有：p(f，h|g)∝p(g|f，h)p(f)p(h)，对每一个像素来说，模糊图像的梯度值和清晰图像的梯度值是相近的，这里假定其差值服从均值为零，方差为σ2的高斯分布[13]，故有：

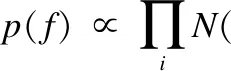
(11)

考虑已知f，h后，一方面，模糊图像g的分布由噪声n分布规律来决定，一般假定噪声为零均值的高斯分布，用pg表示，另一方面，为引入正则项，限制解的范围，引入一个新的条件，前面已经推导模糊图像的边界与模糊核函数的Radon变换相等，这里定义为：

p(g|f，h)∝pg(g|f，h)*pe(g|f，h)

(12)

假定图像噪声为零均值的高斯噪声，有：

(13)

(14)

定义代价函数：

E(f，h)=-log(p(f，h|g))

(15)

为简化计算，加快计算速度，取p(h)为高斯分布，有：

E(f，h)=λ1‖f⊗h-g‖2+λ2‖f-g‖2+
λ3‖h‖2+λ4∑q‖gLθq-Rθqh‖2

(16)

图像的去模糊过程转变为这个方程的优化求解，交替优化这个代价函数就能得到模糊核函数和清晰图像.

优化这类代价函数，采用交替迭代的算法，分为两步，第一步，固定h，求解f：

(17)

式(17)包含两个二次项，利用傅里叶变换快速求解：

(18)

第二步，固定f，求解h：

(19)

方程的三项都是二次项，但是第三项包含有Radon变换，采用了共轭梯度法进行优化求解：

(20)

式中粗体分别表示相应的算子矩阵，可得方程的解为：

(21)

4 图像块的处理与图像块的选择

4.1 引导滤波

图像滤波是为了去噪，由于本算法利用直线边缘来估计模糊核，即模糊核函数只与图像直线边缘附近像素的变化有关，因此希望直线边缘附近图像在去噪同时又能保持图像边缘.一些简单的去噪方法会导致图像直线边缘发生变异，变得更加模糊，破坏了直线边缘所携带的原始信息，因此，需要选择合适的滤波算子，在实现图像去噪的同时，进一步平滑光滑区域部分的图像，保持直线边缘附近的图像信息，这里采用引导滤波来去噪.

引导滤波是近些年提出的图像滤波方法[14]，其核心思想是假设该输出图像与引导图像(或是输入图像)在一个二维图像窗口wk内满足线性关系.

qi=akIi+bk，∀i∈wk

(22)

式中，qi是输出图像，Ii是输入图像，i和k是索引，在窗口wk内，一般假定ak和bk是常数.对上式两边取梯度有：qi=akIi，这表明其梯度特性没有发生变化，边缘细节保持不变.设输入图像pi，通过让输入图像和输出滤波图像的差值最小来确定两个参数akbk的值，如下式所示：

(23)

(24)

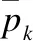
直接采用输入滤波图像作为引导图像的时候，即Ii=pi，如果=0，则是式(6)的解，输出等于输入，引导滤波器无效.如果>0，在图像平滑的区域，ak的值较小或等于0，而bk的值近似于等于此时引导滤波器为加权均值滤波器；而在图像边缘特征比较丰富的图像区域，ak近似于1，bk近似于0，引导滤波器也基本无效，从而保持原来图像边缘的基本特性.故引导滤波器的滤波效果在窗口尺寸固定的情况下，基本是由参数确定.引导滤波另外一个更重要的特性是其计算时间复杂度，引导滤波的时间复杂度为O(No)(No为待处理图像的像素数目).图3为对LENA图像加噪后，分别用双边滤波和引导滤波去噪后效果图像.

图3 图像去噪Fig.3 Image denoising

4.2 图像块的选择与提取

实验中发现，由于不同图像的尺寸大小的差异，以及不同图像所包含的直线轮廓数量也各不相同，故而算法的计算时间和内存消耗相差悬殊，特别是在图像尺寸较大的情况下，计算机内存不足和计算时间过长的问题特别突出.我们已经知道图像的直线轮廓像素数目在整幅图像中是一个较小的值，这启发我们可以通过提取图像主要轮廓边界，降低图像尺寸来完成模糊核的估计，实现模糊图像的恢复.

图像的模糊核函数依赖于图像中直线轮廓法向截面轮廓的反Radon变换，而反Radon变换的知识告诉我们，获得在不同角度下图像Radon变换的向量越多，提供的信息量就越大，使用最大后验概率的获得精确解的概率就越大.

因此，本文首先对图像进行分块，然后找到包含不同角度最多直线边界的几个块进行拼合(本文选用4个)，拼合时候要考虑模糊核尺寸的大小，利用掩膜消除块边界的影响，然后利用拼合的图像完成模糊核函数的重构，从而降低计算量和减少内存的消耗.图4为对一幅图像采用本方法先分块，然后选择合适的图像块，最后进行拼合后的结果.

图4 图像块选择Fig.4 Image patch choosing

这里采用了文献[6]方法检测边界，因为直线轮廓的法向截面轮廓与模糊核函数的Radon变换相等，需要对提取的直线轮廓进行筛选，选择在直线边界附近没有其他轮廓干扰的直线边界作为候选边界.

5 图像恢复

5.1 合成模糊图像的实验结果

这里选用三幅自然图像作为测试图像，如图5所示，从文献[5]选择三个模糊核函数作测试，如图6所示，其相互卷积加2%的高斯白噪声，得到9幅含噪的模糊图像，分别采用本文的算法与文献[6]的最大后验概率法(MAP Radon)，进行对比试验(计算机配置CPU为3.1GHz，内存为10GB，软件MATLAB2012a)，实验的结果如表1所示.从表可知，本文算法的计算时间和PSNR值均优于MAP Radon算法，同时，本文算法克服了MAP Radon算法占用内存大的缺点.

图5 测试用图像Fig.5 Image of testing

图6 测试用模糊核函数Fig.6 Kernel of testing

表1 与算法比较PSNR值(db)和计算时间(s)Table 1 Comparison of PSNR values and the computation times

图7 去模糊结果Fig.7 Image deblurring results

5.2 实际自然模糊图像恢复

分别选用文献[6]提供的测试图像和文献[15]提供的一副测试图像进行实验，实验的结果如图7所示，计算时间如表2所示，从表中可见，本文算法的时间是远远小于MAPRadon算法，且在运行过程中，不会出现该算法最常见的内存不够的现象，在图像的恢复质量上，本文算法恢复的图像，在视觉上的恢复效果丝毫不逊色于对比算法所获得的恢复效果，在一些细节上，本文算法更具有优势.

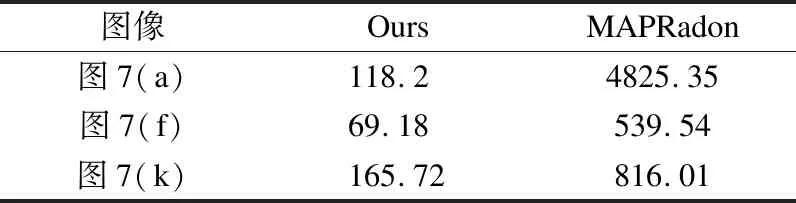
表2 计算时间对比Table 2 Comparison of the computation time(s)

6 结 论

本文提出一种基于图像信息块的单幅模糊图像盲恢复算法，通过检测图像的直线边界，在图像中找出包含最多信息边界的图像块进行拼接，以此拼接图像来估计模糊核函数，完成模糊图像的盲恢复.实验结果证明，相对于MAPRadon算法，本文算法在不损失恢复图像质量的前提下，明显提高了计算速度并降低了内存的占用量，降低了计算的时间和对硬件的要求.