竖向简谐振动下群桩分析

宗传书 刘丽华

摘 要：提出一种竖向荷载作用下群桩简化分析法，该方法利用 Kausel和Roesset提出的刚度矩阵模拟桩周土层的动反应。该方法的优点是可以通过自由场土位移和桩土接触力的计算，利用单桩的计算结果进行群桩分析，但是必须考虑桩周土的作用。通过与现存其它计算理论解得比较，验证了该计算方法的可行性。

关键词：桩群;竖向荷载;动力分析

本文提出了一种进行桩在竖向简谐荷载作用下小应变分析法，利用 Kausel和Roesset提出的刚度矩阵模拟桩周土层的动反应，从而可以有效考虑桩周土层对桩的影响。该方法假定土为线性、桩土完全接触无滑移现象、不考虑水平位移。另外对土的弹性矩阵进行近似简化，可以由单桩的动反应来进行桩群的分析，这种方法在桩数量特别多时比其他现存的方法更方便、适用。

一、分析模型

（一）单桩分析

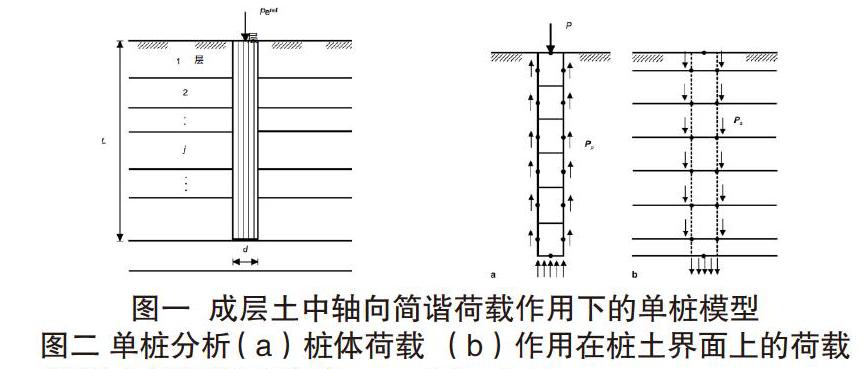
单桩计算模型如图一所示。每层土均为弹性材料，杨氏模量E_s，泊松比V_s，质量密度ρ_s;桩为弹性柱体，长度为L，直径d，横截面积A_s，杨氏模量E_p，密度ρ_p。桩土受力如图二所示，桩体受竖向荷载和桩土相互作用力作用，土体仅受相互作用力作用，桩视为一维有限单元体，土为水平成层连续体，在桩土界面上，作用力保持平衡，单桩平衡方程为（K_p-ω²M_p）w_p=P+P_p（1）

其中ω为振动频率，w_p为桩竖向位移矢量，P_p为作用在桩上的桩土相互作用力矢量，P为作用在桩顶的外部荷载矢量，K_p和M_p为桩的刚度矩阵和质量矩阵。

图一  成层土中轴向简谐荷载作用下的单桩模型

图二 单桩分析 （a）桩体荷载   （b）作用在桩土界面上的荷载

桩周土的平衡方程为：w_s=F_sP_s（2）

其中F_s为土的挠度矩阵，P_s为作用在土上的桩土相互作用力，w_s为土层的竖向位移矢量。由于桩土接触面桩土相互作用力平衡以及位移协调，方程1变为（K_p+F_s^-1-ω²M_p）w_p=P（3）

其中F_s^-1是F_s的逆，w_p为未知量，一旦确定w_p，则可通过轴力与桩端竖向位移的比值确定桩的阻抗。利用 Kausel和Roesset提出的刚度矩阵计算挠度矩阵F_s，对于成层土，将每层土叠加得整个桩周土的平衡方程：KU=S（4）

其中K为土层整体刚度矩阵，U为土层位移矢量，S为作用在土层上的外荷载矢量。这种方法首先要求荷载按照Hankel变换以谐波分量形式增大，從而可以得到土层的传递位移，该方法将三维问题简化为一维问题，计算简单，并且一旦确定所有谐波分量的传递位移，则在指定深度，土层的实际位移函数可以用Hankel逆变换得出   （5）

其中r为自桩轴线算起的径向横坐标，u（r）为指定深度处传递位移，J₀（kr）为零阶一类贝塞耳函数。

（二）群桩分析

对于群桩，通过每颗桩力的平衡和接触面位移协调，其动力平衡方程为K_PG+F_sG^-1-ω²M_PG）w_PG=P_G（6）

其中K_PG和M_PG分别为群桩刚度矩阵和质量矩阵，W_PG为桩的节点位移矢量，P_G为桩顶荷载矢量，F_sG为土的挠度矩阵F_sG的逆，它可以利用前面单桩分析时的过程计算，一般假定桩周为自由场，为简化计算，假定所有桩均相同，则方程6便变为m×n个方程，m为桩数，n为每颗桩的节点数，未知量为节点位移和桩端荷载，因此计算中必须考慮桩帽的作用，在本文中，仅考虑桩帽为刚性或完全弹性的情况。当桩帽为完全弹性时，桩端荷载已知，则利用方程6可直接计算出节点位移矢W_PG;当桩帽为刚性时，由于桩帽和桩端完全接触，所以两者位移保持协调。

当桩群中桩数特别多时，这种计算方法计算比较繁琐，为简化计算，本文提出了一种更实用的方法。将方程（2）扩展到群桩，即

（7）

其中W_si为桩i与土接触面上土的竖向位移，P_si和P_sj为作用在桩i、j 周土上的作用力矢量，F_s为单桩挠度矩阵，△F_sij为桩j对桩I 的附加挠度矩阵，利用方程5 可以计算桩i 任何节点的实际位移，为简化计算，假定每根桩的作用力相同，即P_si=P_sj，则由方程7可以得出桩i的挠度矩阵为

（8）

方程8对于成轴对称分布的桩群或仅有2-4颗桩组成的桩群来说是准确解，在其他情况下，例如当桩直径不同或桩距非常小时，它仅是近似解。但是通过与准确解和现场测量值比较，当低频振动时，这种近似解是可以接受的。同方程3类似，主动桩i的控制方程为

（9）

其中w_Pi、P_i分别为桩i的位移矢量和作用在桩i节点上的外部荷载。将方程9扩展到桩群中的每颗桩，可得到桩群的一系列方程，这些方程的解比用方程6得出的解简单，但是它不考虑桩帽的质量，并且假设桩群的竖向动阻尼是振动频率的函数。此函数确定后，质量为M_c的桩帽竖向位移为：

（10）

其中桩帽的竖向位移，F_z为桩帽荷载，K_z为竖向阻抗。

二、方法验证

当桩数特别多时，方程9可以节约计算量和时间，比较适用于成层土中大的桩群的计算分析。本文我们把基于方程6和9的解分别称为完全解和近似解，并在图三中将这两种解与其它方法的结果作了比较，验证了其正确性。表中3×3桩群阻抗的实部K_r、虚I_m绘制成无量纲频率的函数，其中V_s为土的剪切波速。为便于作图，以K_r/9K_st和I_m/9K_st为纵坐标，其中9为桩数K_st为单桩静刚度。本例中桩群处于各向同性半空间中间距为2d并假定桩帽与桩刚性连接不与土层接触。分析中用到的其它数据为：E_p/E_s=1000，L/d=15，，，。

三、 结束语

提出一种竖向荷载作用下群桩简化分析法，该方法利用 Kausel和Roesset提出的刚度矩阵模拟桩周土层的动反应，特别地提出了一种计算成层土中较大桩群的近似计算法，该方法方便实用、节约计算量和计算时间，与其他计算方法的比较验证了其可行性，为桩基的动力研究奠定基础。

参考文献：

[1]刘晶波，杜修力.结构动力学[M].北京：机械工业出版社，2005

[2]宰金珉，宰金璋.高层建筑基础分析与设计[M].北京：中国建筑工业出版社， 1993， 53～62.